如何突破排列组合应用题的难点

张 辉

解决排列组合应用问题需要有较强的问题分析能力,要求学生能够将实际问题合理地转化为使用分类加法计数原理与分步乘法计数原理求解的问题. 同时需要具有严谨、缜密的思维,分类要不重不漏,分步要连续完整. 解决排列组合问题最重要的是要分清楚是排列问题还是组合问题,从而确定一个事件是分步完成还是要将其分为几类讨论. 在分类时,若不符合条件的数值较易计算,也可以从所有可能的排列组合数中减去不符合条件的排列组合数得出结果. 本文谈谈如何突破解决这部分问题时遇到的难点.

1 选择“特殊元素”还是“特殊位置”

在解决排列组合问题时,一定要抓住问题的特点,分析出“元素”与“位置”的关系加以解决.

例18名毕业的学生在母校合照留念, 8人排成前、后两排,每排4人. 3名女生中的2名要在前排,另外1名大个子的女班长要在后排,共有多少种排法？

（44）即日謹齋法信，叩頭恭詣龍虎山嗣漢天師門下。（《太上玄天真武無上將軍籙》，《中华道藏》30/584）

式中：C为对照值，T为处理值。当RI>0时，表示促进作用，当RI<0 时，表示抑制作用：RI绝对值的大小代表化感作用强度。

点评 本题是属于有限制条件的排列问题. 要完成的事件需要分步完成,所以会考虑起始步骤和各步的顺序,从而会出现多种解法. 解法1、解法2是从元素出发考虑解的过程;解法3、解法4是从位置出发来考虑过程(其中有先确定前排元素还是先确定后排元素之分). 所以,分步完成排列组合问题时,最关键的是步骤设计. 一般常采用如下方法:1)先考虑特殊元素;2)先考虑特殊位置;3)先确定元素的组合,再进行排列;4)先确定位置的组合,再进行排列.

例24位学生和2位老师共6人站成一排照相.

(1)有多少种不同站法?

(2)2位老师站在中间有多少种站法?

(3)A学生站在最左端有多少种站法?

(4)2位老师必须站在两边有多少种站法?

(5)2位老师中间有且只有1位学生有多少种站法?

(6)学生A，B必须站在一起(相邻)有多少种站法?

(3)分为3堆,1堆1本,1堆2本,1堆3本;

(7)2位老师相邻且站在边上有多少种站法?

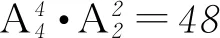
图1

A

图2

图3

(4)强钠长石化伟晶岩(图4)：灰白色，细粒花岗伟晶结构，交代结构，块状构造。主要矿物有钠长石、石英、白云母、电气石。其中钠长石约占65%，石英约占25%，白云母占5%～8%，电气石占2%～5%。钠长石、石英呈半自形-他形细粒，粒度小于10mm；白云母呈小片状，片径为10～15mm；电气石呈黑色柱状，大小(2～3)mm×(6～10)mm。岩石风化较强，呈砂糖状。

老师学生老师

图4

图5

点评 通过例2我们再次体会到对于含有附加条件的排列组合问题,要“一元素,二位置”，采用优先原则;另外要考虑每一个事件是“分情况完成”还是“分步骤完成”,从而来决定是采用加法原理还是乘法原理.

成立25年以来，国望集团现在上海、广东分别拥有4家子公司，在全国设有100多个服务网点，在全球设有50多个代理商。不论是与客户、代理商，还是与其他设备供应商的接触，每一次合作，都有值得国望集团珍惜的点滴，亦能挖掘出促进其再向前的力量。其中，与德国Baumann集团、日本小森的分别合作，更让其通过吸收融合而实现了技术上的不断提升。

2 采用“直接法”还是“间接法”

直接法就是从题设条件出发,直接求出符合条件的答案的方法;间接法就是从所有的排列数(组合数)里面减去不符合条件的排列数(组合数),从而间接地求出符合条件的排列数(组合数).

玉米倒伏病害的防治除了合理种植，还要根据不同玉米品种的差别安排玉米种植密度，同时也要注意钾、氮及磷肥的合理使用，根据当地土地的情况进行适当的补给。此外，为了预防在玉米拔节后氮肥量施加过多，可以将其分为苗期、穗期2次追肥。通过在玉米拔节后期采取一定措施可以有效防治玉米倒伏，在玉米拔节后期也要注意中耕培土的实施，促进玉米根部发育，从而提升玉米植株抗倒伏能力；在玉米拔节后期可以进行植物生长抑制剂的喷施，控制玉米植株高度。

基于无人船的水质监测技术，主要包括无人船自主航线规划及精准控制、多传感器集成与信息融合以及远程通信与实时多模控制，实现自动化、全天候、高精度水文监测，实时提取被测数据，借助云计算、大数据对特定时段水文情况进行分析。将该技术应用于水利环保等行业部门，可解决人工无法在恶劣天气或危险水域进行水样提取、水质监测等技术壁垒，覆盖全面范围水文监测的死角。

例34位学生和2位老师共6人站成一排照相,2位老师不相邻有多少种站法?

图6

如今，智慧宫与国内多家出版社合作翻译阿语图书，一年翻译数百本书，内容也由文学作品扩展到社会科学等方面。随着业务越做越大，主动上门来谈合作的境外文化机构也越来越多。白鑫和他的中国合伙人专门从阿拉伯国家邀请了50多名顶尖汉学家翻译中国图书，尽可能地保持著作的原汁原味。

例4从4名男生和5名女生中任意选出3人参加问卷调查,其中至少要有男生与女生各1人,则不同选取方法有( ).

A.140种 B. 84种 C. 70种 D. 35种

增加网站流量有妙招：图书馆在活动平台上抢当下热映的电影票的活动，就引起了读者的疯抢，为图书馆网站带来的大量流量，福建省图书馆通过在线抢票方式上线官网活动，活动平台的周点击率达到了13万人次。超过了一些门户网站一年的点击量。

例5用5个数字0,1,2,3,4组成没有重复数字的五位数,能够组成多少个比20 000大的数?

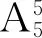
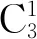
点评 解法1是根据题中限定的条件用间接法来求解;解法2、解法3是将问题分为若干步或者若干类来解决,是直接法. 从本题来看,间接法比较简便，通常当直接法需要讨论的情况比较多,尤其是解决含有“至多”“至少”这些条件的问题时,间接法更好用.

近年来，上海十院积极探索以“转型发展，病种结构调整”为导向的新医改形势下的医院成本核算体系建设，将成本控制与医院投入、医保支付、科室发展方向和资源规模、绩效工资总量核定等挂钩，深入分析服务于病人的医疗活动所产生的投入与产出、成本与绩效。聚焦临床技能、疑难复杂疾病诊治能力和科技创新的诊疗模式的效益分析和决策评价。努力抓住改革契机，引导医院统筹考虑政策目标和改革要求等因素，强化成本控制正向引导作用。深入调整医院业务收支结构，降低医院运行成本，严格控制不合理费用增长，主动适应新形势和新政策，激发财务管理的价值创造能力，积极推动医院转型发展。

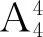
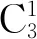
3 理解“平均分组”“不平均分组”以及“先分组再分配”

例66本不同的书,按照下列条件进行分配,各有多少种不同分法.

(1)分给甲、乙、丙3人,每人2本;

(2)分为3堆,每堆2本;

（2）配合使用高密度钻井液固相清洁剂降低固相含量，清洁钻井液。通过加入清洁剂，一方面可以降低钻井液中的无用固相，保证钻井液的清洁；另一方面可以有效抑制泥页岩地层水化膨胀分散，增强钻井液防塌抑制性和抗盐水污染能力［1］。

(4)分给甲、乙、丙3人,1人1本,1人2本,1人3本.

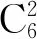
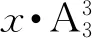
非物质文化遗产与景区、生活、产业、扶贫、文化、共享等相连接。新疆作为“一带一路”的必经之地，非物质文化遗产具有很大的附加值，我们不能简单地视之为旅游产品或纪念品，这也符合休闲旅游的体验化和参与性要求。基于此，我们可以从设计、生产、观摩、体验、网络营销、就地销售等各方面打造产业链条，形成一系列情境化、沉浸化、产业化、民俗化、娱乐化、大众化，以及有文化内涵、有传承意义的旅游产品。

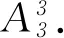
硫化氢在采场中的运移遵循流体动力弥散定律，由于硫化氢的浓度远低于其溶剂(空气)浓度，因此可以使用Fickian方法来描述物质传输中的扩散项。根据质量守恒定律和对流扩散方程得出硫化氢在采场中运移控制方程：

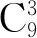
例75位大学生去3家单位实习,每家单位至少去1人,则不同的分配方法共有多少种?

你消费者不是讨厌商家挺着胸膛直着脖子扯着嗓子，大夸特夸自家所卖物品如何物美价廉超值享受嘛，好，听“上帝”的，咱不那样做，咱改弦更辙另辟蹊径，把昔日的自夸，转型、改版，升级为让顾客给产品找不足，指缺点，挑毛病。只要你“不足”找得对，“缺点”指得准，“毛病”挑得好，我们就感谢，就给予一定物质奖励。有的还从“挑刺儿”者中选出有代表性的人物，披红戴花，颁发证书，聘你为本厂本公司本商贸集团本行业的“产品质量社会监督员”。实践证明，这招儿很奏效：敢于“悬赏捉劣”，已经证明其商品过硬了，再加上对优秀“挑刺儿”“挑错”者的物质奖励和精神犒赏，双管齐下，广大消费者自然就会对该商品另眼相看，信任有加。

点评 例7是排列组合混合问题,解决此类问题一般先不考虑顺序,当组合问题来考虑,然后再考虑顺序,解决排列问题. 这种先分组再分配的方法较为简便，但需注意，若遇到平均分组,需要再除以排列的顺序数.

例8某学校派6名骨干教师去对口的甲、乙、丙3所学校支教,每所学校至少1人,其中王老师不去甲校的分配方案种数为________.

解析 此题既有分类的问题,又要考虑分组情况,还要注意分组分配时是否有序的问题. 6名教师到3所学校,每所学校至少1人,可能的分组情况为4,1,1;3,2,1;2,2,2.是分组以后再分配的问题.

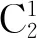
综上，有60+240+60=360种分配方案.

4 了解 “挡板法”与“插空法”的区别

例9有编号为1,2,3的3个盒子和10个相同的小球，将10小球全部装入3个盒子中,使得每个盒子所装球数不小于盒子的编号数,装法有多少种?

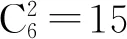
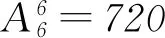
总之,在解决排列与组合应用问题时,常用下列几种方法：相邻问题捆绑法, 即在特定条件下,将几个相关元素视为一个元素来考虑,等整体排好后,再考虑它们“内部”排列;相间问题插空法,即先把一般元素排好,然后把特定元素插在它们之间或两端的空当中;特殊元素(位置)优先法,即优先考虑问题中的特殊元素或位置,然后再排列其他一般元素(位置);多元问题分类法,即将符合条件的排列分为几类,每一类的排列(组合)数比较容易求出,然后再求和;多步问题分步法,即完成一件事需要多步,每一步的排列或组合数比较容易求出,然后再求每一步排列或组合数的乘积.解决好排列组合应用问题,需要掌握一些典型问题的分析方法,上述方法是基本的,但不是固定的. 最重要的是要针对不同题设条件,分析清楚题目要做什么,用好分类加法计数原理与分步乘法计数原理,不能生搬硬套,要采用灵活的方法解决问题.