透析排列组合问题中的分配问题

徐艳敏

排列组合问题是高中数学计数的基本方法,也是学好概率的基础．分配问题是排列组合中的常考类型,处理此类问题时,需要将待分配的个体先分组,再分配．根据待分配的个体是否相同,又可分为不同元素的分配问题和相同元素的分配问题．本文结合例题说明这两类分配问题的求解策略，供同学们参考．

1 不同元素的分配问题

不同元素的分配问题,通常是先分组后分配,将n个不同名额,按一定的条件分成m组,根据所给的条件可分为平均分组、不平均分组、部分平均分组,分组的过程常借助分步计数原理及排列组合知识．分组时,若两个组中的个体数相同时,则两个组不进行区分．分配时根据所给的条件又可分为定向分配与不定项分配．两个单位中个体数相同,但分配的名额不同时,仍需区分．

例1(1)将6名实习生,分配到A，B，C三个工作单位,A单位1人,B单位2人,C单位3人,共有多少种分配方法？

(2)将6名实习生,分配到A，B，C三个工作单位,一个单位1人,一个单位2人,一个单位3人,共有多少种分配方法？

(3)将6名实习生,分配到A，B，C三个工作单位,每个单位2人,共有多少种分配方法？

(4)将6名实习生,全部分配到A，B，C三个工作单位，每个单位至少1人,共有多少种分配方法？

解析 (1)属于非平均分组,且为定向分配问题,即每个单位的实习生人数是确定的,故直接利用分步原理及组合知识进行分配即可．

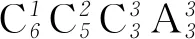
表1

(4) 每个单位至少1人,可能存在平均分组的情况,也可能存在非平均分组的情况,还可能出现部分平均分组的情况．

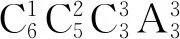
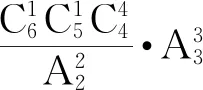
2 相同元素的分配问题

当某个待分配的单位要分得的名额至少为t(t>1)个时,可先分给其t-1个名额;没有要求某些待分配的单位至少分得1个名额时,可先向其借1个名额．进而将问题转化为每个单位至少分得1个名额的问题来求解．

例2(1)将8个评优名额,全部分配给A，B，C3个班,每班至少1个名额有多少种分配方法？

(2)将8个评优名额,全部分配给A，B，C3个班,每班至少2个名额,有多少种分配方法？

(3)将8个评优名额,全部分配给A，B，C3个班,有多少种分配方法？

(4)将8个评优名额,全部分配给A，B，C3个班,A班至少1个,B班至少2个,C班至少3个,共有多少种分配方法？

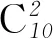
综上,处理分配问题时首先要明确是相同元素的分配,还是不同元素的分配；是平均分配还是非平均分配;是定向分配,还是非定向分配．准确利用相应模型的处理方法,以不变应万变．

链接练习

1. 某校从3名英语系、4名日语系和5名韩语系的学生中选5人组成一个语言交流小组,则英语系、日语系、韩语系都至少有1人的选择方法有________种.

2. 有5名学生报名参加“清华大学”“北京大学”“上海交通大学”3所高校的冬令营,每人限报1所学校,若每所学校的冬令营都至少有1名同学报考,那么这5名同学不同的报考方法共有( ).

A. 144种 B. 150种 C. 196种 D. 256种

3. 把编号为1,2,3,4的四个球放到编号为1,2,3,4的四个盒子中,每个盒子一个球,则球与盒子的编号不相同的方法有________种.

链接练习参考答案

1.590. 2. B. 3. 9.