例谈晶胞计算

闫翠红

由于晶体结构知识能全面考查学生的观察能力、思维能力和空间想象能力,在分析这类题目时,可让学生通过对晶体结构的观察,利用分摊法来解决晶体中所含的微粒数、晶体的化学式等问题．

1 晶胞中粒子数目的计算——均摊法

原则:晶胞任意位置上的1个原子如果是被n个晶胞所共有,那么每个晶胞对这个原子分得的份额就是1/n．

1) 平行六面体晶胞中不同位置的粒子数,根据均摊法情况如图1所示．

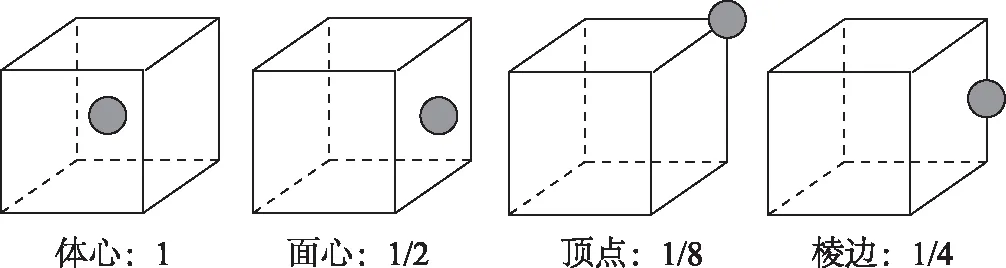
图1

2) 六棱柱、三棱柱、平面晶体结构单元中顶点、棱上的微粒的均摊情况见表1．

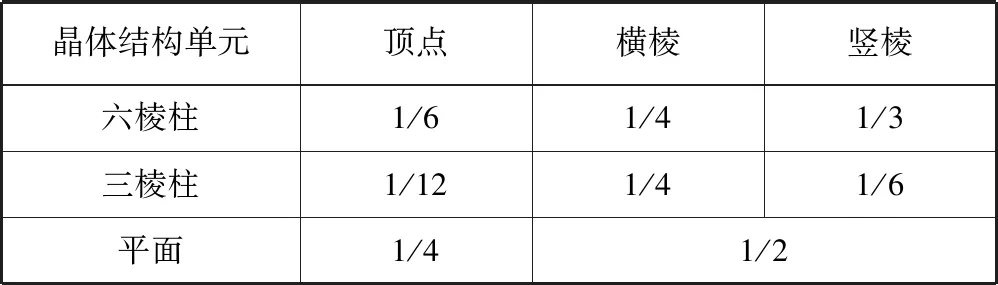
表1 各类晶体结构单元均摊情况

A. 8 B. 12 C. 24 D. 60

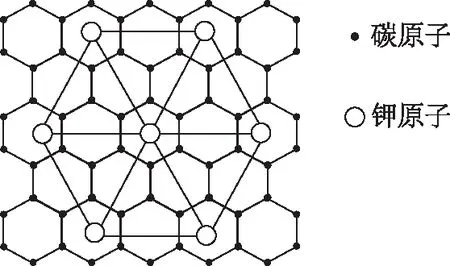
图2

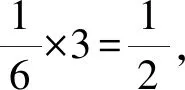
图3

A. 氮化碳属于原子晶体

B. 氮化碳中碳显-4价,氮显+3价

C. 氮化碳的化学式为C3N4

D. 每个碳原子与4个氮原子相连,每个氮原子与3个碳原子相连

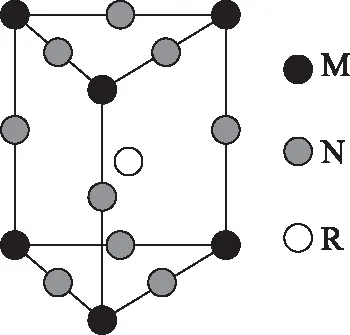
图4

A. 1∶4∶2

B. 2∶9∶4

C. 3∶8∶4

D. 3∶9∶4

2 晶胞密度的相关计算

对于立方晶胞,可建立如下求算途径:

1) 计算出1 个晶胞中粒子个数;

2) 推算出1 mol 晶胞中含粒子的物质的量;

表2 各类晶胞棱长与粒子半径的关系

4) 密度的单位常用g·cm-3, 晶胞参数的单位需要与密度单位统一,经常用到的换算关系有:1nm=10-7cm=10-9m,1pm=10-10cm=10-12m．

图5

图6

a3×9.00g·cm-3×NA=4×64g·cm-3,

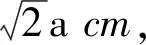
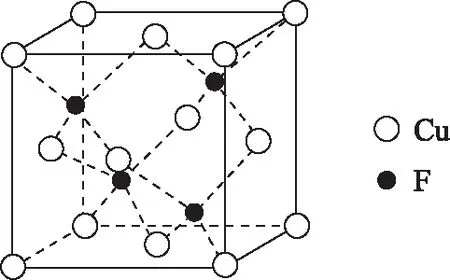
图7

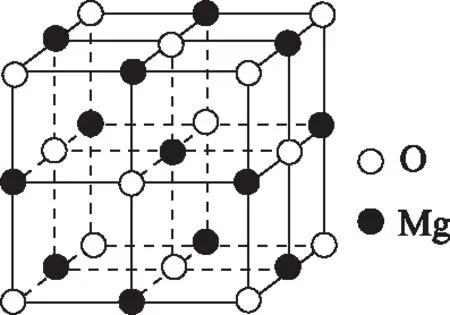
图8