基于随机抽样参数辨识的动力锂电池组仿真模型构建
2020-02-28钟志标彭育辉
钟志标, 彭育辉
(福州大学机械工程及自动化学院, 福建 福州 350108)
0 引言
建立精确的电池模型是评估和预测电池组剩余电量等问题的关键技术之一[1]. 若简单地将各单体电池的电阻、 电压等参数值进行叠加作为电池组的特征参数, 势必会忽略电池成组后的通风散热条件、 连接电阻、 绝缘条件等变化导致电阻的增大问题[2]. 另一方面, 电池经过多次充放电之后必然会出现电池组中各电芯性能参数的不一致问题, 而电池组的电量往往取决于电池组中的最低电动势的单体电池电量. 已有的电池组建模方法包括单体电池累积法、 最低电动势法和直接建模法. 单体电池累积法忽略了连接电阻导致实际电池端电压和实际得到的电压有较大偏差[3]; 最低电动势法需要花费大量的时间在建立电池模型和参数辨识上, 效率不高[4]; 直接建模法存在的不足在于没有考虑到电池组中各电芯参数的不一致性问题[5].
本研究以钴酸锂离子电池为研究对象, 基于单体电池模型的构建, 提出一种电池组等效模型建模方法. 通过抽样, 对样本单体电池进行参数辨识实验, 以样本电池的各性能参数的平均值和方差表征电池组各电芯的参数. 利用Matlab/Simulink仿真技术, 建立电池组的仿真模型, 以电动势最低的单体电池的电量表征电池组的剩余电量. 通过实际电池组的脉冲充放电实验得到电池电压的动静态特性, 与仿真结果进行对比, 验证本研究所提方法的有效性和准确性.
1 单体电池建模
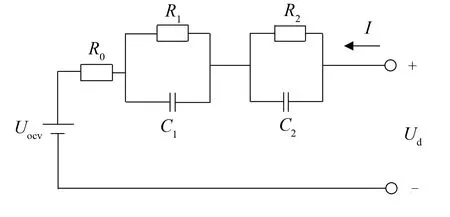
图1 二阶RC等效模型Feig.1 Second-order RC model
综合考虑电池管理系统芯片的计算速度和模型复杂度的问题, 采用二阶RC模型(图1)对单体电池进行建模. 图中Uocv为电池开路电压;Ud为端电压;R0为欧姆内阻;R1为浓差极化内阻;C1为浓差极化电容;R2为电化学极化内阻;C2为电化学极化电容.
根据基尔霍夫定律得到:
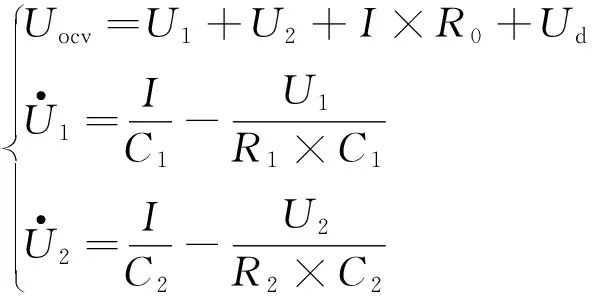
(1)
剩余电量百分比采用安时积分法计算:

(2)
式中: SOC初始为初始剩余电量;Q为电池容量.
将式(1)~(2)写成状态方程的形式, 即:

(3)
式中:UOCV(SOC)表示开路电压是SOC的函数;U1、U2为C1、C2两端电压;η为库伦效率;T为采样时间.
将方程(3)离散化, 得到方程的离散模型如下式所示:
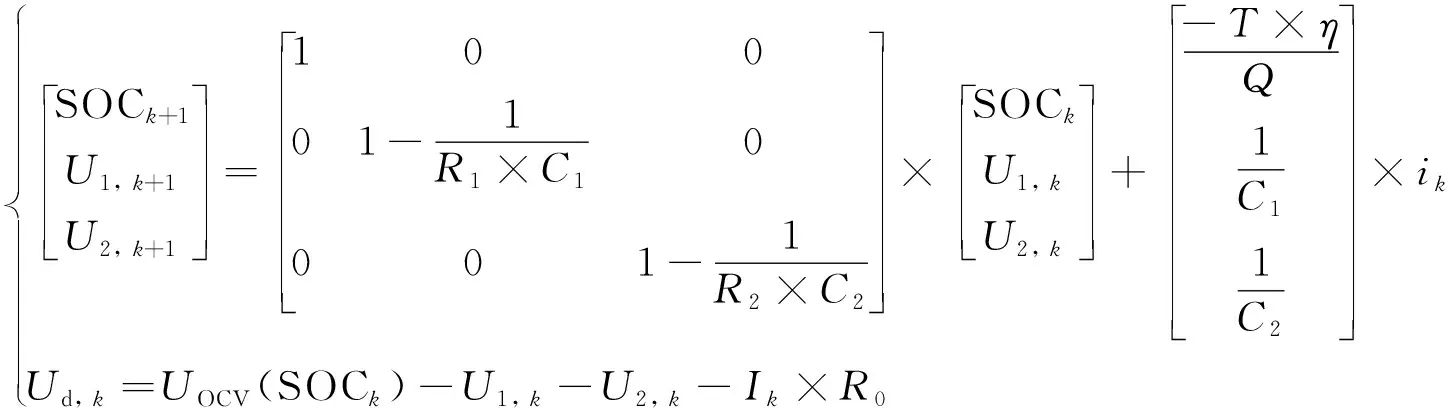
(4)
其中:k=1, 2, …,n(n为正整数). 为了准确揭示电池等效模型中电池特性参数之间的变化关系, 必须获取准确的容量、 充放电效率、 欧姆内阻、 极化阻容等参数值.
2 单体电池模型各参数的识别
2.1 电池的可用容量的确定
单体电池为格瑞普公司生产的软包钴酸锂离子电池(3.7 V, 23 A·h-1). 为了排除充放电倍率对电池容量的影响, 本研究采用厂家提供的标准充电电流(8 A)对电池进行容量辨识, 采用文献[6]中所述的实验方法对电池进行充放电实验, 环境温度为25 ℃, 充放电电流值为8 A. 实验结果如表1所示, 取电池可用容量为24.20 A·h-1.
2.2 电池的开路电压与剩余电量关系

表1 电池容量
为获取电池准确的开路电压 (open circuit voltage, OCV)和剩余电量 (state of charge, SOC)之间的关系, 对电池使用标准的充放电流进行实验. 通过该方法可有效避免因为充放电倍率选择不当而导致SOC-OCV曲线标定不准的问题. 充放电实验中保持环境温度(25 ℃), 电流0.2 C(8 A), 实验结果如图2所示. 图2是充电的SOC-OCV曲线和放电的SOC-OCV曲线, 可见充电和放电过程得到的曲线存在一定误差.
本研究对充电和放电过程求取平均值, 得到充放电平均值SOC-OCV曲线如图3所示, 对比了充电、 放电和充放电均值SOC-OCV曲线的模型精度后, 选取充放电均值SOC-OCV曲线作为电池模型关系曲线, 并对充放电均值SOC-OCV曲线进行7阶多项式拟合, 得到平均值SOC-OCV表达式, 如下式所示:
2.3 阻容的辨识
锂离子电池停止工作的瞬间, 电池的端电压会出现开始回弹的现象. 在充电状态下停止工作的瞬间出现电池端电压缓慢下降, 在放电状态下停止时端电压会缓慢上升. 针对以上电池状态出现的现象, 对电池组进行脉冲充放电实验, 以23 A(1 C)的放电倍率对电池放电3 min后静置5 min, 得到电流加载曲线和电压回弹曲线, 如图4~5所示. 因为在不同SOC下, 电阻的值会发生变化, 所以设计了SOC每隔5%进行放电并静置, 以获得在不同SOC下, 对应的不同的电池参数. 根据不同SOC下的端电压回弹曲线, 可以依次对回弹曲线进行处理得到不同SOC下的电池的阻容参数. 放电状态下SOC从100%放电到95%的端电压回弹曲线如图6所示.
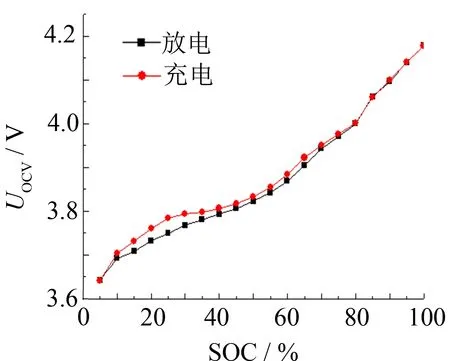
图2 充电和放电SOC-OCV曲线对比Fig.2 Comparison of charging and discharge SOC-OCV curves
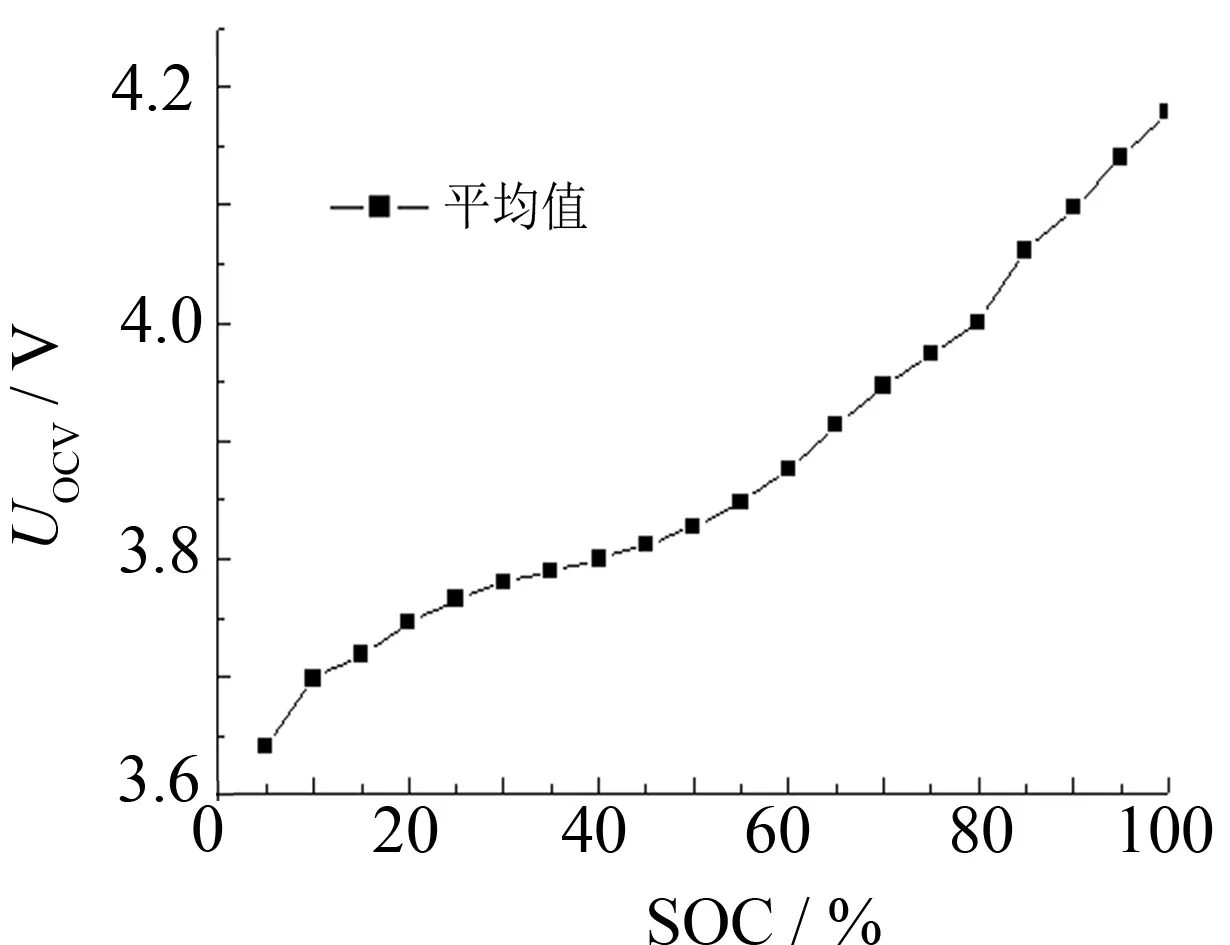
图3 充放电电压平均值拟合OCV-SOC曲线Fig.3 The average value of charge and discharge voltage fits OCV-SOC curve
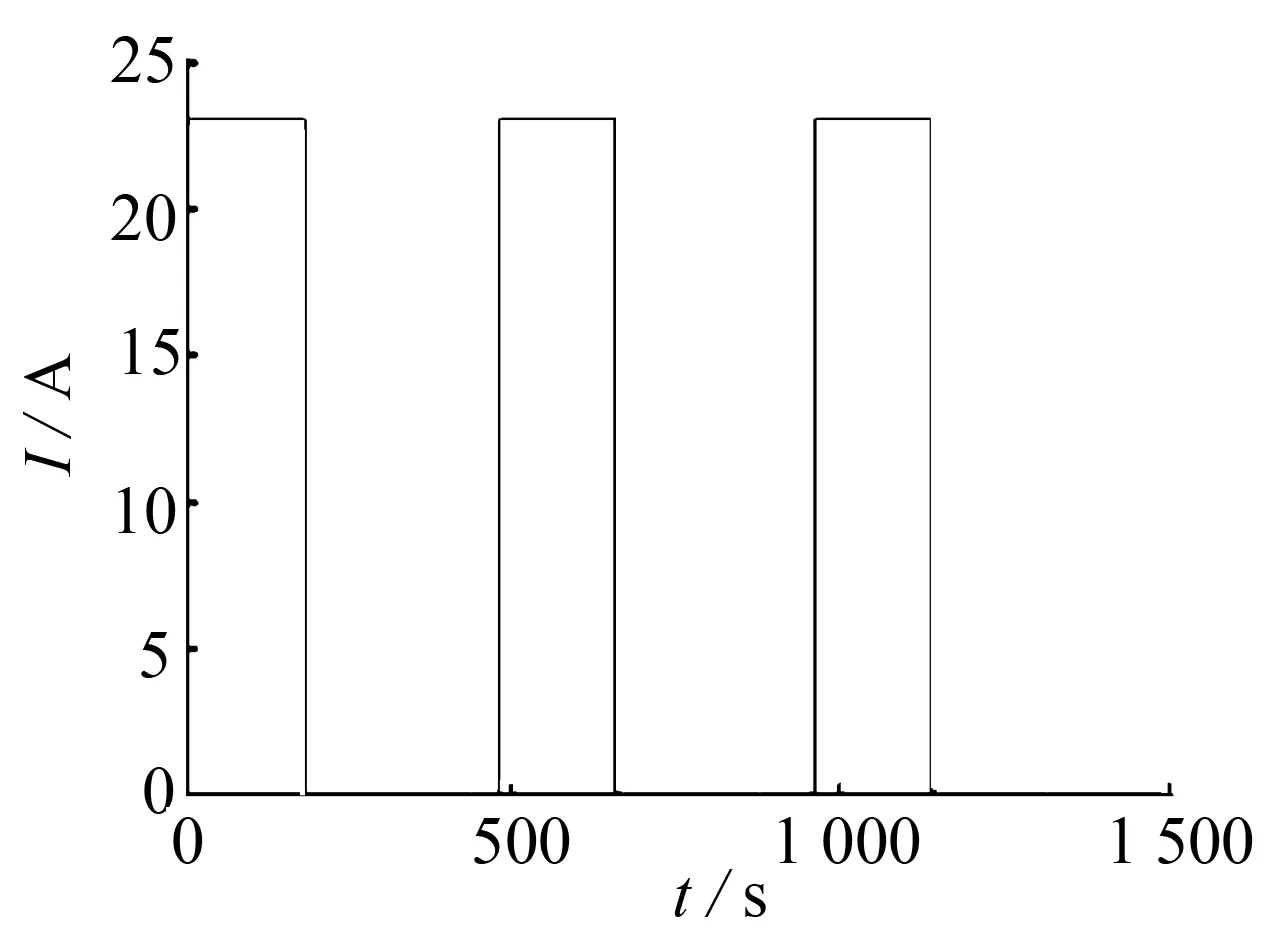
图4 脉冲电流加载曲线Fig.4 Pulse current loading curve
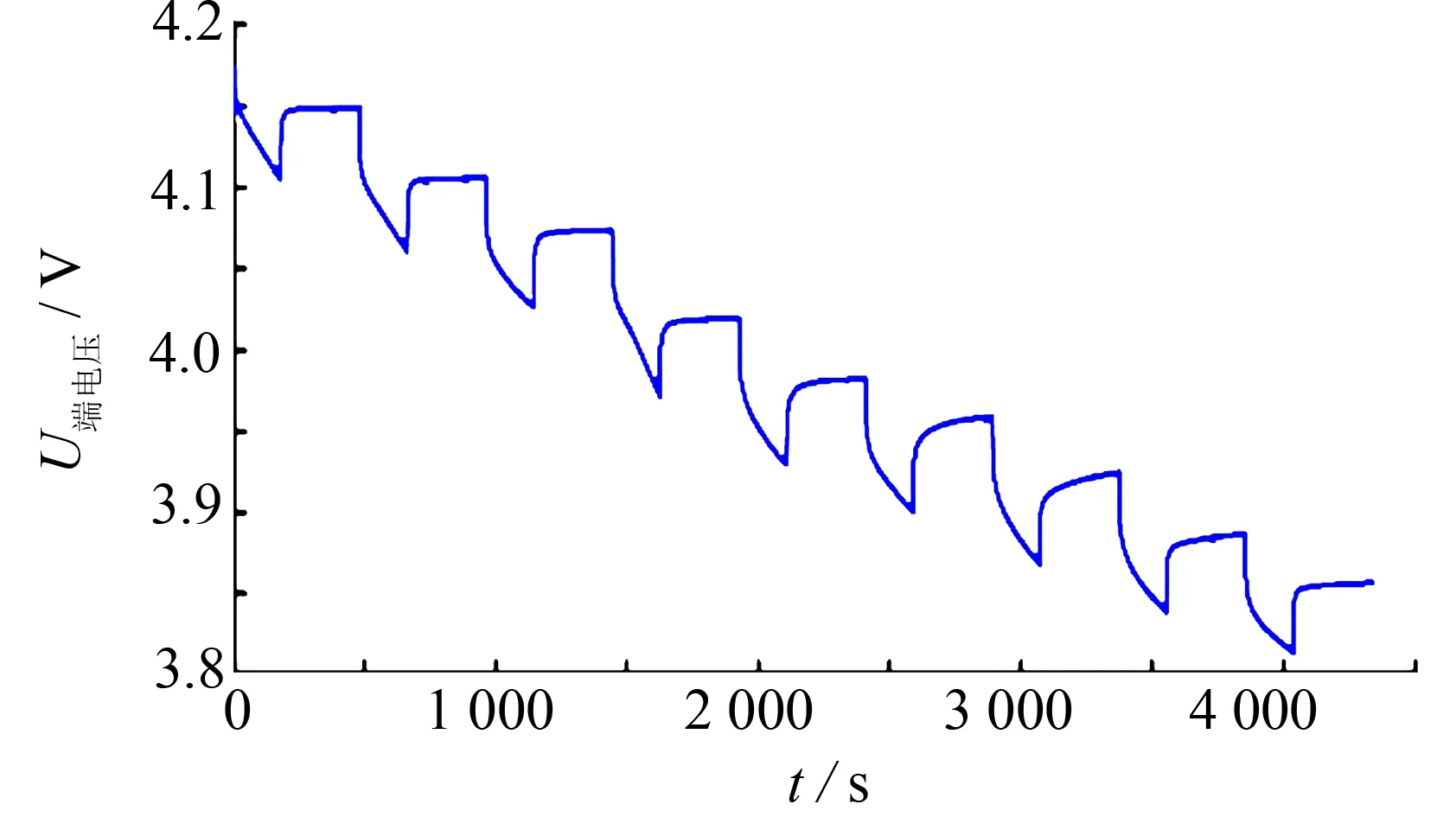
图5 电池的端电压回弹曲线Fig.5 Springback curve of terminal voltage of battery
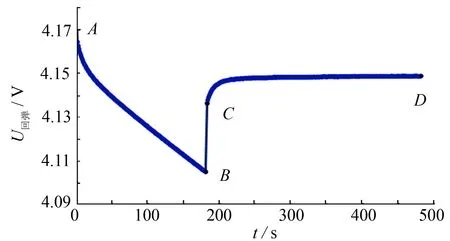
图6 100%放电到95%电压曲线Fig.6 100% rebound to 95% voltage curve
电池的欧姆内阻导致的电压回弹如图6中点B到点C所示, 所以欧姆电阻可以如下式计算得:
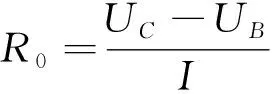
(6)
电池内部的极化电阻和极化电容导致的缓慢回弹电压如点C到点D所示, RC为零输入响应[7]. 端电压表达如下式所示:
(7)
令τ1=R1×C1,τ2=R2×C2, 则可得:
(8)
对点C到点D的端电压的数据按式子(8)进行拟合, 可求解a和c的值. 结合式子(7)~(8)可以求解单体电池模型的各参数值为:
(9)
3 电池组建模
对于单体电池数量较多的电池组, 在电池组建模过程中很难准确获得电池组中全部单体电池的性能参数值. 已有电池组建模方法中的最低电动势法存在建模繁琐的问题, 整体建模法未考虑单体不一致问题而导致电池模型误差较大. 本研究根据电池组中电池的容量、 内阻等参数符合正态分布的特点[8], 将最低电动势电池组建模法结合统计学方法, 抽取电池组中的部分电池作为样本电池进行参数辨识, 得到样本电池的性能参数. 然后对获得的参数进行统计学计算, 得到样本电池性能参数的平均值和方差, 来代表电池组性能特征参数. 基于二阶RC单体电池模型, 利用MATLAB输入样本电池参数的平均值、 方差和取值上下限生成符合正态分布的一组参数值, 将生成的一组参数输入到电池模型中, 结合最低电动势法来建立电池组模型.
3.1 电池组参数求解
根据文献[9]中对样本电池的选取方式, 对大学生方程式赛车动力电池系统的电池组(电池组中包含14个单体电池)取30%的样本, 即对5个样本单体电池进行电池参数辨识, 得到5个单体电池在不同SOC下的电池参数, 包括单体电池开路电压、 单体电池R0、 单体电池R1、 单体电池R2, 以及单体电池C2与SOC关系, 过程如第2节所述. 获取的单体电池开路电压、R1与SOC的关系如图7~8所示.
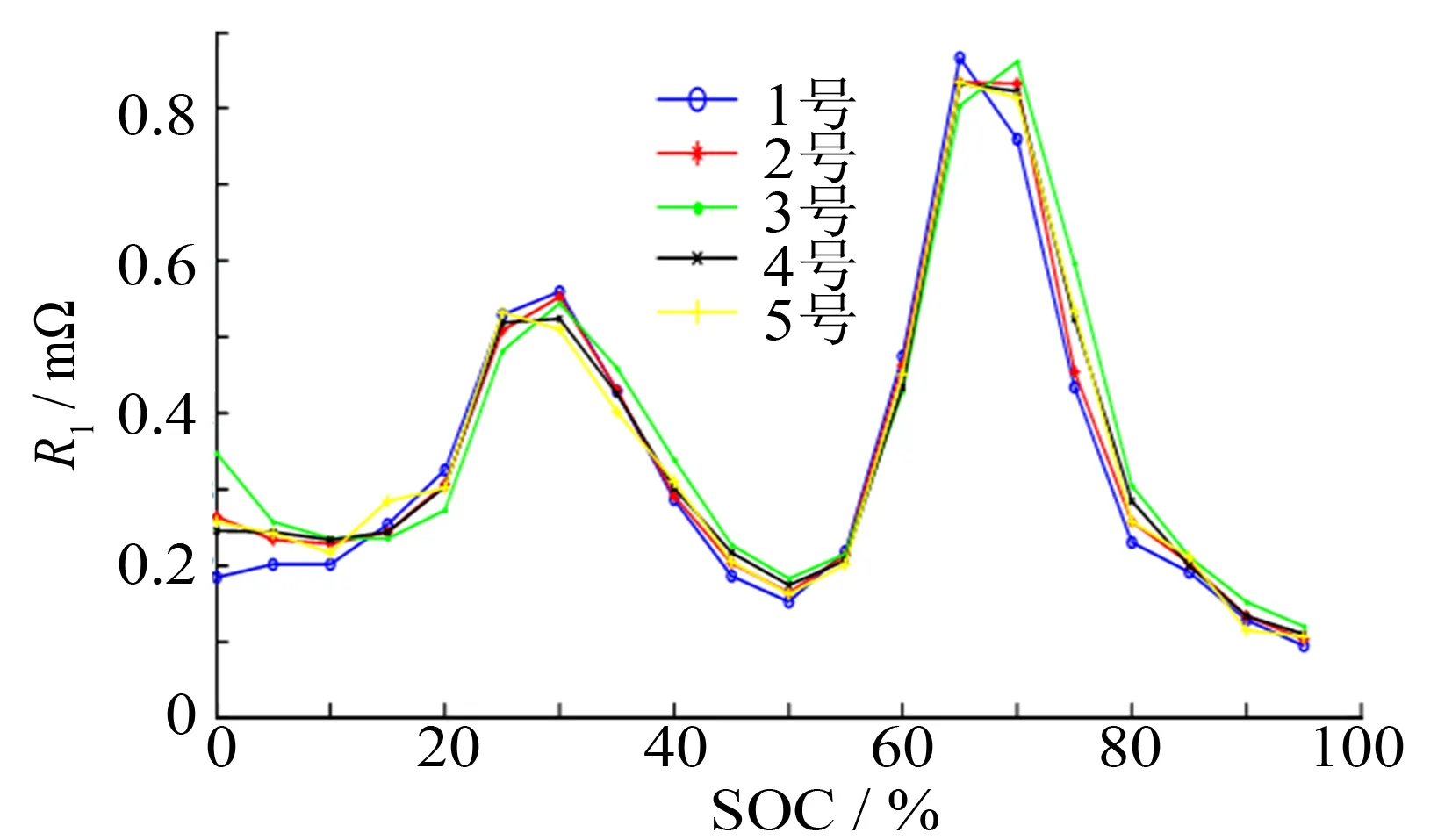
图8 单体电池R1与SOC关系Fig.8 Relationship between R1 and SOCof single cell
本研究以电池容量为例, 说明均值、 方差和分布区间的获取. 电池的容量只会受到温度和寿命的影响, 故对这5个电池容量进行平均, 获得容量平均值; 方差则是根据5个电池的容量数据求出; 取值的上下限是根据测试电池容量时所获得的5个电池中的最大容量值和最小容量值, 结果如下: 平均值为24.196 8,方差为7.795 86×10-5, 取值上限为24.21, 取值下限为24.18.
对上述数据进行统计分析获得样本的电芯在不同SOC下对应的各参数值. SOC=50%时的参数统计值如表2所示.
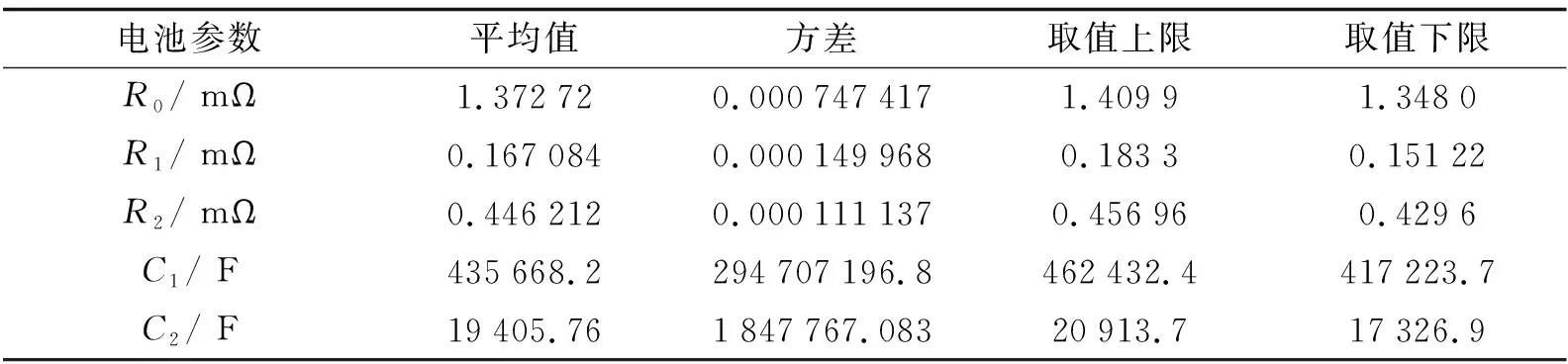
表2 SOC=50%时的电池特性参数数理统计值
3.2 电池组仿真模型构建
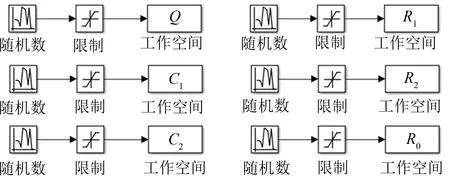
图9 生成电池组参数的模型 Fig.9 Generates the parameter model of the battery pack model
电池组的电量取决于电量最快达到极限值的电芯(充满或者放完), 电池的开路电压和SOC有着对应关系. 基于最小电动势法, 将单体二阶RC电池模型作为电池组模型. 电池组模型的参数来自于上述实验获得的样本参数的平均值和方差, 利用MATLAB/Simulink根据样本单体电池参数的平均值、 方差和取值上下限按正态分布生成电池组参数模型, 如图9所示, 运行该模块可以生成一组电池参数, 生成的电池参数(SOC=50%时)如表3所示. 在Simulink中建立电池组仿真模型, 如图10所示.

表3 SOC=50%时生成的参数

图10 电池组仿真模型Fig.10 Battery pack model
4 实验验证
在常温(25 ℃)下, 采用电池综合参数测试仪系统(江苏金帆电源科技有限公司μC-ZS08)对电池组(14串)进行电池脉冲充放电工况实验, 其记录的间隔为1 s, 电流工况数据如图11所示. 电池充放电设备可以采集电池组中所有单体电池的工作电压, 通过总线上传到上位机来存储每个单体电池在每个时刻的端电压. 将计算机仿真数据和设备实际采集到的数据进行对比, 为了更好地显示拟合的效果以及误差, 只截取了2 200 s的数据对其进行对比分析.
对比电池组实际放电实验和计算机仿真结果(图12), 从中可知电池组实际放电时最低电动势单体电池的电压曲线与仿真电压曲线拟合度较好. 仿真与实验的最大误差是出现在断开电池的瞬间, 详见图13, 误差为0.05 V, 出现此问题是由于放电过程中电池组突然由放电工况转为静置工况, 电流传感器无法及时反应而导致的. 其余工况下拟合的误差在0.01 V左右, 相对误差在0.2%左右. 对比文献[10-11]中的电池模型精度, 所提方法建立的电池组模型具有较高精度, 不仅能较好还原电池组的实际工作状态, 而且能为电池组建模节省大量电池参数辨识及建模的时间.
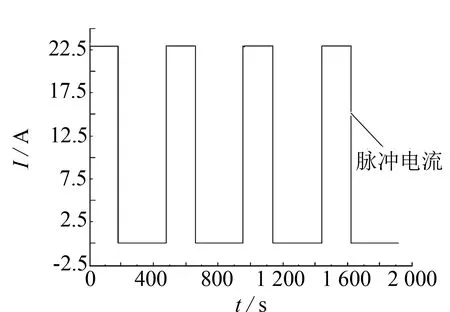
图11 脉冲放电工况实验Fig.11 Pulse discharge test

图12 电池组实验与仿真电压对比Fig.12 Batteries experiment and simulation voltage comparison
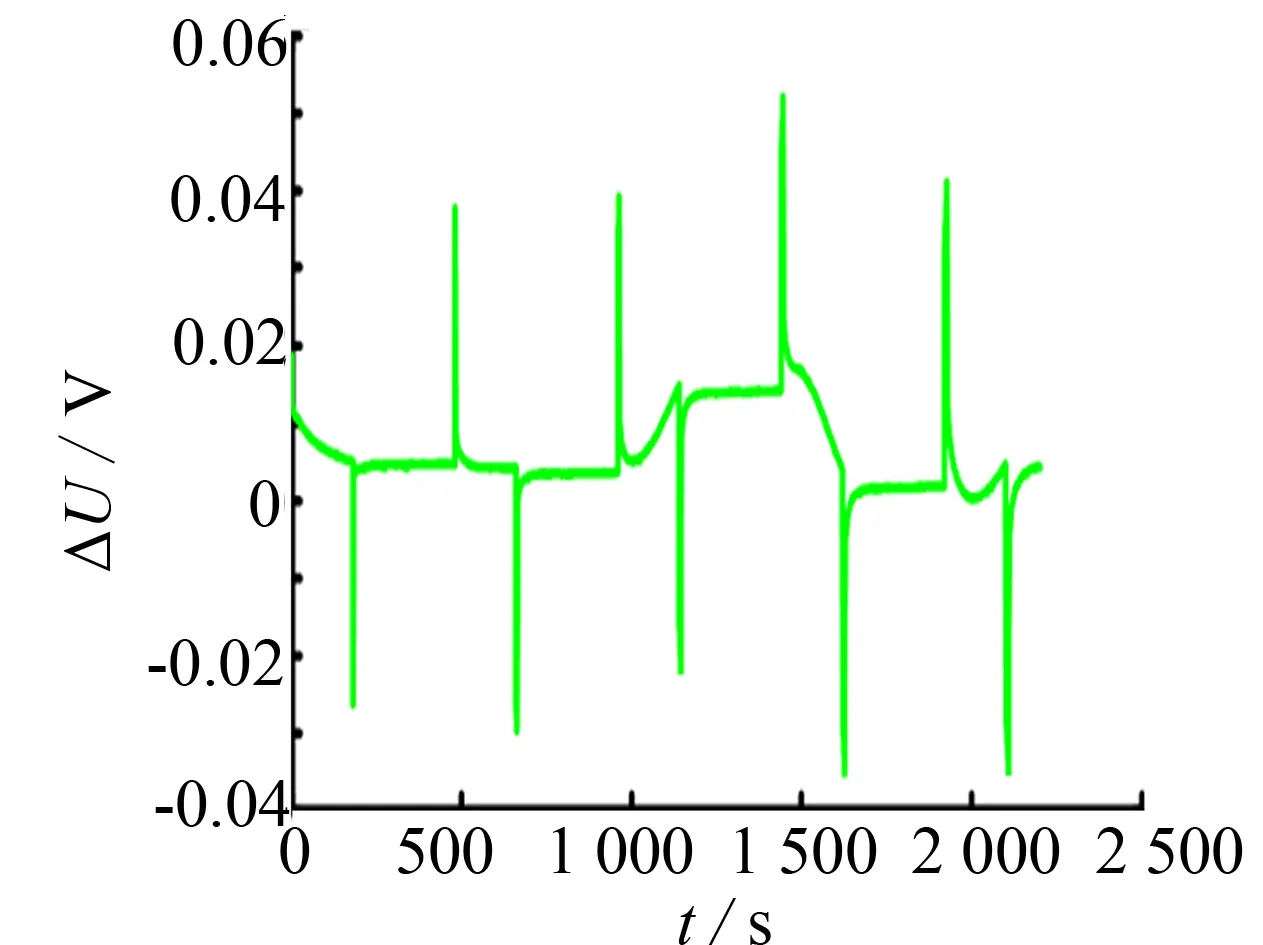
图13 仿真与实验误差电压值Fig.13 Simulated and experimental voltage error values
5 结语
本研究根据电池组中电池的参数(电阻、 容量等参数)呈现正态分布的特点, 提出了一种基于随机参数辩识方法, 建立动力锂电池组仿真模型. 通过对比仿真和实际充放电实验, 证明该方法能节省大量辩识电池参数和建立电池组模型时间, 且电池模型的精度也较为理想.
