基于学业质量标准的单个试题的命制与评价

【摘 要】学业质量标准反映了2017年版高中数学课程标准的最新成果，是学生学习数学课程后学业成就的表现。基于学业质量标准对单个试题的命制与评价进行探讨，从单个试题命制的背景与过程、单个试题评价以及数学关键能力赋分等角度展开，反思命题评价：命制试题离不开知识，忌空谈素养;评价要凸显过程性，遵循素养达成规律;评价要注重“双原则”，创新评价形式。

【关键词】学业质量;试题命制;数学核心素养

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2020）03-0019-04

【作者简介】孔德鹏，南京航空航天大学附属高级中学（南京，210007）教师，一级教师。

《普通高中数学课程标准（2017年版）》（以下简称“2017年版课标”）明确了学业质量标准，强调以数学核心素养及其表现为主要维度，对学生学业成就表现进行总体刻画。[1]另外，2017年版课标在“评价建议”中要求教师重视整体性评价和过程性评价，革新评价方式，注重评价的主体多元化、评价形式的多样化。数学核心素养的发展过程是循序渐进的，具有阶段性、连续性和整合性等特点，这就意味着命题评价要体现过程性和阶段性，不仅要关注素养水平实际情况，更要关注学生成长和发展的过程，关注学生在学习过程中的发展和变化。

单个试题命制是整张试卷命制的基础，值得关注与研究。笔者就如何进行素养导向的试题命制和如何注重发展学生数学素养的过程评价进行了积极探索。

一、单个试题命制的背景和过程

按照南京市课程教学计划，高一下学期的主题内容包括三角变换、解三角形、立体几何与解析几何初步。期中考试的基本定位为阶段性学业质量检测，涉及内容为三角变换、解三角形、立体几何等有关知识。就数学学科核心素养评价而言，笔者认为应用题可以重点评价考生的数学抽象、数学建模、直观想象、数学运算等核心素养水平。笔者尝试从教材中寻找命题素材，又从2017年版课标中搜索题源，试图命制一道较好的试题。

1.教材例题。

“解三角形”是苏教版高中数学必修5的第一章内容，在教材中有这样一道例题，呈现如下：

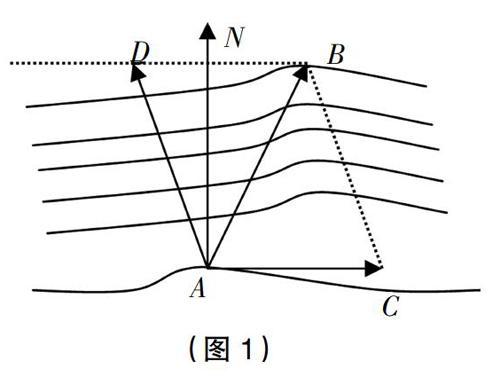
在长江某渡口处，江水以5km/h的速度向东流。一渡船在江南岸的A码头出发，预定要在0.1h后到达江北岸B码头。设■为正北方向，已知B码头在A码头的北偏东15°，并与A码头相距1.2km。该渡船应按什么方向航行？速度是多少（角度精确到0.1°，速度精确到0.1km/h）？

这道题是“余弦定理”一课的例题，是以学生熟悉的过河问题为背景，题目表述中涉及向量（位移）等知识，其作用是提升学生的数学建模素养（抽象出三角形模型）和数学运算素养（有序利用余弦定理和正弦定理解决问题），兼有直观想象和数学抽象素养。例题教学要突出发现和提出问题的过程，引导学生用数学语言表达问题，建立解三角形模型;注重分析和解决问题，理解三角形的运算对象，利用运算法则，探究运算思路，获得结果。这是一道经典的数学建模题，具有很好的育人价值。

2.课标例题。

无独有偶，笔者发现2017年版课标中的案例32也是一个过河问题，题目呈现如下：

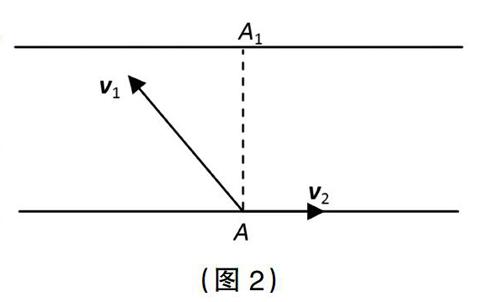
长江某地南北两岸平行。如图2所示，江面宽度d=1km，一艘游船从南岸码头A出发航行到北岸。假设游船在静水中的航行速度v1的大小为10km/h，水流的速度v2的大小为4km/h。设v1和v2的夹角为θ（0°<θ<180°），北岸的点A1在A的正北方向。

（1）当θ=120°时，判断游船航行到达北岸的位置在A1的左侧还是右侧，并说明理由。

（2）当cosθ多大时，游船能到达A1处？需要航行多长时间？

2017年版课标说明，这道题目是以平面向量知识为载体，以确定游船的航行、航程为任务，借助理解运算对象、运算法则，探寻運算思路，设计运算程序，实施运算过程等数学思维活动，考查学生数学运算素养水平一、水平二、和水平三的实际表现。[1]

综上分析，笔者觉得这个案例立意非常好，适合改编为一道阶段性检测题。本着体现教学评价的过程性和发展性原则，再结合本区学情实际，题目分数设置满分15分，题目改编如下：

长江某地南北两岸平行，如图2所示，江面宽度d=1km，一艘游船从南岸码头A出发航行到北岸。假设游船在静水中的航行速度v1的大小为10km/h，水流的速度v2的大小为4km/h。设v1和v2的夹角为θ（0°<θ<180°），北岸的点A1在A的正北方向。

（1）当cosθ多大时，游船能到达A1处？需要航行多长时间？

（2）当θ=120°时，判断游船航行到达北岸的位置在A1的左侧还是右侧，并说明理由。

二、单个试题的评价

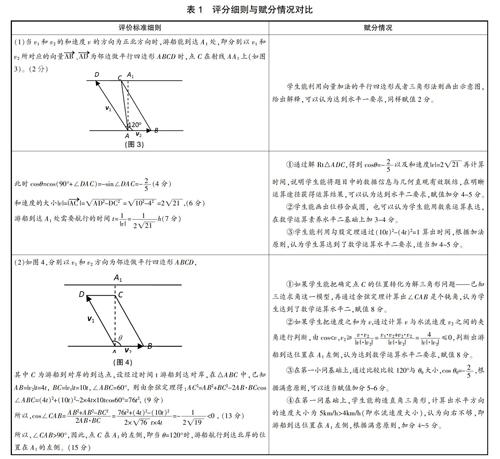
在实际的阅卷工作中，发现学生的答题情况并不符合评分标准的逻辑顺序，所以我们在体现“满意原则”和“加分原则”的基础上，基于素养导向，在考查学生直观想象、数学抽象、数学建模、数学运算等素养的立意上适当赋分，两小题分别给7分、8分，具体见下页表1（评分细则是评分标准，赋值加分不能超过每小题满分）。

需要强调的是，第二小题赋分栏③④两种情况不能给满分。这两种思路都是基于几何直观的分析，缺乏“以形助数”的过程。学生紧紧抓住“向量”这一工具，只想在向量的情境里解决问题，这暴露了思维的单一性。这两种解法里面有逻辑推理（将位置关系用数学语言表达），也有数学运算（用计算说理），在满意原则和加分原则基础上可以给予4 ～ 6分，表达较好的给6分。这两种解法的弊端是最后还是回到图形上，过于依赖直观，不如标准和①②情况，缺少严谨的代数推理。

参照参考文献[2][3]赋分方案[2]：由各项分值确定题目的分值，一级、二级、三级水平分别计x分、x+1分、x+2分。若照此方案赋分，针对本题的两小问，我们取x=1，则本题目的赋分如下页表2。

数学关键能力的考查要立足数学核心素养水平，水平越高，赋分越高，认为能力越强，对于同一道题目，学生表现出的素养可能是单一的，也可能是多项的，评价时需要有侧重点，依据满意和加法原则做灵活处理。

三、命题与评价反思

通过参与本次期中考试题目的命制与改卷工作，反思当前新课程标准落实情况，还有很多事情要抓落实。从本例单个试题的命制与评价过程来看，有三个方面的思考。

1.命制题目离不开知识，忌空谈素养。

基于数学核心素养的课程目标制订是以知识作为核心素养的生成本源为逻辑线索。[2]可见，知识是数学核心素养的具体载体，题目的命制离不开知识点铺设。在命制此题的过程中反复思量琢磨，立足教材例题育人价值的挖掘，再结合新课程标准案例，试图创造一种“结构不明”的问题情境，以课本为基础，又适当高于课本，引导学生展开问题探究。在平时教学中要注重对解题思路的挖掘，注重教“怎么想”——培养学生提出问题与分析问题能力。就本题而言，还可以从向量运算、数量积、勾股定理、解斜三角形等角度解决问题，启示我们要注重对问题本质的剖析、多角度审视问题、多元表征问题，培养学生广阔的发散思维能力，提升学生数学抽象、逻辑推理、直观想象、数学运算、数学建模等素养。

2.评价要凸显过程性，遵循素养达成规律。

学业质量的评价服务于学生数学核心素养的达成，素养达成是循序渐进的，必然要求教師注重评价的过程性，不宜采用“一刀切”“贴标签”等极端方式，重视评价的整体性和阶段性，重视过程性评价。学生的思路、推理不可能完全按照评分标准，教师要研究学生答题的亮点、素养点生成得分点。允许和标准答案不同，鼓励学生发散思维和创新精神。仔细研究学业质量水平一和水平二（兼顾水平三），通过将知识迁移到熟悉或关联的情境中，循序渐进、螺旋上升地发展学生素养。

3.评价要注重“双原则”，创新评价形式。

评价结果指向学生数学学习的信心、兴趣、习惯的培养，促进学生全面发展。注重“满意原则”“加分原则”的使用，挖掘学生答题中的思维点，判断学生“三会”情况，鼓励学生思考，关注学生思考内容和思维质量，进而优化思维过程。通过赋分进行评价时，不仅要以命题立意倾向设置得分点，也要灵活处理解题过程中素养水平的落实点。既要注重素养立意，也要注意解答的通法、优解等多种解法的交融。总之，学生实际答题的复杂性要求教师创新评价方式，不能唯“标准”论。

【参考文献】

[1]教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018：74-79.

[2]喻平.基于核心素养的高中数学课程目标与学业评价[J].课程·教材·教法，2018（01）：80-85.

[3]渠东剑.素养导向下的学业质量评价探讨[J].数学教育学报，2019（10）：59-64.