基于BP神经网络的时栅时序预测测量研究

郑方燕陈鹏霖石海峰颜 路

(重庆理工大学，机械检测技术与装备教育部工程研究中心，重庆 400054)

0 引言

数控系统是数控机床的关键功能部件，是保证机床加工精度的重要组成部分，由于增量式光栅及其配套的数控系统研制较早，现在已经在工业生产中大量使用[1]。时栅位移传感器为课题组研制的一种新型传感器，以时空转换思想为理论基础，通过对时间的精准划分实现对空间的精确测量，具有抗干扰能力强、测量精度高等特点，在可靠性以及成本上都有较为明显的优势[2]。但时栅由于是等时采样，而光栅是利用莫尔条纹进行空间位置测量，二者因工作原理不同，如将时栅直接应用于数控系统会出现采样周期不同步和采样空间不同步的问题,无法直接与增量式数控系统相匹配，导致无法直接应用于数控系统[3]。本文针对上述情况，以不改变数控系统的运行原理为基础，提出一种把时栅应用到增量式数控系统的新方法。此方法将时栅按等时采样得到的时域信号视为一个时间序列，利用神经网络对时间序列进行分析、预测，并将其转换成空域信号，使之与增量式数控系统相匹配以实现增量式测量，同时将预测理论应用到本方法，以解决时栅传感器应用到增量式数控系统时的动态位置反馈误差问题，以实现高精度位置测量。

1 信号转换原理

时栅根据时空坐标转换原理研制而成，其基本原理如图1所示，在空间内构建一个匀速运动的坐标系v，让运动坐标系分别掠过定测头Pb和动测头Pa，记掠过Pb的时刻为T1，掠过Pa时刻为T2，求出坐标系掠过动、定测头的时间差(T2-T1)，就可以得出动测头相对定测头移动的角度值[4]。

θ=v(T2-T1)=vΔT

(1)

式中：v为匀速坐标系的运动速度；ΔT为坐标系相继掠过动、定测头的时间差。

图1 时栅测量原理

时栅为等时采样传感器，每隔一定时间间隔采集一次数据，设前N个时刻Ti-n，Ti-n+1，…，Ti-1采集到的角度值分别为θi-n，θi-n+1，…，θi-1，以此实测的N个值为样本，采用MATLAB神经网络对其进行分析，在Ti-1时刻通过BP神经网络模型预测出下一个采样时刻时栅数控转台的角度值，在下一个周期内把角位移增量Δθ(Δθ=θi-θi-1)以增量式脉冲信号发送给数控转台控制系统，控制系统发送脉冲驱动转台转过相应的角度值，采用此方法就可以把绝对式时栅位移值转换为增量式连续脉冲信号。具体实现方法如下：

Ti-1到Ti的位移增量Δθ采用脉宽调制PWM(pulse-width modulation)的方式发送至数控系统，其脉冲个数为

(2)

式中：Q为脉冲当量；ei-1为上个周期的误差值，即Ti-1与Ti的预测误差。

Ti+1时刻，通过式(2)利用时栅实测值与上一个预测值进行比对，对误差进行修正，提高系统输出精度。Ti时刻至Ti+1时刻的预测误差ei+1可以由式(3)得到：

ei+1=Δθi+1-ei-(θi+1-θi)

(3)

相应地，从Ti-1时刻至Ti预测误差ei可由式(4)得到：

ei=Δθi-ei-1-(θi-θi-1)

(4)

结合式(1)和式(3)，得到实际发出脉冲个数为

(5)

如式(5)中表达，此方法不仅可以实现时域信号到空域信号的转换，而且可以进行实测值与预测值的比对，从而用实测值对预测值进行修正，消除时栅传感器在预测测量中的累积误差。

2 位置预测方法

BP神经网络已被广泛应用于预测测量领域，它具有强大的泛化能力，可以将输入集中样本点的给定邻域映射到输出集中点的某一邻域，再经过训练后，可以使网络的输出值在指定范围内达到预期的精度[5]。本项研究中，将时栅的绝对式实测角度值发送至输入层后，由输入层的神经元再将其传递给中间层(隐层)，时栅信号在中间层神经元激活函数的作用下进行变换处理后被传输至输出层，输出层将下一个周期预测角度值的结果输出至数控系统，由此就实现了时栅信号在BP神经网络中的一次完整的正向传播。基于BP神经网络的时栅时序预测测量过程如下所述：

(1)信号正向传播过程。以一组时栅实测角度值θi-n，θi-n+1，…，θi-1共N个作为输入信号，任意一个角度值用i表示，中间层神经元的个数为P+1个，用j表示，输出层的神经元个数为o，用k表示。训练样本集为任意一组时栅数控系统采集信号θ=(θ1,θ2,…,θr,…,θn)，在神经网络中与之对应的训练样本为Xr=(xr0，xr1，xr2,…,xrq),r=1,2,…,n，其中xr0=-1；神经网络的实际输出为经过BP神经网络预测后的时栅预测角度值zr=(zr1,zr2,…,zro)；时栅在下一周期的实测角度值d作为BP神经网络的期望输出值，dr=(dr1,dr2,…,dm),r=1,2,…,n，网络通过学习期望值之间的内在联系以提高预测的准确度。设m为迭代次数，作为训练样本的实测角度值通过输入层传递给网络，信号正向传播过程如式(6)～式(9)所示：

(6)

(7)

(8)

(9)

式中：vij、ujk分别为输入层与中间层，中间层与输出层的权值。

时栅测量角度值Xr由式(6)经过处理，得到中间层的输入Ij，Ij被传递至中间层后由式(7)计算得到输出yj，yj与中间层神经元权值ujk乘积的和为Ik，Ik经过输出层神经元运算处理后的输出的信号由zk表示，若输出层的任一神经元误差信号为

erk(m)=drk(m)-zrk(m)

(10)

则输出所有神经元的误差总和为

(11)

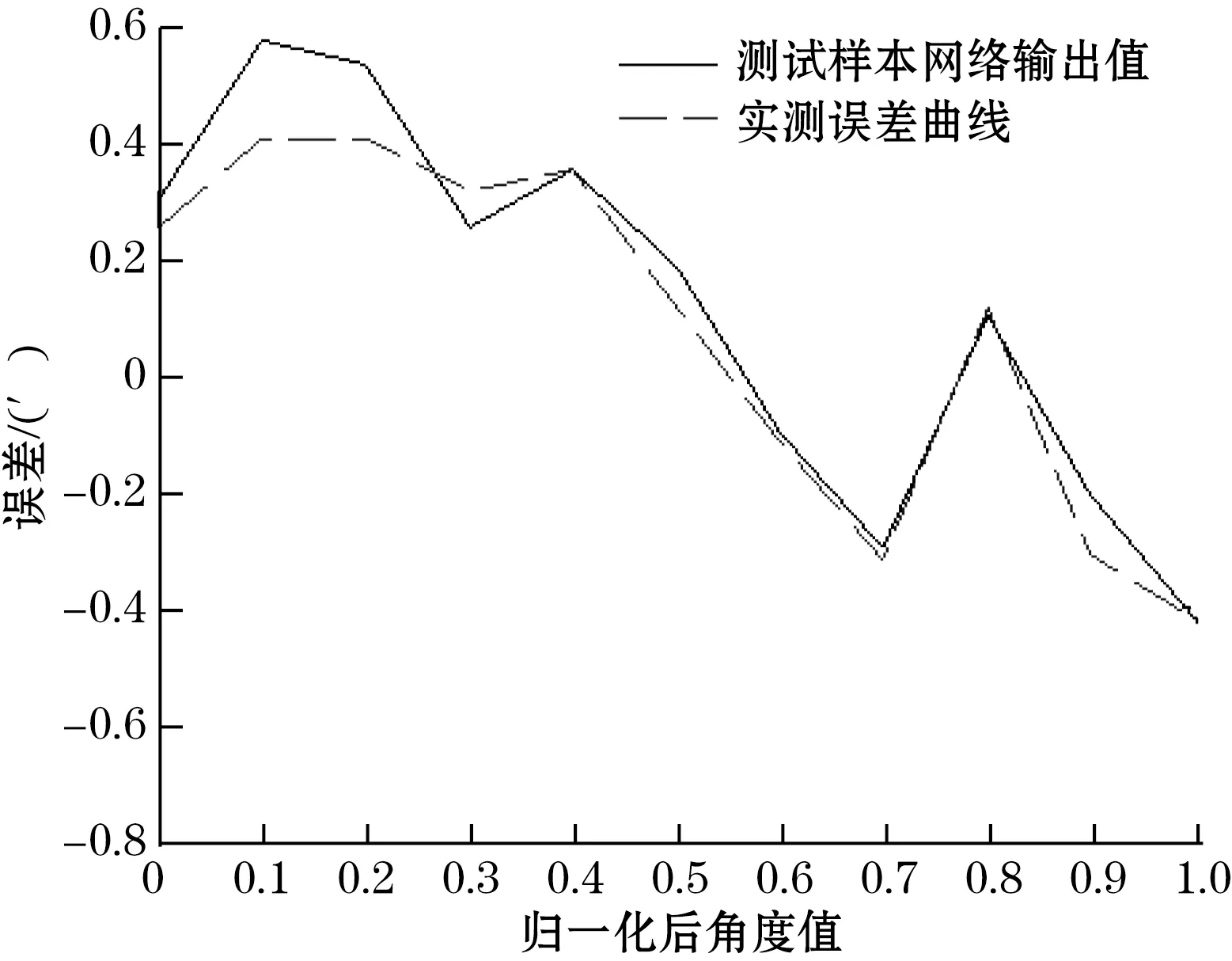
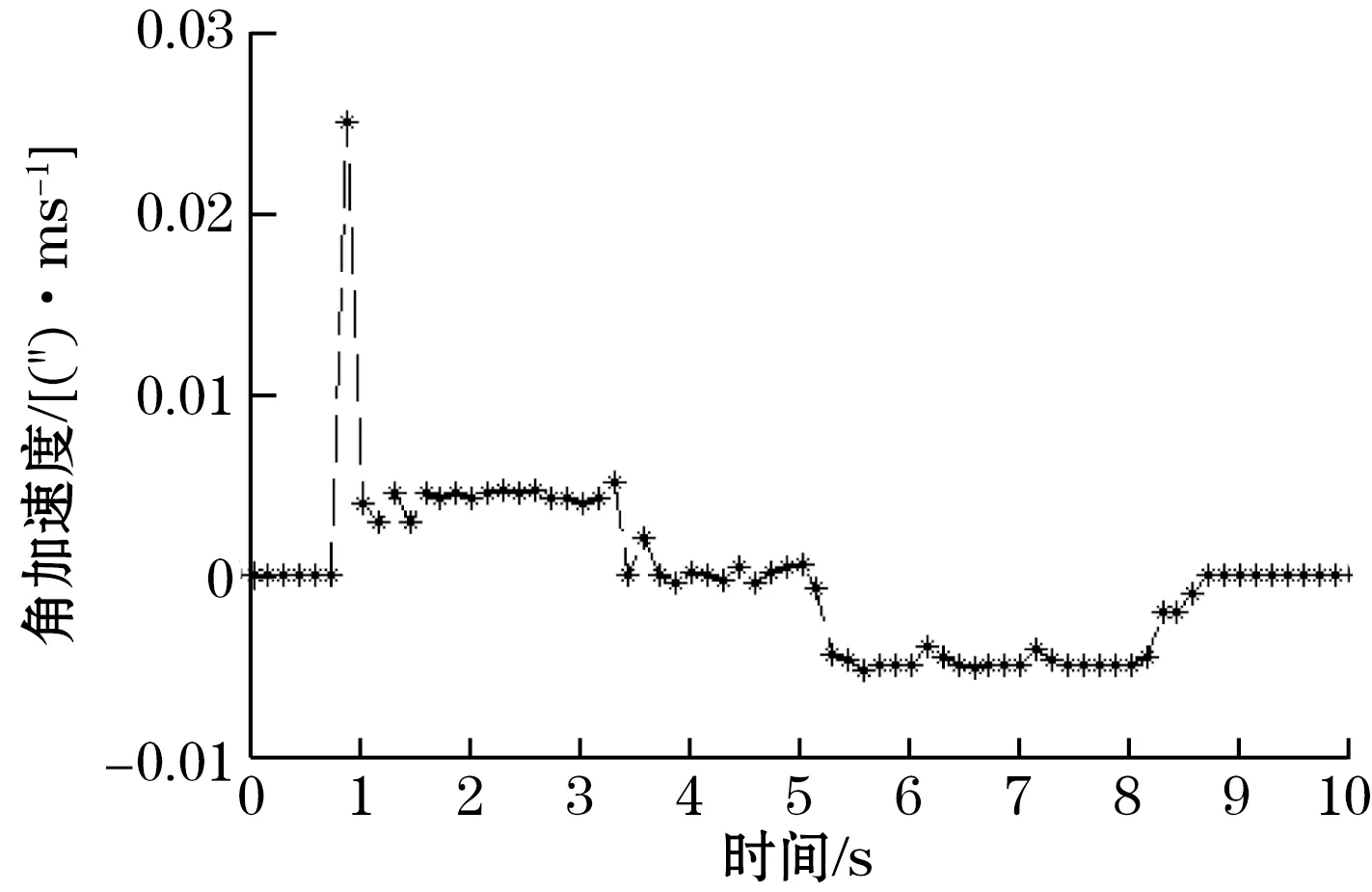
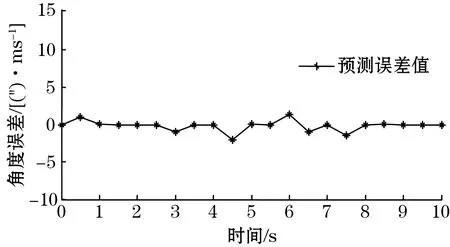
当E(m)

(2)反向传播过程：输出层输出的角度值与时栅下一个周期的测量值之间的差值即为误差，本次研究的误差范围为±2″，若误差不在此范围内，则使用神经网络的反馈调整来连续校正网络的权重，使得实际输出接近预期值。反馈调节的具体计算如下：

(12)

ujk(m+1)=ujk(m)+Δujk(m)

(13)

(14)

vij(m+1)=vij(m)+Δvij(m)

(15)

式中η为学习速率，是给定的常数。

通过式(12)～式(15)求得权值后进而可以调节输出值与期望之间的误差，最终得到最优解后继续转向式(6)，开始正向传播过程。

3 实验研究

3.1 仿真实验

为了验证前述理论，使用MATLAB做了仿真实验，将时栅采样值作为BP神经网络的输入，设置网络结构为单输入-单输出；由于实测角度值在0°～360°之间，为了减轻网络的计算负担，对数据进行归一化处理，使其长度为1，输入输出范围在(0～1)之间。为了使神经网络输出曲线与实测曲线的拟合效果达到最好，可以根据Kolmogorve定理[6]来确定隐层神经元和输出层神经元的个数，此次实验中分别设置为6和9。转移函数为purline(线性函数)。训练周期epoch=2 000，目标goal=0.02，学习速率lr=0.01，显示间隔show=50。时栅实测角度值作为输入数据经网络处理后的输出值与实测结果对比曲线如图2所示。

图2 实测曲线与输出曲线

由图2可知网络的逼近误差在±2″的范围内波动，符合实验的要求。

网络的学习能力不仅包括记忆已输入的数据，还包括学习样本的内在规律，即网络对陌生样本的适应能力，它的训练也是检验网络学习能力的一部分，经训练测试样本后得到的网络输出值的泛化能力曲线如图3所示，在经过泛化能力的训练后，网络的输出值与实测误差值的范围为±0.6″。由此可见经过泛化处理后的网络对测试样本数据处理能力得到进一步的提高，从算法的角度减小了网络预测误差，这为后续的实验验证提供了良好的基础。

图3 泛化能力曲线与实测误差曲线

3.2 转台实验

搭建了如图4所示的实验平台。平台由森创57BYG3步进电机、时栅、海德汉RON886圆光栅、RT275立卧数控转台和西门子数控系统等几部分组成。西门子数控系统控制电机驱动转台运动，光栅和时栅为了保证测量精度采用弹性联轴节同轴安装，在转台的带动下做同速运动。圆光栅测量值作为转台转过角度值的真值，时栅测量值作为转台角度实测值，二者测量值的差值即为BP神经网络应用于时栅数控系统后的测量误差。转台由任一位置开始转动，计算机每隔100 ms采集1次当前角度值。图5、图6分别为时栅数控转台的角速度变化曲线和角加速度变化曲线。由图5、图6可知，转台角速度和角加速度曲线在刚开始的1 s内变化范围较大，其余的时间变化都较平稳，可以舍去0～1 s内数控系统采集得到的数据，剩余时间内采集得到的数据符合按时间序列采样的角度值对平稳度的要求。

图4 实验平台

图5 数控转台角速度曲线

图6 数控转台角加速度曲线

数控系统测得的角度为时栅实测值，根据时栅测量值与光栅测量值之间的误差来调节网络的权值进而使网络可以拟合出误差曲线。图7为选取上述实测数据，利用实验对其验证后的实际效果图，图8为时栅预测数据与光栅实测数据的误差曲线。由结果可知，BP神经网络模型对时栅数控转台预测出的角度值与光栅实测角度值之间的误差在±2″内，说明模型可以对时栅角度值可以进行很好的预测，从而说明将时栅代替光栅应用到增量式数控转台系统中是完全可行的。

图7 实测值与预测值

图8 误差曲线

4 结论

针对时栅应用于全闭环增量数控系统中所遇到的由于时空不同步，时时不同步引起的动态误差问题，本研究提出一种利用BP神经网络对角度值进行预测的方法，对按等时采样得到的角度值进行预测得到下一时刻的角度位移值，并在下一个扫描周期内以脉冲信号的方式将角位移信号发送至数控系统，以实现绝对式时栅信号由时域向空域的转变。采用此方法，可以使绝对式时栅应用于增量式光栅数控系统中出现的采样周期不同步和采样空间不同步的问题得以解决。实验表明，采用此方法后，实现了时域信号向空域信号的转换，经实测，预测测量误差的波动范围为±2″，满足时栅数控转台对精度的要求。