Optimal index shooting policy for layered missile defense system

LI Longyue,FAN Chengli,XING Qinghua,XU Hailong,and ZHAO Huizhen

Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China

Abstract:In order to cope with the increasing threat of the ballistic missile (BM) in a shorter reaction time, the shooting policy of the layered defense system needs to be optimized.The main decisionmaking problem of shooting optimization is how to choose the next BM which needs to be shot according to the previous engagements and results, thus maximizing the expected return of BMs killed or minimizing the cost of BMs penetration. Motivated by this, this study aims to determine an optimal shooting policy for a two-layer missile defense (TLMD) system. This paper considers a scenario in which the TLMD system wishes to shoot at a collection of BMs one at a time,and to maximize the return obtained from BMs killed before the system demise. To provide a policy analysis tool, this paper develops a general model for shooting decision-making,the shooting engagements can be described as a discounted reward Markov decision process. The index shooting policy is a strategy that can effectively balance the shooting returns and the risk that the defense mission fails, and the goal is to maximize the return obtained from BMs killed before the system demise.The numerical results show that the index policy is better than a range of competitors,especially the mean returns and the mean killing BM number.

Keywords:Gittins index,shooting policy,layered missile defense,multi-armed bandits problem,Markov decision process.

1.Introduction

These years,ballistic missile(BM)technology has spread to more and more countries.Nations all over the world are developing missiles capable of reaching enemies.One important mission of the strategic defense is to develop an integrated, layered ballistic missile defense (BMD) system to defend the homeland, deployed forces, allies, and friends from ballistic missiles attack [1]. The BMD system is based on a multilayer defense concept and therefore contains more than one defense weapon; it will include different types of defense weapons located on land or ships used to destroy BM [2]. A two-layer missile defense(TLMD)system includes exoatmospheric high-layer interceptors(EXOHI) and endoatmospheric low-layer interceptors (ENOLI), such as THAAD mid-range EXOHI and PAC-3 short-range ENOLI[3].By now,the most difficult problem of terminal missile defense is that the time that can be used to intercept the target is very short.Short timelines not only stress the detection,tracking,and command and control of a defensive system, but also require a very efficient interceptor shooting policy[4].In order to cope with the increasing threat of BMs in a shorter reaction time,we must optimize the shooting policy of the TLMD system, a well-designed shooting policy should be done.The aim of this study is to determine an optimal shooting policy for the TLMD system.

Research has been performed on system effectiveness,attack-defense game, framing analysis, decision analysis,reaction-diffusion differential system and interceptor’s allocation against incoming BMs,but very little research has been conducted on the interceptor’s shooting policy with complex multi-wave attack of BMs [5–16]. Gittins first proposed the Gittins index to calculate the optimal allocation over time of a single resource among a collection of bandits which are in competition for it.We call such problems multi-armed bandit (MAB) problems [17,18]. Gittins has proposed a series of calibration indices,which are now commonly referred to as Gittins indices; he showed that the index policy which always directs the key resource to the projects with the highest current index is optimal[19].Agrawal considered MAB problems with switching cost, defined uniformly good allocation rules, and restricted attention to such rules [20].The Gittins index require that passive projects should remain frozen inhibits applicability.Thus,Whittle introduced an important but intractable class of restless bandit problems which generalize the multi-armed bandit problems of Gittins by allowing state evolution for passive projects[21–23].In recent years,many researchers have made innovative research on the theory of Gittins index and its application in the fields of resource scheduling, task allocation and random decision [24–28]. Glazebrook proposed a transformed index which is used in procedures for policy evaluation [29].Then,Glazebrook considered the optimal use of information in shooting at a collection of targets,generally with the object of maximizing the average number of targets killed[30,31]. In [1,7], we presented a work for the modeling,performance simulation, and channels optimal allocation of the layered BMDM/M/Nqueueing systems; and in[2],a mathematical model and method for BMD interceptor resource planning was presented.

All the literature mentioned above have provided some inspiration for this thesis.In the process of missile defense engagement,the probabilities of using EXOHI and ENOLI are different,and the probabilities that EXOHI and ENOLI kill a BM are different.Similarly, since the types of BMs are different,their penetration probabilities and threat values are different. The TLMD system always attaches a threat value to every BM it faces which could, for example,reflect the damage which would be caused should that BM penetrate its defenses[31–33].The value of threat to the defense area may vary according to the targets TLMD chooses, that is, the threat value of BMs will be dynamically changed after TLMD obtains more specific target information or knows that the target is intercepted.Thus,we take TLMD’s goal to be maximizing the expected return of BMs killed before the system demises and minimizing the cost of BMs leakage, and then the improved index policy is applied to the TLMD system. This paper is organized as follows.Section 2 proposes a general model for TLMD shooting decision processes. Section 3 illustrates the precise statements and proofs of the index shooting policy for the TLMD system.Section 4 is the discussion and expansion. Section 5 provides other shooting policies for comparison.Section 6 provides numerical examples.

2.General model for TLMD shooting decision-making

Nash originally put forward a kind of Markov decision theory in which at each decision epoch the decision-maker must choose one of theNarms [34]. Subsequently, this theory was further studied and developed by Fay, Glazebrook,Crosbie,Dumitriu,Katta and others[35–39].Now,we consider the case of shoot-look-shoot,a missile defense(MD)shooter has to plan a series of engagements with a finite fixed collection ofNBMs.Define“one engagement”at least including one shot of the MD system(during which the MD system or defense area may be destroyed by BMs penetration),and one look of targets intercepting results.It is assumed that the number of interceptors is not limited;then, the main decision-making problem of the shooting optimization is how to choose the next BM target which needs to be shot according to the previous shooting process and results, thus maximizing the expected return of BMs killed or minimizing the cost of BMs penetration.The shooting engagements can be described as the following discounted reward Markov decision process:

The state space of the BMs at timet ∈N isX(t)={X1(t),X2(t),...,XN(t)},whereXj(t)denotes the state of BMj(1 ≤j≤N). LetΩjbe the cognitive space(countable)of the TLMD system for all possible states of BMj,then

whereXj(t) =ωjdenotes that by timet, the TLMD system or defense area is destroyed when shooting BMj.XN+1(t) = 0 indicates that TLMD chooses to withdraw from engagement or be destroyed at timet;otherwiseXN+1(t)=1,that is,

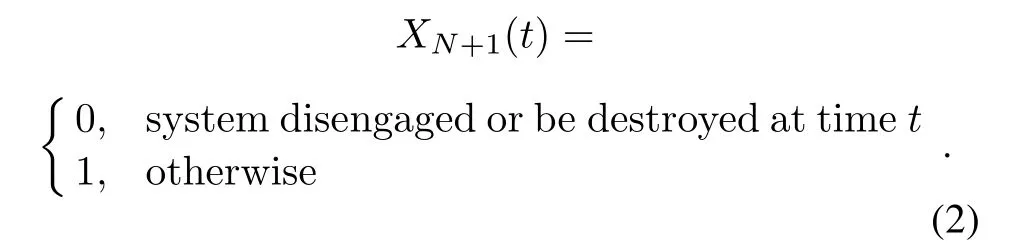
Obviously we haveXN+1(0) = 1. At eacht ∈N, ifandXN+1(t) = 1 are satisfied, then TLMD must choose to shoot,so that letajrepresent the action of shooting BMjin the TLMD (t+1)th engagement, andaN+1means that TLMD will no longer proceed with subsequent shooting operations.The expected return achieved by the TLMD system takes actionajatt ∈N is

whereRj:Ωj →R+(bounded and non-negative)may reflect the damage caused by a still alive BM’s penetration or its threat value to the defense area. The discount rateβ ∈(0,1)is usually a constant,which is used to simplify the loss of the expected return under certain subjective and objective factors.FunctionQjis represented as

Qj(x) indicates that if the TLMD system or its protected area is destroyed,the return of the shooting is 0;similarly,the return of stop shooting when there is no shooting opportunity for the BM is 0[40,41].That is,no returns are gained beyond time

If the system executes actionajatt,the probability that BM changes fromXj(t) to stateXj(t+1)can be determined by Markov lawPj

Note that the state spaceΩjshould contain the stateωj(BMjis killed),so bothandωjare the absorption states underPj,that is,to take any shooting action,all states are transferred to their own states with a probability of 1.

In order to describe the expected return of shooting actions,now we define bounded functions

3.Index shooting policy for the TLMD system

A policy for the TLMD system is actually a rule based on historical shooting effects to decide the next shooting action.If the shooting policy is represented byv,v(t)means that the action is taken att ∈N.Based on(6),the expected return of the total shooting process under the strategyvcan be expressed as

The purpose of this study is to find the optimal shooting policyv*, which can maximize the expected return. The model in Section 1 is a Markov decision model, which is called the generalized bandits decision process.The generalized bandits problem is a type of MAB problem in which the return is independent between different bandits. The multiplicatively separable form of the objective means that it can be used as the framework for the index shooting processes. From [41], we know that there exists an optimal policy for generalized bandits problems.LetXj(t)be the state of BMj(1 ≤j≤N)att,τis the stopping time of the shooting process,suppose that att=0 BMjis in statedenotes expected returns during[0,τ),then

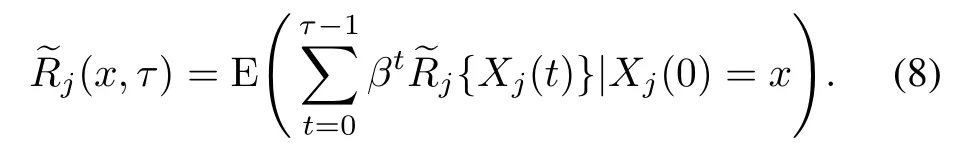
When the TLMD system or its protected area is destroyed, its shooting returns immediately terminate, and the indexis defined as

where 1-E(βτQj{Xj(τ)}|Xj(0) =x)is the probability that the TLMD system or its protected area will be destroyed by BMs during[0,τ),so(9)can be understood as

the indexGj(x) takes the maximum value forthat is,

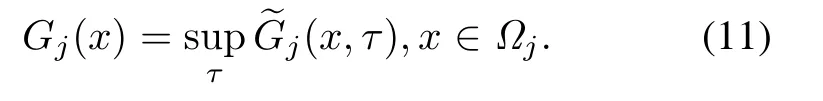
From (11)we can see that the index shooting policy is a strategy that can effectively balance the shooting returns and the risk that defense mission fails, and the goal is to maximize the return obtained from BMs killed before the system demises.

where 1 ≤b≤B,0 ≤x≤n,xindicates the number of shots organized by the EXOHI system in allnshots.We already know that the probability that the BM changes from stateXj(t)to stateXj(t+1)can be determined by Markov lawPj, since the type of BM is unknown,the calculation of(12)needs to be divided into four situations.

Situation 1Neither the TLMD system nor BMjis killed and the BM remains in the conflict, and the system will still need to continue to shoot,then

Situation 2BMjis killed.The system or its protected area is not destroyed.It is considered as follows:

(i)BMjis killed by the EXOHI system,then

(ii)BMjis killed by the ENOLI system,then

Situation 3The system(or its protected area)is destroyed.It is considered as follows:

(i)The EXOHI system is destroyed,then

(ii)The ENOLI system is destroyed,then

Situation 4Neither the system nor BMjis killed(due to guidance error,interference or other reasons,BMjfails to destroy its target),then

wherexis the number of shots organized by the EXOHI system,andn-xis the number of shots organized by the ENOLI system.

The expected return gained from BMjkilled in the engagement in four situations (without discount rate) above is given by

(i)BMjis successfully intercepted by the EXOHI system,then

(ii)BMjis successfully intercepted by the ENOLI system,then

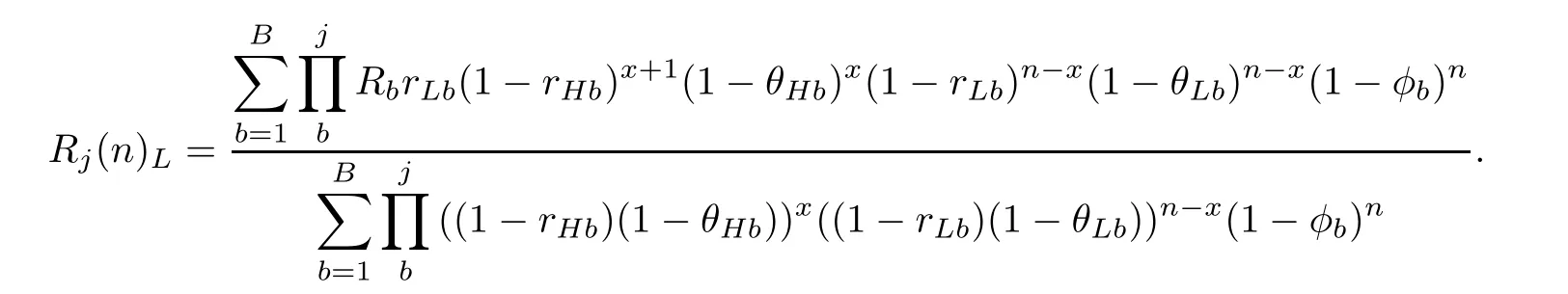
The above analysis assumes that the EXOHI system hasxshots, and the ENOLI system hasn- xshots. Ifnis unknown,ξHbcan be used as the probability that the decisionmaker uses the EXOHI system to intercept the BM,thenξLb=1-ξHbis the probability of using the ENOLI system to intercept the BM,then we have

wheren ∈N.The probabilityξHbandξLbare introduced in(13),soxcan be replaced byn·ξHb.This replacement is not absolutely necessary.If we can accurately know the number of predetermined shots of EXOHI and ENOLI systems for the BMj, it is not necessary to replace it; if we cannot know,we can set the probability of using different systems to intercept the target according to the conflict process. In order to enhance the generality of the model, we replacexwith the probabilityξHb.

It is known by (9) that the shooting process also requires a stopping timeτr,in whichris a positive integer,andXj(0) =n.τrindicates that after the system continuesrshots for the BMj, the system will stop shooting after one of the two is destroyed.Thenandare

We express our conclusion in Theorem 1.

Theorem 1There exist functionsGj:Ωj →R+such that,while the TLMD system or its protected area remains alive, that is,, then the system optimally engages BMj*if

wheren ∈N+,1 ≤j≤N,r≥1,1 ≤b≤B.

4.Discussion and expansion

According to Theorem 1, the optimal shooting policy is to shoot the BM with the maximum index until the BM is successfully intercepted.For the sake of understanding,we letr=1,then

is a “one-step index” defined by[41],Hj(n) can be understood as a one-step index for shootingbtype BMs,which is denoted by

The BM type in(18)follows a posteriori probability distribution, and the value ofHj(n) is closely related to the value ofRb,ξHb,rHb,rLb,θHb,θLbandφb. Table 1 lists several important correlation conclusions.

Table 1 Relationship between Hj(n) and Rb, ξH b, rH b, rLb,θH b,θLb,φb

Table 1 lists only a few correlation conclusions. There are seven variables in (18). The increase or decrease of a single variable does not necessarily lead to the increase or decrease ofHj(n), so we still need to calculate to determine the change ofHj(n). The probabilityθHb,θLbandrHb,rLbare not the opposite of each other in this paper,and there is no absolute correlation between them.For example,θHb,θLbmay be reduced with measures such as electronic interference,camouflage protection and others.φbdenotes the probability that thebtype BM penetrates successfully,but due to the fact that its own guidance error,interference or other reasons fail to destroy the protection area,in general,φbcan be a constant.Now we analyze the boundary conditions, if the functionHj(n) is monotonically decreasing, the maximum value of (17) is obtained for allnwhenr= 1, and at this timeGj(n) =Hj(n).This boundary condition indicates that the optimal shooting policy of the system is always selecting the BM with the highest index to shoot.If the functionHj(n)monotonically increases,then for alln,whenr →∞(17)gets the maximum value,

Whenr →∞, this boundary condition indicates that the optimal shooting policy of the system is to shoot continuously at each BM until the BM is successfully intercepted or the system is destroyed. If there are only two types of targets, that is,B= 2, thenHj(n) must be a monotone function,so we have Lemma 1.

Lemma 1For alln,the functionHj(n)must be monotonically increasing or decreasing whenB=2.

ProofIfB=2,then

since the value ofHj(n)/Hj(n+1) does not depend onjorn,thenHj(n) ≥Hj(n+1)orHj(n) ≤Hj(n+1)for allj, that is,Hj(n) is a monotonically increasing or decreasing function. □

Lemma 1 shows that when there are two BM types,the optimal shooting policy is one of the following two policies. (i) The system always shifts from shooting type 1 BMs to type 2 BMs or from shooting type 2 BMs to type 1 BMs, that is the system shooting the BMs(which are still alive) in a numerical order. (ii) The system keeps shooting on each type of BMs until the BMs are successfully intercepted or the system is destroyed.The motivation for this behavior comes from an index increase or decrease,which considers the type 1 BMs or type 2 BMs which have a higher shooting index.

5.Other shooting policies

In order to compare with the TLMD index shooting policy proposed in this paper,we give three other shooting policies for the system, which are the myopic policy,random policy and round-robin policy[41–46].

(i)Myopic policy

The myopic policy, which maximizes only immediate throughput, has been established as a simple and robust opportunistic spectrum access policy. If the principle of selecting shooting BMs by the index policy is to maximize the long-term return of shooting, then the principle of the myopic policy is to maximize the immediate return of shooting,that is,the myopic policy guides decisionmakers to shoot next at whichever BM is still alive and offers the decisionmaker the highest expected one-stage return.If the BMjbelongs to thebtype with a prior probability of

The myopic policy is not absolutely the optimal shooting policy. Suppose two interceptors intercept two BMs,the killing probabilities are 1, 0.9 and 0.9, 0 respectively andR1=R2= 1. If the myopic policy is adopted, the first interceptor should be used to intercept BM 1,and the second interceptor will not be used, with a total return of 1.If the index policy is used,the second interceptor should be used to intercept BM 1.If the interception fails,then the first interceptor is used to intercept BM 1 or BM 2,and the total return is 0.9×(1+0.9)+0.1×(0 +1) = 1.81.Thus the myopic policy is not the optimal policy.The myopic policy is aimed at the maximum return of shooting at the present time,with relatively small calculation and high demand for real time BM data, but it does not consider the effect of subsequent shooting and the probability of the TLMD system being destroyed,so it is suitable for shooting the identical BMs.Compared with the index policy,the myopic policy can be called a sub-optimal policy.

It can be seen that for each type of BM, when the BM threat value is an invariant constant,the myopic policy always chooses the most easily killed BM (rHborrLbis relatively large)to intercept,and obviously can maximize the number of BM killing.

(ii)Exhaustive policy

Here the TLMD system adopts the exhaustive shooting policy among those in which it shoots continuously at each BM until either party to the engagement is killed.This kind of shooting policy requires a simple sorting of the BM.For example,after the threat ranking of the BM,the BM can be shot in sequence from a lange to a small target threat value,that is, shoot at BMs in the order of descending values of the threats:

(iii)Round-robin policy

In special situations, the system may make irrational shooting decisions, such as round-robin shooting,if there is a lack of external BM indication information or strong electronic interference measures.Round-robin is one of the policies employed by process and decisionmakers in computing.The name of the policy comes from the round-robin principle known from other fields,where each person takes an equal share of something in turn.The round-robin policy is simple, easy to implement,and starvation-free.The round-robin policy is to shoot the surviving targets in a certain order, such as the target number from small to large,the threat value from large to small, and so on. The first BM is chosen at random.

6.Numerical examples

In this section, we give examples to verify the optimality of the TLMD index shooting policy. Considering the interception of ten BMs(N= 10),there are five BM types(B= 5),and the discount rateβ= 0.95.The parameters of the two examples are shown in Table 2. As shown in Table 2,the higher the BM threat value is, the more difficult the BM is to be killed,the higher the probability of the TLMD system or its protected area will be destroyed.

Table 2 Numerical example parameters setting

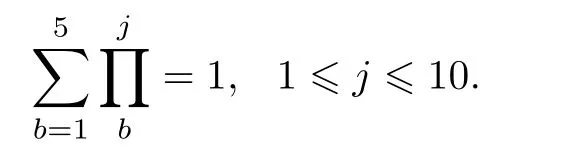
To simplify the calculation, we letRd= 0, indicating that the TLMD system does not stop shooting when the BM is alive and the system is not destroyed.φb= 0(1 ≤b≤5)indicates that if the interception of thebtype BM fails, the penetration of the BM will destroy the system.Table 3 is the data summary of shooting returns, Table 4 is the data summary of the number of BMs killed, and Fig.1 and Fig.2 are comparisons of shooting returns and the mean number of BMs killed.In general,it is believed that a better shooting policy is based on the immediate states of the BM and defense system,and it should be the immediate optimal policy(myopic policy);the exhaustive and round-robin policies are poor,because these two policies do not take into account the return too much.In fact,the two examples show that the index policy is better than the other three shooting policies, especially the mean returns and the mean killing BM number,which is in agreement with the conclusions of Theorem 1.

Table 3 Data summary of shooting returns

Table 4 Data summary of the number of BMs killed

Fig. 1 Comparison of returns and the number of BMs killed (Example 1)

Fig. 2 Comparison of returns and the number of BMs killed (Example 2)

Problems involving allocating limited resources in a limited time-frame under uncertainty may closely resemble the proposed shooting process. These problems could be non-defense related.

7.Conclusions

In order to cope with the increasing threat of BM in a shorter reaction time, a well-designed shooting policy should be done.A class of decision processes called MAB has been previously deployed to develop optimal policies for decisionmakers who attach a Gittins index to each target and optimally shoot next at the target with the largest index value. Unfortunately,for missile defense problems,the index policies are in general not proposed. The goal of this paper is to find a policy for shooting decisionmaking in TLMD interceptors planning. Our numerical results show that the index policy is better than a range of competitors, especially the mean returns and the mean killing BM number.Specifically,problems involving allocating limited resources in a limited time-frame under uncertainty may closely resemble the proposed index shooting process. We believe that the methodology can be applied to other non-defense related problems.