Carrier frequency and symbol rate estimation based on cyclic spectrum

CAO Sisi and ZHANG Weiyan

Institute of Computer Applications,China Academy of Engineering Physics,Mianyang 621000,China

Abstract: Carrier frequency and symbol rate estimation are the main contents of parameter estimation,which is the basis of modulation recognition and further processing of signals especially in non-cooperative communication.With the development of wireless communication, the signal transmission environment has become increasingly bad,causing more difficulties in parameter estimation.It is well known that the signal cycle spectrum is robust to noises and signal parameters are closely related. In practice, it is impossible to calculate the cyclic spectrum of infinite length data signals.When using finite length data to obtain a cycle spectrum,the truncation noise is induced, resulting in interference. It is necessary to overcome the influence of noises in order to improve the detection ability of discrete spectral lines. An improved method of the discrete spectral line extraction algorithm is proposed by reflecting the amplitude advantage of discrete spectral lines through salient features of continuous noises in discrete spectral line neighborhood.

Keywords: digital modulation signal, carrier frequency, symbol rate,cyclic spectrum,noise control.

1.Introduction

Automatic modulation identification and parameter estimation of digital communication signals are the key technologies in communication systems. This process is between signal detection and demodulation, and is of great significance in the fields of cooperative and noncooperative communication such as radio spectrum management and electronic warfare [1–8]. In communication systems, with the effect of modulation and transmission channels, the received signal ineluctably has some distortion. If the receiver wants to monitor, intercept and further process the signals to obtain communication content under unknown conditions, it is necessary to demodulate the signals. The parameters estimation including carrier frequency and symbol rate is the basis of modulation recognition and demodulation. In recent years, with the rapid development of modern communication and signal processing technologies, more sophisticated signal detection parameter estimation/modulation identification algorithms have been proposed to detect the existence of the target signal as well as obtaining important characteristics of the target signal[9–15].

Studies have been made by researchers on accurate parameter estimation. At present, carrier frequency estimation algorithms can be divided into the following three categories, time-domain, frequency-domain and spectraldomain. The first one is time-domain, such as the zerocrossing method.This method is greatly affected by noises,so the practical application is limited[16].Secondly,algorithms based on the discrete Fourier transform(DFT) are widely used to estimate carrier frequency.In[17],the idea of the frequency domain estimation algorithm is searching the peak of the spectral peak position, and a novel estimation method based on self-correlation for quadrature phase shift keying (QPSK) signal was proposed. At first, self-correlation biquadratic QPSK signal was analyzed,and then its carrier frequency was estimated through the modified rife (M-rife)algorithm instead of estimating frequency only by the max frequency line position. The simulation results indicate that our carrier frequency estimation method is feasible and more accurate than the former method,and the root of mean square error(RMSE)of the modified method is close to Cramer-Rao lower bound(CRLB).Zaplata et al.[18]introduced a novel approach to the frequency estimation suited for weak suppressed carrier binary phase shift keying(BPSK) signals even below the noise level. The variance of the spectrum averaging frequency estimator and the maximum likelihood (ML)estimator are presented. It is found that the variance of the spectrum averaging frequency estimator is worse compared to the ML estimator above about –3 dB of bit energy to noise level ratio. However, in very noisy environment the proposed algorithm keeps the variance lower in [18].Thirdly,it is well known that signal cycle spectrum is robust to noises and the signal parameters which are closely related[19].In[20],a novel algorithm was proposed to improve the accuracy in frequency estimation by transforming the character of cyclic autocorrelation correlation to the frequency domain to highlight the effective signal spectral,and tune the effective carrier frequency spectrum.In[21],a novel method of estimating carrier frequency and chip rate in severe signal environments was presented,based on the characteristics of cyclostationarity of multiple phase shift keying(MPSK)signals and the spectral lines on the bifrequency surface.This method,with a high estimating accuracy,has been proved by computer simulations.

About the symbol rate estimation, Liu et al. [22] proposed two approaches to the estimate symbol rate for multi-channel digital modulation signals mixed linearly,namely wavelet transform (WT) and twice WT. In [22],WT and twice WT were utilized in multi-channel linearly mixed signals after frequency conversion,respectively,to detect the jump border of mixed signals. Then we take Fourier transform to coefficients of WT. Symbol rate information can be extracted from spectrum of WT coefficients. Computer simulations are performed for common digital modulation signals. Communication signal cyclic spectrum density cyclic frequency domain contains a carrier frequency,symbol rate and other modulation parameter information,for stationary noise and interference have a good inhibitory effect[23–25].

The research is motivated by previous studies [24,25]in which we propose a new approach based on the cyclic spectrum and modified discrete spectral line extraction to estimate the modulation parameters. The paper is organized as follows. Section 2 gives the signal model. Section 3 explains the signal parameter estimation by the cyclic spectrum.Section 4 presents the simulation results and analysis.Finally,Section 5 is the conclusion.

2.Signal model and theory of cyclic spectrum

2.1 Signal model

The received signal can be defined as

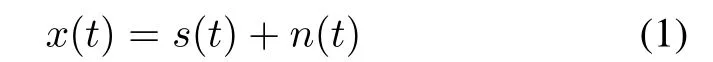
wheres(t)can be amplitude modulation(AM),MPSK or orthogonal frequency division multiplexing (OFDM) signals, andn(t) is the additive zero-mean Gaussian noise.s(t)can be expressed as

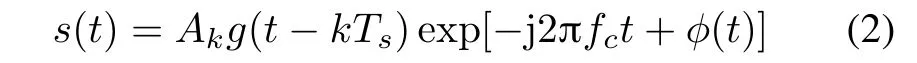
whereAkis the signal amplitude;g(t) is the pulse shape function;Tsis the symbol period;fcis the unknown carrier frequency;φ(t)is the signal phase.

After modulation, shaping filter and sampling, statistical characteristics of digital signals typically have a certain periodicity,called cyclostationarity[26].

2.2 Theory of cyclic spectrum

It is well known that most of communication signals are cyclostationary, and cyclostationary features can be used in signal detection [27], parameter estimation and modulation detection. The cyclic spectrum theory is depicted simply below.

x(t) is a complex sinusoidal signal with the mean zero and random noisen(t). The cyclic autocorrelation of a complex-valued time seriesx(t)is defined by

whereRx(t,τ) is the autocorrelation function ofx(t). Ifx(t+τ/2)x*(t-τ/2) has statistical properties, and the period isT0.Then

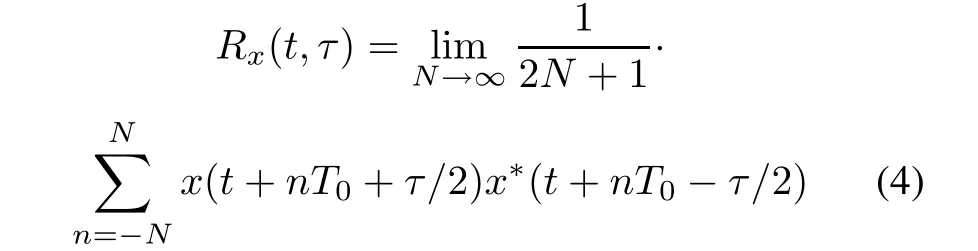
where 1/T0is the symbol rate.Do its Fourier series expansion as

whereα=m/T0.After Fourier transform,

whereis called the cyclic spectrum density function,αis the cyclic frequency andfis the fourier frequency.

3.Parameter estimation based on cyclic spectrum

Since stationary noise does not have cyclostationarity in the case where cyclic frequency is not equal to zero, and the theoretical spectrum correlation function is zero [28].The use of cyclic spectrum correlation in signal analysis and processing can eliminate some random factors coming from the signal itself,such as additive white Gaussian noise.Therefore,in terms of parameter estimation and extraction it shows better anti-interference and high resolution. The cyclic spectral magnitude can be obtained approximately atαsection inf= 0 andf=fcfor all signals [29]. The following description is given as an example of MPSK.

3.1 Correspondence between parameter and cyclic spectrum

The MPSK modulation signal model can be expressed as

wherex1(t)is the complex envelope ofx(t),fcis the carrier frequency,ϕ0is the initial phase of the signal,Tis the duration of a symbol, andq(t) is the pulse shaping filter.θn ∈{2π(m-1)/M}(m=1,2,...,M).

The general forms of the MPSK signal cyclic spectrum are shown in(9),(10),Fig.1 and Fig.2.

WhenM=2,

WhenM≥4,

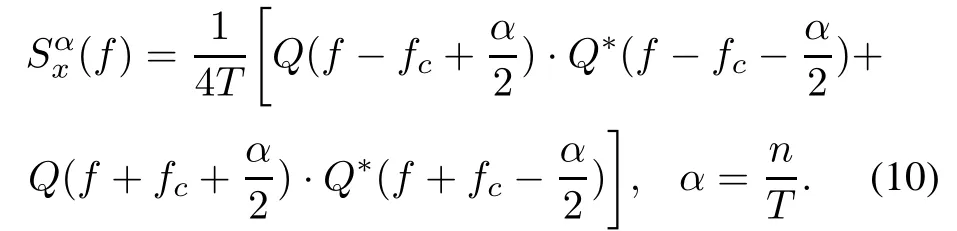
Wherein,Q(f) is the Fourier transform of the shaping pulseq(t). Analyzing the cyclic spectrum magnitude through(9)and(10)for all MPSK signals can acquire two important expressions.

Fig.1 Cyclic spectrum of BPSK signals

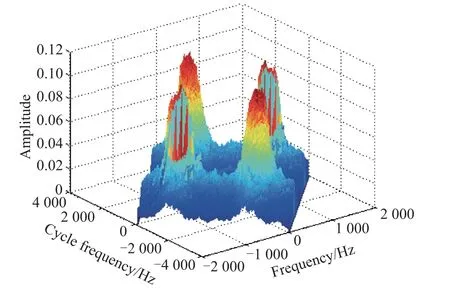
Fig.2 Cyclic spectrum of QPSK signals

f-section of the cyclic spectrum whenα=0 is

Due to the characteristic ofQ(f),there is a peak value atf=±fc.

α-section of the cyclic spectrum whenf=0 is

The first item is to be close to a small value of 0. In the second item, the cyclic spectrum has a peak value whenα=±2fc, and the second largest value whenα=±2fc+1/T.For the cyclostationarity of white Gaussian noise,the noise cyclic spectrum is not included here,so we search the maximum value whenf= 0, as shown in Fig.3.At this point the search to a maximum value corresponding to the cycle frequency,in theory,equals twice the carrier frequency.

Fig.3 α-section of BPSK/QPSK signal cycle spectra when f =0

α-section of the cyclic spectrum whenf=fcis

The first item is close to a small value of 0. In the second item, the cyclic spectrum has a peak value whenα=±1/T,and the second largest value whenα=±1/T.Thus,we search the maximum value whenf=fc.At this point the search to a maximum value corresponds to the symbol rate.

We can make use of these properties to calculate the carrier frequency and the symbol rate.The following conclusions can be drawn.

(i) The cyclic spectrum is a two-dimensional transformation,and the two parameters are spectrum frequencyαand frequencyf[30].

(ii) Theα-section of the cyclic spectrum whenf= 0 has a maximum value atα=±2fc.

(iii)Theα-section of the cyclic spectrum whenf=fchas a maximum value atα=±1/T.

3.2 Improved discrete spectral lines algorithm

The above is an ideal infinite loop spectral characteristics in the case of the MPSK signal sequence, when the limited observational data length,interference term signal and noise will affect the spectral characteristics of the MPSK signal cycle spectrum.

In order to reduce the influence of truncated noises, an estimation method based on the discrete spectral line is given by the cyclic spectrum[31].The cyclic spectrum of signals is a nonlinear transformation.The cyclic spectrum not only reflects the spectrum features of symbol rate information,but also truncates the noises,affecting the extraction of spectrum features.This effect is evident especially when the data length is limited.The extraction method of discrete spectral lines is promoted in the paper,which can suppress truncation noises, improve estimation accuracy and reduce estimation variance.

The significant difference between discrete spectral lines and lines on both sides of adjacent amplitudes is shown in Fig. 4, indicating that the background noise amplitude difference between adjacent locations is small.Therefore, it is applicable to make full use of the salient features of the projection of discrete frequency components in their neighborhoods,which is different from continuous noise, to estimate the carrier frequency and the symbol rate.The influence of truncation noises needs to be suppressed in order to improve the anti-jamming ability of noises and improve the accuracy.An improved move average compare(MAC)discrete spectrum line extraction algorithm is proposed in the paper,which is able to improve the detecting ability of discrete spectrum lines and overcome the influence caused by noises. In order to reflect the corresponding improvement of the amplitude value of discrete lines in the algorithm,we replace the original amplitude with the ratio of the square of the amplitudea(i)and take lengthLbefore and after that point of the neighborhood. Then the weighted average of the amplitude is expressed by the following formula:

wherec(n) = 1/(n - i+L+ 1). Since the uncorrelated noise is suppressed after the improved discrete spectral lines algorithm,the relevant frequency and symbol rate information will be highlighted.

Fig.4 α-section of BPSK/QPSK signal cyclic spectra when f =fc

The simulation diagram of the BPSK signal below is under the condition that the signal to noise ratio(SNR) is 5 dB, Fig. 5(b) is obtained by direct MAC with an improved operation.Fig. 5 clearly shows that the frequency components of Fig.5(b)is more obvious(the symbol rate information), making it easier to search the peak. For Fig.5(a),some of the components caused by noises will be treated as a peak,resulting error estimation of the symbol rate,reflecting the advantages of the above data processing.

Fig.5 α-section of BPSK signal cycle spectra when f =fc

3.3 Parameters estimation value obtaining

Step 1The cyclic spectrum of the received signal is calculated by the observation data.

Step 2According to the cyclic spectrum, theαcross section ofis intercepted, the cross section is optimized, the maximum value is searched and the position of the frequency is recorded asandThe carrier frequency estimation formula is

Step 3According to the theoretical analysis,the nonstationary signal has a value only whenα=0,and the rest results are zero.Therefore,we intercept theαcross section ofwhenf=fc, then optimize the intercept section ofα.Search the maximum value of the cross sectionLdmax1andLdmax2except the circulating frequency which is 0 Hz, and the symbol rate estimation formula is

4.Simulation results and analysis

Carrier frequency and sign rate estimation are influenced by SNR,modulation mode and data length,which are analyzed through experiments in this section.The simulation experiment is carried out to illustrate the effectiveness of the algorithm and verify the performance of the algorithm under the AWGN channel model. The normalized mean square error (NMSE) of the parameter estimation is the evaluation criterion in this paper.The formula for the normalized MSE is given below,where the true value for the carrier frequency isfcand the symbol rate isfd.fciandfdirepresent the value estimation of the carrier frequency and the symbol rate.

Simulation parameters: sampling ratefs= 24 000 Hz,carrier frequencyfc= 3 000 Hz, symbol ratefb=2 400 baud.The smoothing window length is 64 estimated by the frequency domain smoothing method.Five hundred independent Monte Carlo experiments are performed at different SNRs.

Experiment 1Simulate the normalized MSE of carrier frequency and symbol rate estimation for different modulation modes such as signal 2ASK,2FSK,BPSK and QPSK under different SNRs. The data length takesN= 5 120 sample points.

According to the previous theory, the discrete lines of the 2ASK signal and the 2FSK signal are the most obvious,so that carrier frequency estimation normalized MSE has been reduced to zero as the SNR is –4 dB.The carrier frequency estimation error of BPSK and QPSK signal can be reduced to zero in the SNR of –2 dB in Fig.6,and the NMSE of the symbol rate estimation of the 2ASK signal is not higher than 10-2at an SNR of 6 dB.

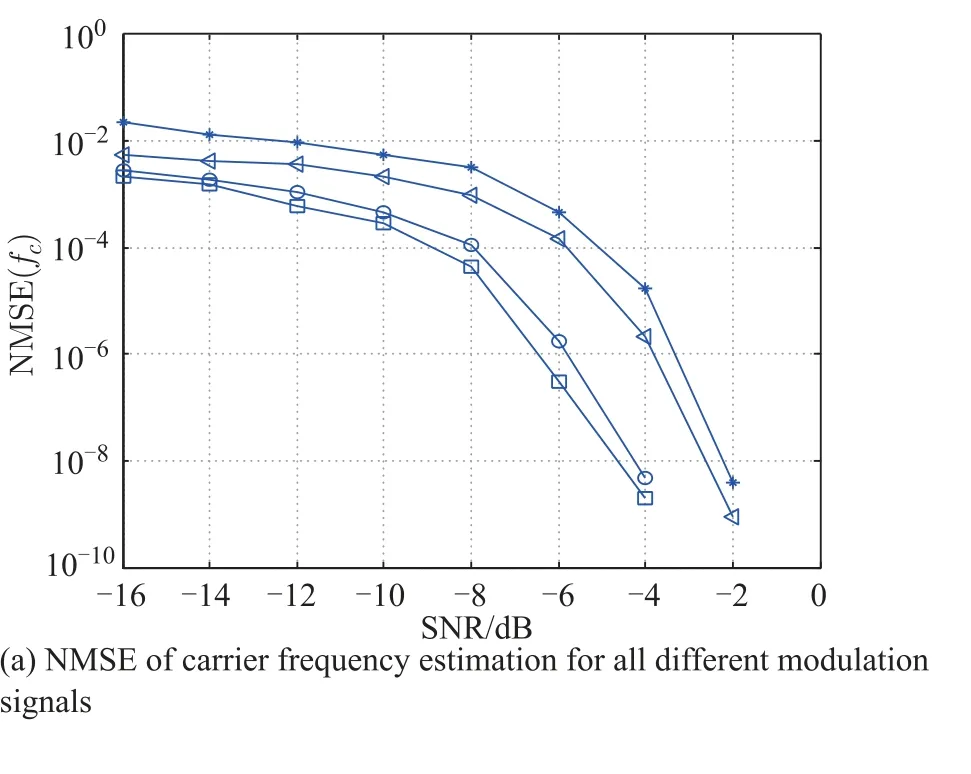
Fig.6 NMSE of carrier frequency and symbolic rate estimation for different modulation signals

The 2FSK signal is 4 dB.The NMSE of the BPSK signal is not higher than 10-3when the SNR is 6 dB,and the QPSK signal is 4 dB.

Experiment 2Compare the influence of different data lengths on the error of carrier frequency and symbol rate estimation. Data lengths are taken asN= 5 120, 8 000,12 000 for simulation.

It is shown in Fig.7 that the increase of data length can greatly improve the algorithm performance and reduce the MSE in parameter estimation.WhenN= 5 120,the carrier frequency is accurately estimated when SNR＞–2 dB and the symbol rate is accurately estimated when SNR＞6 dB;whenN=8 000,the carrier frequency is accurately estimated when SNR＞–4 dB and the symbol rate is accurately estimated when SNR＞4 dB; whenN= 12 000,the carrier frequency is accurately estimated when SNR＞–6 dB and symbol rate is accurately estimated when SNR＞2 dB. The longer the data length is, the better the performance of the algorithm will be.

Fig.7 NMSE of parameter estimation for different signal lengths of the modulated signal

The reason is that cyclic cumulants and cyclic spectrum essentially reflect the statistic features of signals,of which the anti-noise performance advances gradually. In practical treatment, calculation is made with limited length, in which the theoretical value is closer, the induced truncation noise is smaller,the accuracy of parameter estimation is higher and the MSE is smaller while the data length is longer.

Experiment 3Compare the performance of carrier frequency and symbol rate estimation by the cyclic spectrum algorithm and the improved algorithm in this paper.

The section of cyclic spectra is used to estimate the carrier frequency and symbol rate.As shown in Fig.8,BPSK1 represents the original algorithm, and BPSK2 represents the improved algorithm.The improved algorithm improves the estimation accuracy and reduces the NMSE. As the SNR grows,the estimation result gets better.Accurate estimation of symbol rate estimation is at SNR＞6 dB and carrier frequency estimation is at SNR＞-2 dB. Thus,the algorithm has a better anti-noise performance.This is because the additive Gaussian noise is stationary.The proposed algorithm is used to estimate the discrete spectrum of the carrier frequency and bit rate.The additive Gaussian noise at the spectral cross section is zero, thus effectively overcoming the effect of noises.For the background noise introduced by the data truncation,the improved MAC algorithm is used to enhance the discrete spectrum at the cyclic frequency, which overcomes the influence of the background noise.Thus, the overall anti-noise performance of the algorithm is the best.

Fig. 8 NMSE of carrier frequency and symbol rate estimation of BPSK signals

5.Conclusions

In this paper, the problem of parameter estimation in modulation recognition is studied. The estimation of the parameters mainly includes the carrier frequency estimation and the symbol rate estimation. Considering that the cyclic spectrum method has a good anti-noise performance and can be locally calculated, the carrier frequency and symbol rate can be estimated by different cross sections of the cyclic spectrum. In the process of line extraction,an improved discrete spectral line extraction algorithm is introduced.The simulation results show that the improved method has a better performance than the original method and improves the estimation performance.