含间隙铰链的非线性动力学建模及数值分析

徐 彦，王培栋，孙禄君，朱东方，方 琴

（1.浙江大学 航空航天学院，浙江 杭州 310027；2.上海航天控制技术研究所，上海 201109；3.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

由于机构运动副和其他设计需求，空间可展开机构铰链运动副中不可避免地存在铰链间隙［1］，导致空间可展开机构具有非光滑力学特征：1）铰链间的间隙使得机构的实际运动与理想运动之间出现偏差，在展开和振动过程中各构件之间不可避免地产生接触和分离；2）由于间隙的存在，使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍［2］；3）铰链中运动部件间的干摩擦也是引起可展机构非光滑特征的主要因素之一。间隙、碰撞和干摩擦等复杂非光滑因素使得空间可展开机构在展开过程及锁定后容易发生振动，锁定后在时变的空间热载荷作用下容易引发热致振动，直接影响航天器姿态运动以及有效载荷的指向稳定度，且这些因素往往难以完全有效控制。

由于铰链中存在间隙，在振动过程中铰链的运动副之间会发生相互接触和碰撞。碰撞分析模型主要有：1）经典瞬时冲击模型，碰撞过程被认为是瞬时完成的，根据恢复系数和动量守恒定理确定碰撞前后的瞬时速度关系［3-4］。该模型不必考虑碰撞力和时间的关系，计算效率较高。但是模型中的恢复系数依赖于实验，缺乏完备的理论支持，也不能描述碰撞力持续时间和作用过程。2）铰链的实体接触模型［5］，可充分地考虑复杂形状和局部变形，分析碰撞力的时间历程与空间分布规律［6］。但是由于处理接触过程的繁杂性和计算效率低等，在复杂结构分析中应用较少。3）连续接触碰撞力模型，包括Kelvin-Voigt 线性弹簧 阻尼模型［7］、Hertz 接触模型［8］、Hunt-Crossley 模 型、Lankarani-Nikravesh（LN）模型、改进L-N 模型、Bai 小间隙接触模型［9］等。这些模型简单方便，可以描述压缩和恢复过程，考虑了接触力的大小和接触碰撞的时间历程，但是各有适用条件。由于空间可展开机构大多工作在真空环境中，运动副清洁表面直接接触，在运动过程中产生干摩擦。摩擦分析模型分为静态摩擦模型和动态摩擦模型两类［10］。静态模型将摩擦力描述为相对速度的函数，而动态模型描述为相对速度和位移的函数。静态模型包括：库伦模型、静摩擦与库伦模型、Stribeck 模型、状态转换模型、Armstrong七参数模型等。动态模型包括：Dahl 模型、Bliman-Sorine 模型、Oden 模型、复位积分器模型、鬃毛模型、LuGre 模型［12］、Leuven 模型［11］等。对于间隙铰链中的摩擦，应采用动态模型。

现有的间隙铰链分析模型大多为二维模型，但是实际的间隙铰链均为三维结构，间隙铰链中不仅存在销轴径向接触碰撞，而且在销轴轴向也存在接触碰撞，销轴轴线和轴套轴线还存在夹角。针对典型的圆柱状铰链中发生轴向和侧向耦合碰撞的动力学特点，本文提出了更为合理的含间隙铰链分析模型，并将其应用于含间隙铰链桁架的动力学建模与仿真中。

1 含间隙铰链非线性动力学模型

1.1 “T”字型等效梁模型

含间隙铰链运动副包括销轴和轴套，实体模型如图1 所示，可将销轴简化为圆柱体，轴套内表面简化为圆柱面。接触碰撞力的作用点并不在销轴或轴套的轴线上，为了建立含间隙铰链分析模型，含间隙铰链可简化为如图2 所示的两个相互作用的“T”字型等效梁模型。图2中，等效梁模型中的梁12 代表销轴，梁45 代表轴套，点1、2 是销轴的端点，点3为销轴中点，点4、5 是轴套的端点，点6为轴套中点，销轴和轴套分别通过点7、8 和其他构件相连接。梁13、23、37、46、56、68 都用三维梁单元来离散建模。在该分析模型中，侧向、径向碰撞力都只能施加在销轴和轴套梁单元的节点上。

图1 含间隙铰链实体Fig.1 An entity with clearance joints

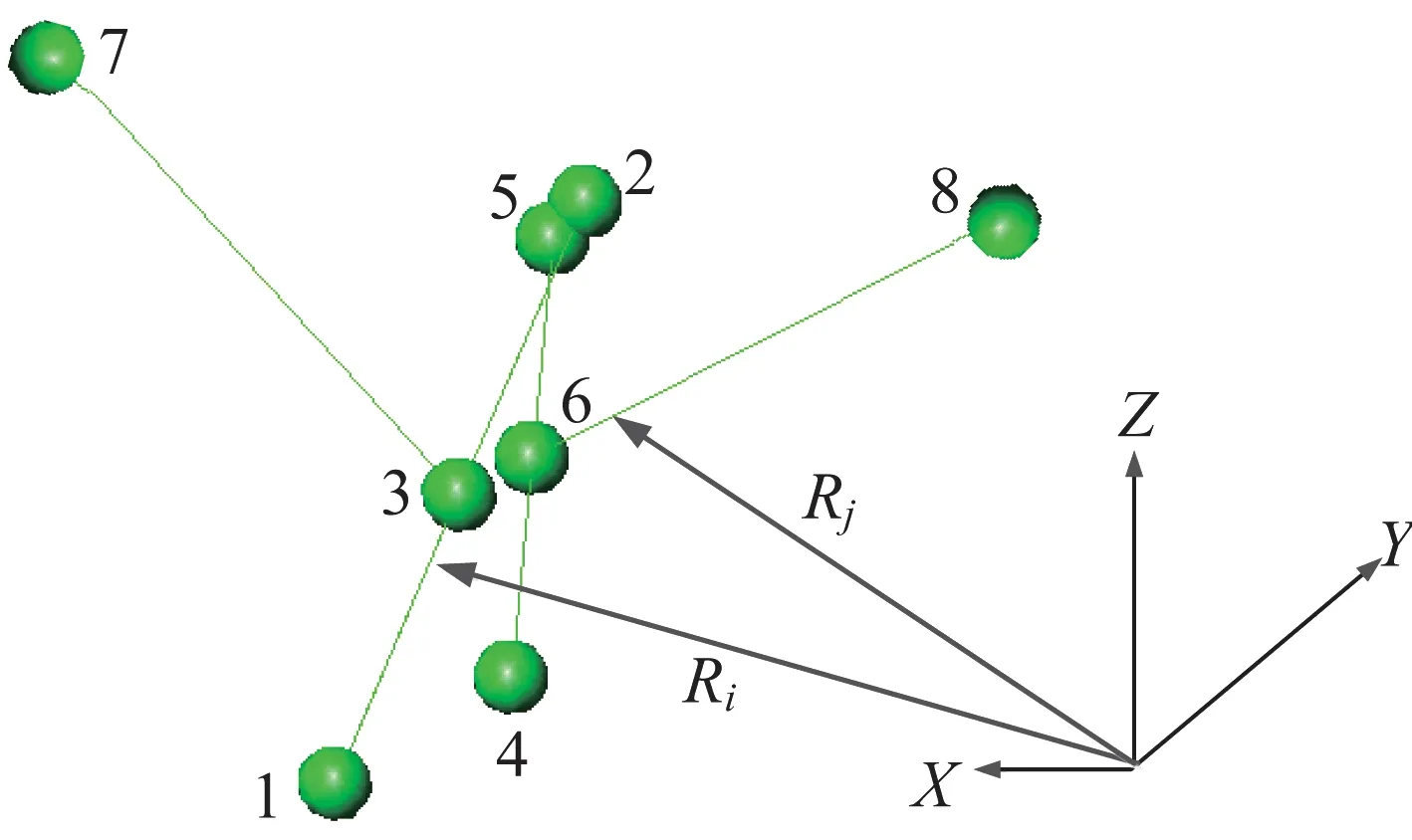
图2 “T”字型梁模型Fig.2 T-type beam model

理想的铰链中没有间隙，销轴和轴套只存在绕公共轴线的相对转动。对二维平面间隙铰链，销轴与轴套之间存在销轴径向的间隙。而实际含间隙铰链结构中同时存在侧向和径向间隙，如图3所示。当轴套与销轴挡块发生碰撞时，称为侧向碰撞（如图3（a）所示）；当轴套与销轴发生沿径向的碰撞时，称为径向碰撞（如图3（b）所示）。而且侧向和径向碰撞还可能同时发生，导致在运动过程中销轴和轴套的轴线并不重合，甚至两者可能不在同一个平面内。销轴和轴套的接触状态取决于该时刻两者的空间相对位置，而销轴和轴套分别与空间可展开机构的其他构件相连，故销轴和轴套的接触状态取决于各自所在的杆件的运动状态。为了分析铰节点中销轴和轴套的接触碰撞过程，需要判断销轴和轴套之间的接触碰撞状态和潜在接触点。

图3 侧向碰撞和径向碰撞Fig.3 Lateral collision and radial collision

1.2 三维间隙链动力学方程

本小节推导考虑含间隙铰链后的结构动力响应分析过程。如前所述，将含间隙铰链的实体模型图（如图1 所示）简化为如图2 所示的两个相互作用的“T”字型模型，销轴中心点的位矢为Ri，轴套中心点的位矢为Rj，其中，销轴中的节点编号为1、2、3、7，对应的轴套中节点为4、5、6、8。

模型中的杆13、23、37 和46、56、68 都用有限元法的欧拉梁单元来离散建模，可以得到一个“T”字型模型的结构动力学方程为

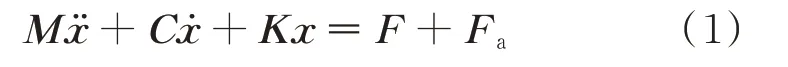
式中：M、C、K分别为不考虑铰链间隙时的结构质量矩阵、阻尼矩阵、刚度矩阵。

由梁单元相关矩阵集成得到广义位移矢量为

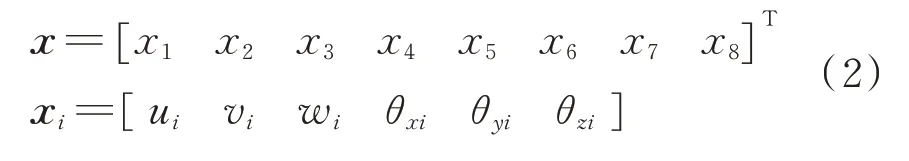
F为外载荷节点力矢量，Fa为附加的非线性铰链力矢量，可通过后续的含间隙铰链接触力分析模型得到。

式（1）即为含间隙铰链的动力学模型，可以方便地集成到总体结构的动力学方程中。采用相应的数值积分算法如Newmark 法，即可进行含间隙铰链结构的动力学响应分析。

2 含间隙铰链接触力分析模型

2.1 接触碰撞检测算法

如图1 所示的含间隙铰链，将销轴简化为圆柱体，轴套内表面简化为圆柱面，销轴和轴套在1 节点侧接触碰撞分析模型如图4 所示。销轴两端面圆心分别为点1 和2，点3为销轴轴线12 的中点。轴套两端面圆心分别为点4 和5。销轴中心点的绝对坐标为Ri，轴套中心点的绝对坐标为Rj。

图4 左侧接触碰撞分析模型Fig.4 Analysis model for the contact collision on the left side

推导径向碰撞的潜在碰撞点和最小距离，轴套端面圆周上的某一点与销轴圆柱外表面间的距离是轴套与销轴间的最小距离，且在同一时刻轴套的两个端面圆周都有可能与销轴发生接触，即潜在接触点必然位于轴套两端面的圆周上。图4中，已知销轴两端节点1、2、3 在绝对坐标系下的位矢分别为R1i、R2i、R3i，和轴套两端节点4、5 在绝对坐标系下的位矢分别为R4i、R5j。还已知销轴外径为Ri，轴套内径为rj，外半径为Rj。接下来分步骤说明：

步骤1确定切平面▱T1T'1。

如图4 所示，销轴轴线矢量r12=R2i−R1i，由轴套一端面圆心4 点向销轴轴线单位矢量作垂线，垂足记为4'，在矢量三角形△344'中有

其绝对坐标R4'为

则4 点和4'点的连接矢量为

其单位矢量为e44'。延长线44'与销轴圆柱体在4'处的横截面圆周相交于点T1，点T1的绝对坐标RT1为

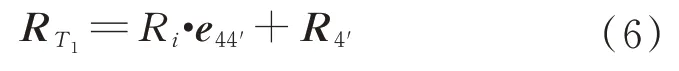
过点T1作销轴圆柱体外表面的切平面，记为YT1T'1，方程为

切平面中既垂直于44'，又垂直于销轴轴线矢量r12的一条直线矢量rT1T1'为

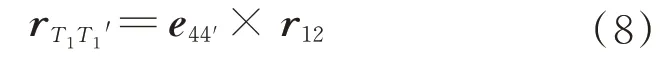
步骤2确定径向碰撞的潜在碰撞点。

过点4 作销轴切平面▱T1T'1的平行平面▱τ1，平面▱τ1中过点4 并和rT1T1'平行的直线为4Q1，线4Q1的矢量为r4Q1=rT1T1'。径向碰撞的潜在碰撞点位于和平面▱τ1平行的轴套切平面上，在以点4为圆心的轴套端面内圆周上，则线4-的矢量为

潜在碰撞点在线44'上的投影位于线44'的延长线，故如果 满足r4n′j1·e44'＞0，点的位矢即 可求得

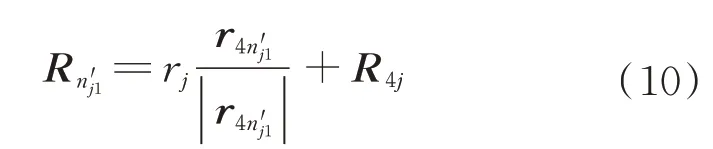
如果满足r4n′j1·e44'＜0，点的位矢为

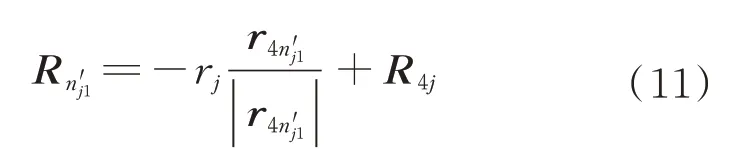
步骤3确定径向碰撞的间隙大小和方向。

如果轴套上点嵌入销轴，下式为负号；如果轴套和销轴处于分离状态，下式为正号。

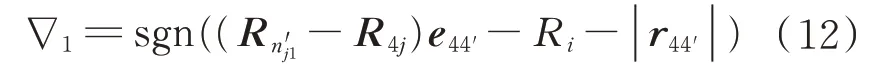
轴套和销轴在该端部的径向接触碰撞最小距离为

如果S1＜0 发生接触碰撞，该端部接触碰撞力在轴套上的作用点在点，在轴套上的作用点在点ni1，作用方向沿着44'矢量方向，销轴对轴套的非线性接触力作用方向e44'。整理上述公式得到轴套和销轴在该端部的径向接触碰撞最小距离为

式中的各项均为销轴、轴套的轴线矢量及截面尺寸，故径向接触碰撞最小距离为销轴、轴套的轴线节点绝对坐标及截面尺寸的函数。

步骤4确定侧向碰撞的潜在碰撞点。

接下来推导侧向碰撞的潜在碰撞点和最小距离，侧向碰撞发生在轴套外表面和销轴挡板之间。以点4为圆心的轴套端面和以点4'为圆心的销轴截面相交于过点4 的直线4P1，该直线分别和销轴、轴套轴线垂直，矢量4P1为

侧向碰撞的潜在碰撞点在以点4为圆心的轴套端面外圆周上，且距离销轴挡板最小，等效于距离以点4'为圆心的销轴截面最大。故线4-垂直于交线4P1，同时垂直于轴套轴线45，有

侧向碰撞的潜在碰撞点在轴线12 上的投影位于点4'的左侧，故如果满 足r4nj″1·e12＞0，点的位矢即可求得

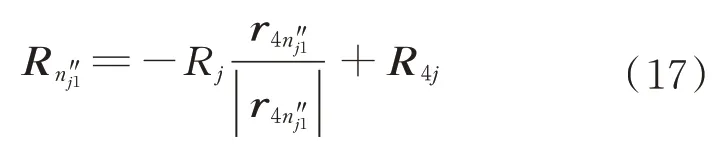
式中：Rj为轴套外半径。

潜在碰撞点在轴套上，对应的销轴上的潜在碰撞点绝对坐标为

步骤5确定侧向碰撞的间隙大小和方向。

记销轴轴线长度为Li=|r12|，点和点3 的连线矢量为销轴挡板平面的法矢即销轴轴线矢量r12，如果轴套上点嵌入销轴挡板平面，下式为负号；如果轴套和销轴挡板平面处于分离状态，下式为正号。

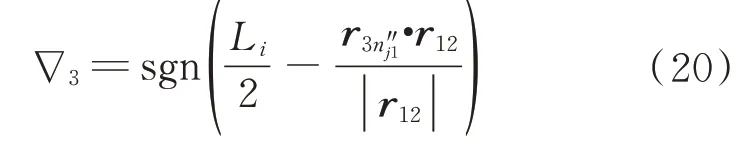
则轴套和销轴在该端部的侧向接触碰撞最小距离为

如果S3＜0 发生接触碰撞，该端部接触碰撞力在轴套上的作用点在点，在销轴挡板上的作用点在点，作用方向沿着销轴轴线方向，销轴对轴套的非线性接触力作用方向为e12。整理上述公式得到轴套和销轴在该端部的侧向接触碰撞最小距离为

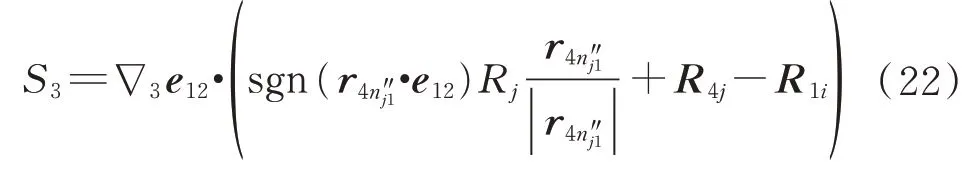
侧向接触碰撞最小距离也为销轴和轴套的轴线节点绝对坐标及截面尺寸的函数。

采用同样方法可以进行2 节点侧的潜在接触碰撞检测。

2.2 含间隙铰链接触力分析模型

含间隙铰链接触碰撞的类型按销轴和轴套轴线是否平行可分为两大类：如果销轴和轴套轴线平行，径向碰撞为线碰撞，侧向碰撞为面碰撞，其中线碰撞可简化为二维碰撞，按点碰撞处理；如果销轴和轴套轴线不平行，径向碰撞为点碰撞，侧向碰撞为点碰撞或者点-面斜碰撞。

2.2.1 点碰撞力分析

在图4中，接触碰撞对点ni和点的碰撞截面是过点ni的销轴截面，其受力状态按以下模型近似处理。根据间隙尺寸的不同，可以按以下两种碰撞力假设模型建模：小间隙的铰链径向非线性接触模型和大范围间隙的铰链径向非线性接触模型。

1）小间隙的铰链径向非线性接触模型。

对于小间隙接触碰撞，由于接触碰撞载荷的作用，将导致间隙铰轴与轴承间的接触面积增大，进一步将导致间隙铰轴与轴承的接触为协调接触。采用改进的非线性连续接触力模型来描述小间隙的铰链接触碰撞作用［9］，其表达式如下：

式中：δ为接触点穿透深度为相对碰撞速度；K为碰撞体的非线性刚度系数；ξ为改进的阻尼系数。式中右边第一项代表碰撞过程的弹性变形力，第二项为碰撞过程中的阻尼力项，则述了碰撞过程中的能量损失行为。在图4中，FN的作用方向沿着44'矢量方向。

碰撞体的非线性刚度系数为［13］

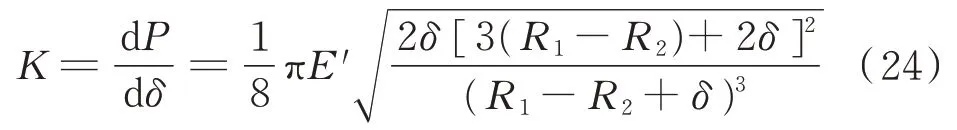
式中：R1、R2为接触对在接触点处的曲率半径，当小间隙时，销轴和轴套的轴线夹角不大，轴套和销轴的弹性变形较小，可以视为轴套和销轴的几何半径；E'为复合弹性模量。

改进的阻尼系数ξ为

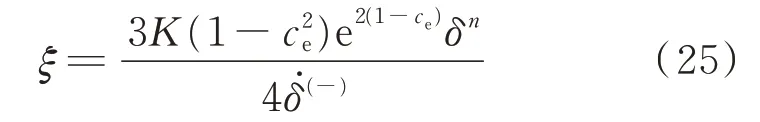
式中：ce为恢复系数为接触点的初始相对速度。该阻尼系数不受碰撞恢复系数的限制。

2）大范围间隙的铰链径向非线性接触模型。

协调接触模型和非协调接触模型中的大间隙和小间隙假设，限制了接触模型在不同间隙下的适用性。因此，为了建立更加精确的接触模型，需要从精确的接触深度和接触半角关系着手［15］。铰链中单耳板和销轴间隙接触时，铰链接触力和接触点穿透深度的关系为

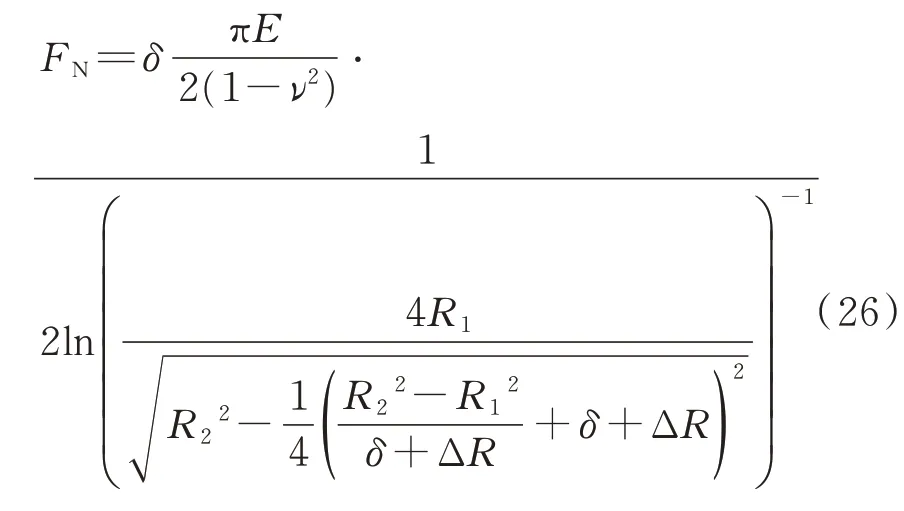
该接触碰撞模型的假设与接触体之间的间隙大小无关，适用于大范围间隙下的铰链接触。

2.2.2 摩擦模型

含间隙铰链存在干摩擦，Coulomb 摩擦模型是应用最为广泛的铰链间摩擦模型，其形式如下：

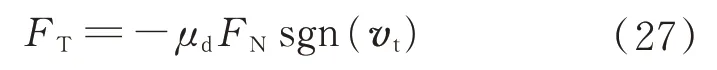
式中：μd为滑动摩擦系数；FN为法向接触力；vt为接触过程中的相对切向速度。摩擦力总是阻碍运动，与运动速度vt相反，其大小为常值。

运动副元素在切向接触时，相对运动速度较低时会出现粘滞等现象，并且在数值计算时摩擦力会随着速度方向的变化而突变。为了解决切向速度为零时摩擦力状态转换的问题，采用一种修正的Coulomb 摩擦力模型［14］，该模型中摩擦系数随切向滑动速度动态变化，摩擦力计算公式为

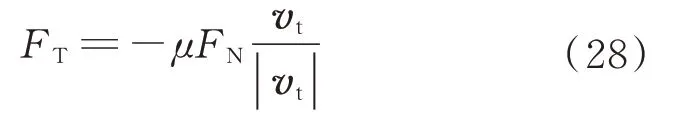
该模型中摩擦系数μ是滑动摩擦系数μd和动态修正系数cd的函数，μ=μdcd，

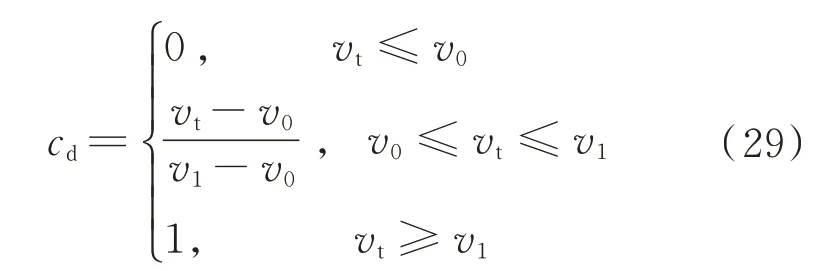
式中：v0、v1为给定的切向速度限值；vt=|vt|。

2.2.3 面碰撞力分析

当销轴和轴套的轴线平行（R12//R45）时，轴套和销轴侧板之间的接触类型为面接触，接触面域为圆环，面积为

接触碰撞力可表示为［16］

式中：Ej为轴套材料的弹性模量；Rj为轴套外半径；rj为内径；lj为轴套 长度。

3 非线性铰链力施加方法

3.1 点碰撞的等效施加

3.1.1 径向接触力的等效施加

如图5 所示，销轴和轴套在1 节点侧发生了径向碰撞，该端部接触碰撞力在轴套上的作用点在点，在轴套上的作用点在点ni1。销轴和轴套在建模时分别用杆单元12 和45代替，轴套45在接触点处受到的径向碰撞力FN1，销轴12在点ni1受到碰撞力FN1，径向碰撞力必位于点1、2、4所在的平面Y124内。

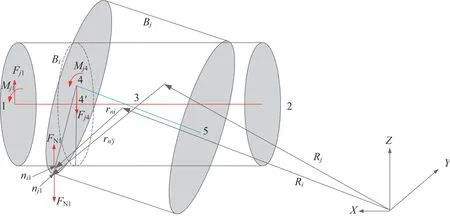
图5 径向接触力等效施加Fig.5 Equivalent application of the radial contact force

根据力的等效原理，在平面▱124 上，如果将轴套45 在点所受的碰撞力平移到点4，需要在点4上施加力Fj4，还需要同时施加如图5 所示的力矩Mj4：

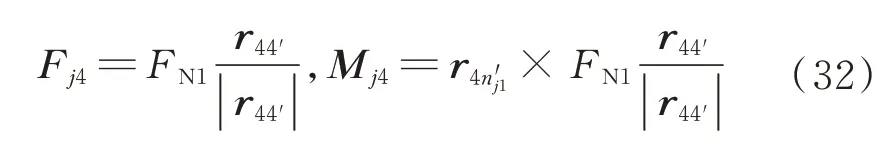
同样，将销轴在接触点ni受到的碰撞力进行等效平移到点1，需要同时施加如图5 所示的力Fi1和力矩Mi1：

3.1.2 侧向接触力的等效施加

如图6 所示，如果销轴和轴套在一端发生了侧向碰撞，考虑实际中轴套的壁厚，接触点为点销轴和轴套在建模时分别用杆单元12 和45 代替，轴套45 在接触点受到的侧向碰撞力FN3，销轴挡板在点点受到碰撞力FN3。

图6 侧向接触力等效施加Fig.6 Equivalent application of the lateral contact force

采用相同的等效方法，在平面▱124 上，将轴套45 在点所受的碰撞力平移到点4，需要在点4 上施加力Fj4，还需要同时施加如图6 所示的力矩Mj4：

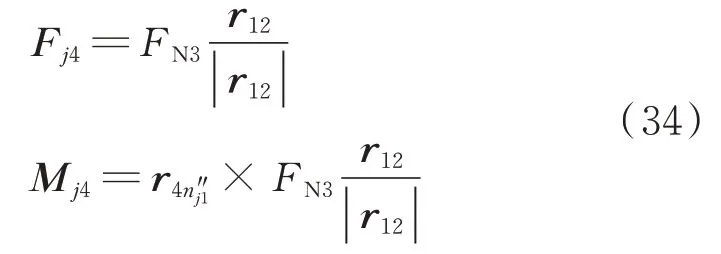
将销轴挡板在接触点受到的碰撞力平移到点1，需要同时施加如6 图所示的力Fi1和力矩Mi1：

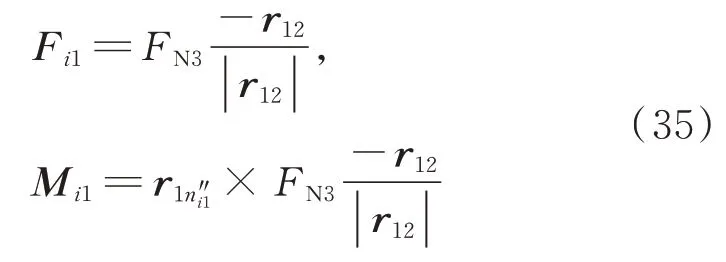
接触点处的摩擦力等效和接触力类似。

3.2 面碰撞的等效施加

当销轴挡板和轴套发生面碰撞时，采用相同的等效方法，在平面▱124 上，将轴套45 所受的碰撞力FN平移到点4，得

销轴所受的碰撞力FN平移到点1，得

3.3 含间隙铰链碰撞合力模型

当含间隙铰链存在N个接触碰撞点，等效施加后，各节点上附加的非线性铰链力由上述各种碰撞类型的碰撞力集成得到，如“T”字型等效梁模型中节点1、4、2、5 上作用总的接触碰撞力为

然后将非线性铰链力等效施加到图2中“T”字型模型的节点1、2 和4、5 上，得

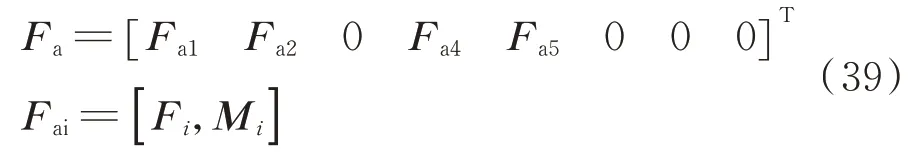
式中：Fi、Mi见式（38）。

4 含间隙铰链数值仿真

4.1 含间隙铰链模型验证

为了研究间隙的存在对含间隙铰链结构动力学特性和响应的影响，设计如图7 所示的含间隙铰链“T”字型模型作为研究对象，黑色线条表示销轴，红色线条表示轴套。含间隙铰链模型的轴向为z向，长度为1.0 m，在中点处有一个含间隙铰链。模型的顶点No.7 节点6 自由度固定约束，下部节点No.8 施加外部激励。销轴的两端节点编号分别为No.1 和No.2，中点编号为No.3，销轴中点和顶点No.1 连接。轴套的两端节点编号分别为No.4 和No.5，中点编号为No.6，轴套中点和下部节点No.8相连。销轴的长度为0.04 m，轴套的长度为0.038 m。初始时刻，销轴和轴套轴线重合。

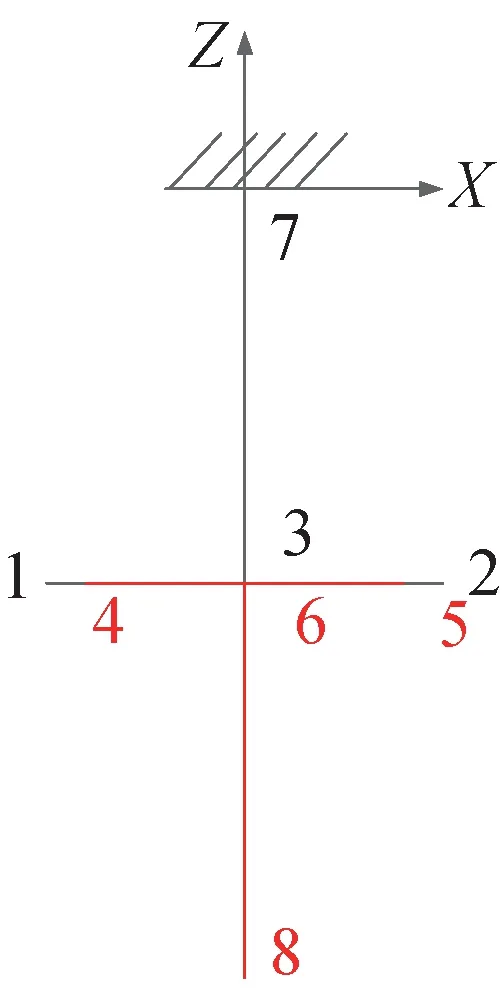
图7 含间隙铰链分析模型Fig.7 Analysis model with clearance joints

销轴半径为0.047 m，轴套内半径为0.05 m，轴套外半径为0.055 m。梁37 和68 的材质为复合材料（弹性模量E=45 GPa，泊松比为0.34）。销轴和轴套的材质为不锈钢（弹性模量E=206 GPa，泊松比为0.3）。

在下部节点No.8 施加轴向的脉冲激励

总分析时长为5.0 s，作瞬态动力学响应分析，各个节点的位移响应时程如图8 所示，其中脉冲激励作用过程0 ≤t≤0.01 s 时间段各个节点的位移响应时程被放大显示。

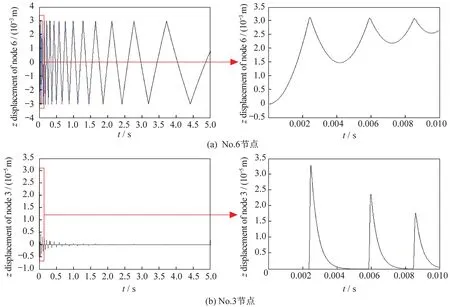
图8 各节点UZ 位移响应Fig.8 UZ displacement response of each node

与ANSYS 软件仿真结果进行对比，含间隙铰链模型仿真得到的自由端No.8 节点对应于ANSYS 软件分析模型中的No.5节点，两者仿真结果中UZ位移响应如图9所示，可以看出响应曲线形状非常相近。

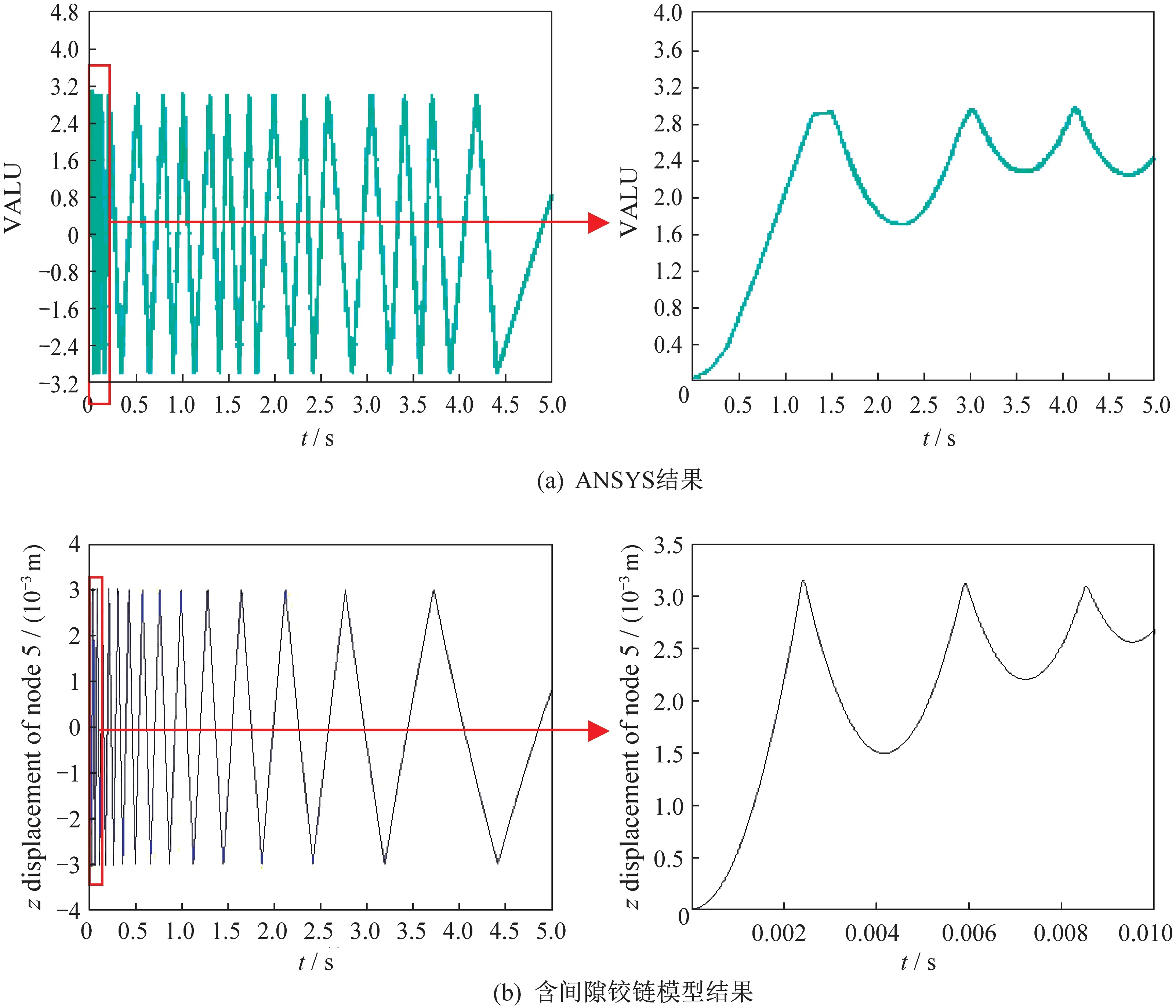
图9 No.8 节点UZ 位移响应Fig.9 UZ displacement responses of No.8 node

节点No.3 和No.6 的初始z向间距为1 mm，径向间隙大小为3 mm。铰链模型中节点No.3 和No.6 之间的UZ位移差响应时程如图10 所示，可见位移差在−2～4 mm 之内，从而验证了前述含间隙铰链模型采用施加附加非线性力来处理间隙的方法的正确性。

图10 节点No.3 和No.6 的UZ 位移差响应时程Fig.10 UZ displacement difference response of No.3 and No.6 nodes

在轴向振动过程中，1 节点附近发生径向碰撞，各个时刻碰撞点的z坐标随时间变化情况如图11 所示。可见大部分时间没有发生径向碰撞，发生碰撞时径向碰撞点的z坐标为−0.547 和−0.453 m。其中，脉冲激励作用过程0 ≤t≤0.01 s 时间段碰撞点的z坐标随时间变化情况如图11（b）所示，发生碰撞时径向碰撞点的z坐标为−0.547 m。考虑到销轴轴线的初始z坐标为0.5 m，轴套的内半径为0.047 m，从而验证了前述推导的接触碰撞分析和潜在碰撞点公式的正确性。

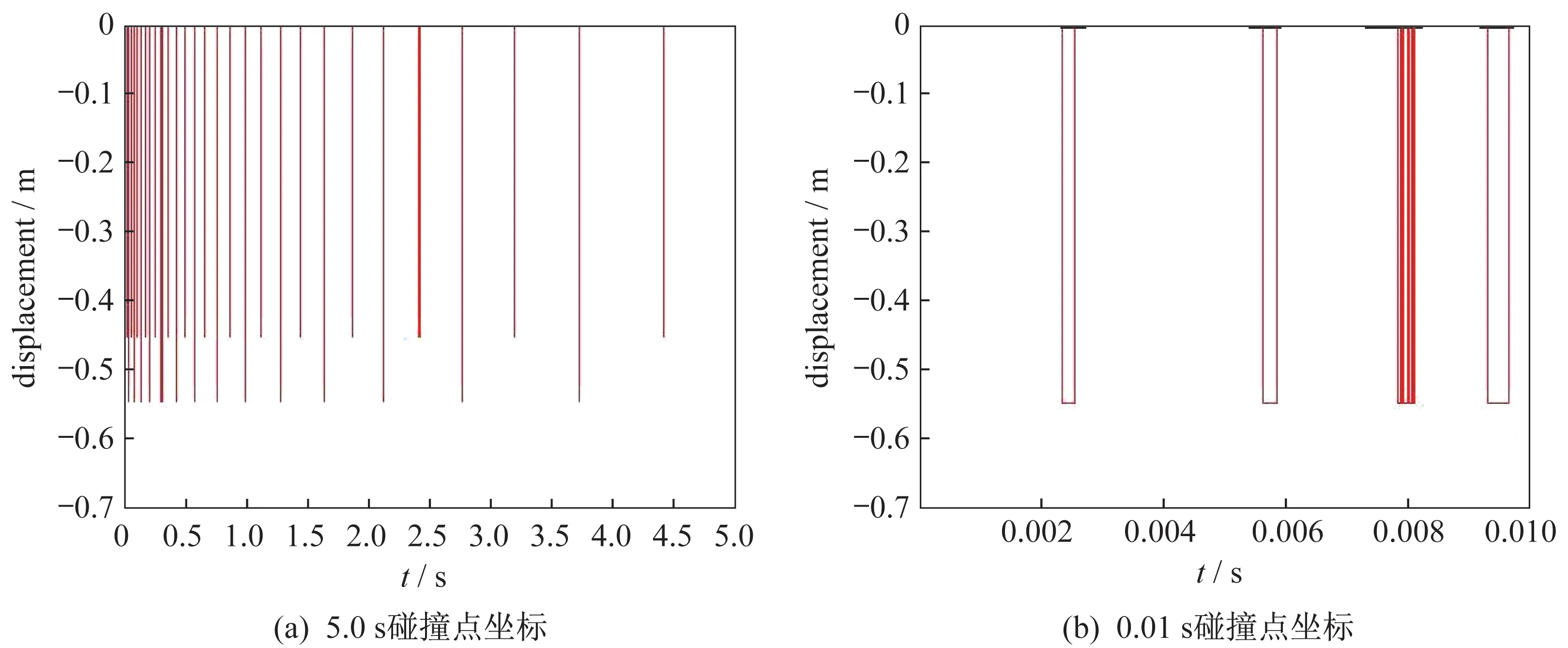
图11 径向碰撞点Z 坐标变化情况Fig.11 Changes of the Z coordinates of the radial collision points

图12 基本桁架单元Fig.12 Basic truss unit

计算效率方面，由于本算例模型比较简单，自编程序和ANSYS 软件的计算时间相当。对于复杂结构模型，自编程序的计算时间更长，后续需要改进自编程序的动力学时程积分算法及程序实现。

4.2 有间隙桁架天线的非线性动力学仿真

超大尺寸桁架天线一共有18 个如图12 所示的基本桁架单元，建立含间隙铰链的超大尺寸桁架天线的一个单元模型，如图13 所示。模型中一个隔板下有两根连梁，该连梁中有两个含间隙铰链，另一个隔板下也有两根连梁，该连梁中有一个含间隙铰链。模型左端隔板3 个顶点固定约束。

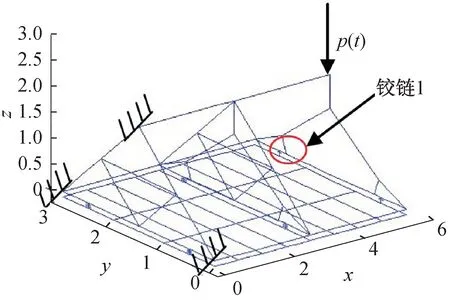
图13 含间隙铰链的桁架天线模型Fig.13 Truss antenna model with clearance joints

在桁架天线的自由端截面顶点施加脉冲激励

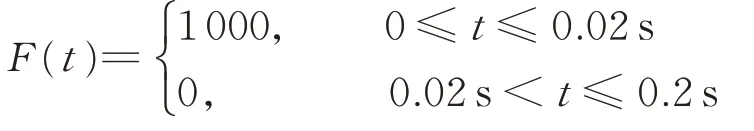
作瞬态动力学响应分析，得到各个节点的动力学响应时程，包括位移、速度、加速度等。模型自由端截面连梁中，含间隙铰链1 销轴中点No.98 的位移时程曲线如图14 所示。销轴中点No.98 和轴套中点No.101 之间的位移差时程曲线如图15 所示。

桁架天线的自由端截面顶点No.37 的振动位移时程曲线如图16 所示。各关键节点的振动速度和加速度时程曲线同样也可以得到。

图14 点No.98 的位移时程曲线Fig.14 Displacement curves of No.98 node

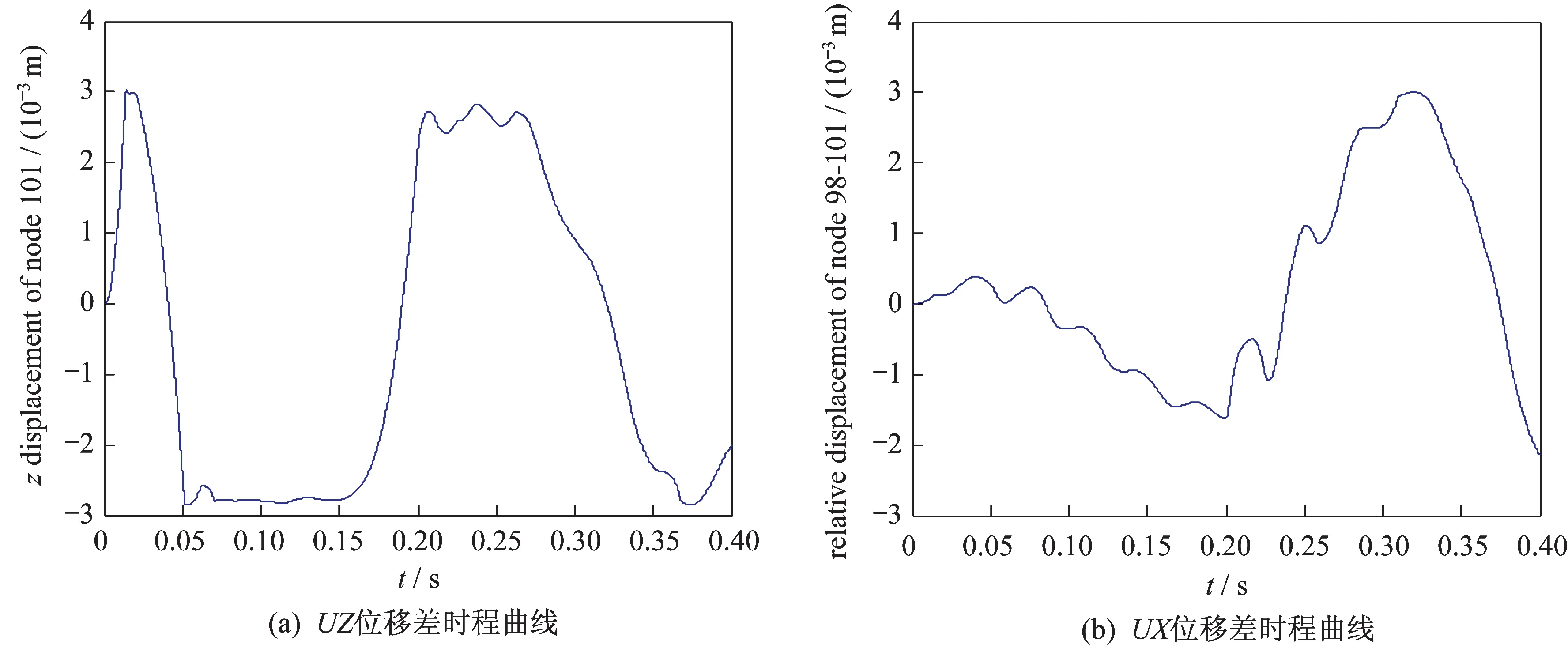
图15 位移差时程曲线Fig.15 Displacement difference curves

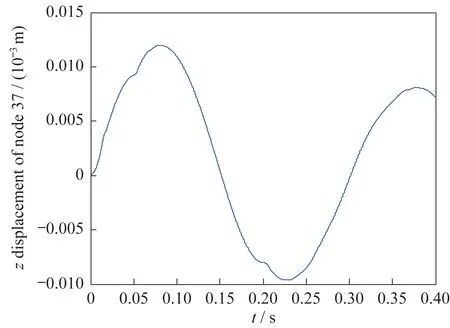
图16 点No.37 的位移时程曲线Fig.16 Displacement curve of No.37 node

由分析结果可知：在外部载荷作用下，桁架开始振动。由于间隙的存在，面阵保持静止。0.013 9 s 左右时，含间隙铰链1中销轴和轴套的径向位移差超过了预设的间隙大小，含间隙铰链销轴和轴套发生碰撞，铰链中产生非线性附加力，使得面阵开始振动。经过一段时间后，上、下部节点的位移差又小于间隙，含间隙铰链处于分离状态，此时非线性附加力为零，桁架和面阵分别独立振动。随着时间推移，含间隙铰链不断在接触和分离两个状态中变换。在此过程中，含间隙铰链销轴和轴套中点的位移差一直在间隙大小±3 mm 之内。

5 结束语

本文建立了含间隙铰链的非线性动力学模型，将含间隙铰链等效为“T”字型模型，研究了铰链中各部件的碰撞检测算法，发展了不同状态的接触力分析模型及非线性铰链力施加方法。分析了“T”字型等效梁模型在轴向冲击载荷下的动力学响应，得到位移、速度、加速度时程曲线，并可得到碰撞状态和碰撞点、碰撞力等信息。与ANSYS 软件中组合单元模型的分析结果进行比较，验证了本文提出的含间隙铰链非线性动力学模型的有效性。基于该模型，分析了含多个含间隙铰链的可展开桁架结构在冲击载荷下的动力学响应，结果表明：采用含间隙铰链的动力学模型可以得到位移、速度、加速度等动力学行为。

后续将针对不同的含间隙铰链，发展更合理的非线性接触力分析模型，并将本文提出的含间隙铰链非线性动力学模型应用于机构多体动力学分析中。含间隙铰链的试验研究困难较大，将发展含间隙铰链的试验测试技术，测试出不同类型载荷下铰链中的瞬态碰撞状态和碰撞力、摩擦力等，并和本文仿真结果进行对比。