一种新的适用于拉曼成像的插值方法

席 杨， 李月娥

兰州大学信息科学与工程学院， 甘肃 兰州 730000

引 言

随着人类对生命科学的不断探索， 从亚显微水平对细胞的内部结构、 功能、 物质间传输进行活性定位与实时监测， 对于生命结构的理解以及疾病的诊治都有着十分重要的意义。 而拉曼光谱能够揭示分子的振动信息， 同时兼具无损、 非接触、 指纹性的优点， 使得拉曼检测技术被广泛应用于生物学， 化学和材料科学等诸多学科中[1-3]。

拉曼成像是一种特殊的成像技术， 它通过采集样本某点处的拉曼信号， 选择指定谱峰的强度、 谱峰面积或者谱峰宽等参数并以灰度图或伪色图的形式显示， 图像明暗、 色彩的变化与指定谱峰所代表的物质成分相对应， 便可提供物质的浓度、 分布状况等生物信息。

从人力、 财力、 耗时的角度来看， 拉曼检测的采集点不宜过多， 从采集信息的完整度来看， 采集点又不宜太少， 通常实验得到的拉曼成像含有有限的像素点， 为了满足人们的视觉要求， 一般要对它进行插值放大(即分辨率增强)。 目前关于图像插值方法的研究， 包括广泛使用的最近邻域法、 双线性内插法、 三次样条内插法[4-5]， 以及基于小波变换的图像插值方法[6-8]。 使用这些方法对常规的图像进行处理的实质是根据已知像素点， 选择合适的插值函数进行插值， 其结果是像素点有所增加， 视觉效果得到改善， 但对于拉曼检测， 还需考虑采集点处采集信息的真实分布情况。 此外， 如图1所示， 两个采集点处都是以高斯光束进行激发，d表示两个采集点之间的距离， 如果要在两个采集点之间进行插值， 则需考虑相邻高斯光束之间存在交叠的现象， 理论上， 该处插值受附近采集点处高斯光束的共同影响。 本文将基于这些特性提出一种更合理的适用于拉曼成像的插值方法。

图1 两个相邻采集点处的高斯光束存在交叠

1 实验部分

1.1 信息采集

我们以共振拉曼探针标记的细胞成像为例[9]， 对新插值方法进行检测。 拉曼信号的采集使用了Witec共焦拉曼系统， 激发波长为532 nm， 激光功率为5 mW， 每点处拉曼信号的积分时间为1 s。 采集区域的面积为22 μm×22 μm, 一共采集了32×32个点， 可知相邻像素点之间的距离为22/31 μm, 物镜采用Plan Apo 60 NA=1.4 (Nikon, Japan)的油镜， 高斯光束的束腰直径约为1 μm。

1.2 光谱预处理

由于受实验仪器、 环境以及荧光的影响， 采集的拉曼信号通常含有较大的噪声与背景漂移[10-11]。 事实上， 光谱采集的过程中， 来自环境中的宇宙射线、 α射线和γ射线也会照射到探测器上并形成一系列非常尖锐的谱峰， 其宽度通常不超过2 cm-1， 称为尖峰。 本文中， 我们使用已有的处理方式完成去尖峰[12]、 去噪[13]和基线校正[14]。 我们从32×32个采集点中选择采集点(15, 7)处的拉曼信号进行呈现， 如图2所示， 这里指定谱峰的波数范围为1 027～1 480 cm-1。 此外， 由于受实验仪器的影响， 光谱左端区域1内存在较大漂移， 因此我们统一对1 024个采集点的光谱左端进行了截断处理。

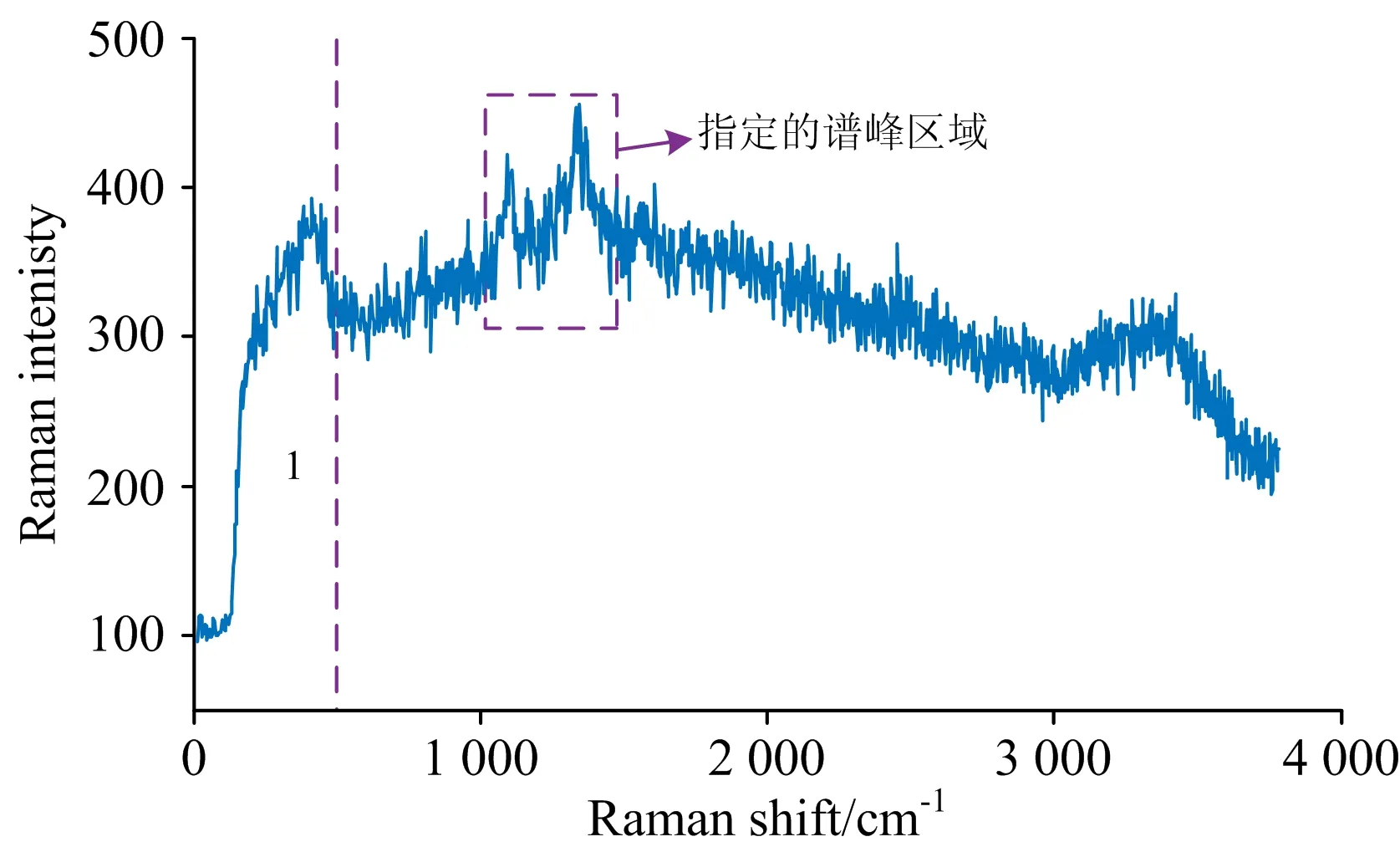
图2 采集点(15, 7)处的拉曼信号

1.3 原始成像

对每个采集点处的拉曼信号进行预处理， 选择指定谱峰的面积作为返回参数， 并进行归一化显示， 得到对应该采集区域的灰度图及伪色图(绿色)， 如图3所示， 图像中的明暗分别对应了细胞中被标记线粒体浓度的高低。

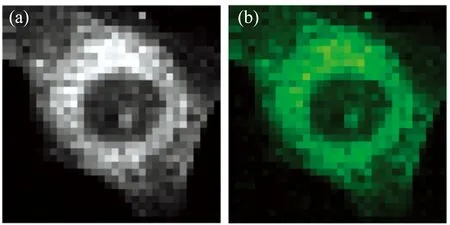
图3 共振拉曼探针标记的线粒体拉曼成像

2 基本原理

我们选择将原始成像放大两倍(即64×64个像素点)来说明插值的思想。 通过取两个相邻高斯光束的中心垂直截面得到如图4中对应的f(x)截面函数，d表示两个采集点a和c之间的距离,b为a与c的中心插值点， 高斯光束的截面函数f(x)由式(1)给出， 其中，x表示插值点到采集点之间的距离。

(1)

需要注意的是， 实验中采集的拉曼信号与高斯光束的能量成正比， 高斯光束能量的截面函数由式(2)给出， 对应图4中的函数f2(x)。

(2)

此外， 拉曼信号的采集不是指单点处的采集， 而是以采集点为中心指定区域内的采集， 指定区域由高斯光束能量函数的束腰决定。 如图5所示为图1中两个高斯光束能量的俯视图， 两个采集点处的采集区域分别为图5中两个虚线圆所对应的部分， 虚线圆的直径即为对应的高斯光束能量的束腰直径， 这里模拟的是相邻采集点处采集区域(即虚线圆部分)相切的情形， 而这也是本文实现插值的关键， 后面将详细介绍。

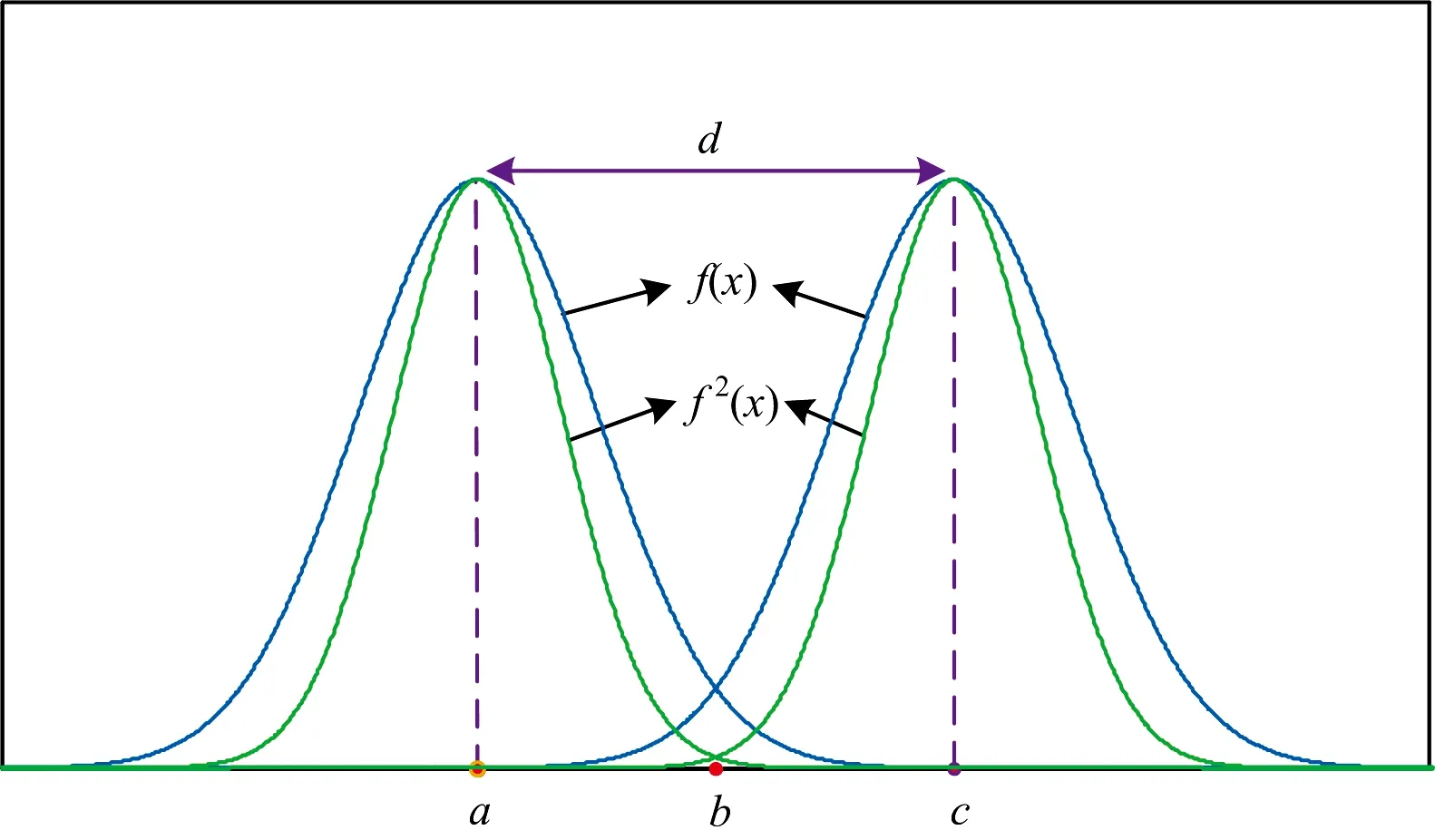
图4 采集点a和c处高斯光束的截面函数f(x)及其能量的截面函数f2(x)

Fig.4 The cross-sectional functionf(x) of the Gaussian beam at pointsa，cand the cross-sectional function of its energyf2(x)

图5 相邻采集点处高斯光束能量的俯视图

我们知道， 高斯光束的束腰是由峰强下降到最大峰强的e-1所决定的， 将其代入式(1)可得

(3)

已知本文中使用的束腰为1 μm, 所以x=0.5 μm， 可以得到

w=x=0.5

(4)

将w代入式(2)得

(5)

从而得到各个采集点处高斯光束的能量函数

(6)

其中，Bi表示第i个采集点处高斯光束能量函数的幅值，x与y分别对应高斯光束在水平面沿x轴与y轴到中心处的距离， 每个采集点处面积参数是已知的， 通过对式(6)选择以束腰直径的指定区域并对其积分可反推出每个采集点对应的系数Bi， 进而得到每个采集点处真实的高斯光束的能量函数， 由于各个像素点处的值不一致， 与其对应的能量函数的幅值也不尽相同， 但是束腰仍然是统一的。

拉曼信号采集过程中， 在选定高斯光束束腰的前提下， 调整采集间隔， 使相邻采集点的间距和高斯光束能量函数的束腰直径满足d=2k。 如图6所示为相邻采集点a和c处高斯光束能量的截面图， 当满足d=2k时[图6(a)]， 中心插值点b处估计值由a2和c1两部分构成， 此时b处估计值刚好为a和c处值之和的一半， 这种处理方式符合插值要求， 且不会产生比所依赖像素点的最大值大的插值。 当d>2k时[图6(b)]， 中心插值点b处预测值由b1和b2两部分构成， 此时b处估计值明显小于a和c处值之和的一半， 这是因为采集间隔较大， 采集点之间存在一小段未采集区域导致的， 基于此得到的插值普遍较小， 成像效果随d>2k程度的变大而变差。 当d<2k时， 采集间隔较小， 理论上中心插值点b处估计值会产生比所依赖像素点的最大值大的插值， 这是不符合插值要求的， 同时消耗的实验资源也比较多。

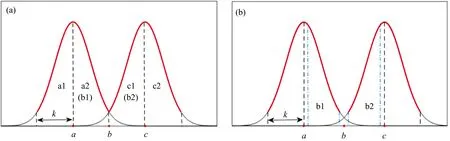
图6 相邻采集点a和c处高斯光束能量的截面图

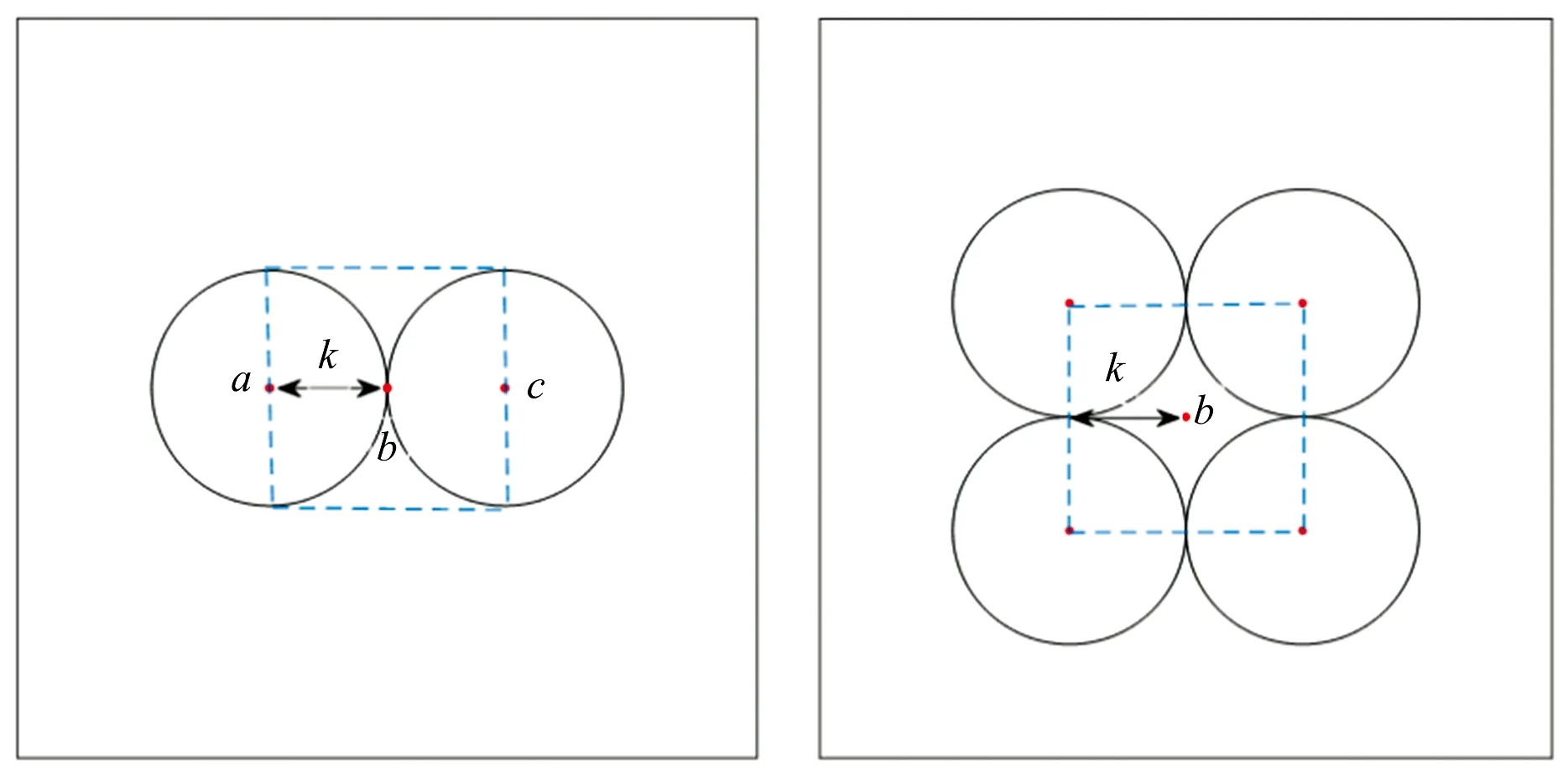
图7 插值点b处插值的形成

3 结果与讨论

为了便于理解， 我们以四个原始像素点(对应采集点处的面积参数)为例， 对其放大两倍的具体步骤如图8所示， 插值过程如下：

(1)选定四个原始像素点， 相邻像素点之间的距离为d。

(2)进行边界延拓， 本文中的处理方法是让边界点的值与前一个原始像素点的值保持一致。

(3)以小框中的像素点为例， 水平或垂直相邻的像素点之间的插值点由前后或上下像素点处的值决定， 而四个像素点中心的插值点由周围四个像素点共同决定。

(4)将步骤(3)中的小框看作一个运行窗， 遍历所有像素点得到(4)中的处理结果， 可以看到(4)中大框右侧与底部的边界点没有实现插值， 对其忽略， 这样(4)中大框即为二倍插值的结果。

图8 以放大两倍为例的插值步骤

基于上述插值原理对原始成像进行插值， 得到放大后的图像(64×64个像素点)如图9所示， 通过对比放大前后的成像可以看到， 原始图像由于像素点较少， 视觉上存在严重的马赛克现象， 而放大后的图像由于像素点增加， 成像效果更为舒适， 现实中我们可以根据实际要求将该方法推广至更高的放大倍数。

图9 基于新的插值方法放大两倍的效果

4 结 论

介绍了拉曼成像的基本原理， 并重点阐述了一种适用于拉曼成像放大的新方法， 该方法基于采集点处信息与高斯光束能量之间的联系， 在符合插值要求的情况下对拉曼成像实现插值放大， 同时对成像进行插值放大亦可大大降低采集相同像素点数目所耗的时间。 将新方法应用到实验采集到的拉曼成像中， 得到了良好的放大效果， 同时我们相信该方法可以作为拉曼成像放大处理的有力工具。 此外， 该新方法还具有在其他光谱成像放大中应用的潜在价值。