雾状钠火钠滴燃烧比率的模拟及应用

王国芝，张东辉，李世锐，申凤阳，杜海鸥，王荣东，胡文军

(中国原子能科学研究院，北京 102413)

钠冷快堆是第4代核能系统中的重要堆型，世界上很多国家都发展过或正在发展钠冷快堆。我国已建成第1座钠冷快堆——中国实验快堆(CEFR)，目前我国正在建设600 MW示范快堆(CFR600)。钠冷快堆使用液态金属钠作为冷却剂，冷却剂钠的用量为数吨到数千吨。化学性质活泼的液态金属钠暴露到空气中易引起燃烧，大量的钠是快堆厂房存在的最大火灾危险源。因此钠火安全问题是钠冷快堆区别于水堆的最重要的安全问题之一。与钠火相关的风险主要是钠燃烧后释放的热量使钠工艺间温度升高、压力增加以及释放出钠气溶胶。钠泄漏后可能发生池式钠火和雾状钠火，其中以雾状钠火的后果最为严重，因雾状钠火条件下钠喷射分散成小液滴，使钠燃烧特别剧烈。因此，需针对钠火安全问题，特别是雾状钠火安全问题，采取钠火防护措施，进行钠火安全防护设计和钠火事故分析。因此，需建立钠火的模拟计算方法，特别是对雾状钠火进行模拟计算，分析其后果。

世界上发展过钠冷快堆的国家，曾建立了多种雾状钠火的模拟计算方法，并开发了相应的雾状钠火分析程序。其中1类是采用集总参数的钠火分析程序，如SPRAY/SPRAY-3A[1]、SOMIX/SOMIX-2C[2]、NACOM[3]、SPCA-Ⅱ[4]、SOFIA[5-6]/SOFIA-2、CONTAIN-LMR[7]、MELCOR[8-10]、ASSCOPS[11-12]、SPHINCS[13-14]、HISLAC[15]、FEUMIX[16]、PULSAR[17]、NABRAND[18]、NAFCON-SF[19]、ECART[20]、SSPRAY[21]、SPCOM[22]等。另外1类是三维的钠火分析程序，如日本开发的雾状钠火计算程序SOLFAS[23-24]、AQUA-SF[25-26]，与NACOM等集总参数程序不同的是，SOLFAS和AQUA-SF中考虑了温度和压力的空间分布。张斌等[27]基于液滴燃烧的D2规律开发雾状钠火程序用于计算雾状钠火导致的气体温度和化学成分的空间三维分布。

综上，雾状钠火的模拟方法可分为两类。1类是采用集总参数法的雾状钠火程序，利用液滴燃烧的D2规律等经验公式，不考虑温度和压力的空间分布。优点是计算速度快、可用于计算雾状钠火对多个钠工艺间的影响。缺点是不能计算三维空间内的温度场和压力场等，而且由于钠滴粒径分布等数据很难精确测量，所以程序的验证存在困难。另外1类是利用现代计算流体力学的方法，通过求解三维空间的Navier-Stokes方程，优点是能计算温度和压力的三维分布，而且可较精细地模拟雾状钠火中的一些特殊现象，如钠火燃烧区局部缺氧对燃烧造成的影响。缺点是模拟越精细，消耗的计算资源越多，计算速度越慢，局部的精细计算和大空间、多工艺间的整体计算较难同时满足。

本文通过对雾状钠火燃烧的速率进行拟合，将雾状钠火作为钠工艺间内的热源和钠气溶胶源，模拟分析雾状钠火的燃烧过程。雾状钠火的燃烧速率与钠火的剧烈程度、钠火的后果直接相关。在这种模拟方法中，将钠滴的燃烧比率曲线或雾状钠火的燃烧速率曲线作为输入，忽略这中间具体的燃烧过程和现象，通过推导得到雾状钠火燃烧和单个钠滴燃烧的关系，重点关注雾状钠火燃烧速率对事故工艺间的温度、压力和钠气溶胶浓度变化的影响。在实际应用本文模拟方法时，可使用钠滴试验测量得到的钠滴燃烧比率曲线或钠火试验测量得到的钠燃烧速率曲线作为输入，将模拟结果与试验结果进行对比。但由于实际试验测量的钠滴燃烧比率曲线或钠燃烧速率曲线仅是在特定的试验条件下产生的曲线，不具有普遍性，当钠喷射质量流量或工艺间体积等试验条件发生变化时，便不再适用。因此本文分别采用幂函数、指数函数和线性函数模拟钠滴燃烧比率曲线，用钠滴最大燃烧比率、钠滴下落时间等参数表征钠滴的燃烧比率曲线。

1 钠滴燃烧比率模拟

1.1 钠滴燃烧比率

将钠滴的燃烧分为预燃阶段和燃烧阶段，钠滴的燃烧由氧气向液滴表面的扩散速率控制。预燃阶段的反应速率为：

(1)

其中：mf为钠滴质量，kg；ρO2为氧气质量浓度，kg/m3；Dd为传质系数，m3/s；D为钠滴粒径，m；i为钠燃烧反应生成过氧化钠的钠质量和钠燃烧总质量的比值；Re为Reynolds数；Sc为Schmidt数；t为时间，s。

燃烧阶段的燃烧速率利用准静态液滴的燃烧模型计算，并通过强制对流修正：

(2)

其中：cpg为空气的比定压热容，J/(kg·K)；Pr为Prandtl数；B为系数；k为气体的热导率，W/(m2·K)。

基于上述经验关系式，编制雾状钠火的计算程序，并进行了验证[28]。在初始环境氧气浓度为21%、钠滴平均粒径为4.576 mm下，假设其下落4 s后进入钠池，通过雾状钠火计算软件可计算得到钠滴燃烧比率和下落时间的数据(表1)。钠滴落入钠池后，不再以雾状钠火形式燃烧，因此钠滴燃烧比率不再变化，达到该条件下的最大值80.28%。

表1 钠滴燃烧比率和下落时间的关系Table 1 Sodium droplet combustion ratio vs. falling time

从表1可知，钠滴在下落过程中，钠滴燃烧比率逐渐增加，在第4 s时钠滴进入钠池，因此钠滴燃烧比率在第4 s时达到最大值80.28%。进入钠池后，认为钠滴汇聚成池以池式钠火形式燃烧，不再以雾状钠火形式燃烧，因此当下落时间大于4 s时，钠滴的燃烧比率均为最大值80.28%。除了利用雾状钠火程序计算，也可设计试验装置，在一定初始条件下，测量得到特定粒径的钠滴在空气中的下落燃烧比率和时间的关系曲线。

为模拟计算的方便，需对钠滴燃烧比率和时间的关系进行函数拟合，拟合成如下的分段函数关系式：

(3)

其中：Rd(t)为钠滴燃烧比率和时间的函数；τd为钠滴在空中下落的时间；Rm为钠滴下落到钠池的燃烧比率，对于表1，τd=4 s，Rm=80.28%。表1是特定工况下的数据，当初始条件变化，或工艺间高度变化，或钠滴粒径变化时，对应的数据不同，因此相应的τd和Rm也不同。

1.2 幂函数模拟钠滴燃烧比率

雾状钠火物理模型中，通常认为液滴燃烧满足D2规律。D2规律认为钠滴在燃烧的过程中，粒径的平方和下落时间呈正比，即：

(4)

其中：Dt和D0分别为t时刻和初始时刻的钠滴粒径，m；k1为比例系数。而钠滴燃烧比率和钠滴粒径的3次方呈正比：

(5)

联立式(4)和(5)可得：

(6)

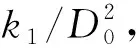
R(t)=(1-k2t)1.5

(7)

式(7)中燃烧比率为时间的幂函数，因此称之为钠滴燃烧比率的幂函数模拟。表1所列的钠滴燃烧比率，用式(7)模拟，可计算得到k2=0.165 4。利用幂函数模拟的燃烧比率曲线和程序计算得到的燃烧比率曲线如图1所示。

图1中虚线表示使用程序计算得到的在1.1节的试验工况下钠滴燃烧比率曲线。在不同的工况下，钠滴的最大燃烧比率和下落时间与表1的不同，但燃烧比率曲线变化趋势与图1的相似。从图1可知，在钠滴下落时间较小时，式(7)拟合得到的钠滴燃烧比率较程序计算的更大，这可能是因为使用幂函数模拟时，认为k1是常数，使用初始条件计算得到。实际上k1与环境条件和钠滴温度等相关，因此程序计算得到的钠滴燃烧比率和幂函数模拟得到的钠滴燃烧比率会有差异。

图1 程序计算和幂函数模拟的钠滴燃烧比率Fig.1 Sodium droplet combustion ratios calculated by code and fitted by power correlation

1.3 指数函数模拟钠滴燃烧比率

依据燃烧比率曲线的特点，参考FEUMIX软件中对钠火燃烧功率参数Sh(Sh为钠滴和空气的换热面积和传热系数的乘积，W/K)[29]的模拟，用如下的指数函数来拟合燃烧比率曲线：

(8)

其中，A、θ为指数函数模拟钠滴燃烧比率关系式中的参数。A、θ、τd和Rm之间不是独立的，由于钠滴燃烧比率曲线应是无断点的，因此当t=τd时，有：

A(1-e-τd/θ)=Rm

(9)

可得出：

θ=-τd/lg(1-Rm/A)

(10)

对于表1的数据，τd=4 s，Rm=80.28%，因此仅需指定A，即可用式(8)拟合钠滴燃烧比率曲线。图2为当A分别取1和100时式(8)拟合和程序计算的钠燃烧比率曲线。

图2 程序计算和指数函数模拟的钠滴燃烧比率Fig.2 Sodium droplet combustion ratios calculated by code and fitted by exponential function

从图2可知，当A=1时，式(8)拟合得到的钠滴燃烧比率较程序计算的更大。当A=100时，式(8)拟合得到的钠滴燃烧比率与程序计算值吻合得更好。这是因为A越大，式(8)拟合得到的曲线越接近直线，而程序计算的钠滴燃烧比率也近似线性，因此两者能吻合得较好。但若用于安全分析需取保守值，则可选择较小的A。实际上，当A较大时或最大燃烧比率Rm远小于A时，有：

Rm≪A

(11)

因此钠滴燃烧比率函数如下：

(12)

当A较大时，模拟燃烧比率的指数关系式可用线性关系式替代，因此式(12)称为钠滴燃烧比率的线性函数模拟。

2 雾状钠火燃烧过程

2.1 钠泄漏流量不恒定

(13)

因此，t时已燃烧的钠质量msc为：

(14)

t′≤τd时，钠滴还未下落到钠池，空气中未燃烧的钠滴质量msj等于已泄漏的钠滴总质量msl减去已燃烧的钠滴质量msc：

msj(t)=msl(t)-msc(t)

(15)

将式(14)代入式(15)，可得：

(16)

τd

(17)

从τd时刻开始，钠滴已落到钠池，未燃烧的比率为1-Rm，则钠滴落入钠池的质量msp为：

(18)

因此，空气中未燃烧的钠滴质量等于泄漏的钠滴总质量减去已燃烧的钠质量和落入钠池的钠质量：

msj(t)=msl(t)-msc(t)-msp(t)

(19)

联合式(17)、(18)和(19)，可得空气中未燃烧的钠质量为：

(20)

在τe

(21)

由于钠泄漏已停止，钠泄漏质量达到最大值，类似地，可求出空气中未燃烧的钠质量之和为：

(22)

上述各式描述了在给定钠滴燃烧比率随下落时间关系的情况下，雾状钠火的燃烧过程，包括钠的泄漏、钠的燃烧和钠进入钠池，各部分钠的质量和钠滴燃烧比率以及钠泄漏流量的函数关系。

2.2 钠泄漏流量恒定

(23)

将式(23)代入已燃烧钠的质量等式(式(14)、(17)和(21))中，可得：

(24)

将式(23)代入空气中未燃烧钠的质量等式(式(16)、(20)和(22))中，化简后可得：

(25)

可看到，当钠泄漏流量恒定时，某时刻已燃烧的钠质量和钠泄漏流量呈正比，空气中未燃烧的钠质量和钠泄漏流量呈正比。

3 雾状钠火燃烧速率模拟

3.1 使用钠滴燃烧比率曲线计算

(26)

当钠泄漏质量流量恒定不变时，联合式(24)和(26)，可得：

(27)

使用幂函数、指数函数或线性关系式模拟钠滴燃烧比率，并代入式(27)，可分别求解出雾状钠火燃烧速率的表达式，以指数函数模拟钠滴燃烧比率的式(8)为例，求解得雾状钠火的燃烧速率如下：

(28)

由于雾状钠火的燃烧速率和钠泄漏质量流量呈正比，因此有：

(29)

式(29)表示钠泄漏流量为1 kg/s时对应的钠燃烧速率，对于表1的数据，τd=4 s，Rm=80.28%，当A取1时，假设τe=8 s，得到雾状钠火燃烧速率随时间的变化曲线如图3所示。

图3 钠泄漏流量为1 kg/s时雾状钠火燃烧速率和时间的关系Fig.3 Sodium spray fire combustion ratevs. time for sodium leak rate of 1 kg/s

从式(27)和图3可看出，t≤τd时，雾状钠火燃烧速率和钠泄漏的质量流量呈正比，与下落时间为t时的钠滴燃烧比率呈正比。τd

3.2 钠火试验测量

可通过两种试验获得雾状钠火的燃烧速率。一种是钠滴的下落燃烧试验，通过一定条件下单个钠滴的试验测量得到钠滴燃烧比率和时间的关系曲线，利用式(27)，便可计算雾状钠火的燃烧速率。另外一种是设计与事故时钠泄漏工况条件一致的雾状钠火试验，使钠管道流量、破口尺寸、液态钠温度和初始氧气浓度等与事故工况下的一致，便可测量和计算得到雾状钠火的燃烧速率。

4 雾状钠火模拟关系式的应用

雾状钠火的后果，包括事故时工艺间温度和压力的变化、空气中钠气溶胶浓度的变化等，与雾状钠火的燃烧速率直接相关。钠燃烧释放出的热量作为热源，这部分热量通过对流传热或辐射传热的方式，在空气、钠气溶胶、地面和墙面等之间分配。

图4 钠滴燃烧示意图Fig.4 Schematic of sodium droplet combustion

钠滴蒸发后形成钠蒸气燃烧，形成火焰层，在火焰层发生钠蒸气和氧气的反应，如图4所示。

假设在火焰层，钠的燃烧反应是非预混燃烧，即钠和氧气反应的速率远大于钠蒸气和氧气向火焰层的传质速率。依据化学反应方程式，氧气的消耗速率、钠的燃烧速率和氧化钠的生成速率呈正比。氧气的消耗速率便是氧气向火焰层的传质速率。假设反应全部生成氧化钠，生成氧化钠的反应发生在火焰层，则有：

(30)

在火焰层，氧气的消耗速率(即环境中氧气向火焰层的传质速率)、钠燃烧的速率(即钠滴中的钠蒸气向火焰层的传质速率)和氧化钠的生成速率之间符合化学反应方程式中的计量比，因此有：

(31)

(32)

钠滴火焰层和空气之间存在传质和传热。一方面，氧气从空气中进入火焰层；另一方面，火焰层中钠燃烧产生的热量传递给空气，传热主要由火焰层和空气的温差确定：

Qf→g=Sh(Tf-Tg)

(33)

其中：Qf→g为钠滴火焰层向空气的传热，W；Tf为钠滴火焰层的温度，K；Tg为空气的温度，K。

利用传热和传质的相似性，可从传热方程得出氧气的传质方程[29]如下：

(34)

其中，YO2为空气中氧气的质量分数。联立式(31)、(33)和(34)，可得：

(35)

因此，通过上式，可由某时刻的雾状钠火燃烧速率求解得到火焰层向空气的传热速率。

其他的传热关系式的求解可分为两类，其中1类是火焰层和其他介质之间的传热，如火焰层和墙壁的辐射传热、火焰层和钠池的辐射传热等，均与雾状钠火燃烧速率有关。火焰层和墙壁之间的传热为：

(36)

其中：Qf→w为钠滴火焰层和墙壁间的传热，W；Tw为墙壁的温度，K；Tref为辐射传热参考温度，K；Rf为系数，通常取值为0.2～0.5；εw为墙壁的辐射传热系数；τfw为钠燃烧火焰层和墙面间的透射率；Ff→w为钠滴火焰层向墙壁传热的角系数。

第2类传热是气体、墙壁和钠气溶胶间的传热，这类传热关系式不与雾状钠火燃烧速率直接相关，主要由温差、传热面积和传热系数确定，如气体和墙壁之间的传热：

Qg→w=hgwSw(Tg-Tw)

(37)

其中：Qg→w为气体和墙壁之间的传热，W；Sw为墙壁的面积，m2；hgw为气体和墙壁间的传热系数，W/(m2·K)。

综上，以雾状钠火燃烧速率为基础，可求出雾状钠火作用于钠工艺间的所有传质和传热，因此可求解得到雾状钠火的后果，包括温度和压力等。

5 结论

本文提出了钠滴燃烧比率模拟方法，以钠滴的燃烧比率和时间的曲线为基础，说明了雾状钠火的燃烧过程，得到了雾状钠火燃烧速率和钠滴燃烧比率之间的关系，并阐述了雾状钠火燃烧速率模拟的应用，主要的结论如下。

1) 雾状钠火燃烧过程中，钠滴的燃烧比率随时间逐渐增加，在钠滴进入钠池时达到最大值；钠滴的燃烧比率曲线可通过钠滴燃烧试验获得，可通过雾状钠火分析程序计算得到，可通过幂函数、指数函数和线性函数模拟和拟合钠滴燃烧比率曲线。

2) 利用钠滴燃烧比率曲线，可模拟计算雾状钠火的燃烧过程，求解出已燃烧钠的质量、空气中未燃烧钠的质量、进入钠池的钠质量和时间的关系曲线。当钠泄漏流量在雾状钠火燃烧过程中维持恒定时，已燃烧的钠质量和空气中未燃烧的钠质量与钠泄漏流量呈正比。

3) 雾状钠火的燃烧速率可通过钠滴燃烧试验和模拟事故工况下的雾状钠火试验得到。雾状钠火燃烧速率是一个逐渐增加，在准稳态维持燃烧直到钠泄漏停止，然后减少到0的过程。雾状钠火的燃烧速率与钠泄漏的质量流量呈正比，与空气中未燃烧的钠质量正相关。当空气中的钠全部进入钠池后，雾状钠火结束。

4) 使用雾状钠火燃烧速率模拟方法，以雾状钠火燃烧速率为基础，将其当成1个热释放源，可将和钠燃烧直接关联的现象，如钠的燃烧速率、钠进入钠池的速率、空气中未燃烧的钠的质量、钠燃烧产生钠气溶胶的速率、钠燃烧火焰层和空气间的传热、钠燃烧火焰层和墙壁间的传热等现象剥离进行计算。而雾状钠火燃烧过程中的其余传热和传质现象，与其他燃料的燃烧过程中的传热和传质现象相似，可用相似方法处理。

5) 钠滴燃烧比率曲线或雾状钠火的燃烧速率曲线可通过集总参数法的雾状钠火程序计算得到，也可利用现代计算流体力学的方法求解雾状钠火三维空间的Navier-Stokes方程得到，也可直接使用钠火试验测量得到。这种模拟方法忽略了钠滴燃烧的具体现象和过程，用钠滴的燃烧比率或雾状钠火燃烧速率代表雾状钠火的剧烈程度，重点关注钠燃烧速率对和安全有关的雾状钠火后果的影响，包括事故工艺间的温度变化、压力变化和钠气溶胶浓度的变化，输入方式灵活，且可与试验对比验证，可用于钠火事故安全分析中雾状钠火的模拟。