风、光高渗透率电网中考虑频率稳定的可再生能源承载力研究

郭小龙，毕天姝，刘方蕾，胥国毅，张 锋，王 衡

（1.国网新疆电力有限公司，新疆 乌鲁木齐 830002；2.华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

风电、光伏因其无污染、分布广、具备规模化利用价值等优势而受到重视[1]～[3]。汽轮机、水轮机等传统同步发电机组具有转子惯量和一次调频能力，当系统发生功率扰动时,能够通过旋转动能和调速系统来响应电网频率的变化。风电、光伏发电系统具有弱惯量或无惯量以及最大功率跟踪运行特点，无法及时响应系统的频率变化。可再生能源大比例地接入电网影响了电网的频率安全，因此，研究可再生能源承载力对于电网的稳定运行和可再生能源的高效利用具有重要意义。

限制可再生能源承载力的主要因素有电网调峰容量、电压稳定、频率稳定、线路传输能力[5]～[10]。目前，从频率稳定角度对可再生能源承载力进行研究的文献较少。大规模可再生能源电力接入，将压缩原有同步发电机发电容量，使得系统等效转动惯量降低。另外出于经济性的考虑，可再生能源发电系统一般运行在最大功率跟踪状态，不具备一次调频能力，增加了系统的调频压力，增加低频减载或高频切机的风险，如2015年9月，锦苏特高压直流发生双极闭锁，华东电网产生较大功率缺额，12 s 以后全网频率最低下降到49.56 Hz[11]。文献[12]指出，频率稳定已成为限制电网可再生能源承载力的主要因素。从频率稳定约束分析可再生能源承载力，须要考虑系统的频率响应特性。文献[13]论述了电网的频率响应特性，并在此基础上提出了SFR（系统频率响应）模型。文献[14]采用SFR 模型对比分析了可再生能源机组接入系统后与系统中仅有常规机组时的频率响应，但考虑的机组类型不够全面。文献[15]考虑了水轮机与再热式汽轮机两种机组，通过惯性环节来模拟发电机的调频响应，但这种方法在系统频率响应过程的初期精度较高，后期精度不够。文献[16]通过分析可再生能源接入后使系统惯量下降，增加系统对于备用容量的需求，提出可通过研究系统惯量来评估系统的可再生能源最大接入量的思路，但并未给出具体评估方法。文献[17]给出了系统中接入可再生能源后等值惯性常数的计算方法，可用于系统频率响应研究。

本文将考虑可再生能源及汽轮机、 水轮机等各类同步发电机组的频率响应特性，建立包含各类传统同步发电机组和可再生能源机组的频率响应综合模型，提出在频率稳定约束下电网可再生能源承载力的评估方法。

1 可再生能源电力系统频率特性

风电机组和光伏发电系统均通过换流装置和电网相连，不与电网直接耦合，其中风电机组虽然本身具有旋转动能，但是输出功率与电网频率变化解耦，无法为电网提供惯量响应，光伏发电单元无旋转动能，因而无法通过惯性响应释放动能。当风速改变时，对于风电机组控制，风电机组通过调节转子转速和叶片桨距角等措施使风机运行在最大功率跟踪（MPPT）状态[10]。光伏阵列的发电功率通过MPPT 控制，调节光伏阵列的输出电压，使光伏阵列获得最大的输出功率[18]。因此，可再生能源机组没有备用功率响应系统频率变化。

可再生能源无法为电网提供惯量支撑，同时在最大功率运行方式下，当系统中发生低频扰动时，不能够像传统机组那样通过调速系统作用，增加原动机的出力来增加机组的输出功率，从而稳定系统频率。因此，可再生能源接入系统会对系统频率特性造成影响[18]。本文将具体分析可再生能源电力系统的频率特性，并建立系统频率响应综合模型。

1.1 频率响应指标

电力系统的频率变化通常采用频率偏移量和频率变化率等指标来衡量。系统中典型频率下降曲线如图1 所示。系统频率下降可以用最大频率偏移量 Δfmax（最低频率 fmin）、频率变化率 dΔf/dt、稳态频率偏移量Δfn、 频率下降至最低值所需时间Tnadir等指标来评估。

图1 电力系统典型频率下降曲线Fig.1 Typical frequency dropcurve of power system

系统频率扰动主要由系统中的有功功率不平衡量引起[19]，即：

式中：M 为系统惯性时间常数；D 为负荷阻尼常数；ΔP 为功率不平衡量；P传统为传统同步发电机功率；P可再生能源为可再生能源发电输出功率；P负载为系统中的总负载。

惯性时间常数反映系统惯量，它与运行发电机转子转动惯量有关，其表达式为[19]

式中：TJ为发电机转子转动惯量；ωmB为发电机额定机械转速；WK为发电机转子动能；SB为机组基准容量。

多台发电机组的系统等值转动惯量为[19]

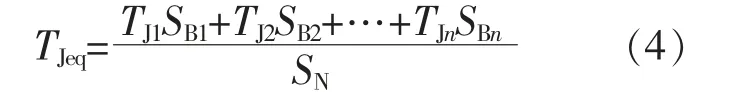
式中：TJeq为系统的等值转动惯量；TJ1，TJ2…TJn为系统中运行的单台机组的转动惯量；SB1，SB2…SBn为系统中运行的单台机组基准容量；SN为系统中发电机总容量。

最低频率fmin和频率变化率dΔf/dt 通常用作电网中保护元件以及控制装置的触发信号。在电力系统中，一般要求fmin不超过0.2 Hz[20]，即最低频率不低于49.8 Hz。我国未针对dΔf/dt 提出具体的标准，一些国家对该指标提出了低于0.4 Hz/s和 0.6 Hz/s 的标准[21]，[22]。本文取最大频率变化率限值为0.5 Hz/s[23]。

1.2 频率响应特性

目前，一般通过建立全网仿真模型，采用时域仿真获取频率响应，研究电网可再生能源承载力。当系统运行方式改变时，须要重新进行仿真计算，工作量较大且繁琐。由于系统频率响应特性主要与系统中各类机组容量、频率调节特性、系统等效转动惯量、负荷频率响应特性等因素有关，因此，本文通过建立包含这些因素在内的频率响应综合模型快速获得系统的频率响应，从而分析系统的可再生能源承载能力。

常见的同步发电机组主要包括非再热式汽轮机、再热式汽轮机和水轮机，本文主要考虑其调速器和原动机部分的特性[24]。

非再热式汽轮机主要考虑蒸汽惯性导致的蒸汽容积效应，采用一个一阶惯性环节延时来表示蒸汽容积效应，其表达式为

式中：ΔY 为汽轮机的气门开度变化量；ΔPm为输出机械功率的变化量；TCH为高压缸蒸汽容积时间常数。

再热式汽轮机传递函数为

式中：FHP为再热系数。

由于水流惯性引起的水锤效应，水轮机须要加入暂态斜率环节来获得稳定的控制效果。水锤效应传递函数和暂态斜率环节传递函数分别为

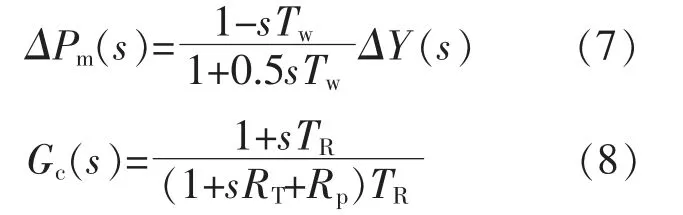
式中：ΔY 为导水叶开度变化量；ΔPm为输出机械功率的变化量；Tw为水锤时间常数；TR为水轮机复位时间；RT为水轮机暂时下降率；Rp为水轮机永久下降率。

在各类同步发电机原动机传递函数的基础上，结合调速器的传递函数并加入负荷阻尼作为影响因素，由此得到各类型同步发电机对应的传递函数框图如图2～4 所示。其中调速器模型为调速环节比例增益系数与一阶惯性环节，调速环节比例增益系数均用调差系数的倒数1/R，R 为发电机组的调差系数。

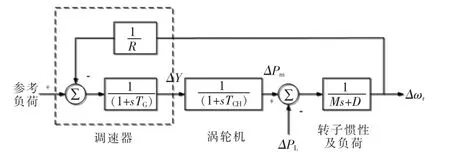
图2 非再热式汽轮机的发电机框图Fig.2 Block diagram of non-reheat steam turbine

图4 水轮机的发电机框图Fig.4 Block diagram of hydraulic turbine

由图2～4 可知，引入负荷阻尼影响的负荷-频率控制部分来体现负荷对于频率的调控，针对转子/负荷所影响的一阶惯性部分1/（Ms+D），发电机对于频率变化的响应主要表现在惯性常数M 上，负荷对于频率变化的响应则表现在阻尼常数 D 上，ΔPL为负荷变化量。

由式（1）可知，系统发生功率不平衡扰动时，在频率变化初始阶段，频率偏移量Δf 较小，系统中的频率变化率将主要与不平衡功率的大小ΔPL和系统的惯性时间常数M 有关；系统达到稳态频率偏移量时，dΔf/dt 为0，稳态频率偏移量将取决于功率不平衡量ΔPL和负荷阻尼系数D。下面以可再热式汽轮机组为例分析系统频率响应的影响因素，系统传递函数框图如图5 所示。

图5 系统频率响应传递函数框图Fig.5 Block diagram of frequency response transfer function

系统发生ΔPL的功率扰动后，有：

可得系统的频率响应为

考虑到扰动为阶跃扰动 PL（t）=Psu（t），Ps为扰动幅值，u（t）为阶跃函数，拉普拉斯变换后 Ps（s）=Ps/s，代入式（10）得到：

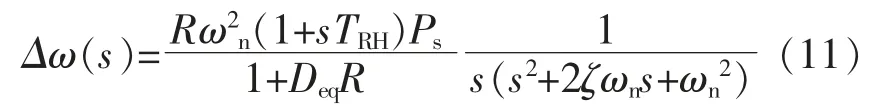
最终得到Δω 时域表达式为

由式（10）可得系统的稳态频率偏差为

系统频率变化率为dΔω/dt=sΔω，在频率扰动初始阶段最大，因此系统的最大频率变化率为

由式（12）可以看出，当系统中发电机的类型确定，其传递函数中的参数 TRH，FHP，R 等确定，系统的频率特性主要由等值惯性时间常数Meq、等值负荷阻尼常数 Deq和功率扰动量 ΔPL决定。式（13） 说明系统的稳态频率主要与 Deq，ΔPL有关。式 （14） 说明系统的最大频率变化率主要与Meq，ΔPL有关。系统中接入可再生能源机组后，由于可再生能源机组对电网表现出的弱惯量或无惯量特性以及最大功率跟踪运行方式，系统的等值惯性时间常数降低，出现功率扰动后功率不平衡量增大，系统的最大频率偏差和最大频率变化率增大。

1.3 频率响应综合模型

本文虑不同类型同步发电机组频率响应特性，增加可再生能源机组模型，建立频率响应综合模型，用于电网可再生能源承载力分析。将系统中各类同步发电机模型进行等值与聚合，得到电力系统常规机组模型参数，引入参考负荷来表示每类发电机组承担负载的比例。参考负荷代表不同类机组承担负载的比例，与各类发电机容量占系统总容量的比例有关。

为了反映整个系统以及负荷的频率特性，引入了系统的等值惯性时间常数Meq和等值阻尼常数Deq。Meq代表整个系统等效转动惯量，Deq代表着整个系统的等效负荷阻尼参数。Meq可由式（4）计算得到，由于可再生能源机组对电网表现出弱惯量或无惯量，简化考虑取其对系统的等效转动惯量为0；考虑到可再生能源接入前后系统的负荷频率特性无明显变化，Deq取值不变。

电网频率响应综合模型如图6 所示。

图6 电网频率响应综合模型框图Fig.6 Block diagram of power system frequency response comprehensive model

在Matlab/Simulink 中对四机两区系统[13]建立频率响应综合模型。四机系统如图7 所示，用一台等值可再生能源机组来替代原来的常规机组G4，分别用建立的综合模型和PSASP 软件对四机系统出现功率扰动后的频率变化情况进行仿真。设置系统中发生0.05，0.11 p.u.的功率扰动（负荷突增），两种仿真模型得到的频率变化曲线结果如图8 所示。

图7 四机两区系统Fig.7 Four-machine two-areas system

图8 四机系统频率响应曲线Fig.8 Four-machine system frequency response curve

由图8 可知，两种方法在不同负荷扰动情况下得到的频率响应曲线较为接近，系统的初始频率变化率、最低频率基本相同。在频率恢复阶段，两种方法存在一定的差异，引起差异是因为模型和仿真环境不完全不同，微小的结果差异不影响从频率变化率和最大频率偏差来评估可再生能源承载力。

目前，通过分析系统频率响应研究电网的可再生能源承载力，一般须建立全网仿真模型，采用时域仿真获取频率响应，如PSASP 软件。当系统运行方式改变时，须要调整运行方式进行仿真计算，其工作量较大且繁琐。通过建立综合模型，只须要确定系统中各类机组容量、频率调节特性、系统等效转动惯量、负荷频率响应特性，就可以快速获得系统的频率响应曲线，计算量小，结果准确快速。与分析软件建立全网仿真模型的模型相比，本文模型具有优越性。

2 系统可再生能源承载力评估

通过分析系统中各类机组的频率响应模型，建立了系统频率响应综合模型，运用综合模型可以快速得到系统在一定可再生能源渗透率下的频率响应曲线。改变系统中的可再生能源渗透率，得到相应运行方式下的频率曲线，通过最低频率和最大频率变化率这两个指标的限制，可以得到频率稳定限度下的电网最大可再生能源承载力。系统可再生能源承载力评估流程和具体算例如下。

2.1 分析流程

本文采用最大可再生能源渗透率来表示系统的可再生能源承载力，可再生能源渗透率的定义为

式中：ω 为可再生能源容量；S 为总容量

可再生能源承载力评估的具体流程如图9 所示。

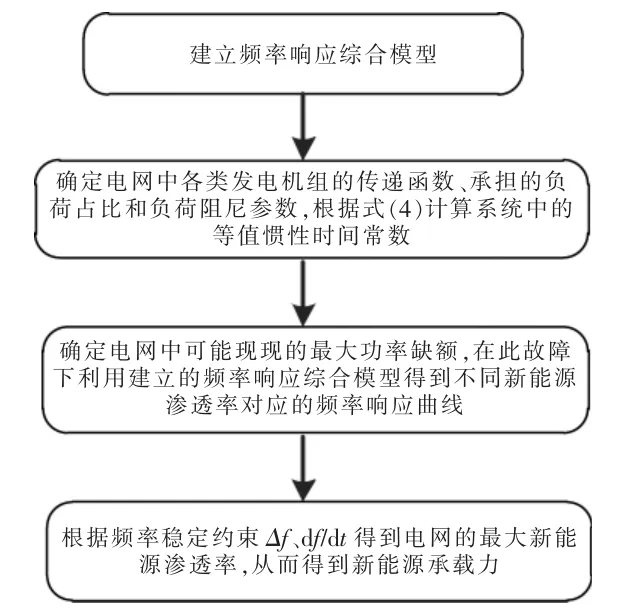
图9 可再生能源承载力评估流程图Fig.9 Flow chart for calculating maximum penetration level of renewable energy

2.2 算例分析

本文以某地区电网为例，对频率响应综合模型进行验证。该地区实际电网共有负载33 850 MW，系统中同步机组包含非再热式汽轮机、再热式汽轮机、水轮机。初始容量占比分别为41%，38%，5%，可再生能源类型为风电和光伏，可再生能源机组初始容量占比为16%，系统中各类发电机的等值参数如表1 所示。

该区域电网与区外电网存在功率交换，正常运行时与区外电网相连的最大联络线功率为2 000 MW。假定系统中该联络线发生故障，电网出现2 000 MW 的功率缺额，改变系统中可再生能源渗透率，得到不同可再生能源渗透率下的频率响应曲线如图10，11 所示。

表1 各类发电机等值参数Table 1 Equivalent parameters of various generators

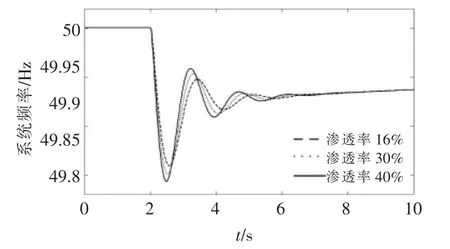
图10 不同可再生能源渗透率下频率响应曲线Fig.10 Frequency for different penetration of renewable energy

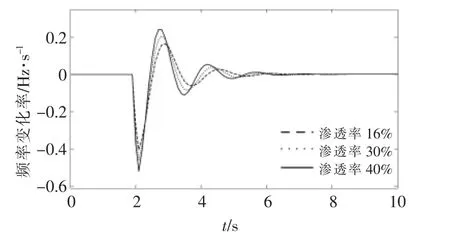
图11 不同可再生能源渗透率下频率变化率Fig.11 ROCOF for different penetration of renewable energy

由图10，11 可知，当系统中的可再生能源渗透率达到40%，系统发生2 000 MW 功率扰动时，最低频率达到49.84 Hz，最大频率变化率为-0.52 Hz/s，超过了0.5 Hz/s 的频率变化率限制。因此，该系统的最大可再生能源渗透率应低于40%。

当渗透率分别为35%，36%，37%时，得到系统的频率变化率最大处曲线如图12 所示。

图12 最大频率变化率Fig.12 Maximum rate of change of frequency

根据仿真结果，当电网中的可再生能源渗透率为36%时，最大频率变化率为-0.496 9 Hz/s，在频率稳定限度内，可再生能源渗透率为37%时，最大频率变化率为-0.501 1 Hz/s，超过了频率变化率的限定值0.5 Hz/s。

由以上仿真结果，可以得出该地区电网达到频率稳定极限的最大可再生能源渗透率为36%，即可最终确定该系统的可再生能源承载力。

3 结束语

本文考虑了传统同步发电机组和可再生能源机组的频率响应特性，建立了电力系统频率响应综合模型，利用综合模型快速获得系统发生功率扰动后的频率响应曲线。在此基础上根据描述系统频率变化的指标，频率变化率和最大频率偏移量来评估可再生能源承载力。本文验证了综合模型的可行性，并应用本文所提的方法对实例电网进行分析，在频率稳定约束下获得了电网的可再生能源承载力。