典型复杂地形影响下单台风力机布机方案数值计算研究

李 辉，李云涛，陈 飞，朱金峰，端和平，许 昌，3，李林敏

（1.中国能源建设集团 湖南省电力设计院有限公司，湖南 长沙 410007；2.河海大学 能源与电气学院，江苏 南京 211100；3.南京河大风电科技有限公司，江苏 南京 211300）

0 引言

我国低风速风电场多处于山区，其流场分布极为复杂[1]。研究复杂地形流场分布及其与风力机的耦合作用对山区风电场的微观选址、 发电功率预测等具有重要意义。

悬崖和高低山头地形在复杂地形中具有代表性，对此，学者们做了许多研究。魏祯[2]模拟了两山相邻的风场分布，结果表明，当山间距一定时，下游山坡顶和背风坡的风速平均偏差随上游山高度的增大而减小。杨祥生[3]对断崖等地形进行了数值模拟，研究了坡度对风速和湍流强度的影响，得出其随悬崖山坡高度增加而增大，随坡度增加而减小的结论。

针对风力机尾流效应，采用致动盘模型来简化风力机的方法受到了普遍关注。Sturge D[4]提出了一种将致动盘模型与全风轮相结合的CFD 方法，模拟尾流对下游风力机功率输出和叶片气动性能的影响。Nedjari H D[5]采用基于BEM 的致动盘模型模拟风力机，并根据不同的风电场布局评估大气边界层、 下风向尾流与地形之间的相互作用。褚景春[6]结合致动盘模型提出了一种单台风电机组尾流场数值模拟模型，结果表明，致动盘模型能够较好地捕捉尾流区的流场特性，尤其是较准确地反映机组远尾流区域的流场信息。

考虑到有无风力机时风力机前端入流速度存在较大差异，本文在模拟悬崖和高低山头地形流场特性的基础上，结合致动盘模型和拓展k-ε 湍流模型，进行了风力机不同布机位置下入流特性和输出功率的数值计算研究。

1 数值计算理论及方法

1.1 控制方程

本文采用RANS 和拓展k-ε 湍流模型相结合的方法，其中常物性不可压缩流体的控制方程为

式中：Su，Su，nac分别为致动盘推力源项、 机舱阻力源项，其只在致动盘识别区域内有效。

湍流模型采用EI Kasmi A[7]提出的拓展k-ε湍流模型。

1.2 致动盘模型

风力机致动盘模型是不对风力机进行实体建模，而是将风轮简化成一个空气可以自由通过，但具有一定阻力的圆柱形薄盘，风轮对空气来流的推力（T）以及机舱的阻力均以动量源项的形式加入到RANS 方程组中，风轮及其邻域通过网格几何位置进行辨识。由轮毂高度入流参考风速（UREF）可得到：

式中：Su为风轮推力源项；Su，nac为机舱阻力源项；V 为致动盘体积；CT为风力机推力系数；Δl 为致动盘厚度；CD，nac为阻力系数，通常取 0.8～1.0，本文模拟时取1.0。

不同于平坦地形，在复杂地形中，风力机轮毂高度处的入流风速在到达风轮前端时难以确定，本文采用文献[8]提出的改进致动盘推力源项的计算方法。

1.3 边界条件

本文采用中性大气边界层入口风廓模型[9]，其速度（u）和湍流动能（k）及其耗散率（ε）的入口轮廓模型分别为

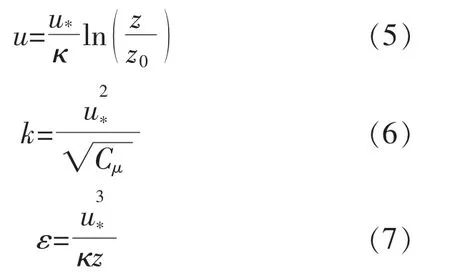
式中：u*为摩擦速度；κ 为冯卡门常数，取值为0.4；z 为离地高度；z0为大气粗糙度长度，表示近地层风速为零时的高度。

由本文提供的入口轮毂高度处的流场条件：风速 UREF（h）=6.5 m/s、湍流强度 IREF（h）=0.11，可得到：

式中：λ 为模型常数，对各向同性湍流取值为1.5。

出口边界设置为压力出口，左右侧面及上顶面设置为对称边界，地面采用标准壁面函数模拟，压力-速度耦合算法采用SIMPLE 算法，其他方程均采用二阶迎风格式进行离散。

2 计算域及网格划分

悬崖和高低山头地形的山体轮廓可由典型的对称山丘地形加以构造，而山丘地形的山体轮廓采用与大部分山体形状接近的余弦山体[10]。

图1 为悬崖和高低山头的地形轮廓图。对于悬崖地形陡坡面H/L1=2，缓坡面H/L2=0.2，H=40 m；对于高低山头地形考虑高度差Δh=10 m（高山在前）和Δh=-10 m（低山在前）两种工况，中心间距 d=200 m，H1/L1=H2/L2=0.4，低山 H1=40 m。

图1 悬崖和高低山头的地形轮廓Fig.1 Contour of cliff and high-low hill

对于悬崖地形，从计算域进口至迎风坡山脚9.5H 为上游，从背风坡山脚至出口15H 为下游，计算域大小为30H×15H×10H；对于高低山头地形，从计算域进口至前山山脚7.5H 为上游，从后山山脚至出口16.25H 为下游，计算域大小为35H×15H×10H。两种地形离散域的竖直方向网格划分均为100 个节点，底层网格为0.1 m，梯度比为2，在地形表面加密网格，再向外扩散，悬崖和高低山头地形的总网格数分别为500 万和540万。

3 结果及分析

3.1 致动盘模型验证

为了验证如上所述的致动盘模型和拓展k-ε湍流模型对于模拟风力机流场的准确性，采用位于平坦地形上的Nibe-B[11]风力机（风轮直径为40 m）作为验证对象，将其尾流速度的测量值作为验证数据。UREF 和湍流强度（IT）分别为8.5 m/s 和 0.11。

图2所示为三处尾流速度值 （x=2.5D，6D，7.5D）在径向方向上模拟值与测量值的对比。由图2 可知，模拟值与测量值吻合较好，尤其是在风轮轴线附近。由此结果可知，结合拓展k-ε 湍流模型的致动盘模型能较好地模拟风力机对流场的阻碍作用，可用于后续研究。

图2 致动盘模型验证Fig.2 Validation of actuator disk model

3.2 复杂地形绕流计算结果

针对悬崖地形，计算了陡坡迎风和缓坡迎风两种工况，计算结果分别如图3，4所示。图中（a），（b）分别为对称面（y=0）上的湍流强度云图和风加速因子的分布情况。

图3 陡坡迎风工况计算结果Fig.3 Calculation results on steep slopes

图4 缓坡迎风工况计算结果Fig.4 Calculation results on gentle terrain

对于陡坡迎风工况（图3）：风速在悬崖顶达到最大值，风加速因子明显，其值大于1；在悬崖背风缓坡上，随着与悬崖顶之间距离的增加，从缓坡x=50 m 的位置开始，近地面处的风加速因子值逐渐减小，风速衰减显著；远缓坡区（即x>100 m）存在明显的回流，湍流强度较大。因此，在排布风力机时，不宜将风力机布置在远离悬崖顶的缓坡上。综上，在接下来的研究中选择风力机安装在悬崖顶（x=0）和缓坡前半部（即 x=10，20，40，60，80 m 和 100 m）共 7 种布机方案。

对于缓坡迎风工况（图4）：随着高度增加，近地面的风加速因子值逐渐增加，说明气流在迎风缓坡上平稳加速，同时湍流强度维持低水平；风速在悬崖顶达到最大，但其风加速因子值小于陡坡迎风；由于背风坡坡度较大，背风坡及其下游的风速衰减显著，产生超过6H 的大范围回流区，湍流强度较高。因此，迎风坡和悬崖顶有利于排布风力机，而背风面反之。在接下来的研究中选择风力机安装在悬崖顶（x=0）和缓坡迎风区（即x=-10，-20，-40，-60，-80 m 和-100 m） 共 7 种布机方案。

针对高低山头地形，考虑低山在前和高山在前两种工况，计算得到对称面（y=0）湍流强度云图以及风加速因子分布情况（图5，6）。

图5 低山在前工况计算结果Fig.5 Calculation results of low hill ahead

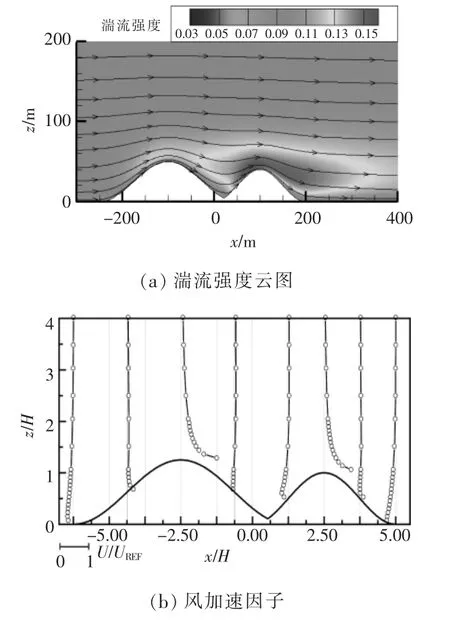
图6 高山在前工况计算结果Fig.6 Calculation results of high hill ahead

由图5 知：对于低山在前工况，高山和低山山顶风加速效应均显著，但高山山顶处的风加速因子更大，接近于1；山坳间有一个长约1.5H 的回流区，使其处于低速区中，风加速因子为负，回流区中的湍流强度迅速增大，一直延伸至高山山顶；高山背风面上存在较小的负风加速因子，风速衰减缓慢，并未形成流动分离，只存在小范围的低速区，湍流强度也保持低水平，若在高山后方布置风力机，仍需考虑合适的安全距离。因此，对于低山在前工况，选择风力机安装在高山和低山山顶两种布机方案。

由图6 可知： 高山山顶处的风加速效应更显著；高山背风面半山腰的风加速因子约为零，山坳间只形成了小范围低速区，且更靠近后山，并未发生流动分离；湍流强度在低山迎风面上增强明显，且高湍流区一直延伸至下风向约3H 的距离。如果在低山山头处布置风力机，需要考虑较高的湍流强度对风力机疲劳载荷的影响；若在低山后方布机，则需要考虑比低山在前更大的安全距离。因此，对于高山在前工况，选择风力机安装在高山和低山山顶两种布机方案，且对于低山山顶方案需重点关注湍流强度的大小。

3.3 风力机对典型复杂地形流场的影响

为探讨在典型悬崖和高低山头地形中有无风力机对功率预测的影响，我们提取了风轮前方1D处的风速剖面（图7）。图7 中两条点线用于指示风轮的上下界。悬崖地形选择陡坡迎风工况下缓坡x=10 m 的布机方案，高低山头地形选择高山在前且风力机布置在低山山顶的布机方案。

图7 风力机前1D 处的风速曲线Fig.7 Wind speed profiles at the front 1D of wind turbine

由图7 可知，有无风力机工况的风速剖面均在风轮前方1D 位置出现较大的速度差，布置有风力机的风速比未布置风力机的风速小，且差值区主要集中在风轮所在区域上下界。因此，在对复杂地形进行流场模拟和布机方案选择之后，有必要再进行风力机与复杂地形耦合流场的数值计算，以便获得更准确的风力机轴向入流风速和功率预测。

3.4 风力机入流特性分析

3.4.1 悬崖地形

表1，2 分别为在悬崖地形陡坡迎风和缓坡迎风工况下，由数值计算得到的各布机方案风轮前端1D 处的平均合速度、轴向入流平均风速、垂直风速分量、平均湍流强度以及由轴向入流平均风速得到的发电功率预测。

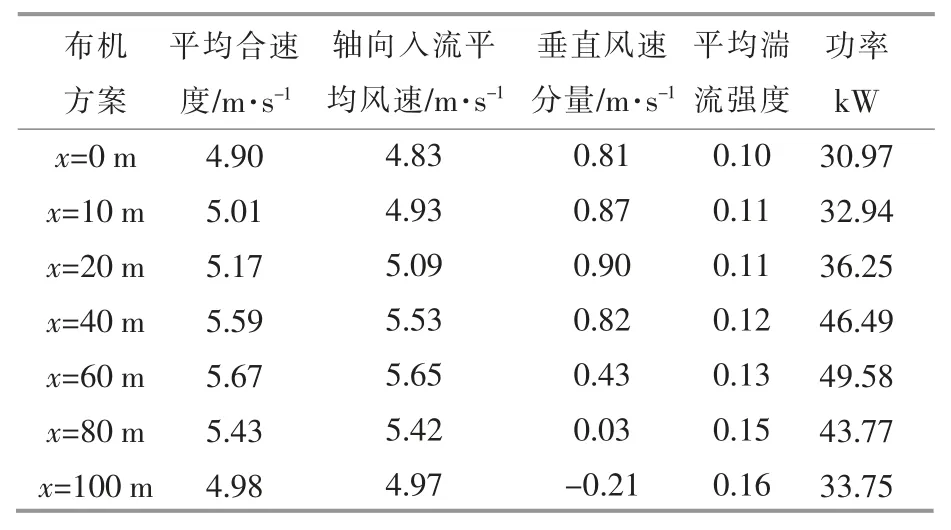
表1 悬崖地形陡坡迎风工况Table 1 Windward condition of steep slope

表2 悬崖地形缓坡迎风工况Table 2 Windward condition of gentle terrain

由表1 可知：在陡坡迎风工况下，山顶的轴向入流平均风速和功率预测并不是所有布机方案中最大的，其原因是陡峭的坡度使得气流在爬坡的过程中风速与水平方向形成较大的倾角，使得风轮前端的入流合速度在风轮轴向方向上的分量降低，从而影响了风能的吸收；在背风缓坡上，随着与山顶距离的增大，轴向入流平均风速呈现出先升后降的规律，而湍流强度逐渐上升，尤其是在缓坡半山坡以下（x>60 m），不仅轴向入流平均风速下降明显，湍流强度也显著增加，如前所述，这是由背风坡的流动分离和由此产生的涡旋所致。因此，这些位置不宜作为布机点。根据表1，对于悬崖地形陡坡迎风工况，综合考虑风速与湍流强度情况，建议将风力机安装在缓坡前部，在本例中即x=40～60 m。

由表2 可知，在缓坡迎风工况下，从缓坡半山坡（x=-100 m）开始，随着海拔高度的增加，轴向平均入流风速逐渐增加，风力机发电功率也随之增加，而湍流强度一直维持在正常水平。此外，受到缓坡地形轮廓的影响，即山体坡度由陡至缓，垂直风速分量相应地呈现出先升后降的发展规律。根据表2，对于缓坡迎风工况，为了捕获最大风能，建议将风力机安装在山顶附近。

3.4.2 高低山头地形

表3 为高低山头地形低山在前和高山在前两种工况，由数值计算得到的各布机方案风轮前端1D 处的平均合速度、轴向入流平均风速、垂直风速分量、 平均湍流强度以及由轴向入流平均风速得到的发电功率预测。

表3 高低山头地形Table 3 High-low hill terrain

由表3 可知，无论是低山在前还是高山在前，在高山山顶布置风力机时，轴向入流平均风速以及发电功率均最大，且高山在前工况略大于低山在前工况，而湍流强度值相差不大，均为正常水平。由于受到前山的阻塞作用，当高山在前时，后山 （低山） 的轴向入流平均风速小于低山在前工况，且湍流强度值更大，其值高于来流。根据表3，对于高低山头地形，最好将风力机布置在高山山顶，如果必须布置在低山山顶，最好选取低山在前工况。

4 结论

本文首先根据复杂地形绕流计算结果初步确定了一系列布机方案，然后采用致动盘模型和拓展k-ε 湍流模型相结合的方法，对悬崖和高低山头地形在不同来流工况下进行了若干组布机方案的地形与风力机耦合流场数值计算，通过对风轮前端1D 处入流风特性的分析，得出以下结论。

①对于悬崖地形：在悬崖陡坡迎风工况下，在山顶布置风力机并不是最佳方案，应当在靠近山顶的缓坡上布置风力机，在本例中为x=40～60 m；而在缓坡迎风工况下，随着海拔的升高，风力机出力也随之增加，在山顶布置风力机可以获得最大出力。

②在高低山头地形中，无论是低山在前还是高山在前工况，在高山山顶布置风力机均是最佳选择，若必须在低山山顶布置风力机，则应选择低山在前的工况。