带时间窗约束的集装箱空箱调运随机机会约束模型研究

石红国，高明瑶

SHI Hongguo, GAO Mingyao

（西南交通大学 交通运输与物流学院，四川 成都 611756)

0 引言

随着我国“一带一路”战略的实施，集装箱运输在我国社会经济发展中起着越来越重要的作用。由于我国生产力发展水平和自然资源分布不均衡，区域之间的贸易也呈现出不均衡性，最终造成集装箱运输过程中空重箱需求不均衡问题。为了解决该问题，需要在不同地区之间进行空箱调运。科学合理的调运方法能够压缩集装箱调运时间，降低调运成本，提高集装箱运输效率。通过深入分析集装箱空箱调运过程，研究集装箱空箱调运费用、运达时间的多目标综合优化方法。

近年来，随着集装箱运输的快速发展，很多学者对集装箱运输进行了一系列的研究。张得志等[1]对铁路集装箱空箱调度问题建立基于顾客偏好的运输规划模型和带时间窗的运输规划模型，并采用遗传算法对其进行求解；闫海峰等[2]充分考虑集装箱班列的开行特点，建立了混合箱流输送时间最少，距离最短，费用最低为优化目标的混合0-1 规划模型，并设计了二级耦合反馈系统算法进行求解；Song 等[3]针对动态和随机环境下的空箱配送问题，将其分成空箱装载和卸载2 个部分，分别制定配送策略，该方法在贸易不均衡时的求解结果明显优于传统的方法，降低了20%的成本；Chou 等[4]建立了混合模糊决策模型，将空箱配送问题分为两个阶段：模糊缺货存储模型和网络模型，优化各个港口之间的空箱调运问题；Cheung 等[5]针对带时间窗和带回程的车辆径路问题，建立了多属性标号匹配算法；Braekens 等[6]对满载集装箱和空集装箱的调运进行综合规划并采用启发式算法进行求解；Imai等[7]将单个集装箱卡车运输问题描述成0-1 线性规划模型，并设计了拉格朗日松弛算法对其进行求解；Jula 等[8]将单个集装箱接驳运输问题描述成带社会约束的带时间窗的非对称多旅行商问题，并基于动态规划和遗传算法的混合算法对其进行求解；Fischer 等[9]将铁路智能体系统应用于集装箱运输资源的调度中。

在上述研究中，各个铁路集装箱车站的集装箱需求量(供给量)均设置为确定值。而在实际应用中，集装箱供给和需求一般是不确定的，准确地估算集装箱调运数量能够降低成本，提高整个运输系统的运营效益。针对这种不确定的问题可以将集装箱需求量与供给量处理为服从一定分布的随机变量。在此基础上，以最小化集装箱运输费用和最大化集装箱到达时刻总体满意度为优化目标，构建带有时间窗约束的集装箱调运随机机会约束模型，通过将随机机会约束转化为确定性的等价类，将模型转化为对应的确定性模型，并设计基于TOPSIS方法和限定参数区间搜索的模型求解方法。

1带时间窗约束的集装箱调运随机机会约束模型构建

在整个铁路网中，存在多个集装箱站对集装箱有需求的情况，设D= {D1，…，Dn}为集装箱需求站；同时也存在多个集装箱站能够供给集装箱，设S= {S1，…，Sn}为集装箱供给站。为便于模型描述，在此对变量统一定义，变量定义如表1 所示：

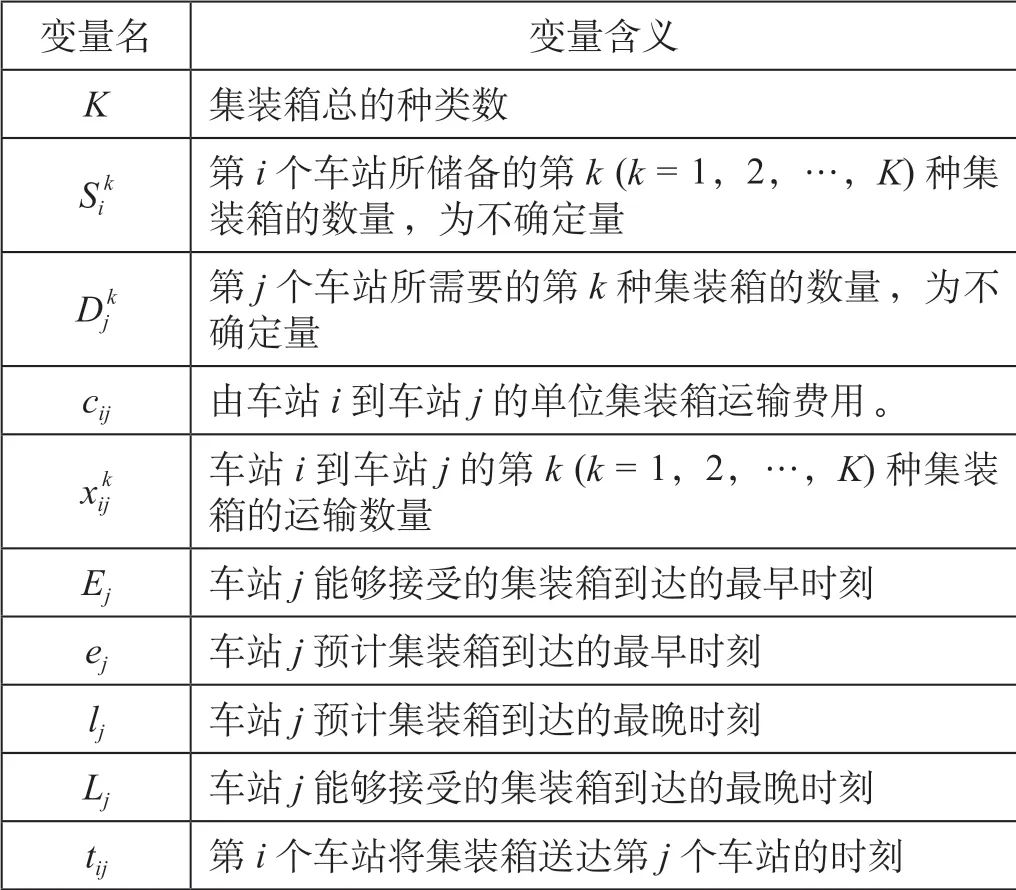
表1 变量定义Tab.1 Variables definition

在实际的集装箱运输问题中，如果集装箱过早到达，则需要在目的地进行等待，降低了集装箱的运用效率；如果集装箱到达过晚，则会影响其他的货物运输，引起损失，因而集装箱的到达时刻应在一定范围内，可考虑利用函数来描述这种时间限制。集装箱调运到达时刻满意度如图1 所示。

用函数μij(tij)来描述上述集装箱到达时刻满意度，如公式 ⑴。

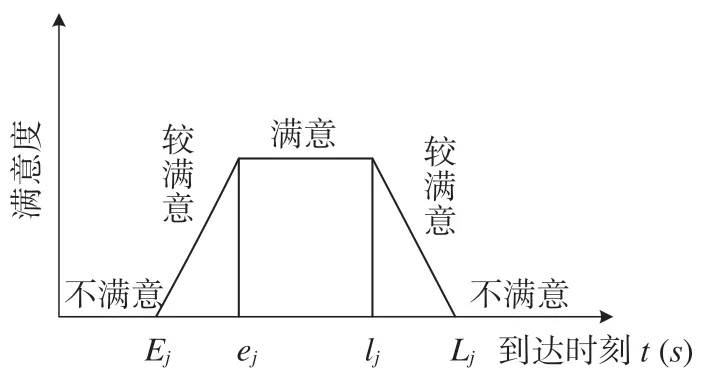
图1 集装箱调运到达时刻满意度Fig.1 Arrival time satisfaction of container transportation

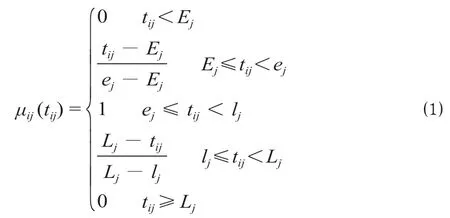
以最小化集装箱运输费用和最大化集装箱到达时刻总体满意度为优化目标，考虑车站的集装箱供给量与需求量的不确定性，构建带有时间窗约束的集装箱调运随机机会约束规划模型如下。

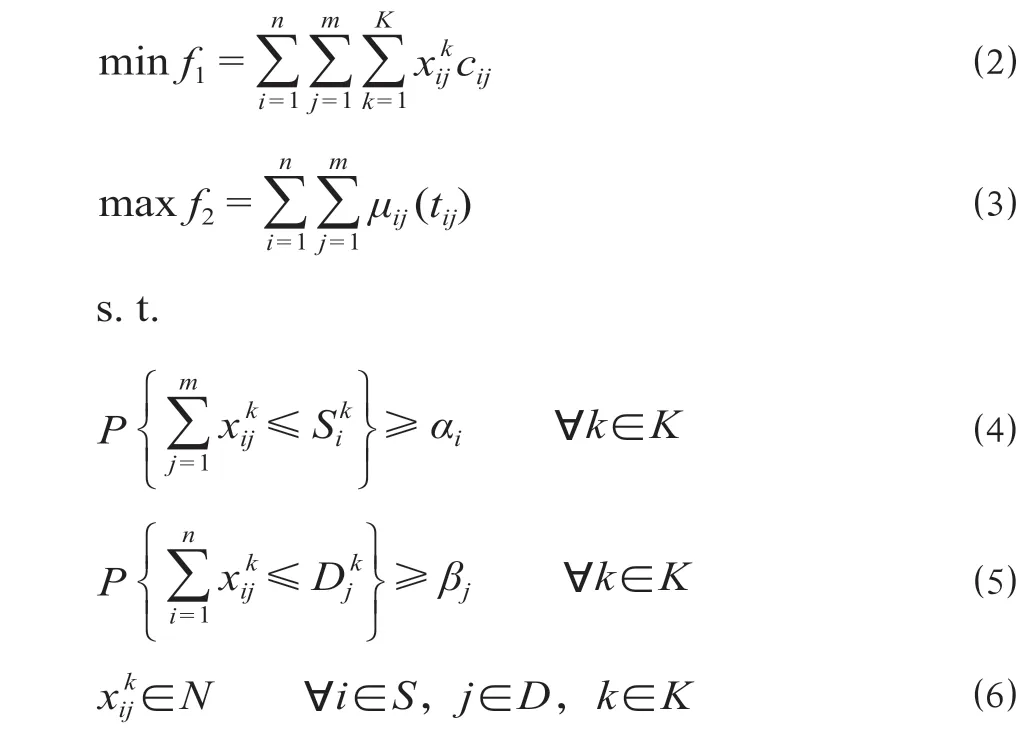
式中：αi，βj分别表示供给与需求满足的概率；N为正整数集合。

公式 ⑵ 表示最小化总的集装箱调运费用；公式⑶ 表示最大化集装箱总体调运满意度；公式 ⑷ 表示车站i的第k种集装箱供给量发生变化时，从车站i到车站j运输的第k种集装箱的数量小于等于车站i的第k种集装箱供给量的概率在αi以上，即车站i的第k种集装箱供给量发生变化时的机会约束条件成立的概率在αi以上；公式 ⑸ 表示车站i的第k种集装箱需求量发生变化时，从车站i到车站j运输的第k种集装箱的数量小于等于车站j的第k种集装箱需求量的概率在βj以上，即车站j的第k种集装箱需求量发生变化时的机会约束条件成立的概率在βj以上；公式 ⑹ 为对变量取值的约束。

2集装箱空箱调运随机机会约束模型求解

2.1 不确定性变量的处理

当各车站的需求和供给量为确定值时，集装箱的调运问题即转换成运输问题，采用表上作业法进行求解。当各车站的需求和供给量为不确定值时，即对于第2 节建立的随机机会约束模型，可以考虑将其转换成一个确定的等价类模型。

设随机变量Sik服从正态分布N(μi，σi2)，将其分布函数代入公式 ⑷，可得公式 ⑺。

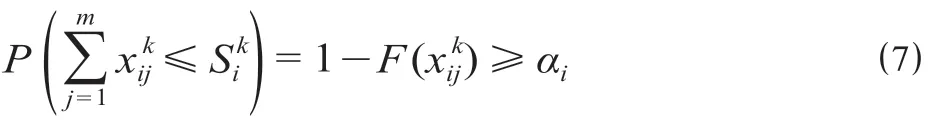
式中：F(*)表示分布函数。

公式 ⑺ 将不确定的概率表达式转化为常规不等式。对公式 ⑺ 进行标准化，得

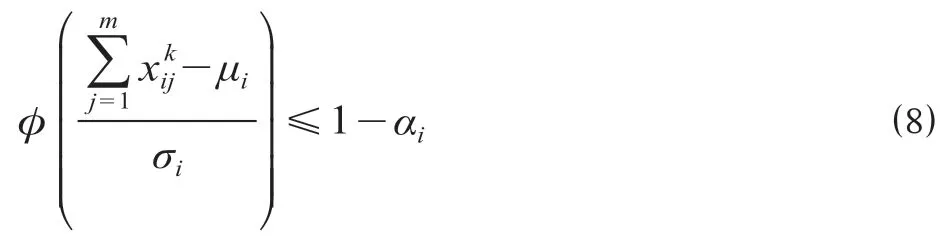
对公式 ⑻ 两边取反函数，得公式 ⑼。

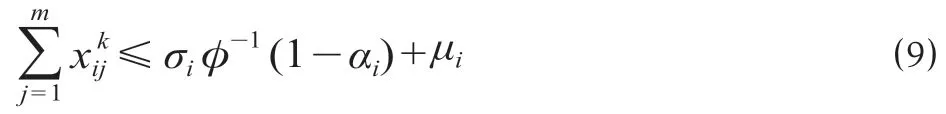
同理，可得

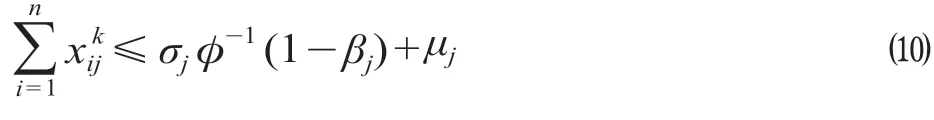
利用分布函数的相关知识做上述不等式化简，可以得出关于两地集装箱运输量的限制条件，为模型的求解奠定基础。

2.2 多目标模型的非劣解择优

TOPSIS 方法根据有限个评价对象与理想化目标的接近程度进行排序，在现有的对象中进行相对优劣的评价，是多目标决策分析中常用的有效方法。为此采用TOPSIS 方法评价方案。

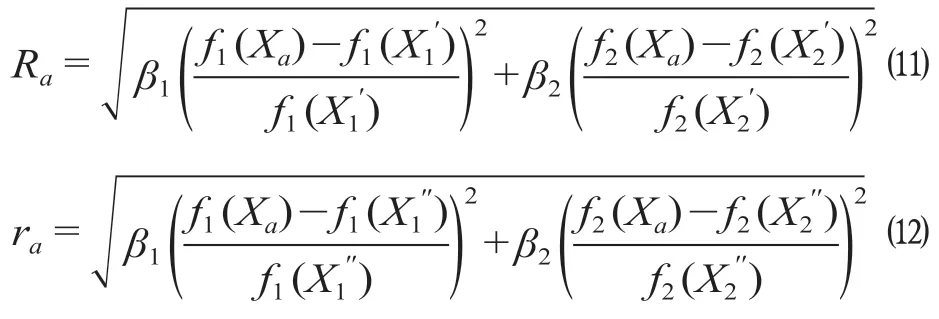
式中：β1，β2分别为关于集装箱调运的总的调运费用与总体到达满意度所占的权重，且β1+β2= 1；f1(Xa)为方案Xa的集装箱调运总调运费用；f2(Xa)为方案Xa的集装箱调运总体满意度。

则方案Xa对理想点的相对接近度εa为

εa越大，方案越优。

2.3 限定范围的帕累托最优解搜索算法

非劣解是满足帕累托最优条件的解集中的向量。多需求站，多供给站，多集装箱种类的集装箱调运问题属于具有复杂、不连续的帕累托前沿的多目标优化问题，其非劣解的数量，将随系统内需求站，供给站和集装箱种类的增加而呈几何级数增长。为有效减少计算量，提高计算效率，采用一种限定参数区间的帕累托最优解搜索方法进行模型求解。

选择总调运费用为限定参数。若限定调运费用不超过某值，则定义该值为限定调运费用，用表示。设调运总费用单目标模型对应的最少调运费用为，调运总体满意度最大单目标对应的最少调运费用为，则可以将非劣方案的调运费用限定在闭区间[，]，由于＜方案是实际不可行的方案，而＞的方案对应的费用不少于总体满意度单目标模型最优解，显然也为较劣解。当＞时，不考虑该方案，令所有的为0，并将该约束加入总体满意度最大单目标模型。求解费用在[，]之间，且满意度最大的非劣解，确保得到的帕累托最优解均在帕累托前沿，并通过与理想点的相对接近度确定最优方案。具体求解步骤如下。

（1）不考虑目标函数公式 ⑶，以目标函数公式 ⑵为单优化目标，求解公式 ⑵ 对应的最优解，即最少调运总费用。

（2）不考虑目标函数公式 ⑵，以目标函数公式 ⑶为单优化目标，求解公式 ⑶ 对应的最优解，即最大调运满意度。

（5）比较所有方案对理想点的相对接近度，选出最优方案。

限定参数区间的帕累托最优解搜索算法，能在求解大规模问题时，减少最优解的搜寻次数。

3算例分析

3.1 参数设置及模型处理

设某铁路区域共有4 个集装箱供给站S1，S2，S3，S4，4 个集装箱需求站D1，D2，D3，D4。车站集装箱供应数量分布情况如表2 所示，表中数据表示各个集装箱供给站集装箱供给量的分布函数，例如，在表2 中，供给量参数S11服从均值为20，方差为2 的正态分布N(20，2)。车站集装箱需求数量分布情况如表3 所示，表3 中数据表示各个集装箱需求站的集装箱需求量的分布函数，具体含义与表2 类似。车站间的集装箱单位调运成本如表4 所示，表中数据表示各个集装箱供给站到各个集装箱需求站的单个集装箱的运输费用。

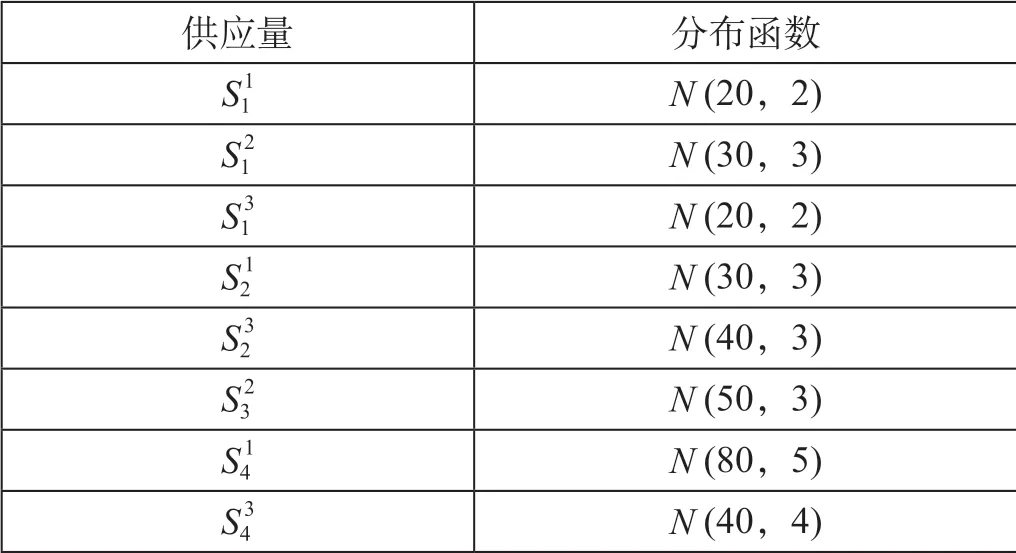
表2 车站集装箱供应数量分布情况Tab.2 Distribution of container supply quantity at station

设供给站i将集装箱送达时刻tij分别为12 : 00，15 : 30，15 : 00，15 : 20。需求站j的集装箱预计的最晚到达时间lj为15 : 00，16 : 00，14 : 20，15 : 30。lj与Lj之间间隔30 min。置信水平αi，βj均取95%，

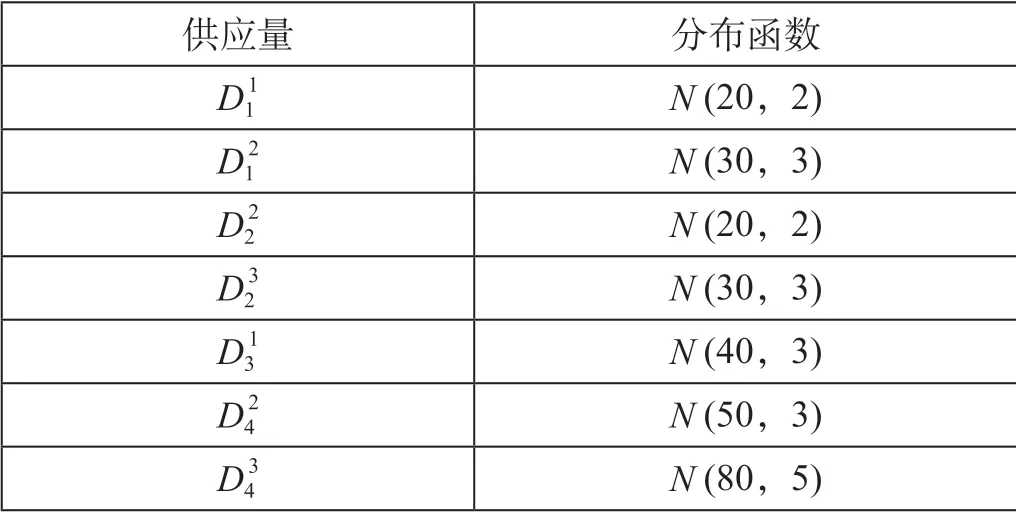
表3 车站集装箱需求数量分布情况Tab.3 Distribution of container demand quantity at station

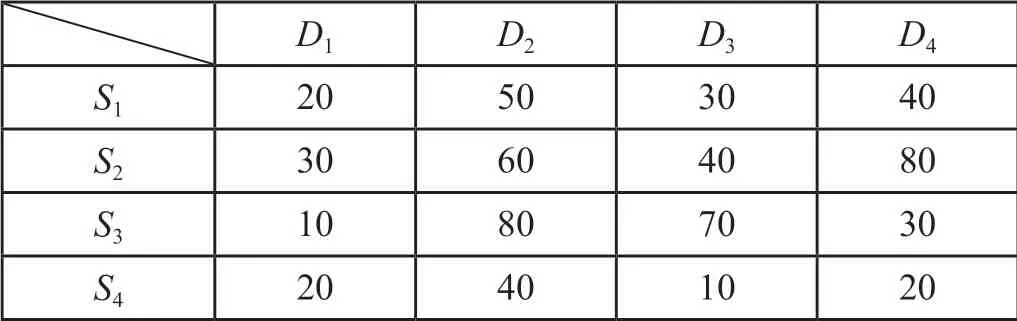
表4 车站间的集装箱单位调运成本 百元/TEUTab.4 Container unit transfer cost between stations

则

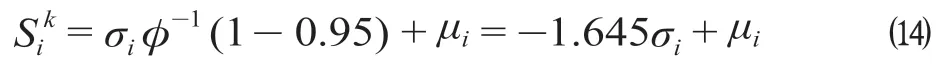
计算可得S11= -1.645×2 + 20 = 16.71，取整可得S11= 16。同理，处理其他随机变量，得到各个车站的供给量和需求量分别为：

3.2 求解与分析

利用MATLAB中的GUROBI优化软件对集装箱调运费用最小单目标模型进行求解，得到最优解X1′和最劣解X1′′；对集装箱总体到达满意度最大单目标模型进行求解，得到最优解X2′和最劣解X2′′，其对应的目标函数值分别如下。

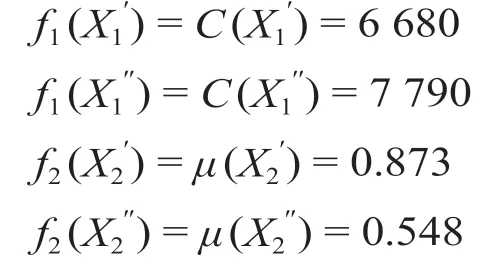
考虑到运输费用和集装箱到达满意度在集装箱调运系统中占的比重，取权重系数β1为0.6，β2为0.4。按公式(11)—(12)分别计算不同的方案与正负理想点的相对距离Ra和ra，按照公式 ⒀ 计算和理想点的相对接近度εa，最终得到的最优方案X*的总费用与总满意度为

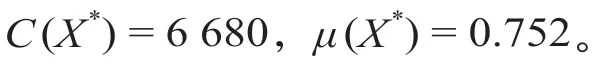
如果αi=βj= 100%，则问题转换为确定性问题，即可用表上作业法进行求解。集装箱需求/供给量确定情形与不确定情形下的集装箱调运结果对比如表5 所示。

表5 集装箱需求/供给量确定情形与不确定情形下集装箱 调运结果对比Tab.5 Comparison between the certain and uncertain amount of container demand (supply)

由表5 可知，与确定性情形相比较，不确定情形下的集装箱调运总费用由7 120 减少为6 680，降低了6.2%，总体满意度由58.7%提高为75.2%，提高了16.5%。综合考虑需求/供给量不确定性、集装箱调运总费用与总体满意度，最优调运方案如表6 所示。表6 中数据是各个集装箱供给站到各个集装箱需求站的最优供给量。例如，表中第1 个数据16 表示第1 个集装箱供给站S1到第1 个集装箱需求站D1的第1 种集装箱的最优供给量为16 TEU。

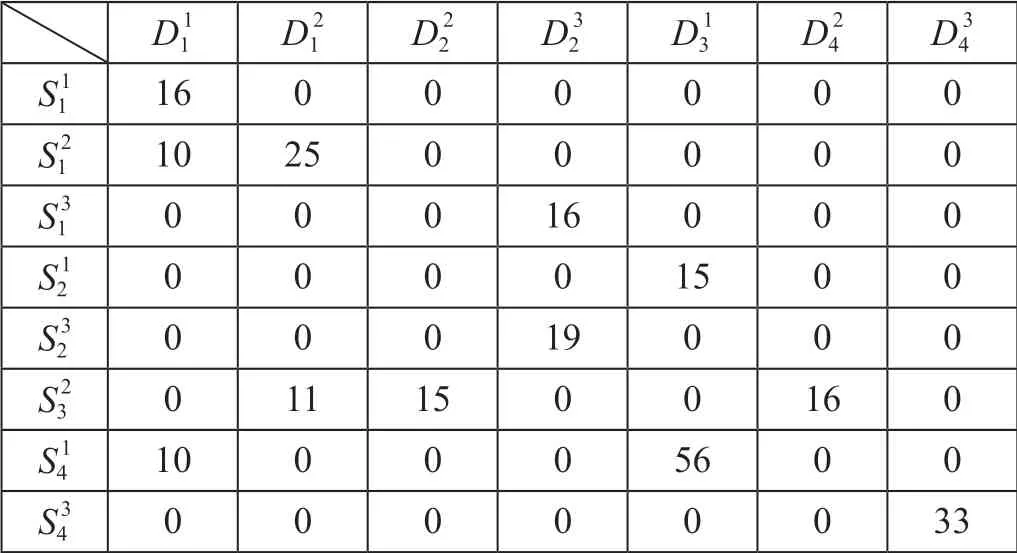
表6 最优调运方案 TEUTab.6 Optimal container transfer plan

4结束语

近年来，集装箱运输在我国经济发展中扮演着举足轻重的作用，解决集装箱空箱调运的均衡问题成为重中之重。合理分析完善集装箱运输过程，提高集装箱运输效率，可以使得集装箱运输发挥更大的经济效益。在整个集装箱运输问题中，涉及到的因素比较多，主要包括如何使集装箱运输时间最短，运输费用最低，到达时间方面的约束，出发时间的约束，集装箱存储问题，接驳问题，空箱调运问题等，这些问题的妥善解决将有助于稳固与发展集装箱在国民经济中的作用。