下承式空钢管系杆拱桥结构稳定性影响研究
2020-02-25宋力锋
宋 力 锋
(福建农林大学 金山学院,福州 350002)
随着桥梁事业的发展,空钢管拱桥的应用在桥梁建设工程中也逐步增多,但是其力学特征特别是动力稳定性方面与目前应用较为广泛的钢管混凝土拱桥有所不同[1].本文以实际跨河下承式空钢管拱桥工程项目为背景,采用有限元软件ANSYS建立空间模型研究其正常使用工况下的失稳特性,并通过对宽跨比、横向联系、吊杆损伤这三个参数分析,研究其对下承式空钢管系杆拱桥结构稳定性的影响,得到一些与该类桥梁稳定性相关的建议[2-3].
在充分认识到自己的职业范围、职业形式、自我兴趣和能力等后,需要制定一份职业生涯的规划,作为自己人生目标的规划线,研究自己适合的职业、自己适合从事的职业岗位、社会迫切需求的职业、预测工作范围的变化情况、不同工作对自己的要求及应对措施、预测可能出现的竞争、如何相处与应对人和事等,要想更好的去完成自己设定的规划,职业的路上再根据自己的职业生涯变化不断调整自己的职业生涯规划。
1 下承式空钢管系杆拱桥有限元模型
1.1 工程背景
某下承式空钢管桁肋系杆拱桥全长为188.63 m,主拱为净跨径97.75 m的下承式桁肋系杆拱,桥面宽:[1.35 m(管道支架)+0.8 m(检修通道)+1.35 m(管道支架)]=3.5 m,矢高19.95 m,矢跨比1∶4.9,而该桥的宽跨比非常小,约为1∶28;两边引桥采用两跨连续钢桥,边跨标准跨径为:21.13 m+19.92 m(往粉煤灰综合利用厂区方向);19.92 m+22.20 m(往电厂方向).拱肋除拱脚段填充混凝土外,其余均由空钢管构成.设计荷载包括检修荷载、管道支架荷载、粉煤灰运行荷载、电缆桥架荷载(见图1、2).
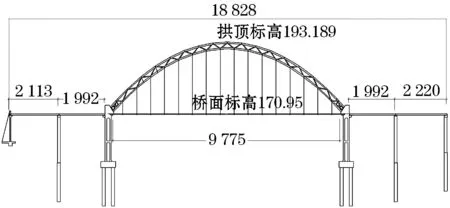
图1 跨河桥梁立面图
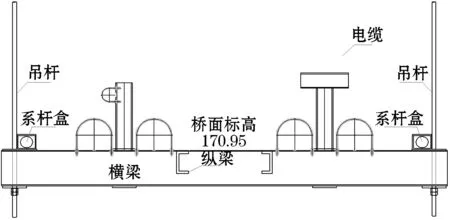
图2 主拱桥桥面系横向布置图
1.2 拱桥有限元模型
该跨河拱桥稳定性分析仿真过程采用Ansys软件模拟,先建立节点、单元,全桥组合创建下承式空钢管系杆拱桥有限元模型[4-5].其中拱桥弦杆、腹杆、平联杆,纵、横梁以及斜撑、系杆、吊杆、墩台等各部件采用Ansys软件BEAM44单元和LINK10单元建立,最终形成418个节点,708个单元组成的三维空钢管拱桥模型[6].(见图3)
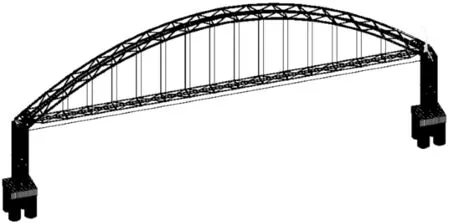
图3 主拱桥有限元模型图
对于拱桥而言,由于在自重作用下会发生结构的竖向沉降,进而使得实际结构与设计的拱轴线型以及主梁标高产生差异,因此在施工前就应该事先考虑如何抵消重力的影响,使得结构在重力作用下最后保持的形状与期望的形状一致[7].本文采用在恒载及半活载作用下调节系杆和吊杆的预加力,这样同时兼顾了不加载和加载后拱桥的受力情况.调节吊杆预应力的原理是通过调节吊杆中的应变来调节桥面梁的位移,而对系杆的调节,除了要平衡拱桥墩间的推力作用外,还要考虑系杆力对拱桥标高的影响,最后通过对吊杆与系杆间的多次迭代调节,使得构件变形在规定的范围之内[8-9].从图4、5中可以看出本例中的小宽跨比下承式空钢管桁肋系杆拱桥经过多次迭代调整后,从模型的静力计算结果可以发现拱桥桥墩墩顶的纵向位移以及吊杆下端的竖向位移基本趋向于零,拱桥的预加力调整结束,有限元模型建立完成.
图4 纵向位移图

图5 竖向位移图
2 稳定性分析
通过施加正常运营情况下的荷载,对该下承式空钢管系杆拱桥结构模型的稳定性进行分析研究,提取其前10阶稳定系数、失稳模态以及屈曲模态(如表1).
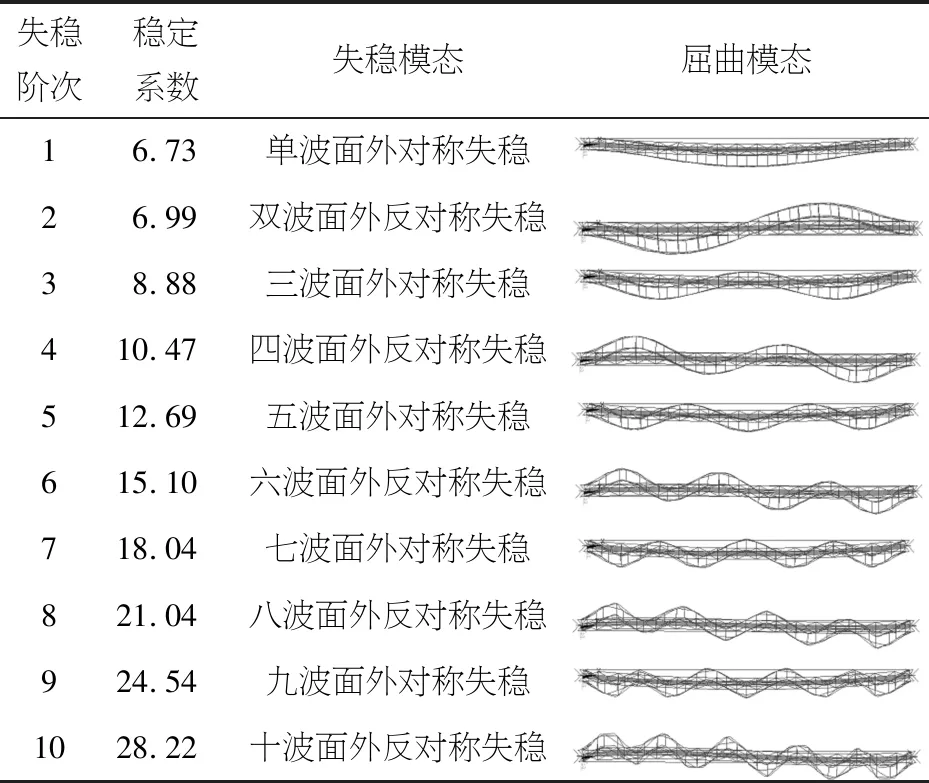
表1 正常使用工况下拱桥稳定系数及失稳模态
宽跨比是指桥梁桥面宽度与跨径之比,本文的桥面宽度采用的是两相对吊杆之间的间距.建模采用的拱桥宽跨比为1/28,而《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTGD62-2004)》规定当拱桥的宽跨比小于1/20时,需要验算拱的横向稳定性,可以看出宽跨比这一参数对本文中拱桥的稳定性分析有较大影响[13].本文拱桥结构模型模拟宽跨比参数影响是不改变拱桥的跨径L,通过变化拱桥两相对吊杆间的间距D来调整拱桥的宽跨比,拱肋间的横向联系方式以及边界的处理与原模型相同.采用不同宽跨比建模进行恒载作用下的稳定屈曲分析,计算结果如表2及图6所示.
3 影响拱桥稳定性参数分析
工况2:去除拱肋上弦杆间的所有平连杆;
3.1 宽跨比对空钢管桁肋系杆拱桥稳定性的影响
从表1结果可以看出,拱桥稳定系数值随着失稳阶次增加而增大.根据相关稳定性分析理论,若拱桥第一阶稳定系数小于4~5,则结构偏于不安全,反之,则拱桥结构较为安全[10].而表1中的该下承式孔钢管系杆拱桥第一阶稳定系数为6.73, 大于4, 这表明该空钢管拱桥从结构稳定性角度考虑较为安全.另外,该拱桥模型前10阶的失稳模态和屈曲模态图均体现出各波面外对称或面外反对称失稳, 说明此下承式空钢管桁肋系杆拱桥的面内外刚度相比较,拱桥的面外刚度不足[11-12].
优化教堂广场的空间属性,从目的上讲,即使教堂广场空间成为除具有文化优势外,同时又具有交通优势与视域优势的优质空间,促进更多的人可以到达或经过广场,提高空间活力.而从理论上讲,提高人进入广场的可能性,应提高空间的可达性与可见性.
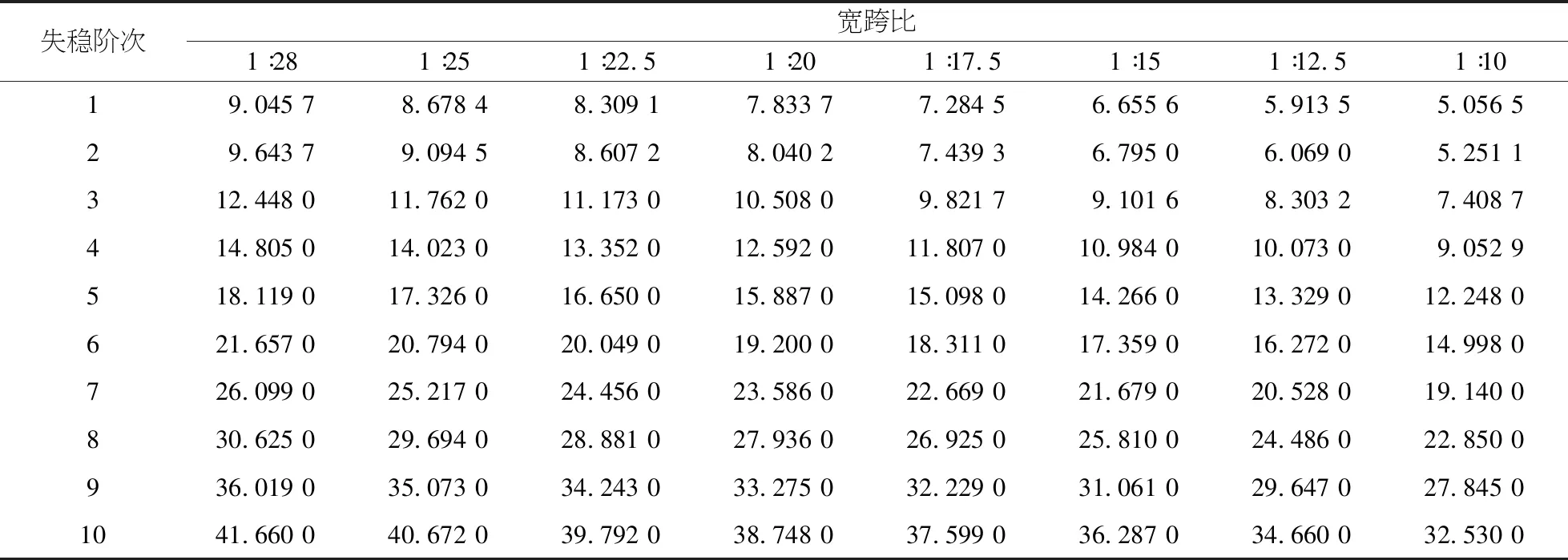
表2 宽跨比不同工况下拱桥稳定系数

图6 宽跨比不同工况下下承式空钢管系杆拱桥稳定系数对比图
常用的过氧化试剂有过氧甲酸、过氧乙酸、间氯过氧苯甲酸等。过氧酸是一种酸性比母体酸若千倍的弱酸,造成这一现象的原因主要是过氧酸分子内极易形成能量稳定的五元环所致。不过这不代表安全,长链过氧酸室温为固体,较为稳定。而短链液体过氧酸,受热易分解和爆炸,应避光低温妥善保存。过氧酸常常被用作引发剂、氧化剂[15]和消毒剂。
环偶极子以其独特的电磁特性与太赫兹波相结合,在太赫兹透明材料、吸波器、滤波器等功能器件上应用广泛。本文所提出的平面型太赫兹环偶极子超材料为环偶极子的后续研究提供了实验基础,为柔性环偶极子超材料的研究提供了一种新的思路。
3.2 横向联系对空钢管桁肋系杆拱桥稳定性的影响
本文原先小宽跨比下承式空钢管桁肋系杆拱桥模型的横向联系方式为对应拱肋的上、下两根弦杆分别通过两排空钢管平连杆相连.下面研究拱桥横向联系布置对其稳定性的影响,即改变弦杆间平连杆的布置,通过以下几种处于恒载作用下的工况进行稳定屈曲分析[14]:
工况1:去除拱肋上、下弦杆间的所有平连杆;
通过上文对小宽跨比下承式空钢管桁肋系杆拱桥稳定屈曲的计算,知道该桥的面外刚度较弱,容易发生面外失稳.目前,对于此类小宽跨比空钢管拱桥的研究还比较少,尚没有形成成熟的理论,因此,本文将探讨桥梁的宽跨比、横向联系布置形式、吊杆损伤等结构参数变化对其稳定性的影响.
工况3:去除拱肋下弦杆间的所有平连杆;
该矿体是槐树坪金矿区主要的矿体之一,严格受F29断裂控制,沿走向控制长度760m,沿倾向控制最大斜长710m,埋深约0~684m。走向330°~350°,倾向北东,倾角75°~87°,矿体最高金品位达9.06×10-6,平均品位为4.00×10-6,品位变化系数为68%,属均匀型,品位随倾向和埋深呈低-高-低特征;厚度为0.46~9.11m,平均厚度1.54m,厚度变化系数为110%,属较稳定型,其变化特征为倾角变陡,厚度变厚,倾角变缓,厚度变薄,沿倾向随着深度变化矿体呈薄-厚-薄特征;矿体形状总体呈不规则状,多处无矿边界为港湾状。
工况4:原实际拱桥模型;
在下承式系杆拱桥中,桥面板的恒载以及后期运营时的活载作用都是通过吊杆传递到拱肋上的,再由拱肋传递到桥台上的,因此吊杆对于此类桥梁来说至关重要.本桥模型采用竖直吊杆,双侧对称布置,单侧为16根吊杆,全桥32根吊杆共同作用.拱桥经常会遇到汽车超载以及应力腐蚀导致吊杆受损的情况,下面通过假设吊杆不同受损情况分成5种工况来模拟其对拱桥稳定屈曲的影响[15]:
那年,她和同事去济南检查安全生产。那是一家部里直管的化工企业。她记得,雷志雄的表舅,在这家厂里当副厂长,估计是表舅出面把雷志雄调回济南的。一打听,雷志雄是一个分厂的副厂长了。这次到济南出差是她争取的,当时安排她去兰州,她找到主管副总,要求到济南。她想念雷钢和雷红。
工况6:在原拱桥模型拱肋的上弦杆间增加X撑作用;
本文简单介绍了基于Mesh架构的无线传感器网络的概念和原理,并利用ZigBee,ARM,VC++等技术研发构建了基于MESH架构的无线传感器网络监控系统,实现对育苗温室群内环境信息的精确采集、实时监测和远程调控等功能。本文详细介绍了基于MESH架构的无线传感器网络监控系统的结构、无线传输节点的元器件选型及开发原理、总控计算机的选型、系统管理软件的设计思路及开发原理,并对搭建的无线传感器网络监控系统进行实际运行测试。测试结果表明,系统能够准确完成工厂化育苗过程中温室环境的远程无线监测与自动调控。
工况7:在原拱桥模型拱肋的上、下弦杆间均加上X撑作用;
从表3以及图7中不同横向联系下的小宽跨比下承式空钢管桁肋系杆拱桥的稳定计算结果可以看到在工况1时,结构去除所有平连杆作用,拱桥结构的第一阶稳定系数低于规范上对于一阶稳定系数要大于4~5的规定;在工况2和工况3中分别去除模型的上、下平连杆后,其稳定系数均较原模型来的低,但还是满足规范对结构第一阶稳定系数的要求,其中去除上平连杆后稳定系数比去除下平连杆后的稳定系数要低,这表示上弦杆之间平连杆对拱桥的横向稳定作用更明显;工况6和工况5分别在原模型的上、下弦杆上增加X撑,其稳定安全系数与原模型相比大大提高,而在上弦杆上增加X撑比在下弦杆上增加X撑的稳定安全系数增大更多,这也表明了在上弦杆之间的横向联系对提高拱桥的横向稳定性作用更大;对比工况6和工况7发现,上下弦杆间全部施加X撑与仅在上弦杆上增加X撑其第一阶稳定安全系数相差不大,而是从第二阶开始其稳定系数开始相差不断增大.由于拱桥的稳定屈曲主要关注其第一阶的稳定安全系数,所以若要增大拱桥的安全储备,从实用性和经济性上来说可以只增加拱肋上弦杆之间的横向联系.

表3 不同横向联系工况下拱桥前10阶稳定系数

图7 不同横向联系工况下拱桥前十阶稳定系数对比图
原拱桥模型的第一阶失稳模态为面外对称,从以上对拱桥模型的横向联系布置情况来看,增加拱肋间的横向联系可以增大拱桥的稳定安全系数,加强拱桥的稳定性.但是对于本例空钢管下承式桁肋系杆拱桥而言,其面外刚度依然偏弱,各工况下的第一阶失稳模态均为面外对称失稳,这说明仅通过改善横向联系对拱桥面外刚度的帮助还稍显不足.
从表2以及图6可以发现在原拱桥模型的基础上,将拱桥结构的宽跨比从1∶28逐渐增大到1∶10,空钢管下承式桁肋系杆拱桥的各阶稳定安全系数不断减小,结构第一阶稳定安全系数均满足规范上大于4~5的要求,拱桥在不同宽跨比下的第一阶屈曲失稳模态均表现为面外对称失稳.从分析结果上可以判断,对于本例中横向联系较小的空钢管桁肋系杆拱桥而言,加大拱桥的宽跨比,使得桥梁拱肋间的平连杆长度增加,减弱了桥梁间的横向刚度,因此拱桥的横向稳定性也随之降低.
3.3 吊杆损伤对空钢管桁肋系杆拱桥稳定性的影响
工况5:在原拱桥模型拱肋的下弦杆间增加X撑作用;
工况 1:原空钢管拱桥模型;
工况2:去除原拱桥模型单侧拱肋1/2处吊杆;
工况3:去除原拱桥模型双侧拱肋1/2处吊杆;
工况4:去除原拱桥模型单侧拱肋1/4、3/4处吊杆;
工况5:去除原拱桥模型双侧拱肋1/4、3/4处吊杆;
从表4和图8中可以看到局部吊杆处于不同损伤工况下时,对拱桥稳定安全系数产生的影响非常微小,拱桥第一阶的稳定安全系数最大变化率仅为0.23%,而其在前10阶范围内的最大稳定安全变化系数变化率也仅达到0.27%,可见局部吊杆损伤对该下承式空钢管桁肋系杆拱桥的稳定性影响很小.

表4 不同吊杆损伤工况下拱桥前10阶稳定系数

图8 不同吊杆损伤工况下拱桥前10阶稳定系数对比图
4 结 语
本文通过对建立的下承式空钢管桁肋系杆拱桥的ANSYS有限元模型进行正常运营工况下的结构稳定性分析,从稳定系数,失稳模态和屈曲模态的结果体现了该桥的面内刚度大于面外刚度,容易发生面外失稳.在进一步分析该拱桥模型在不同结构参数下的稳定屈曲模态时表明,对本文中的下承式空钢管系杆拱桥而言,仅增大拱桥的宽跨比,会相当于加大了拱肋间平连杆的长度而使得拱桥的横向刚度减小,横向稳定性减弱;加强拱肋弦杆间的横向联系可以较大程度的提高拱桥整体稳定性,特别是上弦杆间的横向联系的效果显著;局部吊杆损伤对拱桥的稳定性影响较小,而单侧吊杆受损与双侧对称吊杆受损相比影响更大.
