基于惩罚Logistic回归的多元统计过程控制研究

钟琦君

(天津大学管理与经济学部,天津 300072)

在现代制造业和服务业中,传统控制图无法有效处理高维度且分布未知的复杂数据,人们经常用多元控制图同时监控过程中的多种质量特性。多元控制图的基本任务就是监控均值向量μ是否发生改变,即偏移;识别均值向量μ何时发生偏移;识别并隔离发生偏移的变量。通常此类问题会假设:

H0:x1,x2,…,xt～Nm(μ0,∑),

H1:x1,x2,…,xτ-1～Nm(μ0,∑),

xτ,…,xt～Nm(μ1,∑)。

在τ时刻均值向量发生偏移。传统控制图为了解决这个问题,先假设观测向量Xi=(x1i,x2i,…,xmi),当i=1,2,…,τ-1时服从正态分布Nm(μ0,∑),当i=τ,…,t时,服从正态分布Nm(μ1,∑),其中μ0和∑已知,μ0≠μ1。假设协方差矩阵不发生偏移,因此可以用样本协方差矩阵S代替假设中的总体协方差阵∑,此时得到HotellingT2统计量[1]。基于该统计量,多种多元统计过程控制图(MSPC,multivariate statistical process control)的控制图被提出:累计和的多元控制图(MCUSUM)、指数加权平滑的多元控制(MEWMA)图、U2多元控制图[2-9]。这些方法的监控统计量和控制限的计算需要假定该过程服从多元正态分布。然而,在实际应用中,正态假设很难满足,从而会影响控制图的性能。在当下的控制图应用场景中,复杂高维数据的问题,非高斯分布的受控数据集的问题,类别变量、混合变量和缺失数据的问题,数值变量的不同取值范围问题引起了广大学者的关注。因此,也有研究指出需要提出不依赖受控数据分布假设的非参数控制图[10-14]。在对高维数据进行监控时,传统的MSPC对变量的小幅偏移敏感,因此功能更强大的控制图需要被提出来。

为了解决上述问题,最近有些研究者将机器学习的方法应用在了MSPC的问题中。Hwang等[15]将监控问题转变成了一个监督式学习的问题,人为的生成失控数据,将参考数据集标记为一类,人工数据标记为另一类,训练出分类器,将控制图的问题转化成了二分类的问题,再通过训练好的分类器把将来的观测数据分为受控或失控。此类做法统称为one-class的分类方法在控制图中的应用,类似如Sun等[16]提出的基于支持向量数据描述(SVDD)算法的控制图,Sukchotrat等[17]提出的基于k-近邻算法的控制图都是基于one-class分类方法的控制图。在one-class的模型里面存在的一个问题是,分类器是早就建立好的,要么根据人工数据,要么根据某种具体的one-class模型,后续观测到的数据只是通过该分类器进行归类,因此分类器是没有用到实时观测值的任何信息的,这大大降低了控制图的准确性和敏感性。因此Deng等[18]提出了依据现代机器学习生成模型的快速性,来构建实时生成分类器的控制图以提高监控性能,该方法被称作RTC(real time contrast)方法,作者提出的是基于RTC的随机森林方法控制图。也有学者提出了基于RTC的核线性判别方法的控制图[19]和基于RTC的SVM控制图[20]。

在面对高维数据的控制图研究中,特征提取同样是值得关注的问题,在生物统计领域很多学者将特征提取与机器学习结合使用,来找出人体庞大基因库中与特定疾病有关的基因。其中Shen等[21]通过基于Lasso惩罚的Logistic回归对基因数据进行降维,辨别基因库中与白血病有关的基因。机器学习相关研究发现在针对复杂关系的高维数据时,线性分类器例如Logistic回归能带来比SVM方法更好的拟合和分类表现。

综上可见,随着传感器的引入,收集到数据的维度越来越高,传统的MSPC对高维数据中只有少数变量偏移的过程监控是不敏感的。一般的控制图都会假设先验分布,但在高维数据情形下,受控数据样本有限,其分布往往是难以估计的,因此需要提出不依赖受控数据分布假设的控制图。基于非参数检验的控制图虽然可以解决分布估计问题,但是无法解决复杂计算过程的问题。引入机器学习的分类器,通过RTC方法,将监控问题转化为对观测数据进行实时分类的过程,实现对高维数据的有效监控,不需要先验分布,计算高效且精确;引入Lasso可以进行特征提取,提高控制图的敏感性,有利于报警之后快速诊断失效因素。

因此研究提出基于Lasso的Logistic回归模型来建立控制图,采用RTC方法进行监控设计,为了方便简称该控制图为RTC-LR。

1 惩罚Logistic回归

1.1 Logistic regression

在实际生成过程中,假定过程的m维测量值Xi=(x1i,x2i,…,xmi),其中i=1,2,…,相当于产品生产过程中监控到的质量特性值。响应变量为Y∈{0,1},相当于产品生产过程中,合格与不合格,监控问题可以转化成机器学习中的二分类问题。针对数据集X和Y,预测函数会根据输入特征X来计算输出值h(x)。我们的任务是构造一个hθ函数,来映射数据集中的输入特征X和输出值Y,使得预测函数hθ计算出来的值与真实值Y的整体误差最小。构造hθ的关键就是找到合适的θ和θ0值,即模型参数。

Logistic回归虽然名叫回归,但其实是分类器的一种,可以很好的处理二分类问题。在二值变量的Logistic回归模型中,采用的是对机会比的自然对数(称为“logit”)建模的方法,其公式为

(1)

由于感兴趣的值是概率,Logistic模型可以转换为概率形式的表达,即

上述形式由激励函数Sigmoid转换得到,Sigmoid函数具有良好数学性质,是凸函数,且任意阶可导,Sigmoid函数公式为

(2)

Logistic分类器的实现也可看作将影响分类结果的每个特征乘上相应的权重,再将结果相加代入Sigmoid函数中,从而得到范围在(0,1)的数值。

根据前述提到的预测函数,在Logistic回归模型中,预测函数为

hθ(X)=σ(z)=σ(-θ0-θTX)=

其中:hθ(X)表示在输入值为X,参数为θ0,θT前提下y=1的概率。当hθ(X)≥0.5时y=1,当hθ(X)<0.5时y=0。用概率论的公式写作

hθ(X)=P(y=1|X,θ)。

此时考虑该模型的成本函数。首先,计算单个样本X,Y其预测值与真实值的误差,根据最大似然估计的成本公式[22]如下:

即

Cost(hθ(X),y)=-ylog(hθ(X))-

(1-y)log(1-hθ(X)),

(3)

则很快计算出所有样本的成本函数为

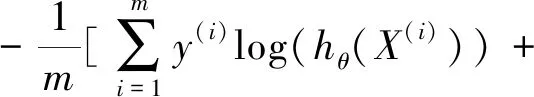
(1-y(i))log(1-hθ(X(i)))]。

(4)

找到模型的成本函数之后,通过梯度下降等优化迭代算法得到参数的最优解[22],从而计算出观测样本的分类概率,分类概率可用于构建控制图。

1.2 Lasso惩罚似然方法

在半个世纪以前,Logistic回归模型常常应用于生物医学研究,目前在数据建模中的应用更为广泛。当m>N时,会出现参数过多的情况,模型会变得不稳定,出现过拟合的情况。在机器学习中为了避免模型的过拟合,会在最小化模型误差的同时对参数进行正则化。考虑多元线性回归问题:

yi=Xiβ+εi,i=1,2,…p

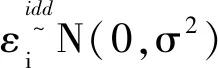
(5)

其中:λj为惩罚参数,也叫做正则化参数[23];gλj是惩罚方程。当gλj(|βj|)=λ|βj|,λ为常数时,相应的惩罚似然方法被称作Lasso[24]。在Lasso方法中,当λ取值越大时,不重要因素的系数随着λ增大而趋近0,当λ足够大时,不重要因素的系数会变成0,此时就实现了系数的稀疏性处理。同时,惩罚似然方法可以通过LARS算法实现高效求解[25]。使用Lasso正则化,也即机器学习里面提到的L1正则化,可以让模型参数向量里元素为0 的尽量多,排除对预测值没有影响的特征,在模型计算时减少特征数量,当控制图出现报警的时候,结合Lasso的特征选择,可以更方便的对偏移因素进行诊断。同时也提高了模型的可解释性。

1.3 Real-time contrasts 实时对比

统计过程控制通常可以分为2个不同的阶段。在阶段1,我们试着去建立一个生产过程并使之运行稳定,从稳定运行的过程中收集一组过程数据代表受控数据集;阶段2则通过阶段1的受控数据集建立控制图,并监控接下来的生产过程,当异常出现时给出警报并诊断异常因素。阶段1的数据S0往往用来估计受控过程的数据分布f0(x)。为了进行数据的实时对比监控,当前的观测数据会拿来与阶段1数据S0进行对比分析,因为在每个时刻点观测到的数据样本都是有限的,所以采用移动窗口来将当前观测数据和部分过去时刻观测数据进行结合,以此与参考数据集S0进行对比。在移动窗口内的数据被记作Sw(t),包含了最近的Nw个观测值Sw(t)={Xt-Nw+1,…,Xt-1,Xt},作为进行分类的对比数据集。由于一旦获得新的观测数据移动窗口就会被更新,因此移动窗口中的数据会实时与参考数据集进行对比。

对于RTC的方法,将参考数据集和移动窗口数据集分为2组:参考数据集S0标记为0,移动窗口数据集Sw(t)标记为1,即

接下来可以通过合适的分类器对这2类数据进行学习,得到分类错误率、分类概率,或者其他信息,以此判断过程是否受控。例如,有控制图将分类错误率作为监控变量,过程没有偏移的时候,分类错误率会很高;当存在偏移的时候,参考数据和移动窗口数据来自不同分布,分类错误率会较小。有些分类器不仅可以得到分类错误率,还可以直接得到分类概率,分类概率可以用做监控变量。

2 基于惩罚Logistic回归多元控制图

当参考数据量少且分布未知的时候,机器学习的方法比传统控制图更能发挥优势。在机器学习和深度学习的领域中,Logistic回归其实是一种分类模型,且可以将样本属于哪一类的概率计算出来,这种概率有助于我们的决策。监督学习的问题也就是在规则化参数的同时最小化误差,结合Logistic回归的成本函数(4)和对参数的Lasso正则化,此时要计算的模型成本函数为

(1-y(i))log(1-hθ(X(i)))]+λ‖θ‖1=

λ‖θ‖1,

(6)

其中:λ为惩罚力度。

基于Lasso惩罚的Logistic回归模型的成本函数式(6)是凸函数,似然部分可微,因此可以将此问题看作标准的凸优化问题来求解[26]。当通过梯度下降算法解出模型参数的最优值后,则可得到观测样本合格与否的分类概率。

基于惩罚Logistic回归模型构建监控统计量的时候,考虑Logistic模型对分类概率的预测能力,即

为提高控制图敏感性,研究决定采用机会比的自然对数作为监控变量,即

(7)

其中:xj是样本观测向量;参数θ可通过优化算法得出。在阶段2监控的过程中,提前假设观测样本属于分类1,此时计算出式(7)的值,如果较大则代表分类正确,即样本失控;如果较小则表示分类错误,样本受控。因此在移动窗口中,监控统计量为移动窗口内Nw个样本的T的平均值,即

(8)

当T(Sw(k))大于某一值h的时候,称该过程失控,h为接下来要计算的控制限。

3 LR-chart设计

研究对提出的LR-chart进行了设计,计算控制图的控制限。探讨模型中的参数对控制图设计的影响,例如惩罚系数c,移动窗口大小Nw。随后对提出的控制图与现有的D-SVM[20],RTC-RF[18]控制图进行了性能的对比分析,发现研究提出的控制图有着优异性能,在提供样本分类概率信息的同时能进行高维数据下的故障因素识别。

3.1 控制限和ARL(average run length)的计算

研究采用的编码语言是Python,该语言方便操作,针对机器学习有大量的运算包可以使用。由于研究采用的是移动窗口的形式对数据进行处理,然后进行监控,在开始采集观测样本进行监控的时候,起初移动窗口内的观测样本是不足Nw的,如果不加调整直接进行监控,控制图会在移动窗口搜集够了Nw个样本后才开始运行,这样会造成控制图报警的延误。为了避免此问题,首先在除去So的受控数据N中随机抽取Nw-1个样本,与控制图开始时收集到的1个样本进行组合构成第1个移动窗口。随后,当观测数据每增加1个,相应的来自受控数据集的样本就减少1个,以保证移动窗口大小是恒定在Nw的。直到移动窗口内的数据完全来自观测数据,此时可以通过在观测数据中移动窗口来进行控制图的设计,如上述提到的RTC原理。

不同的控制图计算控制限的方法也会不同,在阶段2中,通常是给定ARL0来确定对应控制图的控制限。采用二分法进行控制限的搜索。假定A0为给定的ARL0的值。首先确定好控制限的搜索范围[CLl,CLu],该范围可以通过监控统计量的取值范围来确定。设定搜索精度为e,确定搜索经历M次迭代过程,对于其中的一次迭代,步骤如下:

(1) 给定控制限,令CLm=(CLl+CLu)/2;

(2) 在过程没有发生偏移的情况下运行控制图直到出现报警;

(3) 记录RL0,大量重复过程(2),计算出CLm对应的ARL0;

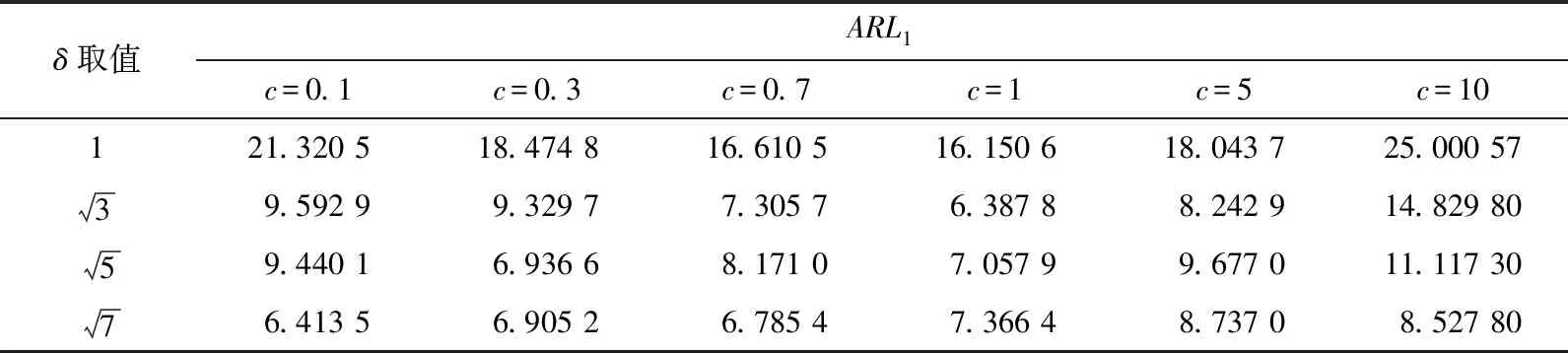
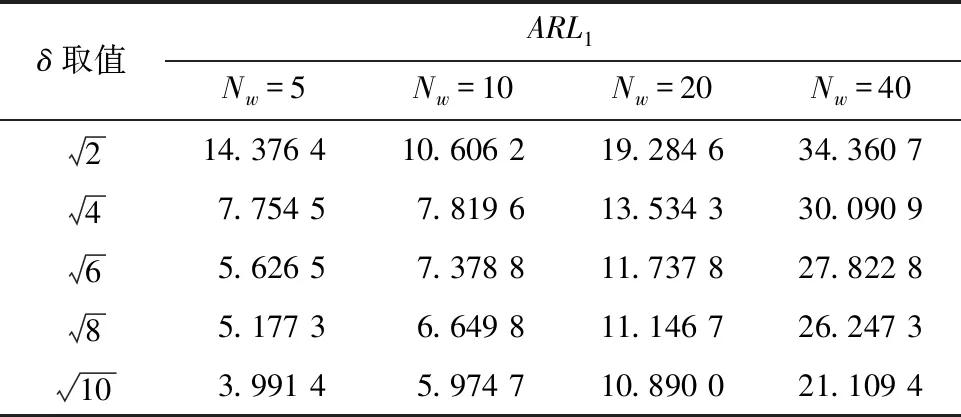
(4) 如果计算得到的ARLo落在[A0-e,A0+e],则停止迭代,此时的CLm为寻找的控制限。如果ARL0>A0+e,令CLu=CLm,继续执行步骤(1)～(3)。如果ARL0

由于给定ARL0,因此不同控制图对异常点的检测性能可通过ARL1值的大小进行比较。ARL1值大表示检测性能较差;ARL1值小表示检测效果更好。

3.2 模型参数选择

由上述模型可知,在分类器进行分类的过程中,Lasso惩罚项对模型结果是有重要的影响。同时,在构建控制图时采用的移动窗口大小Nw对控制图的敏感度也是有影响的。研究讨论如何进行惩罚系数c及移动窗口大小Nw的选择。

首先探讨惩罚系数c对控制图性能的影响。构造维度d=100的正态分布过程,通过该分布生成N=1 000组受控数据,其中随机抽取N0=100作为参考数据集S0,给定移动窗口为Nw=10,且ARL0≈200,通过计算不同惩罚系数及不同偏移程度下ARL1值来衡量参数c对于控制图性能的影响。取d=100维,给出衡量偏移的一种表达为

(9)

表1 控制图取不同c值的ARL1值

图1 不同c值下的ARL1值趋势Fig.1 Trends of ARL1 values with different c values

研究移动窗口大小Nw对于控制图性能的影响,计算d=100,c=1时,不同Nw对应的ARL1的值,结果见表2。由表2可知,在Nw∈[5,15]范围内,对大偏移的检测是没有较大差异的,但是在对小偏移的时候,Nw越小越不敏感。但当移动窗口Nw超出15并增加时,则会降低控制图的对于无论大还是小偏移的敏感性,导致更差的控制图性能。由此可知,在后续实验中,可选取移动窗口Nw=10。

3.3 性能对比

表2 不同移动窗口大小的ARL1值

4 实际案例

将设计好的控制图应用在一个实际案例中,考虑从手机组装过程中收集的相机性能测量数据集。

表3 不同控制图的性能对比

对每个手机,通过屏幕上的5个点来收集相机对焦的数据集。这些位置分布在手机的中心、左上角、右上角、左下角、右下角。收集到的手机相机生产过程的数据集为X=(x1,x2,x3,x4,x5)。我们收集到了来自2 000部手机的正常生产过程的数据集,其中随机抽取1 000个数据作为受控数据集S0来构建控制图,剩下的1 000个数据留作测试数据。该数据的描述性统计部分见表4,该数据的每个xi的分布是不满足正态假设的,且每个xi的分布是类似的,如图2中x1的分布形状。

表4 受控样本的描述性统计

图2 x1的分布直方图Fig.2 Distribution histogram of x1

从受控数据集S0中随机抽取N0=100样本点作为参考数据集,其中窗口大小设定为Nw=10,惩罚参数设定为c=1,给定ARL0≈200时,RTC-LR的控制限为h=0.508。在控制图正常运行了100个样本点的时候,为后续数据添加3个单位的偏移,以此来观察控制图的检出性能。图3展示了RTC-LR图在前200个样本中的表现,在偏移发生第6个样本点的时候给出了警报。

图3 案例数据的控制图显示Fig.3 Control chart display of case data

5 结论

研究提出了基于Lasso惩罚的Logistic回归模型建立的控制图用来监控多元过程,监控统计量是结合了RTC移动窗口的平均对数机会比。在Lasso惩罚的作用下,多元过程的变量得到了提取,重要影响因素的权重为非零,其余为零,方便在控制图报警之后对异常因素进行诊断,达到了阶段2控制图监控和诊断的双重目的。对控制图中的参数进行了调试和选择,随后在与其他控制图对比的过程中,显示出了其优良的性能。最后通过一个手机相机性能评价的实际生产案例来进行控制图的应用。