四维自治超混沌模型及其电路实现

尹社会,王记昌

(河南工业职业技术学院,河南 南阳 473000)

混沌是某些确定性非线性动力学系统中对初始条件极端敏感的运动表现,是一种普遍存在的混乱无序、类随机、难以预测且具有一定规律性的物理现象。混沌作为一种复杂的非线性运动行为,在生物工程、复杂物理和信息学等领域得到了广泛的应用,并且在不断地改变人类对于现实世界的许多传统看法[1]。现在混沌理论系统的研究越来越成熟,对混沌信号的基本特性的研究成果越来越多,这些研究在图像数据加密、信号检测与处理、保密通信、图像数据压缩、高速检索、非线性时间序列的预测、模式识别、电机控制系统、故障诊断等领域有良好的应用前景。当前研究的混沌电路中,如经典Lorenz电路、蔡式电路、Chen电路等的研究都非常成熟,对新构造的混沌系统的研究更多地集中在三维系统中[2-11],一般以非线性项的变化来呈现不同拓扑结构的吸引子,这类系统的电路实现相对简单,但是在工程上许多电路的设计和搭建并不与现有系统完全一致,达不到理想的状态,许多在实际电路搭建中的误差和干扰有很大改进空间。目前高维混沌系统和超混沌系统电路的研究并不多[12-13],与低维混沌系统相比高维混沌系统和超混沌系统的结构更为复杂,有多个系统变量以及多个系统参数,这些都可以用来作为密码系统的各种子密钥,算法的密钥空间大大高于低维混沌方程构造的密码系统,系统变量的时间序列相对于低维系统更加无规律,不可预测,更适系统合于加密。因此,研究高维混沌系统和超混沌系统具有重要的理论和实际应用价值。另外,现有低维混沌系统一般存在系统各个通道电路结构比较复杂、不易于系统电路的维数扩展和硬件实现、保密性较差等问题,这些也是目前关于混沌电路搭建过程中的关键问题。

我们研究一个新超混沌模型的动力学行为等问题,并根据Multisim搭建了模块化模拟电路,该电路结构简单、便于集成,对混沌系统在保密通信和信息处理等领域中的发展具有促进作用。

1 新混沌模型的基本分析

张转周等[14]提出了一个三维非线性混沌系统,其数学模型为

(1)

研究基于该三维非线性模型构建了一个新四维超混沌模型,通过在第1个方程中加入扰动项,并引入第4个方程。为了参数设置的方便考虑,在新系统中部分参数进行了整合考虑,其数学形式为

(2)

其中:a、b、c、e均与系统(1)的参数相似,但是需满足条件a>0,b>0,c>0,e>0。

1.1 Lyapunov指数和Lyapunov维数

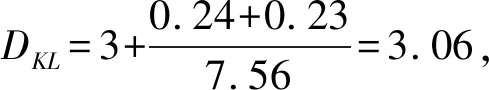
图1 系统(2)轨线的相图Fig.1 Phase diagram of system (2) trajectory

1.2 平衡点及其稳定性

通过计算可得系统(2)具有唯一非原点的平衡点S(0,0,20,0),根据局部线性化方法,容易得到相应的特征值为λ1=-1,λ2=-13.349 4,λ3=0.343 9,λ4=6.905 5。根据Routh-Hurwitz 条件,系统平衡点对应的特征方程具有正的和负的特征值,可知此平衡点为一个不稳定的指标2鞍点。

1.3 吸引子的存在性和耗散性

由于微分方程组的向量场f(X)的散度为

(3)

(4)

即体积元V0在t时刻收缩为体积元V0e-(a+c+1.1)t。事实上,系统的轨迹最终渐近地运动到一个特定的零体积的极限集中,即一个吸引子上。

1.4 系统参数变化的影响

系统参数的变化对于系统(2)的影响决定着系统(2)的动力学行为的变化。 因此通过Lyapunov指数谱图和分岔图的研究能够更清楚的认识系统的动力学变化特性,如图2所示。系统(2)在固定其他参数的情况下研究参数e的变化对系统动力学行为的影响的Lyapunov指数谱图,可以看出在区间[-10,-3.3]内,系统处于稳定平衡状态,但其中出现一个尖峰使得最大Lyapunov指数接近0或大于0,即存在周期轨或短暂混沌现象;在区间[-3.3,5.6]内,有一个Lyapunov指数为正,说明系统处于混沌状态,但其中也存在向下尖峰,即在e=-3附近出现Lyapunov指数全为负的情况,会出现稳定到平衡点的现象;在区间[5.6,50]内,有2个Lyapunov指数为正,说明系统处于超混沌状态。进一步通过吸引子相图进行判断,我们发现这些尖峰的存在与初值的选择有关,即在开始的一段时间内运动轨线并没有稳定在吸引域内,所以出现Lyapunov指数的剧烈变化,如图3所示。当参数e=-3时系统吸引子相图可以明显看出,运动会在很短一段时间内聚集到一个平衡点(图3中用五角星标记)附近。此时系统已经具有3个平衡点,分别为S(0,0,20,0),S±(±5.57,±3.48,0.625,±3.48)。系统(2)对参数e的变化分岔图如图4所示,结论与Lyapunov指数谱图所得结论具有一致性。

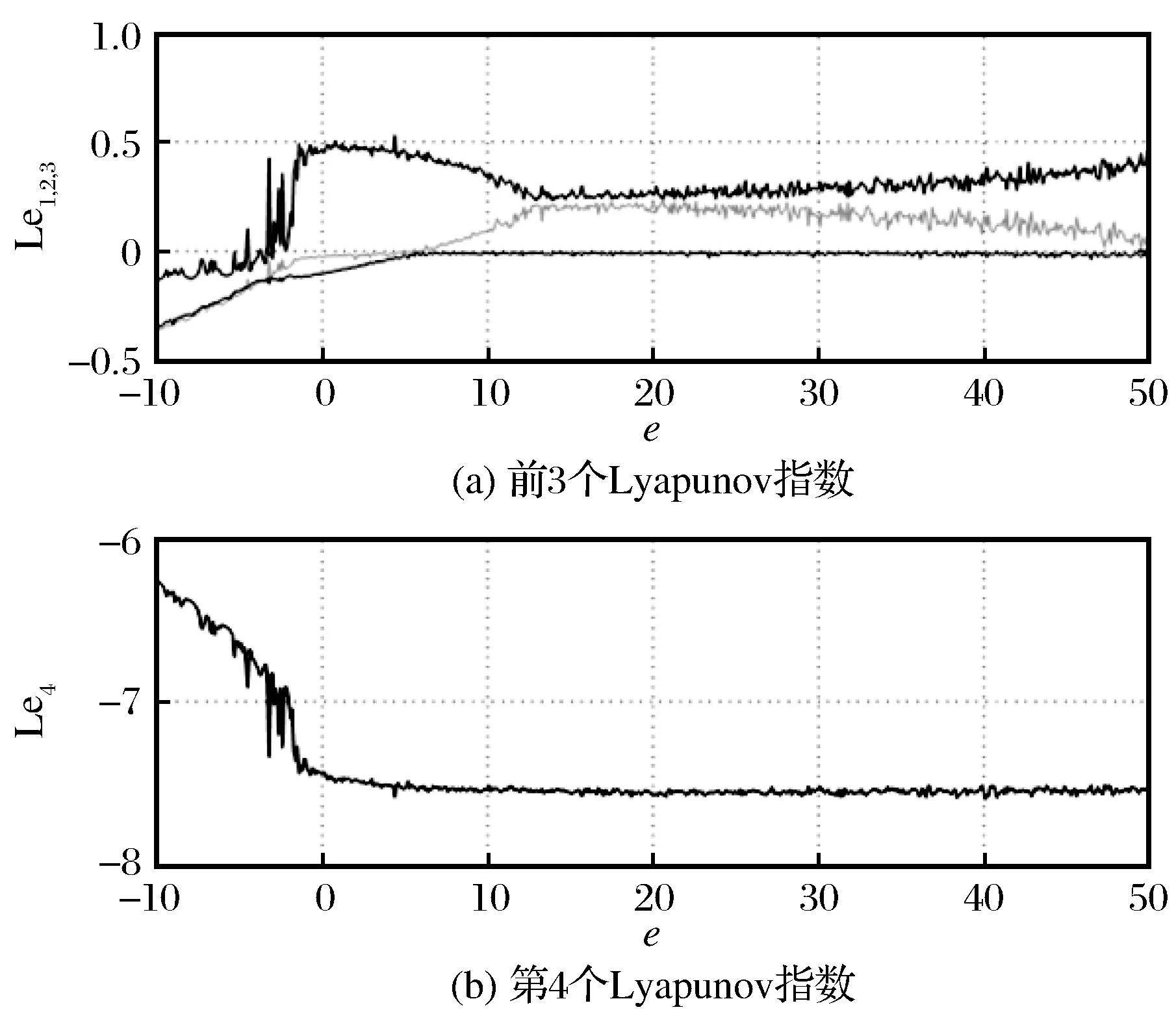
图2 系统(2)的Lyapunov指数谱图Fig.2 Lyapunov index spectrum of system (2)

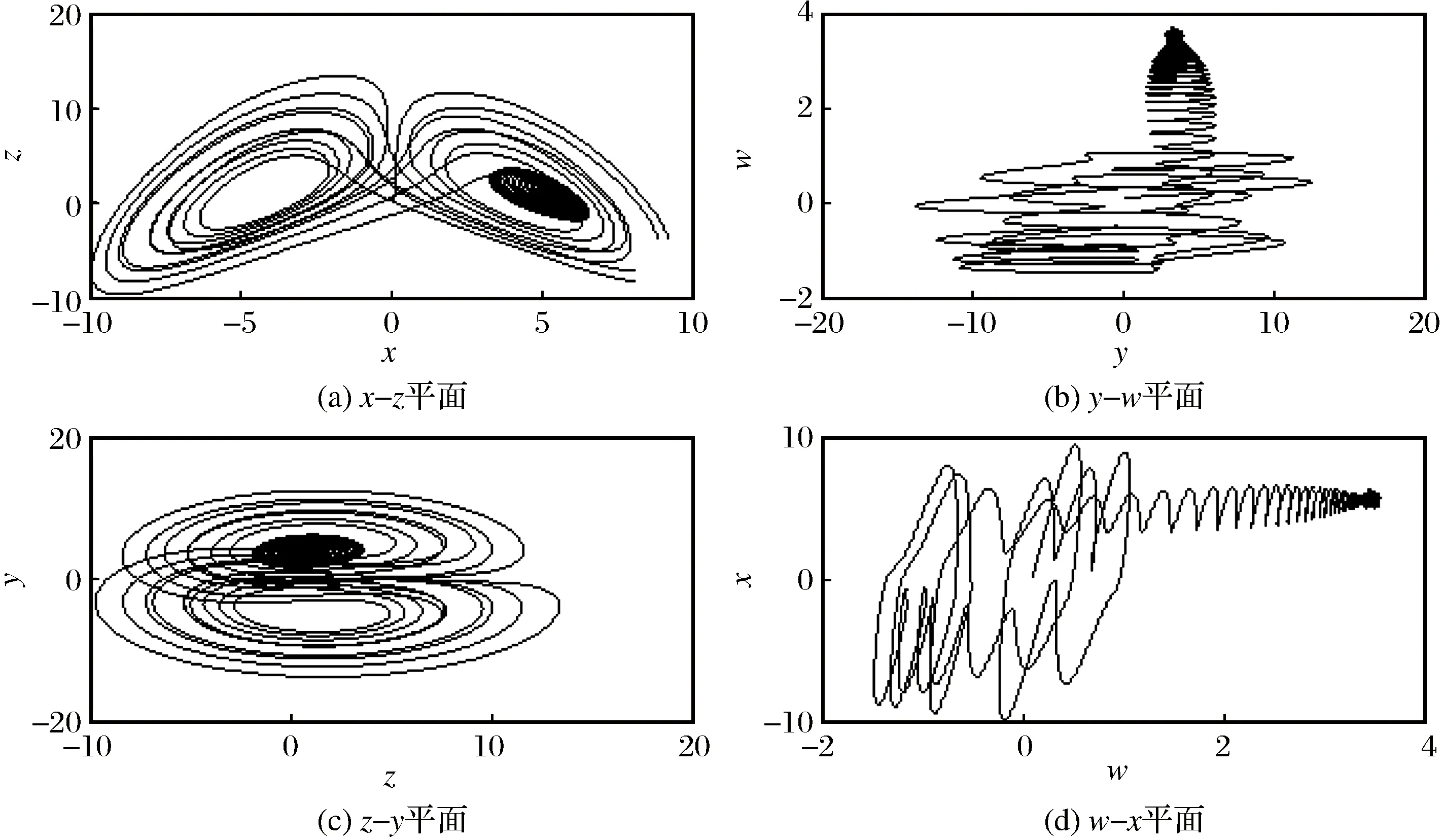
图3 e=-3时的相图Fig.3 Phase diagram when e=-3

2 系统(2)模块化电路搭建

根据模块化搭建电路的原则,采用线性电阻、线性电容、运算放大器、模拟乘法器、直流电源等来设计系统(2)的电路。运算放大器实现加减和积分运算,模拟乘法器实现非线性项乘积运算。实验时将混沌信号的输出电平调小为适合运算放大器进行线性运算的范围,因为系统变量的变化不影响系统的状态与性能,因而并不影响结论。

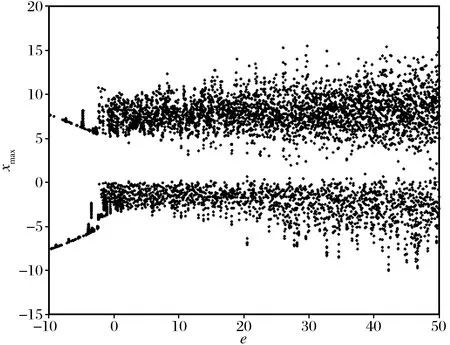
图4 系统(2)的分岔图Fig.4 Bifurcation diagram of system (2)

模拟电路原理如图5所示,由于图5中已经标注了各个元件对应的取值,这里不再重复说明。电路实现吸引子相图如图6所示,和理论计算效果非常接近,数值仿真平面相图如图7所示,说明新超混沌模型具有物理可实现性,为进一步的应用提供了可靠的保障。

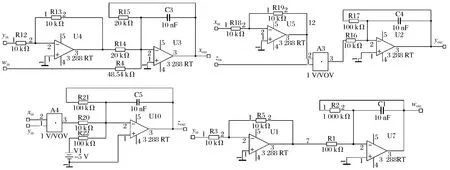
图5 电路原理Fig.5 Schematic circuit diagram

图6 电路实现吸引子相图(单位:V/div)Fig.6 Circuit implementation attractor phase diagram (unit:V/div)

图7 吸引子平面相图Fig.7 Attractor plane phase diagram

3 结论

研究提出了一个新超混沌模型,系统含有5个参数,状态方程中只含有2个非线性乘积项和1个常数项,其余均为线性项,结构简单但动力学行为丰富。通过理论分析、数值仿真、Lyapunov指数谱、分岔图和Poincare截面图分析了新系统的基本动力学特征,验证了系统丰富的混沌特性。该超混沌模型参数较多,系统处于混沌状态的参数变化范围较大,而且可以电路实现。因此,上述研究结果可为该新超混沌系统的工程应用以及进一步的定性行为分析和定量分析等提供理论依据,在电子测量、图像加密以及保密通信等领域具有潜在的应用价值。