Acceleration tracking control for a spinning glide guided projectile with multiple disturbances
2020-02-24QiCHENXugngWANGJingYANGZhongyunWANG
Qi CHEN, Xugng WANG, Jing YANG, Zhongyun WANG
a School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China
b No. 203 Research Institute of China Ordnance Industries, Xi’an 710065, China
KEYWORDS Spinning glide guided projectile;Cross-coupling;Acceleration tracking;Nonlinear control;Extended state observer
Abstract A novel acceleration tracking controller is proposed in this paper, for a Spinning Glide Guided Projectile(SGGP)subject to cross-coupling dynamics,external disturbances,and parametric uncertainties. The cross-coupled dynamics for the SGGP are formulated with mismatched and matched uncertainties,and then divided into acceleration and angular rate subsystems via the hierarchical principle. By exploiting the structural property of the SGGP, model-assisted Extended State Observers(ESOs)are designed to estimate online the lumped disturbances in the acceleration and angular rate dynamics. To achieve a rapid response and a strong robustness, integral sliding mode control laws and sigmoid-function-based tracking differentiators are integrated into the ESO-based Trajectory Linearization Control (TLC) framework. It is proven that the acceleration tracking controller can guarantee the ultimate boundedness of the signals in the closed-loop system and make the tracking errors arbitrarily small. The superiority and effectiveness of the proposed control scheme in its decoupling ability, accurate acceleration tracking performance and antidisturbance capability are validated through comparisons and extensive simulations.
1. Introduction
With the advancements in sophisticated sensors, information processing platforms,and actuating devices,guided munitions have received considerable attentions from the research community due to their prominent characteristics of range extension, quick responses, precision strikes, and low costs. The Spinning Glide Guided Projectile (SGGP) is a kind of gunlaunched fin-stabilized guided munitions equipped with a booster rocket,two pairs of canards,and a Guidance,Navigation, and Control (GNC) system.1-7The SGGP is launched from a gun providing its initial kinetic energy and deploys a set of tail fins to maintain stability after exiting the gun barrel.A short time after the initial launch, a solid-propellant rocket motor ignites and works for a few seconds to provide additional boost. Once the SGGP reaches the apogee, its canards are deployed, and the GNC system uses the steering canards to glide the projectile to its target. To fulfill the precise strike mission, an advanced flight controller is essential for the glide trajectory.During the entire flight,the SGGP spins around its axis of symmetry and is not controlled in the roll channel.This property is beneficial to simplifying the structure of the control system, eliminating the projectile’s asymmetry, and relaxing the manufacturing error tolerance. However, the spinning of the guided projectile also induces strong cross-coupling between the pitch and yaw channels, which complicates the controller design. In addition, variations in the aerodynamic parameters associated with unmodeled uncertainties and external unknown disturbances always exist in the SGGP system, which further make the development of a high-performance flight controller with some robustness a significant challenge.
In recent years, various control methods have been investigated for the flight controller design of SGGPs in the literature. In Ref.8, a guidance and control strategy with reduced sensor and actuator needs was introduced to enable precision and trajectory shaping for a guided projectile. However, the flight controller used in this work is somewhat empirical and does not consider the coupling effects. In Ref.9, a flight controller was designed for guided projectiles via a nonlinear dynamic inversion method and a timescale separation scheme.However,the controller introduced in this work does not consider the disturbances. To enhance the control performance subject to spinning, two-loop and three-loop lateral acceleration autopilots that elaborately take into account of the projectile’s spinning were introduced in Refs.10-13based on the philosophy of a PID regulator. These linearized approaches work well under nominal conditions but suffer from the drawback of performance degradation when the guided projectile distinctly deviates away from its designed trim point or conducts aggressive maneuvers. Moreover, uncertainties caused by model simplification and external disturbances are not considered in these studies. Yan et al.14analytically studied the stability of coning motion for spinning missiles with a PD attitude autopilot and found that stable region of the design parameters for the attitude autopilot shrinks so significantly due to the spinning of the missile that it is impossible to ensure the stability of an autopilot by means of the conventional method. To overcome the limitations of the previous approaches, nonlinear control schemes are investigated to achieve a good control performance for autopilot design. By adopting Loop Transfer Recovery (LTR) together with gain scheduling approach, robust autopilot design was proposed in Ref.15for surface-to-air missiles. In Ref.16, a fixed-time adaptive model reference sliding mode controller was proposed for missiles with large speed ranges, in which mismatched disturbances and un-modeled dynamics were taken into account. Based on the dynamic neural network and the single network adaptive critic method, a model-free adaptive optimal trajectory tracking controller was designed for a solid-rocket-powered vehicle in Ref.17. A novel envelopeconstraint-based neural controller was proposed in Ref.18for hypersonic vehicles with unknown non-affine formulations.In Ref.19, a robust control scheme was proposed for flexible vehicles with actuator dynamics based on nonlinear disturbance observer and Nussbaum function technique. However these studies did not consider the cross-coupling effects. In the work of Yan et al.,20the dynamic inversion theory was used to construct a controller for a spinning missile with nonlinear coupling characteristics, where the subsystem was designed separately according to the cascade structure method.It is worth noting that this method greatly depends on the modelling accuracy of the spinning missile. In the work of Li et al.,21a three-loop autopilot was designed for a spinning missile by using the state feedback and eigenvalue placement.This approach brings cross-feedback compensation and achieves control decoupling between pitch and yaw channels.However,the above studies did not consider the uncertainties or disturbances.
Recently,Trajectory Linearization Control(TLC)has been proven to possess remarkable performance in handling nonlinear tracking control and disturbance rejection problems. It combines an open-loop nonlinear dynamic inversion and a linear time-varying feedback stabilization in a novel way,providing robust stability and performance. Therefore, various TLC and modified TLC strategies have been widely used in the nonlinear flight controller design. In Ref.22, on the basis of the TLC technique, an ascent flight controller was designed for an X-33 reusable launch vehicle.In Ref.23,the TLC technique was employed to design the adaptive course control algorithm for an unmanned surface vehicle with un-modeled dynamics and input saturation. However, as proven by the theoretical analysis established in Ref.24, TLC only achieves local exponential stability and thus cannot ensure robustness against large uncertainties.To improve the robustness of TLC against large uncertainties, various modified TLC techniques have been reported.By integrating a neural network into the framework of TLC, an enhanced TLC method was proposed in Ref.25,in which the neural network is used to directly compensate for the uncertainties,and thus,the controller performance can be effectively improved.Further extensions to the adaptive neural-network-based control are presented in Refs.26,27. A disturbance observer-based control framework leads to another kind of approach for improving TLC performance.A compound control scheme combined with TLC and Linear Extended State Observers (LESO) was investigated in Ref.28for hypersonic reentry vehicle attitude tracking system.Therein, LESO are constructed to estimate the uncertainties in each loop, and the tracking performance of the controller is enhanced. Similarly, Extended Disturbance Observers(EDO) and Finite-time Model-assisted ESO (FMESO) were implemented in Refs.29,30to estimate lumped uncertainties,by which satisfactory attitude tracking performance can be guaranteed by TLC in the presence of uncertainties. A Nonlinear-Disturbance-Observer-Based Control (NDOBC)method was presented in Ref.31for the longitudinal dynamics of a generic airbreathing hypersonic vehicle under mismatched disturbances. In Ref.32, a DO-based reliable H∞fuzzy controller was developed for the attitude tracking control problem of entry vehicles. To ensure a fast convergence and precise tracking performance, a novel disturbance-observer-based gain adaptation high-order sliding mode control method was proposed for trajectory tracking of hypersonic vehicles with complex unknowns in Ref.33, where the complicated unknowns, including external disturbances and system uncertainties, are merged together into a single term that is estimated by a Disturbance Observer (DO). By adopting the Nussbaum Disturbance Observer(NDO)and the dynamic surface control technique,a nonlinear attitude controller was proposed in Ref.34for near-space vehicles in the presence of disturbances and input saturation. In Ref.35, a sliding mode control based approach which ensures the finite time convergence of the vehicle to the desired signals was presented for the autopilot design.
However,the aforementioned control approaches only deal with the cases for which the roll channel of the vehicle is stabilized,ignoring the cross-coupling effect that arises between the pitch and yaw dynamics. Due to the cross-coupling effect, the maneuver in the pitch or yaw channels will generate an extra response in the other channel. In order to guarantee the good control performance, it is necessary to deal with the pitch and yaw channels coordinately in the autopilot design.In these circumstances,traditional separated channel design methodology may degrade the performance of autopilot. Moreover, in contrast to hypersonic vehicles or missiles, considering the gunlaunched environment, the control authority provided by SGGP is limited due to small onboard electronic suites and control mechanisms,which makes SGGP more sensitive to disturbances.While the cross-coupling will further complicate the effect of disturbances on the SGGP dynamics. These factors make the design of a high-performance flight controller for SGGP a significant challenge. Due to the distinct nature of the SGGP, there is a very limited number of studies reporting the results of exploiting the autopilot design via TLC for SGGPs. Moreover, in Refs.26-30, the angle of attack and the angle of sideslip are assumed to be measurable directly. However,this assumption cannot be satisfied for SGGPs due to the limitations of onboard electronic suites. These practical issues restrict the application of existing nonlinear approaches in the autopilot design for SGGPs. Consequently, how to design an acceleration tracking controller for SGGPs is an imperious demand. Motivated by the above observations, this paper investigates a novel acceleration tracking controller for an SGGP that is subject to cross-coupling dynamics,external disturbances, and parametric uncertainties. The stability of the proposed controller is analytically analyzed,and its superiority over other controllers is demonstrated via extensive simulations. The main contributions of this paper are as follows:(A) A novel nonlinear model of the SGGP for acceleration tracking problem is established, where the cross-coupling effect between the pitch and yaw dynamics is elaborately taken into account, and the assumption that the angle of attack and the angle of sideslip are measurable is totally removed. (B) By exploiting the structural property of the SGGP, a model information-assisted ESO is constructed to estimate the lumped disturbance with reduced observer bandwidth, even without knowing the exact form of uncertainties. (C) By integrating the Integral Sliding Mode Control(ISMC)and the Sigmoid Tracking Differentiator (STD) into the ESO-based Trajectory Linearization Control (TLC) framework, the cross-coupling effect and lumped disturbances can be precisely compensated for, thus rapid acceleration response and good anti-disturbance ability are obtained.
This paper is organized as follows. The cross-coupled dynamic model of the SGGP is derived in Section 2.The nonlinear acceleration tracking controller design is given in Section 3. In Section 4, the stability analysis of the closed-loop system is presented. Section 5 presents the numerical simulation results and detailed comparisons with other controllers.Conclusions are given in Section 6.
2. Cross-coupled dynamic model of spinning glide guided projectile
The spinning of an SGGP induces cross-coupling between the pitch and the yaw. It is rational to suppose that the spinning rate remains constant over a short interval in the flight.11Therefore, the dynamics in the rolling channel can be eliminated for the acceleration control design. Drawing on Ref.11,the mathematical dynamics of an SGGP in the pitch and yaw channels are given by


Fig. 2 Rotation from velocity vector to body axis.


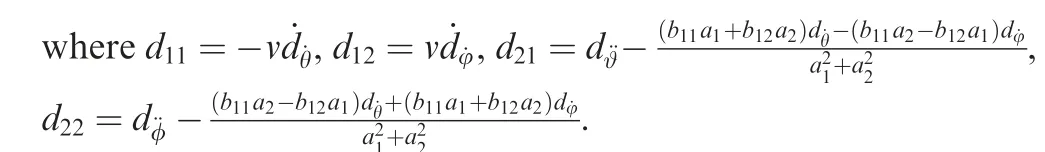
The main feature of system (10) is that the pitch and yaw dynamics are severely coupled with each other. The crosscoupling between the normal and lateral acceleration dynamics is induced by the parameter a2that depends on the Magnus force coefficient and the body spin rate, while the crosscoupling between the rotational dynamics is induced by the Magnus force and moment coefficients, the static moment coefficient, the body spin rate as well as the canard deflection angles in the body-fixed coordinate system.
For simplicity, we define

Then, we can rewrite Eq. (10) in the following nonlinear cascaded form

3. Nonlinear control law design for an SGGP with disturbances


3.1. Nonlinear control for acceleration loop

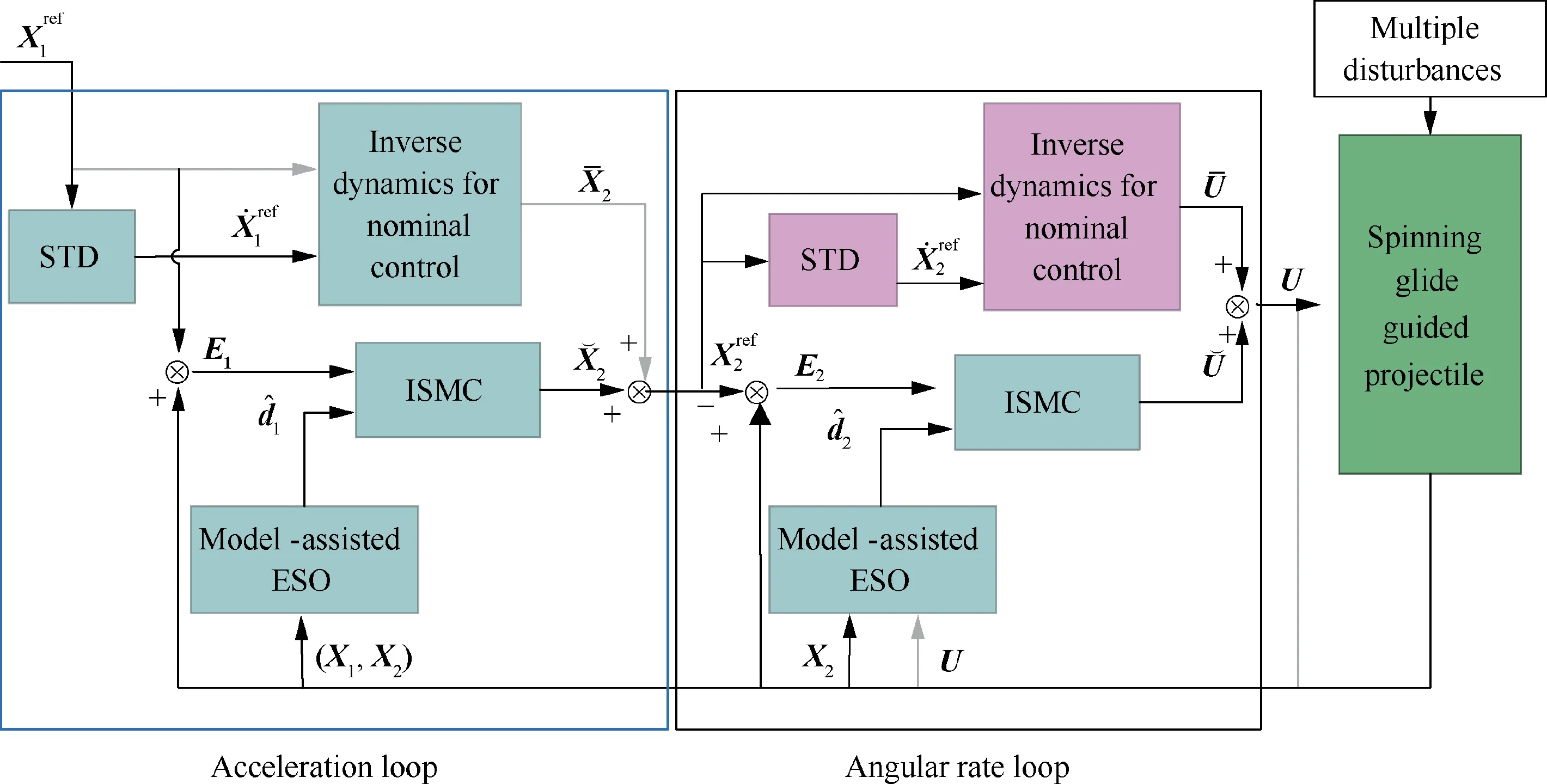
Fig. 3 Structure of proposed control scheme for SGGP.


Using Eq.(16)and the reaching law(18),differentiating the sliding surface (17) with respect to time yields

Then,the model-assisted ESO for system(21)is formulated as

3.2. Nonlinear control for angular rate loop



4. Stability analysis
In this section, the ESO stability and the closed-loop stability of systems (11) and (12) under the proposed model-assisted ESO- and -ISMC-based TLC acceleration tracking controller are established.

Before establishing the ESO stability analysis, it is necessary to introduce the following assumption that has been widely utilized in the proof of observer stability.
Assumption 3.
The functions F1,F2belong40,41to C2and are globally Lipschitz with respect to X1, X2, X3, i.e., there exists a set of known positive constants c1, c2such that
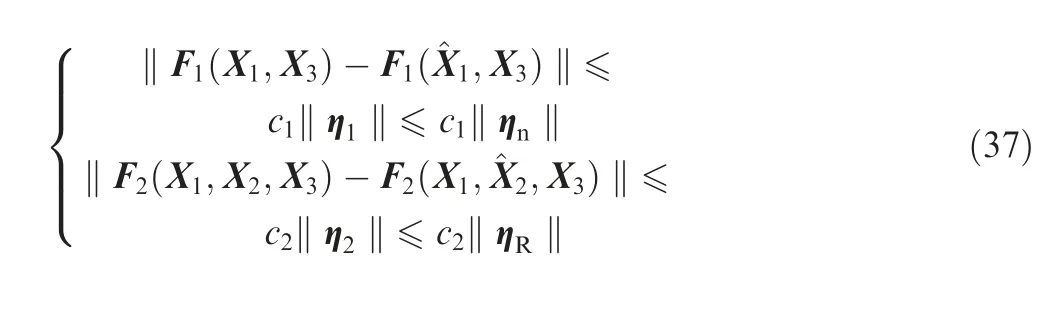
Theorem 1. Considering the estimation error dynamics of the acceleration loop depicted in Eq. (36), there exists a definite matrix P satisfying GTP+PG=-I for the Hurwitz matrix G defined with the results of Assumption 3; if the observer bandwidth is selected such that ζ≜ω01-2c1ρ1>0 with ρ1=‖Ph1‖,then the designed ESO is stable and the estimation error of the acceleration loop is ultimately bounded and can approach the origin asymptotically.
Proof. Consider the following Lyapunov function candidate

It can be concluded from Theorem 1 that with a sufficiently large value of observer bandwidth, the designed ESO is stable and the upper bound of the estimation error monotonously decreases with the observer bandwidth. Thus, the acceleration state ^X1and the disturbance estimate ^d1can reach their real states with arbitrarily small errors.Although a larger observer bandwidth leads to a better estimation ability,it may also deteriorate the performance robustness of ESO and even cause high-frequency oscillations. Therefore, an appropriate compromise should be made between the estimation quality and the robustness of ESO in practice. Because there is no difference between the estimation error dynamics for the acceleration and angular rate loops, the results in Theorem 1 can be directly applied for the angular rate loop.
Theorem 2. Consider the SGGP dynamics described by Eqs.(11) and (12), the proposed reference acceleration tracking controller, including the virtual controller (24) and the applied controller(35),together with the model-assisted ESO dynamics Eqs. (22) and (33), can guarantee the ultimate boundedness of all signals in the closed-loop system and make the tracking errors arbitrarily small provided that the parameter matrix Λ defined in the following is positive definite:

Proof:. Consider the following Lyapunov function candidate

where,

Inequality (46) means that V(t) is eventually restricted by ς/a. Thus, the ultimate boundedness of all signals in the closed-loop system can be guaranteed.In addition,by increasing the values of control parameters and observer bandwidths,the ultimate upper bound for tracking errors can be made arbitrarily small. This completes the proof.
5. Simulation results and comparison
In this section, numerical simulations and comparisons are presented to demonstrate the performance of the acceleration tracking controller developed in Section 3. The parameters and initial states of the SGGP are given in Table 1.In the following simulations, the canard deflection angles are bounded as-15°≤σic≤15°(i=1,2),and the coefficients of the aerodynamic forces and moments described in Eq.(1)are all varied by -40% of their respective nominal values. In addition, the time-varying unknown disturbances are chosen as [0.2cos(4 t)cos(t)+0.1sin(0.8 t)cos(t), 0.15cos(2 t)cos(t)]Tfor the acceleration dynamic subsystem and as [4cos(3 t)cos2(0.5 t),3cos(t)cos(2 t)+sin(0.5 t)]Tfor the angular rate dynamic subsystem. The main reasons why we choose such form of timevarying disturbances are as follows: (A) we try to approximately model the aerodynamic fluctuations induced by the spinning of the projectile, the harmonic signals can somewhat qualitatively capture the characteristics of aerodynamic fluctuations of SGGP due to the spinning and can be used to evaluate the estimation ability of the designed observers under fast time-varying disturbance with different frequencies. (B) The comparative robustness performance of the considered controllers can also be testified under the bounded disturbances.
5.1. Performance of proposed method
In the proposed method, the design parameters for the STD are chosen to be h=0.02, a=12, b=2, R=1. The bandwidth of ESO for the acceleration loop and angular rate loop are ω01=25 rad/s, ω02=35 rad/s, respectively. The parameters of the controller are mainly tuned based on the results of Theorem 2, which leads to the following values: σ1=5I2,σ2=3I2, ε1=3I2, ε2=1.5I2, λ1=λ2=0.1, and κ1=κ2=0.1. To alleviate chattering, the discontinuous function sgmf(s) is replaced with the sigmoid function

where τ is the width of the boundary layer of the sigmoid function and is set to 0.05.
Simulation results,including the acceleration responses,the angular rates, the deflection angles, the sliding surfaces, and the disturbance estimates, are presented in Figs. 4-8. It is clearly seen from Fig. 4 that the normal and lateral accelerations of the SGGP can track their pregiven reference signals tightly in the absence of uncertainties. Although the normal acceleration signal is highly maneuvered, the acceleration response still tracks its reference with a fast convergence (the setting time is less than 1.5 s)and no overshoot.For the lateral acceleration, a faster tracking performance with a setting time less than 1.0 s can be clearly observed. In addition, the crosscoupling caused by the spinning is effectively rejected by the proposed controller. In the angular rate loop, although the angular rate command changes very quickly, the controller can track the reference signal precisely and rapidly as depicted in Fig.5.Note that there exists an evident margin between the initial reference normal acceleration(0)and the initial condition,which is set as zero,of the differentiator of Eq.(14).In this case, the conventional SOLD will produce the so-called peaking phenomenon which will be shown later. However,because the STD is used to construct the derivative of the reference signal in the proposed control framework, no peakingphenomenon is observed in the pitch plane as illustrated in Fig.5(a).In addition,based on the results of Theorem 2,with finite time convergence, the tracking errors can be suppressed to a much smaller neighborhood of origin by approximately choosing designed parameters of the proposed controller.

Table 1 Parameters and initial states of SGGP.
The time histories of the canard deflection angles both in the nonspinning coordinate system and in the body-fixed coordinate system are shown in Fig. 6. In this figure, σ1cand σ2crepresent the canard deflection angles in the body-fixed coordinate system, while σ1and σ2represent the canard deflection angles in the nonspinning coordinate system. Due to the spinning of the SGGP,σ1cand σ2cvary coordinately with the rolling angle γ, such that the SGGP can generate the corresponding accelerations in the pitch and yaw planes. σ1and σ2can be regarded as the equivalent canard deflection angles in the pitch and yaw planes respectively. It is clearly observed that the deflection angles are well within the saturation limitation as 15°and change smoothly without chattering even though multiple disturbances exist.Fig.7 depicts the time histories of the sliding mode surfaces for the acceleration loop and the angular rate loop.It can be seen that the sliding mode is stable in spite of the cross-coupling and unknown disturbances. Moreover, the sliding surface can be driven into a small neighborhood of origin within a finite time, which is identical to the inherent finite convergence property of the proposed controller, as proven in Section 4. In addition, the convergence rate of the sliding surface in the angular rate loop is faster than that in the acceleration loop. Fig. 8 demonstrates the estimate performance of the model-assisted ESO for a lumped disturbance in each loop. It is observed that the model-assisted ESO estimates the external disturbances and parameter perturbations with a fast speed and a high accuracy.The ability of the ESO to obtain an accurate estimation of the uncertainties in the dynamics contributes to a better disturbance rejection performance as well as a smooth control deflection profile.

Fig. 4 Acceleration tracking performance of proposed method.

Fig. 5 Angular rate tracking performance of proposed method.

Fig. 6 Deflection angles of proposed method.
The acceleration tracking simulations for the SGGP with multiple disturbances and measurement noises are carried out to further demonstrate the performance of the proposed method. In the following simulations, the Gaussian white noises with a standard deviation of 0.07 g are added to the acceleration measurement channel at t=10 s, while in the angular rate measurement channel, the standard deviation of the Gaussian white noises are 0.017 rad/s. The corresponding simulation results are illustrated in Figs. 9-12. In Fig. 9, the effect of measurement noise is clearly observed in the tracking signals,and one can observe that the normal and lateral accelerations have tracked the reference quite accurately in spite of multiple disturbances and measurement noises. It can also be noted that the effect of measurement noise is visible in the sliding surfaces and in the deflection angles, as shown in Figs. 10 and 11. The sliding surface can be driven to a small neighborhood of the origin under the proposed method even in the presence of measurement noises, and it thus provides satisfactory tracking performance. In addition, the control inputs are still well within the saturation constraints. In Fig. 12, an acceptable estimate of the uncertainties can be ensured by the designed observers. Based on the above analysis, the proposed controller has offered satisfactory tracking performance in spite of noisy measurements.

Fig. 7 Time histories of sliding surface.

Fig. 8 Estimates of lumped disturbances.
To further assess the tracking performance of the designed controller with measurement bias errors. Besides the measurement noises, an acceleration sensor bias error with a constant amplitude being 1.5 m/s2and an angular rate sensor bias error with a constant amplitude being 0.02 rad/s are considered at t=13 s. The simulation results are illustrated in Fig. 13. As can be seen,with only measurement noises,the normal and lateral accelerations can track the reference quite accurately in spite of multiple disturbances. While when the measurement bias errors are considered, the performance of the controller will degrade since the tracking error and overshoot are observed in Fig. 13. In practical applications, it is necessary to reduce the measurement bias errors as much as possible for a better control performance.
5.2. Comparisons with other methods
To evaluate the superiority of the proposed controller over classical controllers for the SGGP acceleration tracking problem, the traditional TLC scheme proposed in Ref.22and the Two-Loop PI Regulator Autopilot (TLPIRA) developed in the work of Li et al.11are given for comparison. In addition,to further evaluate the effectiveness of the model-assisted ESO used in both the acceleration loop and the angular rate loop,an ISMC-based controller without observers is also given for comparison.Here,the ISMC-based controller is treated as a reduced variant of our proposed controller. To be specific,the difference between the ISMC-based controller and the proposed controller is that the former one does not contain observers. The main reason that we introduce the ISMC-based controller for comparison is to demonstrate the merits of utilizing model-based observers in the controller development.To make the comparison fair, the controller parameters are selected to be the same as those of our proposed controller.In the conventional TLC, the bandwidth of the pseudo differentiator is wdiff=20 rad/s,and the gains of the feedback controller for the acceleration loop and the angular rate loop are K1=5I2, K2=10I2, respectively. In the TLPIRA, the controller parameters are selected as kp=0.3, kI=0.45,kω=0.75,and kα=1.0.More details on the controller structure and parameter selection can be found in Ref.11.

Fig. 9 Tracking performance of the proposed method with measurement noises.

Fig. 10 Time histories of sliding surface with measurement noises.

Fig. 11 Canard deflection angles of the proposed method with measurement noises.

Fig. 12 Estimates of lumped disturbances.

Fig. 13 Tracking performance with measurement noises and bias errors.

Fig. 14 Acceleration tracking performance of TLC.
The time histories of the acceleration response and angular rate of TLC are shown in Figs. 14 and 15. It can be observed from Fig. 14 that the tracking performance of TLC deteriorates remarkably in the presence of large uncertainties compared with the proposed controller. In particular, the time response of normal acceleration shows severe oscillations for an aggressive maneuvering reference signal. For the lateral channel,even the maneuvering of the pregiven reference signal is mild, the TLC controller still cannot achieve a satisfactory tracking performance, where the lateral acceleration response exhibits evident oscillations as illustrated in Fig. 14(b). Therefore, compared with the proposed controller, the TLC controller is unable to reject large uncertainties. From Fig. 15, it can be seen that the TLC controller only tracks its reference signal roughly, and again, oscillations can be observed in the corresponding time response.Thus,a satisfactory tracking performance in the angular rate loop cannot be guaranteed by the TLC controller.Moreover,a dramatic peaking phenomenon is obviously observed in the initial portion of the pitch angular rate response, which can be viewed as the consequence of the utilization of the SOLD in the TLC structure. This phenomenon occurs because the high gains are used in the SOLD,so the behavior of the derivative signal will shoot up to a large value during the transient phase.By contrast,due to the introduction of the STD,the peaking phenomenon has been totally avoided in the proposed controller as depicted in Fig. 5. This merit can be attributed to the best properties of linear and nonlinear components are all incorporated into the sigmoid function.

Fig. 15 Angular rate tracking performance of TLC.

Fig. 16 Acceleration tracking performance of TLPIRA.
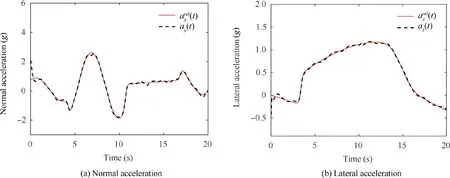
Fig. 17 Acceleration tracking performance of ISMC.

Fig. 18 Angular rate tracking performance of ISMC.

Fig. 19 Comparisons of tracking errors for different methods.
The acceleration tracking performance using TLPIRA is shown in Fig. 16, from which it can be clearly observed that TLPIRA cannot achieve accurate tracking of normal/lateral acceleration signals under lumped disturbances because obvious tracking errors around the steady-state response are detected. Moreover, dramatic changes and large oscillations in the acceleration responses and the canard deflection commands are clearly observed in the initial transient process,leading to the degradation of the achievable performance of TLPIRA. The above simulation results show the superiority of the proposed controller over the conventional TLC controller as well as the two-loop PI regulator autopilot.
The simulation results of the ISMC,including the acceleration responses and angular rates are shown in Figs.17 and 18.As seen,in the absence of the accurate estimation of and compensation for lumped disturbances by the model-assisted ESO,the tracking performance of the ISMC degrades compared with Figs. 4 and 5, and there exist overshoot and oscillations in each channel. This result demonstrates that the ability of the ESO to obtain an accurate estimation of uncertainties can effectively contribute to the better disturbance rejection performance of the proposed model-assisted ESO-based ISMC. Moreover, it can be concluded by comparing Figs. 17 and 18 with Figs.14 and 15 that the ISMC still performs better than the conventional TLC controller even though the observers are discarded.Comparisons of tracking errors in the acceleration loop and the angular rate loop for different methods are shown in Fig. 19. It is clearly observed that the tracking errors of the closed-loop system with the proposed controller are bounded and well within the small neighborhood of origin.As compared with TLC, TLPIRA, and ISMC method, higher accuracy and better disturbance rejection ability can be assured for the proposed method in spite of multiple disturbances. Such performance can be attributed to the ability of model-assisted ESOs in obtaining an accurate estimation of the uncertainties dynamics in time,and thus the nominal tracking performance can be recovered as a consequence of the effect of uncertainties have been effectively compensated for via model-assisted ESOs.
6. Conclusions
(1) The nonlinear cross-coupled acceleration dynamics are established to facilitate the design of the acceleration tracking controller,where the assumption that the angle of attack and the angle of sideslip are measurable is removed.
(2) With known model information of the guided projectile,the designed model-assisted extended state observers provide an accurate estimation of and compensation for the lumped disturbances and thus enhance the disturbance rejection performance of the compound controller.
(3) By integrating the techniques of the integral sliding mode and the sigmoid-function-based tracking differentiator into the ESO-based TLC framework, the proposed controller can not only eliminate the peaking phenomenon of the conventional TLC but also achieve quick and accurate tracking of pregiven reference signals, with a good decoupling performance and a strong robustness.
(4) Extensive simulations and comparisons with existing controllers in the literature are presented to demonstrate the superiority of the proposed controller in terms of its tracking performance and anti-disturbance capability.Further efforts can be made in stability analysis of spinning glide guided projectiles with an autopilot considering the phase lag and the response accuracy of actuators.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This research has been supported by the Fundamental Research Funds for the Central University(No.30919011401).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Design and experimental study of a new flapping wing rotor micro aerial vehicle
- CFD/CSD-based flutter prediction method for experimental models in a transonic wind tunnel with porous wall
- Prediction of pilot workload in helicopter landing after one engine failure
- Study of riblet drag reduction for an infinite span wing with different sweep angles
- Modulation of driving signals in flow control over an airfoil with synthetic jet
- Strong interactions of incident shock wave with boundary layer along compression corner
