Gaussian fitting based optimal design of aircraft mission success space using multi-objective genetic algorithm
2020-02-24YuanGAOYongliangTIANHuLIUXueSUN
Yuan GAO, Yongliang TIAN, Hu LIU, Xue SUN
School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China
KEYWORDS Evaluation;Gaussian fitting;Genetic algorithm;Mission success space;Neural network;System-of-systems
Abstract In order to obtain the optimized aircraft design concept which meets the increasingly complex operation environment at the conceptual design stage, System-of-systems (SoS) engineering must be considered.This paper proposes a novel optimization method for the design of aircraft Mission Success Space (MSS) based on Gaussian fitting and Genetic Algorithm (GA) in the SoS area.First,the concepts in the design and evaluation of MSS are summarized to introduce the Contribution to System-of-Systems (CSS) by using a conventional effectiveness index, Mission Success Rate(MSR).Then,the mathematic modelling of Gaussian fitting technique is noted as the basis of the optimization work. After that, the proposed optimal MSS design is illustrated by the multiobjective optimization process where GA acts as the search tool to find the best solution(via Pareto front). In the case study, a simulation system of penetration mission was built. The simulation results are collected and then processed by two MSS design schemes(contour and neural network)giving the initial variable space to GA optimization. Based on that, the proposed optimization method is implemented under both schemes whose optimal solutions are compared to obtain the final best design in the case study.
1. Introduction
Since Admiral Owens1introduced the System-of-Systems(SoS) concept into the military research, SoS engineering has been widely applied and investigated in military multidiscipline optimization areas; moreover, military departments and industries have always been focusing on the SoS effectiveness of new equipment at the conceptual design stage.2-6For now aircraft conceptual designers have to face many challenges in the context of SoS, since future combat environment (netcentric operation,4multi-domain warfare for example) goes extremely complex and the conceptual design stage primarily determines the whole aircraft design process;it will be a heavy cost even the aircraft design can be withdrawn if the requirements of future combat are not comprehensively considered at the aircraft conceptual design stage.
Regarding the evaluation research of SoS effectiveness, Biltgen5systematically proposed capability-based technology evaluation process for SoS where the macro weapon capability requirements can be quantitatively transformed into mission effectiveness indices.Artificial Intelligence(AI),surrogate model,simulation, K factor etc. are employed to research the impact of main design parameters and new technologies on SoS. Furthermore,Ref.6reviewed some other evaluation processes in the past two decades,like missions of a single design object in SoS,7a generic process to design new aircraft in a fleet,8design and allocation problem Technology Impact Forecasting (TIF) environmental creation and technical scenarios evaluation process9.
More specifically,quite a few scholars have examined the contribution effectiveness issues,both equipment-oriented evaluation and combat capability contribution.Gonzales et al.10studied the contribution effectiveness(kill ratio)of Link 16(on the F-15 s)to find the relation between increase in combat effectiveness and the Link 16 capability.Zhao and Li11established the network evaluation model of armament SoS based on the interactive relations among weapons and then calculated the contribution of weapons to SoS.Similarly,based on operation loop,an equipment offering degree evaluation method for Weapon System-Of-Systems(WSOS,a high-level weapon system)is proposed in Ref.12to evaluate the contribution of single equipment in WSOS. Further,Ref.13utilized the contribution evaluation of SoS to select the weapons system portfolio by establishing a hierarchical multicriteria value model for contribution quantification.
However,none of above literature has defined mission success in Effectiveness Index Space (EIS) for the SoS contribution effectiveness evaluation. For that purpose, Ref.14proposed the Mission Success Space (MSS) concept and utilizes the Mission Success Rate (MSR) to derive the contribution of certain equipment to SoS effectiveness whose potential applications should not be restricted to aircraft.Contribution to System-of-Systems (CSS)is noted in that study to demonstrate the executive level of equipment(or combat capability)in the future SoS combat.This paper continues to focus on the MSS based evaluation of contribution effectiveness to SoS, aimed at using Gaussian fitting technique and Genetic Algorithm (GA) tool to find the optimal MSS design according to the quantitative analysis of CSS results.
The paper is organized as follows:Section 2 will give the fundamentals in MSS based design and evaluation.After that,Gaussian fitting mathematic model is introduced as the basis of the following optimization work. Furthermore, GA tool and multiobjective optimization process are systematically illustrated in Sections 4 and 5 to introduce the proposed methodology.Finally,one simulation case is given in Sections 6 and 7 for method verification based on two different design schemes of MSS.
2. MSS based design and evaluation
2.1. Mission success space
MSS is a space defined as a part of EIS,the other part in EIS is named as Mission Failure Space (MFS). The boundary of these two parts is expressed as a function of design variables in the studied system, called Mission Success Function(MSF). In practical applications, Mission Success Condition(MSC) should be pre-set to determine the relative positions of MSS and MSF. After that, MSS is fully designed and MSR can be derived accordingly.
In order to quantify the mission success evaluation process,a novel effectiveness index (0-1 logical variable) in MSS is defined as:

where fE,jis Mission Success Effectiveness (MSE), Ejis the value of a conventional effectiveness index, and fF,jis the corresponding value of MSF.v1,v2,···,vmare m capability design variables considered in a combat mission. fE,j=1 means the mission is successful; otherwise, the mission fails. Therefore,‘‘Ej(v1,v2,···,vm)≥fF,j(v1,v2,···,vm)”is the MSC which gives the criterion for mission success. Here, for MSCs used in the simulation case (Sections 6 and 7), Ejis the Number of Destroyed Target (NDT) which assumes to be larger than or equals fF,j.But the correlation of fF,jand Ejin MSC is not necessarily to be ‘‘larger or equal” for other practical cases.
All above concepts and definitions are designed for giving the success criterion to the evaluation of specific combat missions. As shown in Fig. 1, in a multi-effectiveness studied system, MSF and MSC should be given for each selected conventional effectiveness index (Ej) with regards to all m design variables.Then,every Ejin EIS can get the corresponding MSE values using Eq.(1).If all MSEs equal 1,this mission performance(vi,Ej)can be accredited to be successful(the final MSE fE,fequals 1);otherwise,(vi,Ej)should be marked as failing(fE,f=0).The point-set definition of MSS using(vi,Ej)can be found in the Section 3 of Ref.14no more details.
The following subsection will discuss how to calculate MSR based on above MSS definitions.
2.2. Mission success rate
MSR is a ratio index which needs to be computed by division.Simulation cycle is a common approach to give the solution of MSR whose denominator is the simulation times and numerator is the times of mission success. Thus, MSR can be defined as:where φTis the MSR in a mission T, NS1_Tis the total simulation times of this mission, and NS2_Tis the simulation times in which the mission is accredited to be successful (fE,f=1).

Using the final MSE discussed in the last subsection, the numerator of MSR can be directly computed by accumulated fE,fwhich is used to denote mission success/failure at each time(t) of simulation:

Noting that there is usually much uncertainty in the practical studied systems and Ejvaries with the same design variables (vi), thus MSR results may differ when simulating the same system at different times though MSS designs are confirmed initially and stay unchanged.From the authors’experience in Ref.151000 is given to NS1_Tin a simulation cycle to compute MSR because in that case exercising the same system for different cycles will have little effects on mission effectiveness results.
2.3. Contribution to System-of-Systems
As discussed, CSS is a novel high-level index to quantify the contribution to WSOS and defined in specific combat missions.Ref.16lists 6 Measures of Effectiveness (MoEs) to ascertain how well the various fighter options (to replace the CF-18 in Canada) provide the effects needed to meet the requires of Aerospace Capabilities (ACs). 6 MoEs are all high-level indices of aircraft’s effectiveness, when put in a missionspecific context.But the object of aircraft’s contribution in that paper is AC, rather than the combat WSOS here.
Ref.14gives an effective method to derive CSS based on MSR calculation. This paper continues to use the same way comparing different combat SoSs where engagement of the studied equipment is the unique difference.
As shown in Fig. 2, the comparing thinking to calculate CSS is reflected in two different loops of combat simulations for the SoS with and without the studied weapon(combat aircraft)based on which MSR is computed using Eq.(2)for each group. After that, CSS can be briefly defined as:

2.4. MSS design for CSS evaluation
As discussed above,for the same studied system,various MSS designs can give multifarious success criteria thus MSR and CSS results would be different. In fact, the MSS design is to give a suitable MSF as the boundary of MSS and MSF in order to judge the success when getting Ejvalues. Therefore,Ref.14particularly represented designed MSFs to give and compare different success criteria. However, that paper only provided three MSS solutions to calculate CSS. Based on the analytical Gaussian fitting of CSS,this paper explores the possibility of searching the best MSS design in a space by using multi-objective GA tool(will be discussed in Sections 4 and 5).
Further, K part is defined here as a design point/line/surface(vi,fF,j)in MSS and expresses MSF in a simpler way which determines the change of success criterion with regards to the design variable (vi) in EIS. A clear example (K point) can be found in Section 6.2.1 of Ref.14As shown in Eq.(1),the effectiveness results(vi,Ej)generated by simulation should be compared with the related K parts before finally being accredited to be successful.
3. Gaussian fitting model

Fig. 2 CSS calculation using two simulation cycles.
This section will give the details of Gaussian fitting model to bridge the gap between CSS results and GA optimization objectives.Namely,in the optimization process,this model can automatically generate CSS fitting performance(GA objective)after getting the CSS data from simulation and MSS design.
From authors’ former studies, OriginPro is a powerful software which can not only plot clear, dedicated and databased figures but analyze the given data(interpolation, fitting,signal processing etc.). This study continues to focus on the empirical fitting analyzer in OriginPro and the used 2D Gaussian function is

where x and y are independent variables, z is a function of×and y. There are 7 undefined coefficients whose ranges need to be confirmed before fitting discrete points: z0, A, x0,y0, ω1, ω2, θ.
When giving 3-dimensional matrix data(x,y,z), the OriginPro analyzer can find the fitted 2D function ‘‘^z=f(x,y)”automatically by using the ‘‘Gaussian2D” in the ‘‘nonlinear surface fit” column. However, it is not clear how it defines the initial ranges of 7 variables and gives the final fitted results.In addition, it is unrealistic to open the software and use the analyzer for every different design point during the optimization process as we usually have thousands of design points for an optimization problem. Therefore, in this study, the Gaussian fitting is implemented in Matlab using a mathematic approach based on the embedded ‘‘fit” function17to ensure that the Gaussian fitting performance can be obtained in seconds for each design.
The ‘‘fit” function in Matlab can create a fit to the given data using the algorithm options specified by the ‘‘fitoptions”object where the fitting method (non-linear least squares, for example), ranges of coefficients, start point are predefined.Regarding the‘‘fittype”setting,Eq.(5)is chosen as the specific Gaussian function for the following fitting work. In addition,for the initial values of 7 design variables in Eq. (5), the ‘‘fit”toolbox selects default initial values for them uniformly at random from the interval (0,1).17
It is important to notice that the ranges of these coefficients are predefined by trial-and-error and stay unchanged for all the optimization work thus the fitting performance of all designs can be given in a uniform fitting criterion.These ranges are given in Table 1.
As mentioned, the Gaussian fitting codes are programmed in MATLAB where the ‘fit’ function is called for each design point and then output the corresponding fit performance.Therefore, the input of the established Gaussian fitting model is a 3D matrix(CSS data,based on a certain MSS design);the outputs are performance indices including R2, Root Mean Square Error(RMSE),Sum of Squares due to Error(SSE)etc.
Another key point in this study is the multi-objective genetic algorithm (GA) to search the best design of aircraft MSS according to objectives in GA.The following section will introduce the used GA and Pareto front technique.
4. Multi-objective GA and Pareto front
As will be discussed in Sections 5 and 6, this study has two objectives in the GA optimization problem which are both from Gaussian fitting performance. Two objectives are conflicting with each other thus it is unrealistic to find a solution that can optimize both objectives. Therefore, Pareto optimal front is usually employed for the Multi-Objective Optimization Problem (MOOP) to generate a set of design points as a balance of all objectives.18Pareto MOOP definitions and mathematic descriptions can be found in Ref.19This study utilizes GA to first find the Pareto front set and then introduce a new index (in Section 6.2.1) to choose the final best solution.
A simplified MOOP of this study is depicted in Fig. 3 with its inputs and outputs. This figure shows the basic process of generating Pareto front in which the boundary of the feasible domain (the area in purple) and the Pareto front location are depicted on the right side, optimization results. On the other side,it shows a simplified GA optimization process.First,simulation raw data for mission success evaluation should be collected.Then,MSF and MSS can be defined by design variables(Inputs) of GA thus CSS data will be obtained by using Eqs.(2) and (4). After that, based on the established Gaussian fitting model in the last Section,objectives(Outputs)in GA optimization could be generated. In manually set generations, the multi-objective GA can explore the feasible domain and finally get the Pareto front set (subject to constraints).
It is noted that each MSS design corresponds one design point. Therefore, in the design space of MSS, there would be large numbers of feasible designs. To give the Pareto front in limited computation, GA is applied as the search algorithm since it is an evolutionary algorithm that can get the convergence solution very fast.20,21There are three GA operators including selection, crossover and mutation to give the input of the next generation based on the current input and fitness.At each generation, individuals (parents) selected from the population following Pareto domination rules are crossed and mutated to create new individuals (children).21
In this study,‘‘gamultiobj”function in Matlab22is called to implement the multi-objective GA searching optimum in a certain design space of MSS. In this interface function, design ranges, population size, generation number and Pareto fraction can be manually set for specific MOOPs. However, the main function (which is case-specific, see Section 5) of this study should be coded separately to ensure that each MSS design can obtain new CSS data and then generate the corresponding Gaussian fitting performance. The following sectionwill focus on how multi-objective GA works in the optimal MSS design process.

?
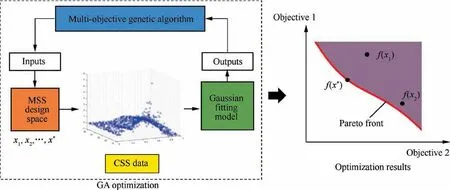
Fig. 3 Illustration of the studied MOOP.
5. Optimal design process
This study utilizes Pareto multi-objective GA to search the best design of K part according to the values of two objectives.Both objectives are index of Gaussian fitting, specifically,one is the R square (R2, the bigger the better), the other one is the Sum of Squares due to Error (SSE,the minimum is preferred).As GA optimization is usually to find the minimum of the objectives by default, this study sets 1/R2and SSE as the final two objectives which are the outputs of the studied MOOP, as shown in Fig. 4. It is noted that the best MSS design can be optimized according to the characteristic analysis of either MSRs or CSS;however,this paper only considers the Gaussian fitting performance of CSS as the optimization objectives. The reason is that, as shown in the cases of this paper and Ref.,14all MSR and CSS data obviously follows the Gaussian distribution and R2in some of MSR data can even be larger than 0.94. Therefore, this data character must be an important attribute of CSS results. Besides, this evaluation method can be applied as long as the effectiveness value has the increase trend followed by decreasing.
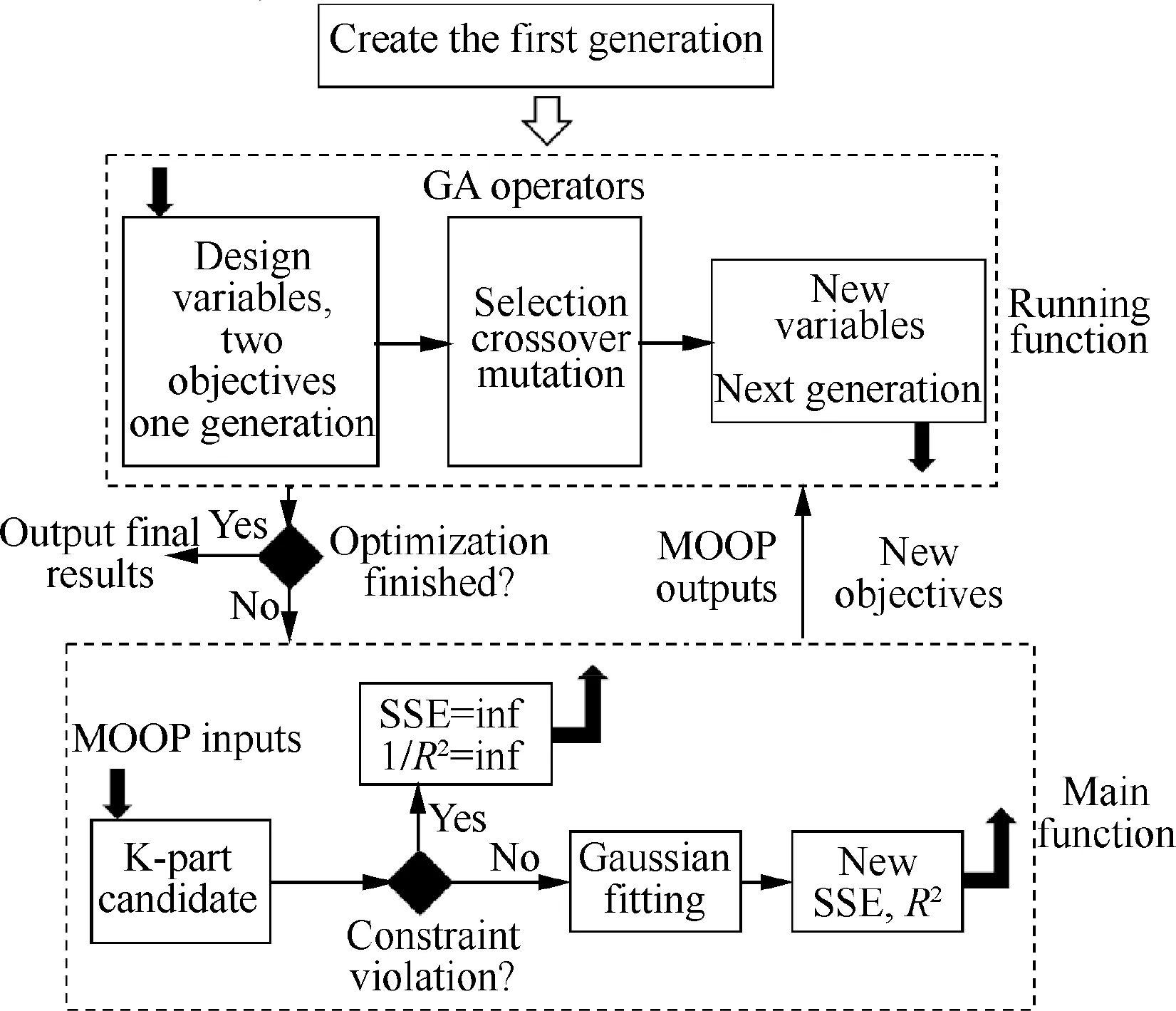
Fig. 4 Optimization procedure based on multi-objective GA.
To start the MSS optimization,the first generation of chromosomes should be created after setting the GA operators.The operator parameters are gap rate, recombine rate and mut rate, respectively.21GA users can give different values to these parameters but in this study default values are applied for the sake of convenience. As the number of objectives are two not one, more GA parameters (e.g. Pareto fraction)should be confirmed before running this algorithm.After that,we can give the population size and maximum generations to confirm how long the optimization process should be.
Fitness of individuals (parents and children) here consists of the values of two objectives whose weighting factors are set equally for GA operation. Fig. 4 summarizes the overall optimization procedure. The upper part of Fig. 4 shows the running function of ‘‘gamultiobj”; the below rectangle depicts the main function of this study.
In the running function,a new generation of chromosomes which maps the variables can be created by the three operators after ranking the fitness of the current generation (parents). If the iteration times does not exceed the pre-set maximum generation number, individuals of parents should go to the main function until reaching the maximum number.
In the main function,the fitness of the new generation(children)should be obtained by the Gaussian fitting model for the next selection of chromosome population (children of children). However, before running that model, the K-part candidate which is determined by design variables should be checked by constraints. If constraints violate this new design,their objectives will be assigned the infinite values and this design will stay at the bottom of the fitness ranking in the new generation.If not,the Gaussian fitting model can give fitting performance of this design as its objectives in GA optimization.
The following Sections 6 and 7 will introduce the case study regarding modelling and simulation to validate the proposed optimal design method. The simulation system was built on the simulation platform, Anylogic, based on Agent theory23which is a crucial concept in the field of Distributed Artificial Intelligence (DAI).24
6. Simulation case
The studied case is to validate the proposed design method of MSS using the Gaussian fitting model and GA optimization.The scenario is aircraft penetration mission(represented by T)confronting with ground radar defense system.A transient diagram of the simulation virtual scene is shown in Fig. 5. The Red side includes six fighters and a jammer.The Blue includes three sets of land-based air-defense systems (Radar) and six military targets. Except for the key design variable of the fighter,Radar Cross-Section(RCS),14,15combat velocity(vkill)is another significant factor for the mission success of T which should be involved in the aircraft capability variable for the MSS design. The aim is to quantify the contribution of the Electronic Warfare Aircraft(EWA,the jammer)to the combat SoS based on the CSS evaluation (see Section 2).
6.1. Modelling and simulation
Six fighters try to penetrate the radar defense and then kill all military targets;therefore,radars are not regarded as their targets in this mission. All fighters can operate the penetration mission independently and they share the battlefield situation with each other to finish the same mission which demonstrates the characteristics of SoS concept.6
6.1.1. Agent model
There are six agents built in this combat system including fighter, Jammer, Air-to-Surface Missile (ASM), radar,Surface-to-Air Missile(SAM)and military target.Fig.6 shows the state charts of Fighter, SAM and Radar agents in T.Assuming that the initial precise position of the target is unknown to the fighter fleet,they first fly to the assumed target location at the cruise velocity. When the distance of the assumed target is smaller than 1000 km,they entry the combat field with a new velocity.After the first radar is detected,all of them speed up to the combat speed (vkill) synchronously to penetrate the radar defense.Then,at this combat velocity,they finish the penetration mission by killing all military targets before returning to base.
If the fighter reaches the range of air defense system, radar will launch a SAM to attack the fighter.As shown in Fig.6(a),the fighter will evade the coming enemy SAM when it meets the entry condition of ‘‘Escaping” state. During the‘‘MoveToTarget” state, the fighter will not evade the coming SAM since fighter needs to penetrate the radar defense range and kill the target in time, which will increase the hit rate of SAM. It is worth noting that after the fighter is destroyed by SAM,the military target which was initially distributed to this fighter should be retargeted to other fighters.That is the function of ‘‘Retarget” or ‘‘Retarget 1” states.
SAMs are launched by radar agents when meeting the launch condition. As shown in Fig. 6(b), the state logic of SAM is very simple including two relatively independent parts after the state of ‘‘Flying” where the missile is flying to its assigned target (fighter). When the distance between SAM and this target reaches 30 km, the state is divided into two parts which depends on whether the fighter is evading this missile or not (see the ‘‘Escaping” state in Fig. 6(a)). When the fighter is in the states of attacking targets at the point of 30 km, it will not enter the ‘‘Escaping” state while, synchronously, the SAM will enter the state of ‘‘TargetsAttack”.It should be noted that there is also a ‘‘threating rate” related to this division, which means that entry of ‘‘TargetsAttack” is not up to the real-time state of fighter only. These two parts definitely have different hit rates of attack and the rate of‘‘TargetsAttack” is higher than that of ‘‘isThreating”; however,both of them cannot completely guarantee the attack success of this missile.
The state logics of radar and other agents in the simulation system are relatively simple. The same modelling details of those agents can be found in the Section 6.1 of Ref.,14no more details. Different from that paper, here there is no UCAV in the Red side and fighters try to penetrate the radar defense systems rather than attacking them.
6.1.2. Design of simulation experiment
The input values of two variables originate from Monte Carlo sampling in Anylogic based on the data ranges rather than the uniform sampling. The total number of design points in this two-variable case is 1000. Data ranges of these two variables are shown in Table 2. The simulation experiment is exercised on these 1000 design points one by one. For each design,two simulation cycles (1000 times per cycle) are carried out to compute MSRs and CSS of Jammer after MSS/MSC is confirmed. The only difference between these two cycles for each design point is the engagement of Jammer in the simulation.Regarding different design points, two variables vary but the other parameters/factors (scenario, missile speed, radar location etc.) always stay the same. There are six military targets to be killed, the initial MSC is killing all targets which means NDT equals 6.If there is a Jammer in the fleet,the radar detection capability will be reduced by 30%.

Fig. 5 Transient diagram of penetration simulation scenario mission.

Fig. 6 State charts of fighter, SAM and radar agent.
6.2. Simulation results and K-part candidate design scheme
Based on the initial MSC, MSR results of all 1000 design points can be generated after two simulation cycles, as shown in Fig. 7. In both figures, there is a clear decrease trend of MSR (calculated by Eq. (2)) as RCS increases or vkillgoes down. These simulation results will be used for the following optimal MSS design work instead of exercising the same simulation more because as mentioned in Section 2.2, the MSR and NDT results will change little when giving 1000 to NS1_T.
In this study, several core candidates of K part (for NDT=5,fF,jin Section 2)and the ranges of design variables in GA optimization are given by two different design schemes:1.contour map of MSR results;2.Neural Network(NN)Pattern Recognition (PR).25It is noted that one contour map in Fig. 7 can only generate 7 sets of points according to certain features of MSR data, based on that, the core K-part candidates are set as the 7 middle fitting curves of these feature points. Regarding NN PR design scheme, training a network is the first step followed by analyzing the PR value distributions to give the core K-part candidates.
It is important to notice that the potential MSS design scheme should be primarily investigated to make sure thatthe resulting MSS design candidates are reasonable. In this case, as will be shown in Section 7.2, the bottom-right design area in the 2D design space should have higher possibilities than the up-left area for being a part of MSS of lower NDT because the up-left area has better RCS and vkillthus its MSC should be stricter.
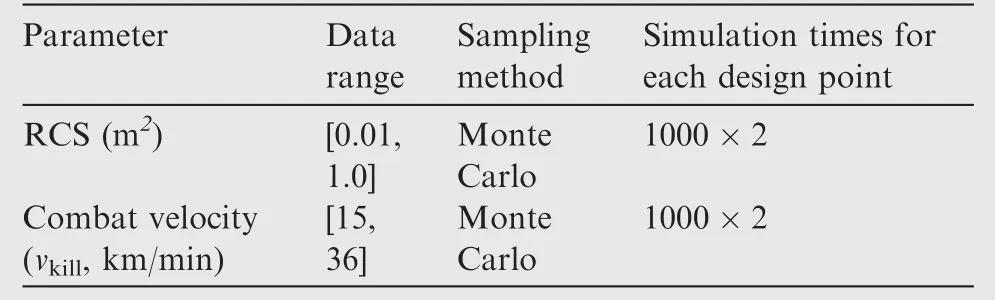
Table 2 Input of two design variables in simulation experiment.
6.2.1. Contour results
As shown in Fig.7,one solution of giving the initial K parts is designed to be contour lines in the MSR contour map with original MSS design. Both figures have 7 contour lines and the values of corresponding two contour lines (shown in the color scale bars) are very close.
In this study, the contour solution utilizes quadratic polynomial fitting lines to instead the original data of contour lines(generated by contour makers in OriginPro) since the original data are plenty of points which are not convenient for MSS design. The serial numbers of 7 fitted contour lines are shown in each contour map of Fig. 7.
After finding the 2×7 fitted polynomial lines, 7 core Kpart lines can be given by getting the middle lines.Here,middle line refers to a line in the middle of two given lines where for every x-coordinate, y-coordinate of the point on this middle line is the average value of two y-coordinates on the two given lines. Therefore, each pair of fitted polynomial lines that have the same serial number in No Jammer and With Jammer contour maps can give one specific middle line. The generation method is simply calculating the mean value of three coefficients from the two polynomial lines and use three mean values to form a new quadric expression for one middle line. All 7 middle lines as well as their related contours are shown in Fig. 8. The authors utilize these middle lines (new K parts)to give the boundary of MSS for‘‘NDT=5”for the following GA optimization work where the success criterion is changed from ‘‘NDT=6” to ‘‘NDT>=5”.
Table 3 shows the coefficients of 7 middle lines and the fitting performance using the Gaussian fitting model. a0is the quadratic coefficient, b0is the primary coefficient and c0is the constant term. As there are two objectives in the GA optimization which could not determine the best design,this paper introduces another index, F value, to integrate two objectives into one for the best choice after the Pareto front is obtained by ‘‘gamultiobj”:

Fig. 7 MSR Contour results based on initial MSC (NDT=6, killing all targets).

where

The F values of 7 core K-parts in the contour-map design scheme are also shown in Table 3.Comparing these 7F values,No.3 middle line should be the best one as it has the maximum F value. This study utilized the coefficients of these 7 polynomial lines to provide the initial ranges for the design variables(MSS designs, MOOP inputs) in GA optimization, namely there are three design variables and their ranges are given by a0, b0, and c0values in Table 3.
6.2.2. NN based pattern recognition
Except creating contour results for the generation of initial Kpart candidates, this study utilized NN PR as another design scheme training the simulation data to give new K-part candidates for the optimal MSS design.
As shown in Fig. 9,the used NN tool is built with normalization functions at the inputs (i) and softmax functions26at the outputs (o). There is one hidden layer whose neurons are marked in green,weights and biases are omitted for simplicity.Analytical formulation for the NN PR model is constructed by using this 3-layer feedforward network whose hidden layer has 10 neurons.In particular,this network represents the following relation:

Therefore, the input data of training NN includes two design variables and one effectiveness index (NDT) which comprehensively reflects the non-linear relations between typical NDTs and design variables in the detailed simulation system. On the other hand, the output of proposed NN is just pattern/classification labels (0 or 1) of two situations:‘‘NDT=6” and ‘‘NDT=5” since we want to recognize the difference between these two sets of NDT data.
Regarding the training data of NN, this study chose the simulation raw data sets of ‘‘NDT=6” and ‘‘NDT=5”(marked as input_N6 and input_N5, 1000 samples for each)where the 2-element output is (1, 0) for the former and (0, 1)for the latter. Noting that both sets are from the simulation cycle of the studied system with Jammer(Wk).NN was trained using the Neural Net Pattern Recognition in MATLAB. The training only costs 2 seconds with 67 epochs and the prediction accuracy of raw simulation data is 99.775% (with output PR values rounded up).
It is important to notice that when we give input values or matrix to the trained NN tool,the output would be continuous not just two integers because the NN tool is established in analytical approach thus there is no strict limitation for the input data. Based on that, we can easily find out a desired part of raw data set according to PR values (NN output, [PRN6,PRN5]) to show how far ‘‘NDT=6” is different from‘‘NDT=5”. Fig. 10 shows the PR validation results of two raw data sets using the trained NN tool which directly give the distributions of PR value in terms of RCS and vkill.
After the training, this study only utilized the PR value of‘‘NDT=6” (PRN6, the first element in NN output) to give the desired K-part candidates based on the high-density uniform sampling in the whole 3-dimentional input space of NN (see Eq. (8)). As shown in Fig. 11, four data sets are extracted from the PR value distribution in the plane of‘‘NDT=0”. This study selected the bottom-right boundary fitted lines of these four sets as the core designs of K-part candidate followed by giving design variables to GA optimization.
Table 4 shows the MSS design results of NN based K-part candidates.In order to pursue the high fitting R2performance(larger than 0.98) of four boundary lines, NN based K-part candidates are generated by quadratic polynomial fitting rather than using linear lines. The same with the contourbased candidates (Section 6.2.1), this study utilized the coefficients of these 4 polynomial lines to give the initial ranges for the design variables in GA optimization.Next section will discuss the ranges of GA design variables and the optimization results.

Fig. 8 Middle lines generated by contour lines.

Table 3 MSS design results based on contour map.
7. Optimal design of MSS using GA
7.1. Optimization formulation
Based on the 7 contour-based K-part candidates and 4 NNbased candidates discussed in Section 6,initial ranges of design variables were determined to do the multi-objective GA optimization. Since all above K-part candidates are quadratic parabola, in the optimization we continue to use quadratic equations to represent potential MSF designs for‘‘NDT=5”.Namely, every parabola in the 2D space can be a potential MSS design and the resulting CSS should be different as long as this MSS design (MOOP input) can satisfy constraint condition(s) of optimization. Based on that, three coefficients in the quadratic equation are further extracted to be the design variables in GA operation.Different from two design variables in simulation experiment (Section 6.1.2), they are variables in optimization and at this stage,simulation experiment has been done whose data stay unchanged and serve as the basis of GA optimization.

Fig. 9 Used NN schematic for pattern recognition.

Fig. 10 PR results using trained NN tool.
The selection method of variable range is simply to choose the minimum and maximum values of each variable from the initial K-part candidates.The variable ranges using two different schemes are shown in Table 5. Ranges from two design schemes on three variables are not fully overlapped, so it is worth of exploring both design schemes and compare their optimization results.
There is only one constraint built in the GA optimization model: the quadratic functions in selection pool must have at least one intersection with the 2D space of RCS and vkillgiven by Table 2. This constraint is set as a hard condition which means if a potential parabola violates it, its two MOOP outputs will be set infinite values to make sure that this design will be at the bottom of the fitness ranking in GA optimization(see Section 5). It is noted that if an MSS design cannot meet this condition, it means all points in the 2D space of RCS and vkillare either in MSS or in MFS for ‘‘NDT=5” which will lose the significance of creating a new MSS design for‘‘DNT=5”.That is the reason why we set this constraint condition for GA optimization.
7.2. Optimal design results
The optimization results are obtained from running the multiobjective GA with a population size of 100 and 100 generations in Matlab for each design scheme of variable range.Namely, there are totally 100×100 candidates designed during the optimization process. Among that, in contour-based optimization, 1097 candidates are violated by the constraint and for the other 8903 candidates, Gaussian fitting model is exercised to output the two objective values,1/R2and SSE.By contrast,for NN-based optimization,all 10,000 candidates are feasible designs as the variable ranges are relatively small.

Fig. 11 PR value distribution of input_N6 in the plane of NDT=0.

Table 4 MSS design results based on NN PR.

Table 5 Variable ranges for GA optimization.
The next two sections will present the Pareto front and the best design in two design schemes. Regarding the F value calculation, this study utilizes 0.7 as, and 300 as SSEmaxfor both schemes.
7.2.1. Contour-based optimization results
After contour-based GA optimization,the Pareto front can be obtained automatically by the ‘gaoptimset’ function. Among the design points in the final Pareto front (50 can be collected from Matlab), four points are selected whose variable values,objectives and numbers of points in MFS/MSS are shown in Table 6 (other points are located very close to them). Seen from the F values of these four design points,No.1 is the best chosen by contour-based multi-objective GA optimization since its F value is the biggest among the Pareto-front points.
Regarding the best design and F value calculation,the final MSS distribution for T of 1000 data points on the top view is presented in Fig.12(a).The black line is the K part of the best design generated by using a0, b0, and c0as the coefficients of quadratic function.It is the boundary of MSS for the effectiveness ‘‘NDT=5”. When the design point locates in the right bottom part, the success criterion should be ‘‘NDT>=5”rather than ‘‘NDT=6”. Fig. 12(b) shows the distribution of CSS results and its Gaussian fitting results based on that MSS. As the fitting R2and SSE of CSS data using the best design of contour map are 0.6596 and 224.006 (see Table 3),the proposed GA optimization method gives an excellent MSS design solution which has a better fitting performance(larger R2and smaller SSE) than 7 K-part candidates of contour design scheme.
7.2.2. NN-based optimization results
Using the same GA tool,the optimization results of NN-based design scheme can be obtained.There are several design points in the Pareto front,we select 7 points and put them in Table 7.Other points locate close to them or have the same objective values with them.The reason why there are many close design points in Pareto front is that simulations raw data is not much enough (only 1000) to distinguish the difference among these points.Due to the limited space,the MSS distribution and CSS results of these quadratic K parts are not depicted in this paper.
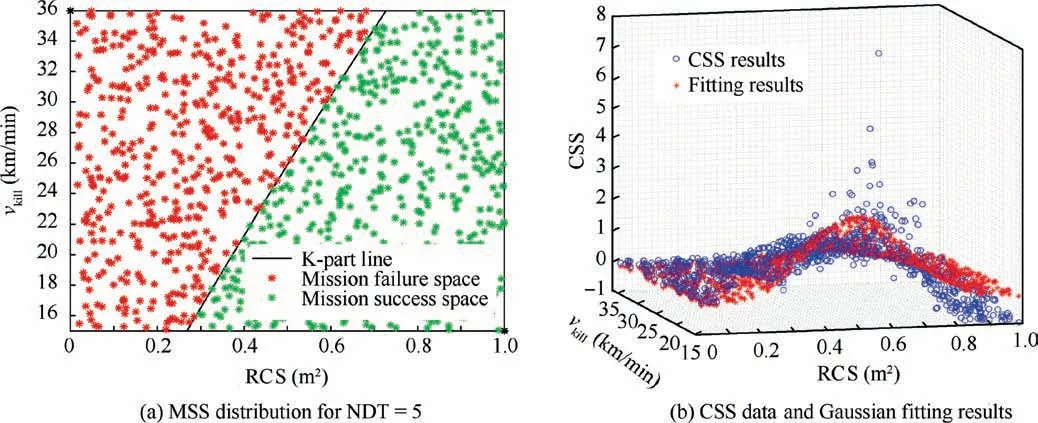
Fig. 12 The best design of the contour-based optimization.

Table 6 Pareto design results after contour-based GA optimization.

Table 7 Pareto design results after NN-based GA optimization.
Though these 7 Pareto front results are all better than the initial K-part designs in Table 4, the performance in this part is worse than the No.1 in Section 7.2.1(smaller R2and larger SSE);therefore,No.1 in the contour-based optimization is the final best solution of this case study. It is important to notice that even though the results here from NN-based design scheme are not good enough, NN provides an excellent way for giving potential K-part candidates. As the optimization results are case-specific, NN PR probably will work well in other cases.
In addition, both design schemes are only using quadratic functions to give K-part candidates for the optimization.Therefore, in the potential studies, linear function as well as other polynomial functions could also be utilized for giving K parts and corresponding design variables in optimization would vary.Though the proposed methodology does not limit the scheme of giving K parts, it utilizes the same Gaussian fitting model and GA function to find the best MSS design according to the fitting performance of CSS results.
8. Conclusions and future study
Using multi-objective GA optimization tool, this study proposes an optimal design approach for aircraft mission success space based on the analytical Gaussian fitting model. The analytical model is built in Matlab to support the following efficient optimization work. To generate the initial design ranges of variables in GA, this study utilizes two different methods to process the simulation raw data: contour map and neural network pattern recognition. After that, with the help of Gaussian fitting model, Pareto front results of both are obtained by the GA optimization tool as comparative studies. Finally, the No. 1 design in contour-based optimization is chosen as the best of this study according to a new index (F value) integrating two objectives in Pareto front.
The future study will design MSS based on multiple effectiveness indexes (including NDT) because deciders usually should take more than one key effectiveness into account for the mission success evaluation work.Among the interests,analytic hierarchy process (AHP) can be explored as a potential way for mapping effectiveness indices to the mission success.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Design and experimental study of a new flapping wing rotor micro aerial vehicle
- CFD/CSD-based flutter prediction method for experimental models in a transonic wind tunnel with porous wall
- Prediction of pilot workload in helicopter landing after one engine failure
- Study of riblet drag reduction for an infinite span wing with different sweep angles
- Modulation of driving signals in flow control over an airfoil with synthetic jet
- Strong interactions of incident shock wave with boundary layer along compression corner
