Intrinsic physical relationships between rotor modal shapes and instantaneous vibrational energy flow transmission characteristics: Theoretical and numerical analysis and application

Yingqun MA, Qingjun ZHAO,c,*, Wei ZHAO, Binbin LIU, Long HAO

a Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China

b School of Aeronautics and Astronautics, University of Chinese Academy of Sciences, Beijing 100049, China c Key Laboratory of Light-duty Gas-turbine, Chinese Academy of Sciences, Beijing 100190, China

KEYWORDS Energy balance relationship;Instantaneous vibrational energy flow;Rotor modal shapes;Rotor vibration attenuation;Structural intensity method;Transmission characteristics

Abstract The modal vibration of the rotor is the main cause of excessive vibration of the aeroengine overall structure.To attenuate the vibration of the rotor under different modal shapes from the perspective of energy control, the intrinsic physical relationships between rotor modal shapes and instantaneous vibrational energy flow transmission characteristics is derived from the general equation of motion base on the structural intensity method. A dual-rotor-support-casing coupling model subjected to the rotor unbalanced forces is established by the finite element method in this paper. The transmission, conversion and balance relationships of the vibrational energy flow for the rotors in the first-order bending modal shape, the conical whirling modal shape and the translational modal shape are analyzed, respectively. The results show that the vibrational energy flow transmitted to the structure can be converted into the strain energy, the kinetic energy and the energy dissipated by the damping of the structure. The vibrational energy flow transmission characteristics of rotors with different modal shapes are quite different. Especially for the first-order bending modal shape, the vibrational energy flow and the strain energy are transmitted and converted to each other in the middle part of the rotor shaft,resulting in large deformation at this part.To attenuate this harmful vibration,the influences of grooving on the shaft on the first-order bending vibration are studied from the perspective of transmission control of vibrational energy flow.This study can provide theoretical references and guidance for the vibration attenuation of the rotors in different modal shapes from a more essential perspective.

1. Introduction

With the increasing requirements of the thrust-weight ratio for aero-engines, during the overall performance design of the engine, the operating rotating speed of the rotor is usually set to a higher range to make a large thrust. In addition, in order to reduce the weight of the engine, besides the use of lightweight, high-temperature and high-strength materials,1it is also required to reduce the design redundancy of the components, as much as possible to explore the potential of existing structures and materials.2The overall performance scheme of high-speed and large-thrust and the overall structural scheme of low redundancy and high structural potential make the thrust-weight ratio of the aero-engine further improved, but also result in complex characteristics of rotor dynamics.Moreover,the casing is designed to be thinner and lighter to reduce weight,resulting in lower stiffness which enhances the coupled vibration between the rotor and the casing and the complex dynamics characteristics of the overall aero-engine.This makes the rotor vibration more easily to cause the overall aero-engine to vibrate, and the fault of the static-rotor rubbing3,4occurs,which affects the safety and reliability of the operation for aero-engines.

Therefore,it is necessary to combine the rotor and the casing to a rotor-casing coupling system to analyse its vibration characteristics. Many researchers have carried out a lot of investigations on the rotor-stator coupling dynamic modelling methods to improve the calculation efficiency and accuracy.5-9The rotor unbalanced force is the most important and common source of the excitation.10The engine passes the critical speeds of the rotor during the starting,stopping and even operating rotating speed range,which will cause excessive transient vibration of the rotor and the whole engine. There were also many studies focusing on the control and attenuation of the vibration of the rotors and the whole aero-engines utilizing the passive or active vibration control methods.11-14Although the passive control methods can lessen the faults caused by the resonant vibration of the rotor when passing the critical speeds,it does not fundamentally attenuate the vibration when the rotor resonates. The active control methods can change and avoid the critical speeds of the rotor within the operating rotating speed range by changing the inherent characteristics of the structure.Aero-engines,however,are required to install additional devices to achieve the change of supporting stiffness and damping, which increases the complexity and weight of the overall structures.

The propagation of vibration in the structure is essentially the transmission of vibrational energy flow.Therefore,in addition to the approaches mentioned above, the modal vibration of the rotor which is the main excitation source of the aeroengine can also be attenuated through a more essential approach, that is the transmission control of vibrational energy flow. There are two main branches of energy analysis method: Transfer Path Analysis15and Power Flow Method.16The former is mainly used to solve the issues of Noise, Vibration and Harshness(NVH)of the vehicles based on the experimental data. The latter is more widely used because it can predict more information of the vibration sources, sinks and transmission paths in vibrating structures. The structural intensity method, one type of the power flow method, is an effective and powerful method to study the vibration characteristics of structures from the perspective of vibration energy.This method combines the stress and velocity responses of any point in the elastic structure to characterize the vibrational energy flow per unit cross-sectional area and unit time in the structure,17-19the value of which represents the magnitude of vibration energy transmission at that point, and the vectors represent the transmission directions of vibrational energy flow. Therefore, the structural intensity vector field visualization technique can be used to describe the main transmission paths and distribution of the vibrational energy flow in a certain structure. Moreover, the structural intensity divergence fields can be used to indicate the sources and sinks of the vibration energy,20which can be used to directly analyze and judge the main sources of vibrational energy flow in the structure and the main dissipative positions, and provide vibration attenuation means from the three levels of vibration sources,transmission paths and vibration sinks.

The rotor, the main vibration source of the whole aeroengines, has different structural vibration characteristics and vibrational energy flow transmission characteristics under different modal shapes. Therefore, in order to control and attenuate the vibration of the rotors and the whole engines from the perspective of vibrational energy flow transmission,it is necessary to study and analyze the intrinsic physical relationships between the structural vibration characteristics and the vibrational energy flow transmission characteristics of the rotor under different modal shapes. Romano et al.21derived the relationship between the two through the energy balance relationship of the plate-shell structure without the influence of damping.It is found that the divergence of the structural intensity is related to the rate of change of kinetic energy and the strain energy. However, for the rotating parts such as the rotors of the aero-engine, the damping of the structure and gyroscopic moments may also participate in and affect the transmission process of vibrational energy flow. Therefore,the current study on the intrinsic relationship between the two cannot be applied to the field of vibrational energy flow transmission characteristics analysis for the rotors of aeroengines.

Based on this,this paper starts from the general equation of motion, considering the influence of the damping of the structure and gyroscopic moment, and develops the inherent physical relationships between the structural vibration characteristics and the vibrational energy flow transmission characteristics. The finite element model of a dual-rotorsupport-casing coupling system with the rotor unbalanced forces is established. The relationships between the modal vibration characteristics and the vibrational energy transmission characteristics of the rotor in the first-order bending modal shape, the conical whirling modal shape and the translational modal shape are respectively calculated and analyzed utilizing the developed simulation system consisting of the finite element tool and the in-house program. Moreover, the influence of grooving on the rotor shaft on first-order bending vibration is studied to attenuate this kind of harmful vibration.The findings of this paper can provide theoretical references and guidance for attenuating the modal vibration of the rotor from the perspective of transmission control of vibrational energy flow.

2. Analysis methods of vibrational energy flow transmission characteristics

2.1. Structural intensity method

The vibration energy is carried by the vibration waves and transmitted to various parts of the structure. Structural intensity method is an effective method to assess the vibration energy transmitted in structures. This method was developed by Noiseux17in the 1970s to transfer the theory of sound intensity in aerodynamics to continuum mechanics. Instantaneous structural intensity represents vibrational energy flow through an elastic medium per unit time and unit cross-sectional area,which characterizes the magnitude and direction of vibration energy transmitted in the structure.Its general expression combining the stresses with the particle velocities can be written as22:

where, Ii(t) is the component of the instantaneous structural intensity; σij(t)is the component of the stress tensor at a point where i is the normal direction of the area and j is the direction of this variable; vj(t) is the velocity in the j-direction at time t.The rotor shaft and blisk can be simulated by threedimensional solid elements, as shown in Fig. 1. For this type of element, the structural intensity indicates the vibrational energy flow at a given infinitesimal volume. Each of the solid element surfaces includes a direct stress in accordance with the normal direction of this surface and two shear stresses perpendicular to the normal stress and orthogonal to each other.The instantaneous structure intensity expression of the solid element can be extended to the x, y and z directions in the Cartesian coordinate system, and it can be obtained by combining the Eq. (1):

Fig. 1 Displacements and stresses for solid element.

2.2. Streamline representations of structural intensity field

The structural intensity field of solid elements is a threedimensional vector field. The streamline visualization technique is a powerful and useful tool to display the details of transmission or flow for a vector field. Generally, this technique is applied to the flow field display for a velocity vector field. Therefore, analogous to the definition of streamlines in the velocity vector field, the tangential direction of each point of each vibrational energy flow streamline is consistent with the direction of the energy flow vector at that point.Therefore,the streamline of the structural intensity vector field can be expressed as23:

where,r is the particle position;I(r,t)is the structural intensity in the particle position r at time t.

For the three-dimensional structural intensity vector field of the solid elements, the differential equation describing the structural intensity streamline is:

where i, j and k are three mutually perpendicular unit vectors(modulo=1) in the Cartesian coordinate system.

3. The transmission, conversion and balance relationships of the vibrational energy flow

The structural intensity method is used to analyze the structural vibration problem from the perspective of energy transmission. According to the Newton’s second law, the dimension of force is [M]×[L/T2]=[ML/T2]. Therefore, the dimension of stress is [M/(LT2)]. The dimension of velocity is[L/T]. Therefore, the dimension of structural intensity of solid elements is [M/(LT2)]×[L/T]=[M/T3] (M, L and T denotes the dimensions of mass, length and time, respectively). Base on the dimensional analysis, the characteristic parameters of structural vibration that are intrinsically and physically related to the structural intensity should also be the dimension of energy.Some scholars have carried out related research in this field. Romano et al. derived the physical relationship between the structural intensity and the mechanical energy through the energy balance relationship of the plate-shell structure, which is as follows21:

where, h is the mechanical energy density; I is the structural intensity vector; V is the total volume of a certain structure;dτ is the volume element; ∇is the Hamiltonian operator.

It can be seen from the above equation that at any point in the elastic structure,the divergence of the structural intensity is equal to the negative of the rate of change of the total mechanical energy of the structure.A negative value of the divergence represents the energy sink absorbing the transmitted vibration energy, a positive value represents the energy source releasing the vibration energy to the surrounding structures. Therefore,Eq. (5) shows that the vibrational energy flow transmitted to the structure is converted into the kinetic energy and potential energy (strain energy) of the structure; likewise, the kinetic energy and strain energy of the structure can also be converted into vibrational energy flow to the surrounding structures.

For the aero-engines, in addition to structural kinetic energy and strain energy, the damping of the structure and gyroscopic moments generated by rotating components are also involved in the transmission and conversion of vibrational energy flow in the structure. Therefore, this section will start from the general equation of motion,considering the influence of the damping of the structure and gyroscopic moment, to derive the energy balance relationship between structural vibration characteristic parameters and vibrational energy flow in the transmission and conversion process.

The general equation of motion in the stationary reference frame can be expressed as:

where, M is the symmetric mass matrix; K is the symmetric stiffness matrix; C is the damping matrix; G is the gyroscopic matrix; q is the displacement vector; ˙q is the velocity vector;¨q is the acceleration vector; fais the applied load vector.

Multiplying Eq. (6) by the velocity vector ˙q, further yields:

The first term on the left-hand side of Eq. (8) is the rate of change of the kinetic energy ˙Ev, the second term is the rate of change of the strain energy (or potential energy of elastic deformation) ˙Es, and the third term is the sum of the power dissipated by the damping of the structure and the power done by the gyroscopic moments PC+G.

For the term on the right-hand side of Eq. (8), it denotes the transmitted power to the structure through its closed surface.24Therefore,this term can be expressed in the tensor form as follows:

where,Pstris the transmitted power to a certain structure;A is the total surface of a certain structure;ds is the area element;njis the normal vector of the surface.

According to the Gauss’s theorem, Eq. (9) can be further expressed as:

Eq. (10) can be further expressed according to the definitions of the divergence and the structural intensity as follows:

It can be seen from Eq.(12)that the structural intensity and the structural vibration characteristic parameters are also connected by energy, specifically, the rates of change of kinetic energy and the strain energy, and the energy dissipated by the damping of the vibration structure. Moreover, for the forward synchronous modes caused by the unbalanced forces,the gyroscopic effect contributes negative kinetic energy. Therefore, in the calculation process, the influence of gyroscopic effect is counted in the change of structural kinetic energy.For any research object, the volume integral of the divergence of structural intensity at any time on this object is equal to the negative of the sum of the rate of change of the total mechanical energy and the energy dissipated by the damping of the research object. From the point of view of energy conservation, it can be seen that part of the vibrational energy flow transmitted to the structure is used to change the kinetic energy and strain energy of the structure, and the other part is dissipated by the damping of the structure.

4. Calculation model-A dual-rotor-support-casing coupling model

Fig. 2 Model of the dual-rotor-support-casing coupling system(HPR: High-Pressure Rotor; LPR: Low-Pressure Rotor).

Fig.2 shows the model of an aero-engine dual-rotor-supportcasing coupling system with rotor unbalanced forces. This model includes three casing structures (the compressor casing,the combustor casing, and the turbine casing), two rotor systems (the low-pressure rotor system and the high-pressure rotor system) and four supporting systems (bearings and struts). Two adjacent casings are combined by the flanges to transmit vibrational energy flow between them. Two mainmounts which are respectively installed on two horizontal sides(±90°) of the combustor casing and one vice-mount which is installed on the top(0°)of vertical sides the compressor casing is used to fasten this model. Four supports equispaced on the casing circumferentially at each bearing position to transmit the vibration energy between the casings and the rotors. The features of these two rotor systems are listed in Table 1.Moreover,in order to quantify the effect of the structural damping,the damping coefficient of each component is taken into consideration. The structure parameters of this model are listed in Table A1 in the Appendix A. And the material properties used are listed in Table A2 in the Appendix B.

Fig. 3 shows the finite element model of this coupling system, which is made up of different types of elements. 16640 four-noded shell elements with 16800 nodes are used to simulate the casing and the flanges; 37872 eight-noded solid elements with 44527 nodes are used to simulate the shafts and the disks (low-pressure rotor is simulated by 31872 solid elements with 35085 nodes; high-pressure rotor is simulated by 6000 solid elements with 9442 nodes);the blades are simplified by 4 mass elements with 4 nodes (the blades of each blisk are simulated by one mass element), and the mass, polar diameter moment of inertia and diameter moment of inertia for the blades are taken into consideration; the bearings and the supports are simulated by 16 spring elements with 32 nodes (each bearing is simulated by 4 spring elements) and 160 beam elements with 176 nodes (each support at each bearing position is simulated by 10 beam elements), respectively. The vibration sources of each rotor of this coupling model are two unbal-anced forces, which are respectively located at the centroids of the compressor blisk and the turbine blisk and are in phase.Each unbalanced force is decomposed into two transient sinusoidal forces at the centroid of the blisk in two orthogonal directions, which is simulated by the transient tabular force.In these two orthogonal forces, the rotor rotating speed, the unbalanced mass of the blisk (which has been listed in Table A1 in the Appendix A) and the initial phase of the unbalanced magnitude are taken into consideration, which simulates the actual load condition of the rotor unbalanced force. The excitation frequencies of rotor unbalanced forces of the low- and high-pressure rotors are 400 Hz and 500 Hz,respectively, corresponding to their design rotating speeds.

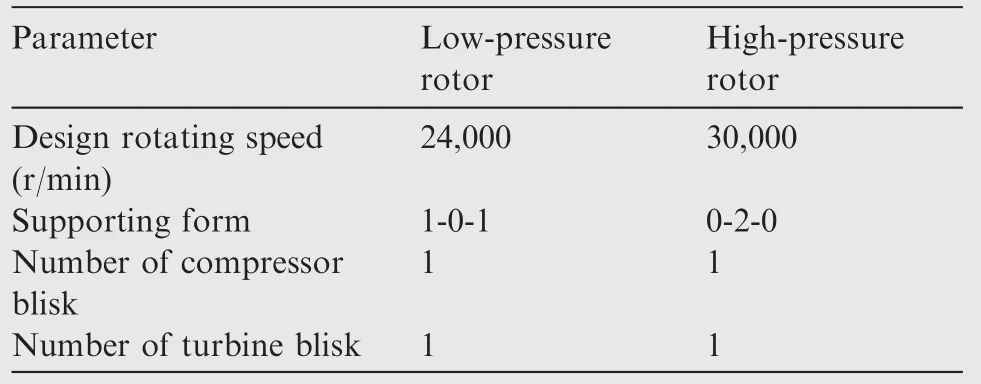
Table 1 Features of rotor systems.

Fig. 3 Finite element model of dual-rotor-support-casing coupling system.

5. Calculation of instantaneous structural intensity fields

The structural intensity field is a composite field composed of internal forces, moments, displacements and velocities. The existing finite element tools do not yet have the function of directly solving the structural intensity field. Therefore, based on Ansys Parametric Design Language (APDL), this paper has carried out secondary development of finite element program coupling with the powerful matrix computing ability of MATLAB language, and developed the simulation system of instantaneous structural intensity of aero-engines to calculate and visualize the structural intensity fields of the overall structure of aero-engines. The detailed calculation process of this simulation system is shown in Fig. 4.

This simulation system controls the data interaction and message passing between these two parts. The structure parameters,material properties,load and boundary conditions are input into the simulation system for finite element modelling of this coupling system and carrying out the transient forced vibration analysis. The computed results including translational and rotational displacements and velocities,internal forces and moments, and strain and kinetic energy are output to the file system ready to be read. Next, the simulation system pauses the calculation of the finite element tool and starts calling the in-house program. When these data are read in by the in-house program, they are first matrixed for subsequent calculations. The conversed coordinate system and these matrixed data are used for the calculation of instantaneous structural intensity fields. Finally, the computed results of structural intensity are read by the post-processing tool to visualize the instantaneous structural intensity fields.

The structural intensity fields can also be measured experimentally. At present, there are two main methods: contact measurements (accelerometers,25strain gauges26) and noncontact measurements (nearfield acoustical holography,27Laser Doppler vibrometer28).Due to the limited measurement principle and the complexity of the experimental devices, the current experimental measurements on the structural fields are limited to simple structures such as plates.The experimental data of structural intensity field or analytical solutions of rotor systems for aero-engines have not yet been found.Therefore,in this paper the modified modal superposition results of a simply supported plate presented in Ref. 22 are used to validate the accuracy of the results computed by this developed simulation system, which is given in detail in the Appendix C.

Fig. 4 Calculation flowchart of instantaneous structural intensity field.

6. Results and discussion

In the design process of the rotor systems, the application of the squeeze film dampers and the design requirements of rotor dynamics ensure that the rotors can smoothly pass its critical speeds during start-up and stop,29although the squeeze film dampers can not essentially attenuate the rotor vibration. In addition,since the aero-engine is mainly operated at its design rotating speeds,the designers pay more attention to the vibration and noise performances of the whole engine at these speeds to ensure the reliability and safety of the operation.30Therefore, this section analyzes the relationship between modal vibration characteristics and the vibrational energy flow transmission characteristics of the low-pressure rotor and the high-pressure rotor at their respective design rotating speeds.

The transient forced vibration calculation is carried out to this whole dual-rotor-support-casing coupling model to output the necessary date for the prediction of instantaneous structural intensity fields.The supports and casings as the transmission medium of forces couple the vibration of the low- and high-pressure rotors. Therefore, the vibrational energy flow transmitted from the vibration sources is not only transmitted on the respective rotor, but is also coupled to the vibration energy flow on the other rotor through the supports and the casings. These streams of vibrational energy flow respectively transmitted from low- and high-pressure rotors will interact with each other along the main transmission paths on the casing. Moreover, the vibrational energy flow from one rotor modal shape will couple with that from other rotor modal shape when the low- and high-pressure rotors are in different modal shapes. Therefore, the results of each rotor presented in the following sections have already taken the effects of the modal shape and the vibrational energy flow of the casings and the other rotor into consideration. In order to make the calculation result converge quickly and obtain more flow details of the vibration energy, a small-time step 0.0001 s is required to input to the calculation process, which is onetwentieth of the minimum rotor unbalanced force excitation period.The convergence analysis of this transient forced vibration calculation is detailed in Appendix D.

Fig. 5 Modal shapes of rotors (frame of rotor indicates undeformed rotor).

6.1. Modal shapes of the rotors

Due to the different structural dimensions, support stiffnesses and support patterns of the high-and low-pressure rotors,the predominant vibrational modal shapes at their respective design rotating speeds are also different.Therefore, the modal shapes and natural frequencies of the rotors have been expanded and extracted by rotor dynamics analysis taken the flexibility provided by the casing components and the rotating speeds into consideration. For the high-pressure rotor, the translational mode (cylindrical mode) at the frequency of 250.56 Hz dominates its main vibrational modal shape when operating at its design rotating speed, which is shown in Fig.5(a).For low-pressure rotor,the first-order bending mode at the frequency of 373.41 Hz dominates its main vibrational modal shape when operating at its design rotating speed,which is shown in Fig. 5 (b). The vibration deformation in the middle part of the rotor shaft is the largest. Compared to the translational mode, designers will pay more attention to the bending mode with more severe vibration conditions in the control of overall vibration for the aero-engines. The low-pressure rotor will experience more severe vibrations and will therefore receive special attention during the rotor dynamics design process. The phase of the unbalances forces also affects the predominant modal shape of the rotor. When the unbalanced force of the low-pressure compressor blisk is out of phase with that of the low-pressure turbine blisk,the conical whirling mode at the frequency of 149.92 Hz dominates the main vibrational modal shape of the rotor when it is operating at its design rotating speed,which is shown in Fig.5(c).In this kind of modal shape, the middle part of the rotor shaft is a conical stand point, where the vibration deformation is minimal, which is in absolutely contrast to the first-order bending modal shape.

Therefore, this section takes the middle part of the rotor shaft with large difference in modal vibration characteristics as the research object (as shown in Fig. 6), and analyzes the relationships between the modal vibration characteristics and the vibrational energy flow transmission characteristics of these three modal shapes mentioned above. For the lowpressure rotor, a small piece of tile-shaped segment with 220 elements is extracted from the middle part of the lowpressure rotor as a research object to avoid the errors caused by the volume integral results of the parameters of the area not interested in the calculation according to the Eq. (12), as shown in Fig. 6 (a). For the hollow high-pressure rotor, a full-circumference shaft segment with 480 elements is extracted as the research object to analyze the energy balance relationship of the full-circumference shaft segment of the rotor with the translational mode, as shown in Fig. 6 (b).

6.2. Energy relationships for different modal shapes of the rotor

6.2.1. The first order bending modal shape

When the rotor is in the first-order bending mode, the most deformed part appears in the middle of the rotor shaft, where the strain energy is the largest. Therefore, it is considered that there may be a transmission and conversion process between the vibrational energy flow and the mechanical energy there.This subsection calculates and analyzes the relationship between the instantaneous structural intensity and the rates of change of the strain energy and the kinetic energy of the research object shown in Fig.6(a)when the low-pressure rotor is in the first-order bending mode. The result is shown in Fig. 7.

Fig. 6 Segment located in the middle part of rotor shaft.

Fig. 7 Relationship between instantaneous structural intensity and rates of change of strain energy and kinetic energy for the first-order bending mode.

It can be seen from the result that compared with the kinetic energy, the segment with the largest deformation in the middle part of the first-order bending mode has more vibrational energy flow to participate in the transmission and conversion process to the strain energy, which is consistent with the previous consideration. It can also be seen from Fig. 7 that this segment not only absorbs the vibration energy but also releases the vibration energy recovered from the strain energy to the surrounding structures during the energy transmission and conversion process. Specifically, when the divergence of the structural intensity is negative, this segment absorbs the vibration energy and converts it into mechanical energy,most of which is converted into strain energy,resulting in a large deformation in the middle part of the rotor shaft.Conversely,when the divergence of the structural sound intensity is positive, this segment transmits vibration energy outward, and the strain energy stored in the previous stage is recovered. It can be seen that for the rotor in the first-order bending mode, there is a cyclically alternating transmission and conversion process between the vibrational energy flow and the strain energy in the middle part of the rotor shaft.In order to visually and intuitively display the transmission and conversion process between the vibrational energy flow and the strain energy shown in Fig. 7, the structural intensity divergence field, vector field and the strain energy distribution involved in the relationship in Fig. 7 are visualized at two moments, and the results are shown in Fig. 8.

As can be seen from Fig. 8 (a), at the time of 0.0001 s, the divergence of instantaneous structural intensity of the area A1is less than zero, which means that this area is absorbing the vibration energy at this time. From the diagram below it can also be seen that the streamlines of vibrational energy flow converge at this area.According to the previous analysis,most of this part of vibration energy converted into mechanical energy is stored at the area in the form of strain energy. As a result, as can be seen from Fig. 8 (b), at the time of 0.0002 s, the strain energy of this area is increased from the previous moment. Conversely, at the time of 0.0001 s, the divergence of structural intensity of area A2is greater than zero, and the strain energy stored at this area is recovered at this time and converted into vibrational energy flow releasing to the surrounding structures. From the diagram below of Fig. 8 (a) it can be seen that the streamlines of vibrational energy flow is diverging outwards from the area A2. As a result, the stored strain energy is decreased at the time of 0.0002 s.

6.2.2. The conical whirling modal shape

Fig.8 Vibrational energy flow transmission and conversion process of segment of rotor in the first-order bending mode(Diagram above:the strain energy; Diagram in between: the divergence of the instantaneous structural intensity; Diagram below: the streamline representation; Arrows: the structural intensity vectors).

Fig. 9 Relationship between instantaneous structural intensity and rates of change of strain energy and kinetic energy for conical whirling mode.

The vibration pattern of the conical whirling modal shape is exactly the opposite of that of the first-order bending modal shape,that is,the displacement and deformation in the middle part of the rotor shaft are minimal.Therefore,in order to analyze the differences in vibrational energy flow transmission characteristics of these two modal shapes, the research object for this kind of modal shape is still the segment shown in Fig. 6 (a). Based on the analysis of the previous subsection,it can be speculated that only a small part of the vibrational energy flow transmitted to the middle part of the rotor shaft is converted into mechanical energy, and most of it is dissipated by damping. Fig. 9 shows the relationships among the instantaneous structural intensity, the vibration energy dissipated by the damping and the rates of change of strain energy and kinetic energy.It can be seen from the result that the divergence of the structural intensity of the rotor shaft at the conical stand point is always negative, which means this segment always absorbs the vibration energy during the vibration period. Moreover, the magnitudes of the rates of change of the strain energy and the kinetic energy are extremely small, that is, the vibration energy absorbed at the conical stand point is hardly converted into the mechanical energy. Therefore, this part of the vibration energy is dissipated by the damping of this segment to maintain the energy balance.It can also be seen from the calculation result in Fig.9 that the trend of change of the dissipated vibration energy and that of the divergence of the instantaneous structural intensity are almost symmetrically distributed on the zero-value line, which means that the more vibration energy that is absorbed in this segment,the more it is dissipated by its damping, and these two change simultaneously. The calculation results shown in Fig. 9 verify the correctness of the speculation before the analysis in this subsection.

Fig.10 shows the strain energy distribution,the divergence and the streamline representation of instantaneous structural intensity of the segment of the rotor in this kind of modal shape. It can be seen from the in-between diagrams at these two moments shown in this figure that the divergence of structural intensity field in the area A3is less than zero,representing that the vibration energy is continuously absorbed by this segment.It can also be seen from the streamline representations at both of these two moments that the vibrational energy flow transmitted from the left and right sides of this segment converges in the area A3. However, it can be seen from the strain energy distribution diagrams that the magnitude and variation of the strain energy in the area A3are very small at these two moments, that is, the vibration energy absorbed in this area is not converted into the strain energy. As a result, the displacement and deformation in the middle part of the rotor with the conical whirling modal shape are very small. These visualization findings and results are consistent with the calculation results shown in Fig. 9.

6.2.3. The translational modal shape

As can be seen from Fig. 5 (a) and (b), compared with the first-order bending mode, the local deformation of the high-pressure rotor is small due to the overall translational displacement. Therefore, more attention should be paid to the vibration energy transmission characteristics of the fullcircumference shaft segment in this mode. This kind of segment is extracted as the research object in this subsection, as shown in Fig. 6 (b). Based on the Eq. (12), the energy balance relationship of this segment is calculated, and the result is shown in Fig.11.It can be found from the result that the maximum value of the divergence of structural intensity is less than zero, indicating that the segment absorbs the vibration energy during the overall vibration excitation period; in addition, the minimum value of the power done by the damping force is greater than zero,indicating that the damping of the structure performs a stable and positive damping characteristic, that is,the structure dissipates the vibration energy during the overall vibration excitation period. For the mechanical energy, it can be seen from Fig. 11 that most of the vibration energy converted into the mechanical energy is stored in this segment in the form of strain energy,which is the same as the mechanical energy conversion characteristic of the rotor in the first-order bending mode shown in Fig. 7. The main reason for this phenomenon is that the translational mode of the rotor will also performs a small amplitude bending deformation similar to the first-order bending mode, as shown in Fig. 5 (a). With the same material, this shorter and thicker hollow highpressure rotor has higher structural rigidity, so a small deformation will result in a large strain energy.

Fig.12 shows the transient distribution of the strain energy,the divergence of the instantaneous structural intensity, and the streamlines of the vibrational energy flow of this fullcircumference shaft segment at two adjacent moments.Locally, the vibrational energy flow converges at the area A4,and the divergence of the structural intensity is less than zero,and the strain energy increases. On the contrary, the divergence of the structural intensity of the area A5is greater than zero, and the stored strain energy is recovered and converted into vibration energy to be released outward, and the strain energy is decreased.This process is similar to the energy transmission and conversion process shown in Fig. 8. However, it can be seen from the strain energy distribution diagram of Fig. 12 that the distribution range of high-value strain energy is small, which has not formed a large distribution area as shown in Fig. 8. Therefore, the high-pressure rotor has less bending deformation and mainly performs a translational modal shape. For this full-circumference shaft segment, the vibrational energy flow is transmitted to this segment through the sections C1and C2shown in Fig.12(b).It is assumed that the vibration energy transmitted to the segment through the unit section at the unit time is a positive flux(+flux),as shown by the green dashed box in Fig. 12 (b); otherwise, it is a negative flux (-flux), as indicated by the yellow dashed box. The negative vibration energy flux is actually the structural intensity. According to the Eqs. (9) and (11), it can be easily found that the area integral of the flux through the total section of the segment is equal to the negative of the volume integral of the divergence of the structural intensity through this segment.From the result shown in Fig. 11, the total vibration energy flux through these two sections is always positive,which means that the vibration energy transmitted into the segment through these two sections is always greater than the vibration energy transmitted outward, and the increment of net vibration energy is greater than zero. Part of this net vibration energy is used to change the mechanical energy of this segment, and the rest is dissipated by the damping to maintain the energy balance.

Fig.10 Vibrational energy flow transmission and conversion process of segment of rotor in conical whirling mode(Diagram above:the strain energy;Diagram in between:the divergence of the instantaneous structural intensity;Diagram below:the streamline representation;Arrows: the structural intensity vectors).

Fig. 11 Relationship between instantaneous structural intensity and rates of change of strain energy and kinetic energy for translational mode.

6.3. Influence of grooving on the shaft on first-order bending vibration

From the above analysis,the vibration energy generated by the unbalanced forces of the blisk of the low-pressure compressor and turbine is converged in the middle of the rotor shaft, and part of this energy is converted into strain energy,which causes the first-order bending deformation of the rotor.Therefore, in the case of the same magnitude of unbalanced forces,the most direct way to reduce the bending deformation of the rotor is to prevent the vibration energy from being converged in the middle of the rotor shaft.There are two main methods to block the transmission of vibration energy on the shaft.One is the‘‘convex method”, that is, a circumferential stiffened ring is arranged on the shaft to block and dissipate the vibration energy; the other is the ‘‘concave method”, that is, the rotor is grooved on its shaft to reduce vibration energy flux by reducing the flow area of the vibrational energy flow and inducing the vibration energy vortices by the stepped shaft.Ma et al.31have been carried out related research on the influence of circumferential stiffened rings on vibration energy transmission characteristics. It was found that they can effectively block the transmission of vibration energy on the casing and attenuate the whole engine’s vibration. However, considering that the rotor is a rotating component of the aeroengine, especially for the low-pressure rotor of the dual-rotor engine,the gap between the high-and low-pressure shafts does not allow a higher circumferential stiffened ring located in the middle of the low-pressure shaft, so the ‘‘convex method” has a limited effect on suppressing the bending deformation of the rotor.

Fig. 12 Vibrational energy flow transmission and conversion process of segment of rotor in translational mode (Diagram upper left:strain energy; Diagram upper right: divergence of instantaneous structural intensity; Diagram below: streamline representation; Arrows:structural intensity vectors).

Fig. 13 Low-pressure rotor with circular grooves and its segments used for analysis.

Therefore, this subsection mainly studies the influence of the circular grooves on the bending deformation of the lowpressure rotor from the perspective of transmission control of vibrational energy flow, and compares the vibration energy and strain energy distribution in the middle of the rotor shafts with and without these grooves.Under the requirements of the torsional strength and shear strength, the low-pressure rotor after circumferential grooving is shown in Fig. 13. A circular groove is respectively opened at both ends of the middle part of the low-pressure rotor to block the vibrational energy flow from converging toward the middle part. The circular groove with width LG=0.02 m and outer diameter DG=0.03 m is shown in the segment I (L1=0.1 m) of this figure.

In order to ensure the comparability of the calculation results, the magnitude and phase of the unbalanced forces at the compressor and turbine blisk remain unchanged. Moreover, in order to evaluate the influence of these circular grooves on the characteristics of rotor dynamics, the modal analysis of the whole engine shown in Fig. 3 was carried out,and the natural frequency of the low-pressure rotor with the first-order bending deformation as the predominant mode is extracted.For the low-pressure rotor without circular grooves,that is 373.41 Hz,and for the rotor with circular grooves,that is 367.29 Hz. It can be seen that the change of the natural frequencies corresponding to the first-order bending mode of the low-pressure rotor before and after grooving is small. Therefore, the change of the vibration characteristics due to the change of the natural frequencies can be ignored, and the differences in calculation results between these two cases are mainly contributed to the influence of the circular grooves on the vibration energy transmission characteristics. In order to analyze the transmission characteristics of vibration energy flowing through the circular grooves, the structural intensity field of segment I at the moment of 0.0001 s is calculated and visualized, as shown in Fig. 14. Since the pattern of the structural intensity field of the segment I is similar at different times,but the circumferential position is different,this subsection takes the calculation result of the moment of 0.0001 s as an example. For ease of analysis, segment I is divided into three parts, M1, M2and M3, as shown in Fig. 14 (a).

Fig. 14 Streamline representation of instantaneous structural intensity field of segment I at the moment of 0.0001 s.

It is apparent from Fig. 14 that two pairs of oppositedirection vibration energy vortices V1and V2and V3and V4are induced on both sides of the circular groove. Fig. 14 (a)shows the top view (xoz-plane) of these vibration energy vortices, and Fig. 14 (b) shows the front view (yoz-plane) orthogonal to the view of Fig.14(a).As can be seen from Fig.14(b),these three-dimensional tornado-like vibration energy vortices are distributed in upstream of the interface between the subsegments M1and M2and downstream of the interface between the subsegments M2and M3. When the vibration energy generated by the unbalanced force of the compressor blisk is transmitted to the groove through the subsegment M1, the streamlines of vibration energy flow are continuously squeezed toward the shaft core due to the reduction of the flow area,so that the intensity of vibration energy of the shaft core is increased, and that near the outer wall of the subsegment M1is decreased, thereby generating an energy difference in the radial direction. Since the vibration energy is always transmitted from a high value to a low value, the vibration energy is transmitted toward the outer wall of the subsegment M1from the shaft core near the interface between the subsegments M1and M2. And then blocked by the outer wall, the vibrational energy flow is transmitted in the -z direction to form the reverse flow.Finally,it merges into the mainstream and is continuously squeezed into the shaft core forming vibration energy vortices V1and V2.These two induced vibration energy vortices will continuously squeeze the mainstream of vibrational energy flow to the shaft core,which forms positive feedback. The vibration energy transmitted from the shaft core of subsegment M1to the subsegment M2is directly transmitted to the outer wall of the subsegment M2,and this vibration energy is blocked by the outer wall of this subsegment. A portion is drawn into the vibration energy vortices V1and V2, which is transmitted back to the subsegment M1again; the other portion is transmitted from the outer wall of the subsegment M2to the M3.At this time,the vibration energy of the core of subsegment M3is low,the vibration energy,therefore,is transmitted from the outer wall to the core in this subsegment.Consistent with the previous analysis, the vibration energy vortices V3and V4are induced in the subsegment M3. Different from the vortex pairs V1and V2,these two vortices V3and V4are adjacent,and no mainstream of vibrational energy flow transmits between them.Therefore,the vortex pairs V3and V4can be regarded as the vibration energy recirculation zone generated at the downstream of the interface when the vibration energy is transmitted from the subsegment section M2to M3,as shown by the dotted box in Fig.14(a).Therefore,the vibrational energy is transmitted from the subsegment M1through M2to M3mainly along the paths indicated by the yellow dotted line in Fig.14(a),and two vibration energy vortices V1and V3(or V2and V4)are distributed on both sides of these paths.These two vortices shunt a part of the vibration energy transmitted along these paths, and some of the shunted vibration energy is held inside the vortices, and is dissipated by the damping of the structure occupied by themselves. Thereby the vibration energy transmitted from the subsegment M3to its adjacent downstream shaft segment is decreased. In order to analyze the dissipation effect of the vibration energy vortices,the structural intensity distribution of the Slice 1 containing the vortex core lines of the V1and V2is shown in Fig. 15,o′:the centre of Slice 1;a′and b′:the positions of outer ring of V2at line lv; c′: the position of vortex core of V2at line lv.

Fig. 15 Distribution of instantaneous structural intensity of Slice 1 and that along diameter indicating x-axis.

Fig. 17 Distribution of strain energy.

Table 2 The maximum and average values of vibration energy and strain energy of the segment II for the low-pressure rotor with and without grooving.

The vortex core lines (dotted curves) of the vortices V1and V2and the profiles of outer ring of those vortices can be clearly seen from Fig. 15. A part of the recirculating vibration energy transmitted along the -z direction is transmitted to the mainstream along the outer ring profiles of the vortices and squeezed into the shaft core to continue the transmission in the+z direction again,and the other portion is drawn into these vibration energy vortices. In order to analyze the variation trend of the vibration energy that is drawn into the vortices V1and V2, the structural intensity distribution along the diameter in the x direction (the white dotted line lv) is extracted, as shown by the curve in Fig. 15. It can be seen that the curve is symmetrically distributed with the line of x=0 (the center of Slice1). Therefore, this subsection only takes the vibration energy vortex V2as the analysis object.The intersection points of the outer ring profiles of the vortex V2in the Slice1 and the line lvis a and b,respectively, and the intersection point of the line lvand the vortex core line is c.These intersection points correspond to a′, b′and c′in the curve. It is apparent from the radial (a to b) distribution of the structural intensity in the vortex V2that the vibration energy at the position c’ where the vortex core is located is the lowest. Since the vibrational energy flow that is drawn into the vibration energy vortex is continuously spirally transmitted from the outer ring to the vortex core, the vibration energy transmitted along the structural intensity streamline is decreased, that is, part of the vibration energy held by the vortices is continuously dissipated by the structure occupied by those vortices. It can be seen from the above analysis that the vibration energy vortices V1-V4induced by the circumferential grooves on the rotor shaft shunts and dissipates part of the vibration energy transmitted from the subsegment M1to M3, which reduces the vibration energy transmitted by the subsegment M3to its adjacent downstream shaft segment.In order to verify the correctness of the above findings, the segment II (L2=0.1 m) adjacent to the subsegment M3is extracted as the research object, which is located in the middle of the rotor shaft with the largest bending deformation, as shown in Fig.13.The vibration energy distribution and strain energy distribution of the segment II for the low-pressure rotors with and without circular grooves are compared respectively, the results are shown in Figs. 16 and 17. It can be seen from the results shown in these two figures that the vibration energy and strain energy of segment II of the rotor after grooving are significantly decreased. The specific data is listed in Table 2. Therefore, it can be demonstrated that the vibration energy vortices induced by the circumferential groove upstream of the vibrational energy flow can shunt and dissipate part of the vibration energy transmitted to the middle of the rotor shaft, thereby effectively reducing the first-order bending deformation of the rotor.

7. Conclusions

In this paper, the structural intensity method was applied to study intrinsic physical relationships between rotor modal shapes and instantaneous vibrational energy flow transmission characteristics. Firstly, the vibration energy balance relationship was derived from the general equation of motion to associate structural intensity with structural vibration characteristics.And then a dual-rotor-support-casing coupling model with rotor unbalanced forces was established by finite element method. Numerical examples including this physical relationship for rotors with the first-order bending mode, the conical whirling mode and the translational mode were carried out by the developed simulation system. Streamline representations were applied to visualize structural intensity fields to show the sources, sinks and transmission paths of vibrational energy flow. Finally, the influence of grooving on the rotor shaft on first-order bending vibration was studied to attenuate this kind of harmful vibration. The conclusions of this paper can be summarized as follows:

(1) The volume integral of the divergence of the structural intensity at any time is equal to the negative of the sum of the rate of change of mechanical energy and the damping dissipated energy.That is,part of the vibration energy transmitted to structure is converted into strain energy and kinetic energy, and the other part is dissipated by the damping of the structure. Similarly,the stored mechanical energy can also be recovered and released to the surrounding structures in the form of vibration energy.

(2) When the unbalanced force of the low-pressure compressor blisk is in phase with that of the low-pressure turbine blisk, the vibration of the rotor is dominated by the first-order bending mode. The transmission and conversion processes of vibrational energy flow and the storage and release processes of strain energy alternately occurs in the middle part of the rotor, resulting in a large bending deformation at this area. When these two unbalanced forces of the low-pressure rotor are out of phase,the predominant modal shape is change to the conical whirling mode. In that case, most of the vibration energy is dissipated by the damping in the middle part of the rotor shaft, and is not converted into strain energy and kinetic energy, so the displacement and deformation are small at this area, forming the conical stand point. As for rotors with the translational mode,it has partial vibration energy transmission characteristics of the rotor in those two modes mentioned above.One is that part of the absorbed vibration energy is converted into strain energy, but because of its limited distribution range, it does not cause obvious bending deformation of the rotor;the other is that the net vibration energy of the middle part of the shaft is always greater than zero, that is, the vibration energy is always absorbed at this area.

(3) In order to attenuate the first-order bending vibration of the rotor, the vibration energy generated by the unbalanced forces of the compressor and the turbine blisk should be prevented from converging to the middle part of the shaft as much as possible under the design requirements of rotor dynamics, such as grooving on the rotor shaft to induce the vibration energy vortices to shunt and dissipate a portion of the vibration energy which is going to be transmitted to the middle part of the shaft. As for the rotor with the conical whirling modal shape,the rotor component is suggested to be processed by a light-weight and high-damping material to enhance the damping dissipation of the vibration energy and attenuate the conical whirling vibration at the compressor and the turbine blisk.

Acknowledgements

This work has been supported by the National Key Technology Research and Development Program of China (No.2016YFB0901402) and the Major Program of National Natural Science Foundation of China (No. 51790513).

Appendix A. The structure parameters of the dual-rotor-sup port-casing coupling system are listed in Table A1.

Appendix B. The material properties of the dual-rotor-sup port-casing coupling system are listed in Table A2.

?

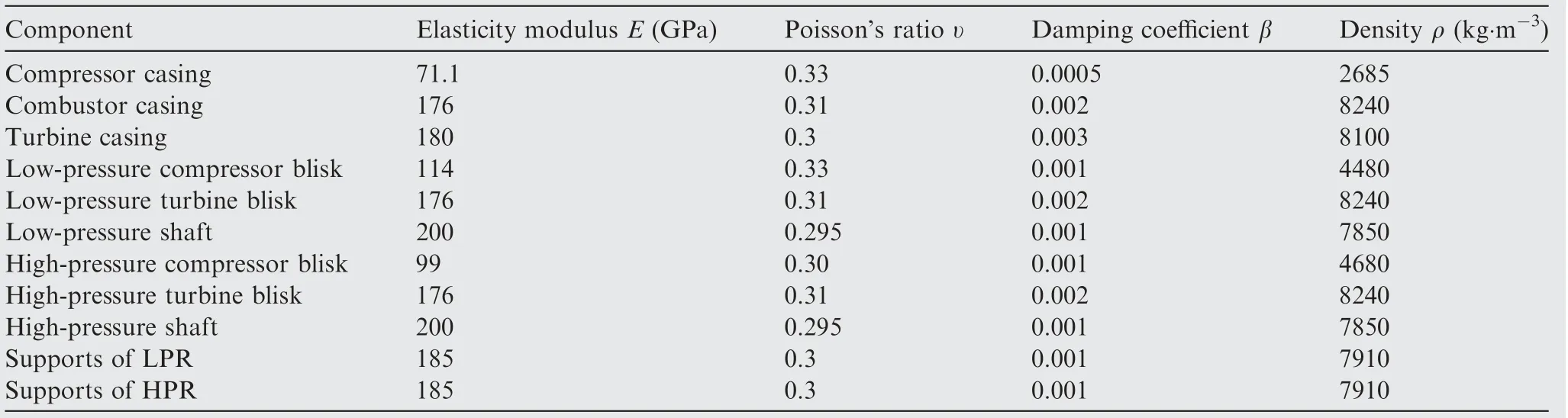
Table A2 Material properties.

Table A3 Material properties of the plate.22

Table A4 Parameters of external force and viscous damper.22

Appendix C. Base on Ref. 22, the finite element model of a simply supported rectangular plate with 3.0 m long,1.7 m wide and 0.01 m thick was established by the developed simulation system. The material properties of this plate are listed in Table A3.The parameters of the external force and the viscous damper are listed in Table A4. The forced vibration analysis was carried out by the finite element tool, and the matrixing process of output results and the calculation of the structural intensity fields of this plate were performed by the in-house program.Fig.A1 shows the computed result by this developed simulation system and the modified modal superposition result presented in Ref. 22. Comparing these two results, it can be seen that the positions of the external force and the viscous damper and the transmission paths of the vibration energy are very consistent, which verifies the accuracy and reliability of the computed results by the developed simulation system.

Appendix D. The Time-Average Velocities (TAVs) is used for assessing the convergence of the transient forced vibration calculation shown in Fig. A2. The TAV can be expressed as:

The TAVs in the x-, y-, and z-directions are extracted for three key nodes which are taken at the coupling nodes between the components for transmitting vibration loads and vibration energy between components. The details of these nodes are as follows:

● Node 1:One of the coupling nodes between the casing and the supports.

Fig. A1 Structural intensity fields of a simply supported plate.

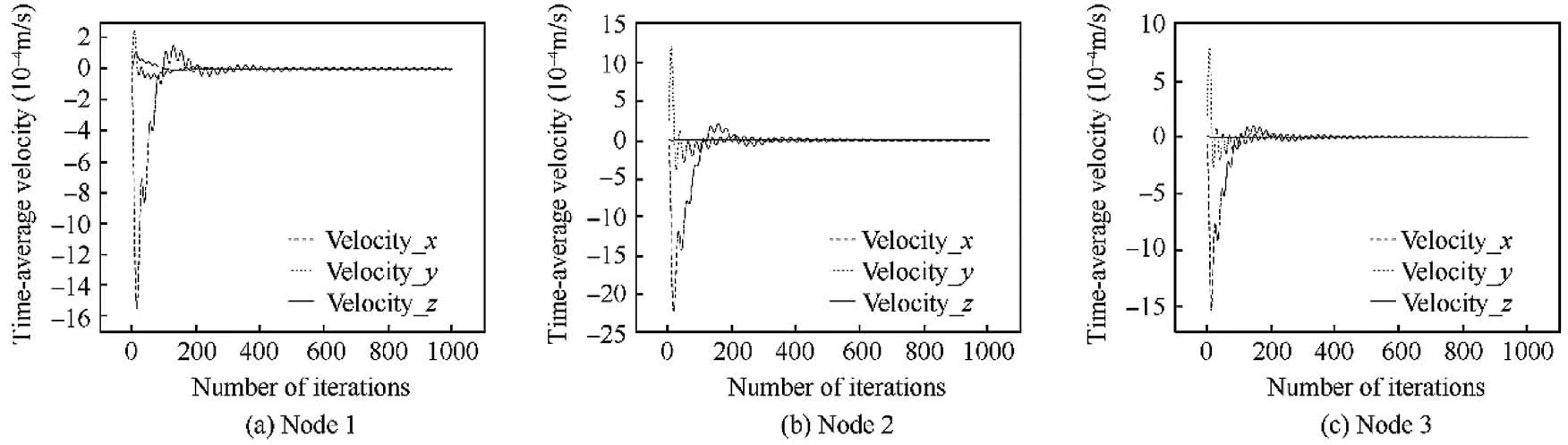
Fig. A2 TAV-NI curves of three monitored nodes in the x-, y-, and z-directions.

● Node 2: One of the coupling nodes between the LPR and the bearings.

● Node 3:One of the coupling nodes between the HPR and the bearings.

The TAV-NI curves of these three nodes in the x-,y-,and zdirections are shown in Fig.A2.It can be seen from the results that the TAVs of these three nodes in the x-, y-, and zdirections tend to zero as the NI increases, which means these nodes are already in a stable periodic response.Especially,the transient responses have been well converged when the NI is greater than 600. Therefore, the transient response data used for calculating instantaneous VEF in this study was extracted from the results of iteration steps from 980th to 1000th,which are in a period of vibration excitation.