Topology optimization in lightweight design of a 3D-printed flapping-wing micro aerial vehicle
2020-02-24LongCHENYnliZHANGZuyongCHENJunXUJinghoWu
Long CHEN, Ynli ZHANG, Zuyong CHEN, Jun XU,b, Jingho Wu,*
a School of Transportation Science and Engineering, Beihang University, Beijing 100083, China
b Advanced Vehicle Research Center (AVRC), Beihang University, Beijing 100083, China
KEYWORDS 3D printing;Finite element analysis;Flapping-wing micro aerial vehicle;Topology optimization;Transmission system
Abstract Topology optimization is an effective method to obtain a lightweight structure that meets the requirements of structural strength. Whether the optimization results meet the actual needs mainly depends on the accuracy of the material properties and the boundary conditions,especially for a tiny Flapping-wing Micro Aerial Vehicle(FMAV)transmission system manufactured by 3D printing. In this paper, experimental and numerical computation efforts were undertaken to gain a reliable topology optimization method for the bottom of the transmission system. First,the constitutive behavior of the ultraviolet (UV) curable resin used in fabrication was evaluated.Second,a numerical computation model describing further verified via experiments.Topology optimization modeling considering nonlinear factors,e.g.contact,friction and collision,was presented,and the optimization results were verified by both dynamic simulation and experiments. Finally,detailed discussions on different load cases and constraints were presented to clarify their effect on the optimization. Our methods and results presented in this paper may shed light on the lightweight design of a FMAV.
1. Introduction
Flapping-wing Micro Aerial Vehicle(FMAV)is a new type of aircraft that mimics the flying behavior of small birds or insects.1,2Stimulated by the development of 3D printing technology,numerous studies on the design of linkage-based transmission systems for a FMAV have been conducted by scientists and engineers.3-8One of the major objectives during the design procedure is to reduce the weight of the transmission system as much as possible, i.e. the lightweight design,without any structural failure. A lighter transmission system can extend the endurance of a FMAV within the limits of on-board power but is more likely to dissatisfy the structural strength requirement. Including FMAVs, the lightweight design of aeronautics structures is of vital importance to their performance and has been extensively studied recently.9-11
To balance the weight reduction and the satisfaction of structural strength requirements, topology optimization has been widely employed during the lightweight design.The Solid Isotropic Material with Penalization (SIMP) method is one of the most popular methods in topology optimizations and has been extensive developed.12-15Rietz16and Martinez17discussed the theoretical convergence properties of the solid isotropic material with penalization (SIMP) method, and Sigmund18reported the advantages of a modified SIMP method, which includes a minimum stiffness that is independent of penalization. Siva et al.19demonstrated the feasibility of the SIMP method in optimizing the additive manufacturing through the FEA solver package Altair OptiStruct. Choi et al.20compared the structural optimization performance of three commercial software, i.e. Genesis, MSC Nastran, and OptiStruct, by solving various representative examples via SIMP method, and they concluded that OptiStruct provided the optimum solutions. Stanford et al.21-23carried out the topology optimization of a flapping wing (including the wing root compliant mechanism)via a nonlinear dynamic finite element model,with a full couple of elastic,inertial,aerodynamic,and actuator forces.The research of Stanford et al.provides a valuable reference for applying topology optimization to the lightweight design of FMAV. Given the broad implication of topology optimization in the design of various structures,however, less experience is provided in the topology optimization of a tiny 3D-printed FMAV transmission system, especially with the consideration of dynamic aerodynamic loads. The contact, friction,and collision in the FMAV transmission system, which is highly random and sporadic during operation,challenges the reliability of the topology optimization. Thus,the topology optimization and structural integrity assessment of a 3D-printed FMAV transmission system under dynamic aerodynamic loads are investigated.
In this paper,a numerical model describing the mechanical behavior of a 3D-printed FMAV transmission system was established and verified. The topology optimization modeling considering the nonlinear properties, e.g. contact, friction and collision, was then presented, and the optimization was focused on the bottom of the transmission system,which occupied a large portion of the total weight.Details for the research procedure are presented in Fig. 1. First, the material constitutive and aerodynamic loads acting, as an input of the Finite Element (FE) analysis for the transmission system, are determined via experiments. Three FE models, i.e. the flexible FE model with a 1D revolute rivet, the solid FE model with 1D revolute rivet and the flexible FE model with solid rivet are developed for different analyses. The motion output of the flexible FE model with solid rivet is compared with the observation of actual transmission system, which is to validate the method for the FE dynamic analysis. The dynamics analysis of both solid and flexible FE models with 1D revolute are conducted to make clear the effect of flexibility.The bottom component of both solid and flexible FE models with 1D revolute are further input into the topology optimization and the corresponding optimized structures are obtained. A FE dynamics analysis of both optimized structures are carried out and the effects of load cases and displacement constraint on the optimization are then discussed.
2. Problem definition
As shown in Fig.2(a),the FMAV transmission system consists of a pair of two-stage gear systems, a bottom, and two symmetrically arranged four-bar linkages. All components of the transmission system are 3D-printed using UV curable resin except for the gears(0.5 modulus),which are made of standard engineering plastic. The components are connected by aluminum or copper rivets and a snapshot of the 3D-printed assembly is shown in Fig. 2(b).
The aerodynamic loads of the wings, as an input of the dynamic simulation and topology optimization of the bottom,is measured by experiments(Fig.3).A force sensor is mounted on the optical breadboard to measure the lift generation of the FMAV, while the flapping frequency is measured by a fiber optic probe.
Our objective is to reduce the weight of the components which occupy a larger portion of the total weight of the transmission system while ensuring the structural strength for reliable wing kinematics. Given a certain lift generation of the FMAV,a weight reduction can improve flight maneuverability and endurance. The bottom shown in Fig. 2(a) accounts for 49.36% of the total weight of the transmission system and is thus selected as the focus of our topology optimization. The difficulties of the weight reduction of the bottom via topology optimization are mainly resulted from following aspects: the selection of a feasible topology optimization algorithm and the setup of the optimization including the modeling of bottom and accurate input of aerodynamic loading.

Fig. 1 Overlook of research procedure.

Fig. 2 FMAV transmission system.

Fig. 3 Experimental platform to measure the lift generation of a FMAV.
3. Methodology and modeling
3.1. Material constitutive
As most components of the transmission system are fabricated via 3D printing using UV curable resin, the material constitutive of the resin was first measured via uniaxial tensile tests.The specimens were 3D-printed using the UV curable resin according to the ASTM standard D638-14,and the tensile test was conducted by INSTRON 8801.The loading speed was set at 2 mm/min and Fig.4 presents the experimental stress-strain curves of three individual tests, which shows a good agreement.The constitutive behavior shows that the stress increases nonlinearly with the strain until the peak stress.Thereafter,the plastic deformation occurs until the specimen breaks down at the failure strain.
The Ramberg-Osgood model is employed in our study to describe the nonlinear elastic section,24,25and a Mazars damage model is used to describe the plastic softening section.26,27The Ramberg-Osgood model is presented by the following equation,

where E is the elastic modulus,ε is the strain and σ is the stress.Ckand u are the intensity coefficient and the strain hardening coefficient,respectively,which are related to the material hardening degree. The Eq. (8) can be further transformed into

where σ0denotes the yield strength.
Marincek proposed that the elastic limit strength can be determined by a half elastic slope line.28In this case,the elastic modulus E of the elastic section was estimated at 2.06 GPa according to the initial slope of the tensile stress-strain curve.A half elastic slope line is constructed in the tensile stressstrain curve, as shown in Fig. 5(a), and the elastic limit point locates at (0.04713, 49.0004 MPa), i.e. the value of σ0is 49.0004 MPa. The values of α and u are then determined as α=4.1643 and u=0.6991 by a curve fitting of data points according to Eq. (9).
The plastic softening section is described by Mazars’ damage model,26

Fig. 4 Stress-strain curves of three 3D-printed specimens.

where ω is the damage equation, ε0is the strain value corresponding to the starting point of the softening section. The coefficients A and B are estimated by a curve fitting of data points within the plastic softening section of the stress-strain curve:A=0.26364 and B=35.31666.A comparison between experimental results and data-fitted constitutive model is given in Fig. 5(b) and a reasonable agreement is achieved.
3.2. Modeling of aerodynamic forces
To conduct the dynamic simulation and topology optimization accurately, an appropriate estimation of aerodynamic forces generated by the wing is necessary.The aerodynamic loads distributed on the wing surface is further expressed by a combination of forces and torques(six-axis in total)loaded at the wing root (Fig.6),where FLand FDrepresent the lift and drag. MLand MDare the equivalent aerodynamic moment,respectively.Using the experimental platform described in Section 2, the real-time lift generation is measured at a flapping frequency of 30 Hz (the lift generation at this frequency is enough for the FMAV to take-off), as shown in Fig. 7(a). Note that the noise in the lift measurement is mainly caused by the mechanical vibration of the transmission system and the effect of inertia of the flapping wings. Lee et al.29presented an improved quasi-steady aerodynamic model for flapping wings, which was validated to be feasible over a wide range of Reynolds number and wing geometries. According to the quasi-steady aerodynamic model, the lift and drag generated by the wing are as follows:

where ρaand S are air density and wing area. CLand CDare lift coefficient and drag coefficient,respectively.Uref,the reference velocity, is defined as follows:

where f is the flapping frequency, R2is the second moment of wing area,c is the chord,and R is the wingspan.In our study,the wing geometry and kinematics are defined as R=85 mm,c=28 mm, f=30 Hz and φ=130°. An example of the lift and drag estimated by the quasi-steady model is shown in Fig. 7(b), where T denotes the period of a flapping cycle,T=33.33 ms. The mean lift predicted by the model is 0.313 N,which is only 4.03%deviated from experimental measurements.This suggests that the quasi-steady model is feasible to estimate the aerodynamic loads on the flapping wing.Moreover, the lift and drag are assumed to locate at the R2and the aerodynamic forces and torques at the wing root are thus calculated (Fig. 7(c)).
3.3. The multi-body dynamics model

Fig. 5 Numerical fitting of stress-strain curves by constitutive models.

Fig. 6 Illustration of boundary conditions. ol-xlylzl and or-xryrzr are adjoint coordinate systems set on the rocker. The constraints and loads of the FE model are labeled in the sketch.

Fig. 7 Real-time forces (at 30 Hz) measured by force sensor and estimated by quasi-steady aerodynamic model.
In general, there are two numerical models used in our study,i.e.the multi-body dynamics model,which is employed to simulate the dynamic behaviors of the FMAV transmission system and the topology optimization model of the bottom, which is introduced for its lightweight design based on different boundary conditions. The FE model of the transmission system is developed using Altair HyperWork 17.0.The solid 164 element is selected to model the 3D-printed components and the plastic gears. The leading-edge of the wing is simplified by a uniform beam to include the effect of inertia.The total amount of solid finite elements is 46,083.
The rivets that act as a shaft between components are modeled by two kinds of elements, i.e. solid element and 1D revolute element. The solid modeling takes full account of the assembly gap between parts (Fig. 8(a)), and thus reflects the collision and friction of the parts. As a result of this, the FE model with solid rivet is used to evaluate the structural integrity of the FMAV transmission system.The 1D revolute modeling of the rivets is employed to calculate the load transfer between components by an integration of the resultant force of all nodes on each rivet wall. Thus, the FE model with 1D revolute rivets is used to calculate the loading input for the topology optimization of the bottom, as shown in Fig. 8(b).Note that the solid modeling of the rivets cannot realize the load transfer between components.
To explore the influence of flexibility on the dynamics of the transmission system, we construct a flexible model and a rigid model, respectively. In the rigid model, all components are defined as rigid bodies, with no consideration of deformation,vibration, and contact behaviors. In the flexible model, except for the gears and rivets, all other components of the transmission system are fabricated via 3D printing using UV curable resin.The constitutive behavior of UV curable resin is defined using the *MAT_PIECEWISE_LINEAR_PLASTICITY material model in LSDYNA R72 The pre-defined parameters are as follows: E=2.06 GPa, ρ=1.16 g/mm3, Poisson ratio ν=0.35, yield stress σ0=49.1 MPa, shear modulus Es=80 MPa and the effective stress-strain curve. The effective stress σeffgets start from the first point of real yield stress,and the real strain εTcorresponding to the yield stress value is taken as the zero point of effective strain εeff. Other values of effective strain are obtained based on the data-fitted model in the plastic softening section, calculated by:

Fig. 8 Finite element model of the FAMV transmission system.

To avoid any stress concentration caused by gear meshing,the flexible deformation of gears and rivets is neglected. The material properties of gears, rivets, and motors are defined by the *MAT_RIGID model, the values of which are listed in Table 1.
For the flexible model of the transmission system, the friction and collision would appear on the surface of each component during operation. Furthermore, the stiffness of contact surfaces is not the same. In this paper, the contact model*Contact_Automatic_Single_Surface in LSDYNA R7.0 is used to define the contact relationships of components. The whole FE model is defined as a contact set.27The coefficient of static friction is defined at 0.2, and the coefficient of dynamic friction is defined at 0.15. In order to control the hourglass energy and the penetration depth of the model, the following parameters are defined: SFS, SOFT, SBOPT, and DEPTH. SFS (Scale factor on default slave penalty stiffness)is the scale factor of the total penalty stiffness of the FE model,which equals to 2.SBOPT is the definition of the contact algorithm based on the element section,which equals to 4 underlying a sliding contact. DEPTH is used to define the measured depth for surface penetration,which equals 23,indicating that the surface penetration is measured at both nodes and edges.
3.4. The topology optimization model
Considering the weight reduction margin, the bottom of the transmission system is selected for topology optimization. To ensure the assembly relationship, the sidewalls of each hole are set as a non-design zone, and the rest parts are set as the design zone.The FE model of the bottom has been established in Section 3.3 and a mesh with 9809 elements is selected according to a validation on the mesh density. The topology optimization design is carried out using Altair OptiStruct 17.030(Fig. 9(a)), which was based on the variable density method. The variable density method divides a continuous structure into finite elements and sets the density of each element as the design variable. The value of relative density of each element(xp)is defined within[0,1],and the topology optimization of the bottom is transformed into the optimal distribution of material, which can be expressed as

where ρ1is the initial density of each element, and ρ is the material density after topology optimization. The element is an entity and should be retained when xp=1, while the element is an empty hole and should be removed when xp=0.For cases in which the relative density is within [0,1],an interpolation function is introduced to calculate the correspondingYoung’s modulus E. In other words, a relationship is established between xpand E, where the SIMP method is usually used. The SIMP method is formulated as follows:
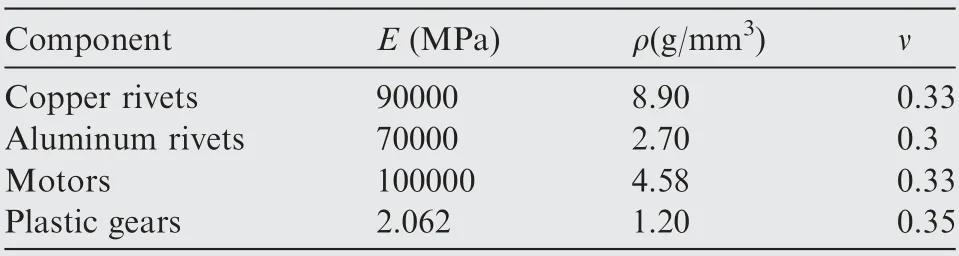
Table 1 Material properties of selected components in transmission system.

Table 2 Procedure of topology optimization.

where Ei,E0and Eminrepresent the interpolated Young’s modulus of element i,the initial Young’s modulus of element i and the Young’s modulus of an empty hole. N is the number of finite elements, and p is the penalty factor. During the topology optimization, the total volume of the bottom is defined as the objective function and the constraints are set in von Mises stress and static displacement. Thus, the objective function of the topology optimization based on the variable density method is expressed as follows:
Minimize

where X is the vector of design variables, V* is the total volume of the bottom, Viis the volume of element i and N is the number of elements.
The optimization of the objective function is subject to following constraints:
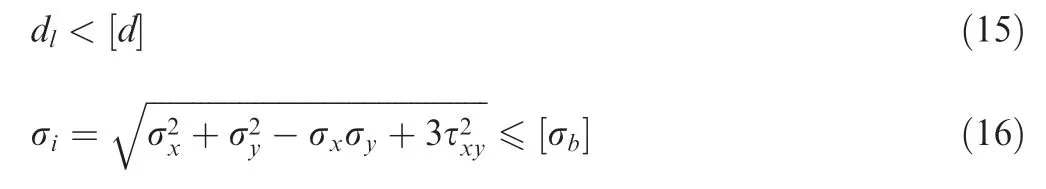
where dlis the static displacement of specified nodes in the zdirection and [d] is the limits of this displacement, which is±0.6 mm.Note that the displacement is measured at the node that is the farthest from the motor mounting of bottom. σiis the Von Mises stress of element i and σb[ ] is the strength limit of the material,which is set at 40 MPa.The calculation of σiis related to the stress in×and y direction (σxand σy) and the shear stress τxy. Moreover, to ensure the smoothness of the mounting surface,the draft direction is fixed along the normal direction to the upper surface of the bottom. In order to meet the minimum geometric size requirement of the 3D printing,the local minimum size of the topology optimization model is set to 0.8 mm.
The procedure of topology optimization is described in Table 2. A gradient-based optimization method, i.e. the local approximation method,is employed by the OptiStruct to solve the optimization problem. This method is a reformulation of the ‘‘Method of Moving Asymptotes (MMA)” since the move limits of the design variable are used to control the convergence. The MMA leads to a convex optimization problem and the update of the structure between iterations is done by solving the MMA approximate problem, which is based on the sensitivity analysis, i.e. the calculation of gradients of the objective function and constraint functions w.r.t the design variables. The ‘‘Lagrangian Duality” method is used to solve the MMA approximation in Step 5.
The topology optimization of the bottom is conducted based on both rigid and flexible models and the loads(the forces and torques shown in Fig. 9(b)) at the rivet holes within a flapping cycle are obtained via dynamic simulations of the corresponding models. Here, the load cases based on the flexible model are obtained when the Von Mises stress is larger than 20 MPa (The threshold of 20 MPa corresponds to appropriate load cases at an acceptable cost of optimization time). The load cases based on the rigid model are obtained when the max z-direction force(FR,max) is achieved, as the stress distribution is not resolved in the rigid model.
4. Results
4.1. Movement description of the transmission system
The motions of the FMAV under the frequency of 30 Hz are recorded by a high-speed camera. While flapping, the linking rods are influenced by the inertia, centrifugal forces, and aerodynamic forces, which might intensify the gaps between rivets and holes, leading to an increase in flapping amplitude.

Fig. 9 Topology optimization model of bottom.
Fig. 10(a) shows the motion of the transmission system within one cycle (33.3 ms). Note that the case with no wingmounted is also provided here. The flapping amplitude of the flexible model with solid rivets is consistent with the observation of experiments. As shown in Fig. 10(b) the flapping amplitude increases by about 10° due to the installation of wings.According to the simulation of the FE model,the increment of flapping amplitude is 13° (Fig. 10(c)). Therefore, the setup of dynamic simulation based on the FE model is further verified.
4.2. Structural strength description of the transmission system
Based on the material characterization of UV resin, the strength limit is used as a failure criterion to assess the structural integrity of the transmission system. We analyze the dynamic simulation results of the flexible model with solid rivets and obtain the σvondistribution of each component at the critical state within two flapping cycles(Fig.11).It is obvious that the σvon,maxof each component is lower than the tensile strength limit of the UV resin (49 MPa), which meets the structural strength requirement. The σvon,maxof the bottom is 25.9 MPa,which occurs around the rivet holes due to the stress concentration phenomenon. The observation that the maximum Von Mises stress of the bottom is far below the tensile strength limit indicates that there is enough margin for topology optimization.
As shown in Fig. 12, the force and deformation in the vertical (z) direction of the rigid and flexible FE models are compared. For the rigid model, the force in the z-direction at the rivet hole is far less than that of the flexible model. Once the transmission system is rigid, the vertical force at rivet holes of the bottom is transferred from the aerodynamic forces.However,the 3D-printed bottom is a flexible body with deformations and the bending will inevitably aggravate the load in the vertical direction. This indicates that the flexible model can better characterize the bending of the bottom due to the flexibility of the UV resin.

Fig. 10 Flapping angle comparison between experiments and dynamic simulations of the FE model.

Fig. 11 Maximum Von Mises stress of the components of the transmission system. From left to right, rods, rockers, and bottom.

Fig. 12 Comparison of dynamic simulations based on rigid and flexible models.
4.3. Topology optimization of the bottom component
The distribution of material density coefficient of the optimized bottom based on the rigid and flexible model is shown in Figs.13(a)and(b),respectively.Here,a larger material density coefficient corresponds to a higher stress and need to be consolidated. The optimization results based on the two models are obviously different.The optimized bottom based on the flexible model is more compact than its counterpart based on the rigid model. The ratios of weight reduction based on rigid and flexible models are 46.9% and 40.2%, respectively, when the elements with material density coefficient greater than 0.5 are considered.Further static analysis of the two models is performed and the maximum von Mises stresses of both models are less than 49 MPa, as shown in Figs. 13(a) and (b). Hence,the optimized bottoms meet the structural strength requirement.
4.4. Strength verification of the optimized bottom component
In Section 5.3, we evaluate the structural strength of the optimized bottom based on the static stress under the state of the optimized load transfer path. The material properties defined in the topology optimization is isotropic, which excludes the anisotropy of additive manufacturing and the collision,friction, and coupling deformation of the bottom. Therefore,the dynamic simulation is carried out to verify the structural integrity of the optimized bottom in this section.
Note that the surface of the optimized bottom has subtle roughness due to the difference in mesh size. It is thus a creative process to adjust the optimized bottom artificially to make it more in line with the requirements of re-meshing and 3D-printing manufacture. Starting with the original bottom, the redundant material is removed along the edge of the material distribution shown in Fig. 14 and the optimized bottom is obtained. Then, the original bottom is replaced by the optimized one during dynamic simulations. The boundary conditions are the same as those in Section 4.1.4.
The comparison of deformation in the z-direction is shown in Fig. 14(a). The simulation results of both rigid and flexible models are presented here.The optimized bottom based on the rigid model generates larger vibration and bending than its counterpart based on the flexible model. The σvon,maxof the optimized bottom based on the rigid model and the flexible model are 39.51 MPa and 29.88 MPa (Fig. 14(b)). The σvon,maxof the optimized bottom based on the rigid model is located around the rivet hole for the installation of secondgrade gears, which bears large shear stress due to bending.However, the rigid model cannot obtain accurate z-direction loads caused by the nonlinear factors of the material.This further confirms that the load cases of topology optimization based on the rigid model cannot reflect the actual status and results in larger shear stress.The flexible model takes the effect of structural deformation on the load into consideration.

Fig.13 Topology optimization results of the bottom.Note that the elements with material density coefficient above 0.5 are shown here.

Fig. 14 Dynamic simulation of transmission system with the optimized bottom.
5. Discussion
5.1. Effect of load cases on optimization
In this section, we compare the influence of four criterions in load case selection on the optimization results, i.e., the maximum resultant force state (FR,max), the maximum deformation state (Dz,max), σvon,max, and the multi-states of abovementioned three factors. Based on the dynamic simulations at 30 Hz, the moments when the resultant force at the rivet holes is above 120 N are chosen as representatives(Fig.15(a)).The moments with deformation in z-direction above 0.2 mm are chosen, as shown in Fig. 15(b). The topology optimizations with load cases defined according to FR,maxand Dz,maxare then performed. The multi-states principle selects the moments that meet the requirements of FR,max,Dz,max,and σvon,max.The distribution of Von Mises stress of all load cases chosen based on different criterions within two flapping circles is shown in Fig. 15(c).
Topology optimization results based on four different criterions in load case selection are shown in Fig. 16(a). The load transfer path and the ratio of weight reduction both vary with the change of criteria. The optimization bottom based on FR,maxis similar to that based on σvon,maxand multi-states.The ratio of weight reduction for the multi-states-based case is lowest among all four cases. The load transfer path of the case based on Dz,maxhas a larger distribution area than others.Compared to the original bottom, the material distribution area of the optimized bottom based on Dz,maxis retained as far as possible to disperse the shear force generated by vibrations in the z-direction. The optimized bottoms are shown in Fig. 16(b).
The original bottom is thus replaced by optimized bottoms and the dynamic simulations are then conducted to further verify the optimized bottom. The boundary conditions are the same as those in Section 4.1.4.The σvondistribution of different bottoms is shown in Fig. 17(a). The σvon,maxof all optimized bottoms is larger than that of the original bottom,while is less than the tensile strength limit of the UV resin.Moreover,the σvon,maxprediction also varies with different optimized bottoms. The σvon,maxof the FR,max-based optimized bottom is the lowest. The stress value of the Dz,max-based optimized bottom is more distributed,which indicates that a larger coverage area can better reduce the bending to resist shear failure.Fig.17(b)shows the edge deformation in z-direction of different bottoms within two flapping cycles. The deformation of the multi-states-based optimized bottom is smaller than others.As more factors are considered in topology optimization for the multi-states case, more materials will be retained to enhance the ability to resist deformation. The σvon,max-based optimized bottom has the largest ratio in weight reduction.A detailed comparison of optimized bottoms is given in Table 3.

Fig. 15 Different load cases of bottom.

Fig. 16 Topology optimizations of bottom based on different criterions in load case selection.
In summary, different criterions in load case selection have their own goals during the topology optimization. Selecting load cases based on σvon,maxand FR,maxcan achieve a higher weight reduction while ensuring the requirement of structural strength. Selecting load cases based on Dz,maxcan result in an optimized bottom with a larger distribution area, which can better disperse shear stress and improve the ability to resist bending.
5.2. Effect of the displacement constraint
As shown in Fig.17(b),the vibration in the z-direction of optimized bottoms is larger than that for the original bottom.This might aggravate the vibration of transmission mechanism,resulting in unstable aerodynamic performance of the flapping wings.In this section,parameter configuration of the displacement response function is adjusted to further constrain the zdirection deformation in the topology optimizations.

Fig. 17 Dynamic simulations of different bottoms.

Table 3 Comparison of optimized bottoms.
The topology optimization in Section 4 and Section 5.1 are based on the static displacement constraint, which is set at±0.6 mm. According to the z-displacement of the original bottom shown in Fig. 17, where the max deformation in the z-direction is 0.38 mm, the constraint of static displacement is reduced to±0.4 mm in this section.Other settings in topology optimization are the same as those introduced in Section 4.2, and the load cases in this section are defined based on σvon,max.
The topology optimization result of the bottom after an adjustment of static displacement constraint is shown in Fig. 18(a). Unlike the four models in Section 6.1, the load transfer path between the farthest rivet holes and the middle rivet holes is wider given the adjustment of static displacement constraint.The static stress distribution of optimized bottom is shown in Fig. 18(b), and the maximum static stress meets the requirement of structural strength. The optimization model,with a weight reduction of 37.3%, is outlined by the material density coefficient in Fig. 18(c).
The σvon,maxof the optimized bottom is 26.03 MPa, which meets the requirement of structural strength (Fig. 19(a)). The Dz,maxof the bottom is 0.46 mm, which is slightly higher than the original bottom (0.38 mm) and exceeds the constraint of the displacement response function, as shown in Fig. 19(b).The maximum Von Mises stress appears around the rivet holes for the big gear. The elements in this region exhibit an excessive deformation, therefore a block is added to consolidate the structure.
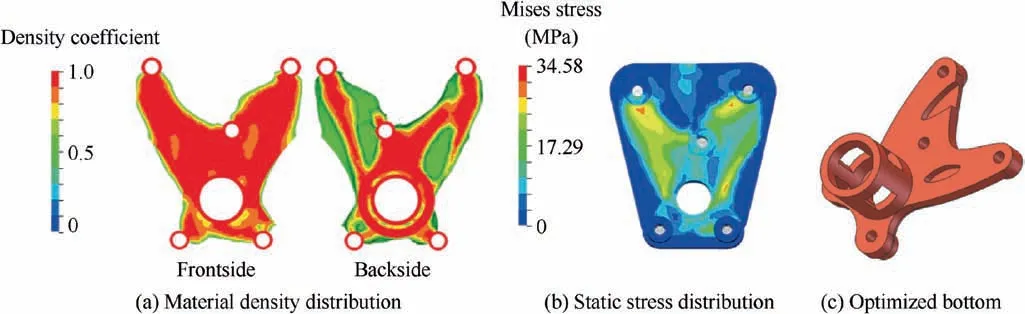
Fig. 18 Topology optimization results with an adjustment of static displacement constraint.

Fig. 19 Dynamic simulation result of the optimized bottom with displacement response.

Fig. 20 Dynamic simulation results of the optimized bottom with consolidated block.
The optimized bottom with a consolidated block is shown in Fig. 20(a), and the weight is reduced by 38.84% compared to the original one. In order to control the total weight of the bottom, the area with low material density, as shown in Fig. 19(a), is artificially removed, thus compensate the weight increase due to the consolidated block. A dynamic simulation is carried out for the final design of the bottom and the maximum von Mises stress state is shown in Fig. 20(b). The σvon,maxis 26.4 MPa, which meets the requirements of structural strength and is lower than that of any other optimized bottom.The Dz,maxof the optimized bottom with consolidated block is 0.372 mm,which is lower than that of the original bottom (0.38 mm). Therefore, an appropriate static displacement constraint in the topology optimization of the transmission system can effectively improve the ability to resist deformation energy.
6. Conclusions
This paper presents the modeling method, reliability evaluation, and the topology optimization design of an 3D-printed FMAV transmission system. The findings of this article are helpful for the lightweight design of an FMAV, and the key findings are summarized as follows:
(1) A dynamic simulation modeling method based on the constitutive model of UV curable resin and nonlinear dynamic characteristics of the transmission system is presented,which is used to assess the structural integrity of the transmission system and obtain the load case for topology optimization.
(2) A dynamic simulation method used to verify optimized results considering nonlinear factors, e.g. contact, friction and collision, is introduced, which compensates the inadequacies of the static method.
(3) Selecting load cases based on the σvon,maxor FR,maxcan increase weight reduction and improve computational efficiency, compared to multi-states.
(4) Selecting load cases based on the Dz,maxallows an improved ability to resist bending and the optimized bottom has a larger coverage area.
(5) A proper displacement constraint based on the stiffness analysis of the original bottom can effectively improve the performance of the optimized bottom.
Acknowledgement
This research was primarily supported by the National Natural Science Foundation of China (No. 11672022).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Design and experimental study of a new flapping wing rotor micro aerial vehicle
- CFD/CSD-based flutter prediction method for experimental models in a transonic wind tunnel with porous wall
- Prediction of pilot workload in helicopter landing after one engine failure
- Study of riblet drag reduction for an infinite span wing with different sweep angles
- Modulation of driving signals in flow control over an airfoil with synthetic jet
- Strong interactions of incident shock wave with boundary layer along compression corner
