Transient flow characteristics and performance of a solid rocket motor with a pintle valve

Anchen SONG, Ningfei WANG, Junwei LI, Baoyin MA, Xinjian CHEN

School of Aerospace, Beijing Institute of Technology, Beijing 100081, China

KEYWORDS Numerical simulation;Pintle motor;Shock wave;Solid propellant rocket;Variable thrust

Abstract The pintle valve is currently the most promising technology among all thrust control methods for solid rocket motors. Pintle structure and working condition play a critical role in the successful operation of a pintle motor. Here, 2D transient simulations of a pintle motor using dynamic meshing are performed. Reynolds-averaged Navier-Stokes equations are solved with the implementation of an RNG k-ε turbulence model.In cold flow test,emphasis is placed on the effect of pintle structure,and in hot flow test,emphasis is placed on the effect of propellant pressure exponent. Validation is performed first by comparing the present results with available cold-test experimental data. This shows that the transient simulations can provide good predictions for pintle motors with a relative error of less than 2%in terms of the chamber pressure.It can be found that,when the gas supply system is different, the working principles and conditions of pintle motors are different. The feedback process in propellant combustion has a significant impact on its operation and the effect on the pintle motor performance of different pintle structures is achieved by different variations in the equivalent throat area.Finally,the pressure exponent is an important parameter in hot flow test and changes of thrust in hot flow test are not monotonic, because changes in the flow field and motor performance are asynchronous.

1. Introduction

Solid Rocket Motors (SRMs) are widely used in aerospace engineering due to their various advantages, i.e., simplicity,reliability, and good storage performance;1however, there are many unsolved problems in traditional SRM, such as reignition and thrust control. In general, thrust is an important performance parameter for an SRM,2but the fixed grain shape and nozzle size mean that the thrust of an SRM cannot be changed in operation.3There has been renewed interest in thrust control and regulation to overcome this inherent weakness in solid propulsion systems.

There are many measures available to achieve variable and programmable thrust of SRMs, such as the fluidic nozzle throat method,4single-chamber dual-thrust method,5and pintle valve method.6The pintle valve method is an easy way to regulate the thrust. A pintle valve is similar to a globe valve in which the cross-sectional area of the flow passage is changed by a plug.7The pintle changes the chamber pressure and thrust by changing the nozzle throat area with a fixed propellant grain. This method can regulate thrust continuously over a wide range. Besides, quick response and mission flexibility can be realised using this method.8Therefore,the use of pintle valves has been widely studied in SRM research and development.

Nomenclature

A Area

AbBurning surface area

a Magnification of n

b Magnification of a

c Specific heat

d Diameter

FNThrust of motor

FPForce on the pintle

f Frequency

k Thrust regulation ratio

M Molar mass

n Pressure exponent

P Pressure

R Gas constant

r0Radius of nozzle

T Temperature

Subscripts

C Combustion chamber

e Nozzle exit

in Inlet

initial Initial value of a parameter

k Thrust regulation ratio

Max Maximum

Min Minimum

Superscript

— Averaged value

t Time

ttrgtTime to reach a target value

tmovTime when the pintle stops

u Gas velocity

V Volume

vPPintle velocity

L Length of movement

α Convergent half angle

β Half-angle expansion

ε Expansion ratio

θ Angle of pintle profile

μ Propellant burning rate

μdViscosity

ρ Gas density

ρpDensity of propellant

σ Basic error

τ Response time

pintle Pintle main body

stable Stable value of a parameter

stem Pintle stem

t.eq Equivalent throat

throat Nozzle throat

V Cavity

W Nozzle wall

The first application of a pintle valve in an SRM was accomplished by Aerojet Corporation in the 1960s; however,its application in actual operational systems was not achieved.9Rapid development of pintle motors was achieved in the 1990s,and pintle motors were widely used in Attitude Control System(ACS)10,11and ejector seats.12The pressure exponent of the propellant is an important influence factor for SRM with a pintle valve. Different from traditional SRM, the chamber pressure in SRM with a pintle valve changes simultaneously with the pintle movements. If the pintle is positioned at some intermediate position, the chamber pressure is dependent on burning properties of the propellant. For example, pressure exponent of the solid propellant greatly affects burning rate of the propellant at different operating pressure of the motor.This problem has been well introduced in Refs. 13,14 However, the previous studies are mostly made based on experimental results. It is difficult and costly to change the pressure exponent and then obtain variation of motor performance with pressure exponent.The data obtained in the experiment is also limited. In recent years, Alliant Techsystems Inc.(ATK)have designed a new pintle structure with a plurality of radial bleed passageways, which can balance the load.15The use of pintle valve is helpful to increase the range, speed,and maneuverability of traditional SRMs. It is also the most effective method of controllable thrust propulsion in SRM for the continuous control and higher thrust regulation ratio.Therefore, it is valuable to study the further improved performance of SRM with a pintle valve in theory and engineering.Experimental research is costly and it is often difficult to observe the details of flow field. Thus Computational Fluid Dynamics (CFD) simulations were used to study pintle motor flow fields.3,16

With the development of computer technology, CFD has been widely used in studies on flow fields in nozzles,17,18SRMs,19-21and valves.22,23There have been many reports dealing with optimisation of pintle motors through simulated and experimental methods. Theoretical analyses were undertaken in Ref. 24-27 to find that the thrust produced during pintle motion depends upon the throat area with respect to the pintle shape and size; however, most simulations are conducted based on steady state conditions,so the effects of transient flow are omitted. Dynamic flow fields of different pintle shapes were numerically investigated in Ref. 6,9. It was found that the dominant factor which determines thrust is chamber pressure rather than pintle shape. Therefore, it was concluded that the force on the pintle is more important than thrust in a pintle structure. The dynamic characteristics of a pintle nozzle were analysed in Ref.28,29 using a sliding mesh.It was found that the thrust coefficient determines the effects of nozzle flow separation on overall performance.Three turbulence models in numerical simulations were compared in Ref. 30. It is found that there is a deviation of approximately 2% in the temperature distributions, although the thrusts are similar in all models. Thrusts at different pintle locations were predicted in Ref.31 using one-dimensional nozzle theory: a quasi-linear relationship is found between the thrust and valve pintle position.Cold test, hot test, and numerical simulation were performed in Ref. 4,32 to obtain relationships among the effective throat-area ratio, thrust-adjustment ratio, and modified mass-flow-rate ratio. It is found that the rules of mass-flowrate ratio in cold flow test and hot flow test are different, so a modified engineering formula is proposed for use in hot test when the motor is designed based only on steady cold-test results.

It can be concluded that pintle motors in previous studies are mainly used in traditional pintle structures; however, as shown in Ref.15, there are some new pintle structures now in use. There is little research on transient flow field in pintle-controlled nozzles working in other pintle structures.Besides this,previous studies are conducted either in cold tests or in hot tests: There are few comparisons between these two conditions.In fact,gas inlets in different tests affect the working performance. In hot test, solid propellant is burned in the combustor. Chamber pressure affects the propellant burning rate, which is absent in a cold test.

The objective of this work is to analyse the pintle valve technology used in SRMs.The characteristics of pintle motors are analysed, and then cold tests are conducted to verify the CFD conclusions. The effects of different pintle structures and pressure exponents are numerically investigated with a view to increasing the thrust-control performance.

2. Experimental set-up and simulation method

2.1. Experimental set-up

To verify the simulation method,the pintle motor is subjected to a cold flow test. The experimental set-up consists of a gas supply system, pintle-driving system, Data AcQuisition(DAQ)system,and an SRM with a pintle(Fig.1).Parameters used in cold flow tests are listed in Table 1.

The pintle-driving system is used to control and drive the pintle.The pintle valve is driven by an electromagnet.By powering the electromagnet through the power supply, an electromagnetic force is generated to control the movement of the pintle. The duration for which, and frequency at which, the electromagnet is powered, are controlled by computer, and then the switching frequency of the pintle is controlled. When the electromagnet is energised,the pintle is moved by the electromagnetic force to the nozzle, and the nozzle throat area is reduced. When the power is turned off, the pintle moves back to the combustor under the spring force,and the nozzle throat area is increased. The pintle can move in one-way or reciprocating modes.

In the pintle motor, the pintle is placed coaxially along the nozzle.The angle between the inlet gas direction and the pintle axis is 90°. In cold test, high-pressure air bottles are used to supply high-pressure gas into the combustor and nozzle. By varying the pintle position inside the nozzle, the air mass flow rate is changed dynamically.Accordingly,the thrust generated by the nozzle is changed.In hot test,propellant burning rate is an important factor affecting thrust regulation. Solid propellant is placed in the combustor, and the flow valve upstream of the combustor is closed. Solid propellant is ignited, hightemperature gas flows from the combustor into the nozzle,and the thrust is then regulated by moving the pintle. Movement of the pintle changes the nozzle throat area,thus increasing (or decreasing) the chamber pressure. Consequently, the magnitude of the thrust changes.33Hot tests are not undertaken in this study, and only simulations of hot tests are conducted.

2.2. Numerical simulation methods

2.2.1. Governing equations

Reynolds-averaged Navier-Stokes (RANS) simulation is an economical and widely used numerical method for SRM problems. Its capability of providing rapid and good predictions has been proved. Therefore, RANS simulations are employed in this study to solve the mass, momentum, and energy equations in pintle motors. In this study, two-dimensional (2D)axisymmetric geometries are used. As chemical reactions are neglected,these equations can be written in the following conservative forms34:

where E=e+0.5uiuj, e is total specific energy

The governing equations are supplemented with the equation of state for ideal gas

The numerical work is conducted based on the commercial CFD code FLUENT®, which has been successfully used for applications related to SRM. It is applied to solve the timedependent Navier-Stokes equations with backward first-order time discretisation. Previous research30has found that the thrusts of the pintle motor are similar in simulations using Spalart-Allmaras, RNG k-ε, or k-ω SST turbulence models.Therefore, considering calculation time and accuracy, an RNG k-ε model is used here.

2.2.2. Dynamic mesh conditions

Since the flow area changes during pintle movement, a fixed mesh cannot be used and a dynamic mesh is required. In dynamic mesh conditions, the calculation area is changed.Therefore, the control volume V changes in the flow field.The conservation equations can be expressed in integral form as35

Fig. 1 Schematic of experimental set-up and rocket motor with pintle.

where t is time,V is the control volume,ρ is gas density,∂V is the boundary of the control volume, u is the gas velocity vector, ugis the velocity of the dynamic mesh boundary, A is the area vector of the control volume, Γ is diffusion factor,and SΦis the source term of Φ.

To update the mesh in deforming zones subject to motion defined at the boundaries,smoothing and remeshing were conducted.Smoothing is a method of adjusting a zone with a moving or deforming boundary. The interior nodes of the mesh move, but the number of nodes and their connectivity remain unchanged. Remeshing can agglomerate cells that violate the skewness or size criteria.It can also locally remesh the agglomerated cells or faces. If the new cells or faces satisfy the skewness criterion, the mesh is locally updated with the new cells.Otherwise, the old cells are retained.

The moving method of the dynamic mesh is controlled through the profile. Using a profile, both the direction and the velocity value are given. The moving method of the pintle(reciprocating or one-way) can also be determined. In experiment, the pintle is controlled by electromagnet. Therefore,although the frequency of the pintle movement can be obtained, the specific movement method of the pintle is difficult to obtain. Considering that the macroscopic characteristics of SRM with a pintle valve is the focus of this study, the pintle is considered to be at a constant velocity during the pintle movement. It can be calculated as

Where vPis the pintle velocity.

2.2.3. Working characteristics of a solid pintle motor

As shown in Fig. 2, different from solid motors with a fixed nozzle,thrust regulation of the pintle motor is mainly achieved by changing the nozzle throat area. When the pintle moves along the axis, the minimum venting area of the nozzle is no longer the Laval nozzle throat. It is the annular area between the pintle and the nozzle wall. This area changes with pintle positions and a calculation method is established to find the relationship between the minimum venting areas and the pintle positions.

Table 1 Parameters used in cold flow tests.

Different from other valves operating at subsonic speeds,the annular area is not always the effective area. Fig. 2 shows that the minimum area between the nozzle throat and the pintle is defined as equivalent throat area(At.eq)(the nozzle profile and the pintle profile are discretised into several points to calculate this). The annular areas formed by the discrete points along the nozzle and the pintle are calculated separately. The minimum result among them is At.eqat that place, which can be calculated as

where At.eqis the equivalent throat area, Ai,jrepresents the annular areas between the point i on the pintle and the point j on the nozzle, and Athroatis the area of the nozzle throat.

Coordinates are established to compare pintle positions and the performance of the pintle motor. The position where X=0 is the contact position of the pintle with the nozzle,and L is the length of pintle movement. When L is less than 5.4 mm, At.eqdoes not change and is 80.15 mm2. The reason for this is that the nozzle throat area is the smallest area in this stage. As for the stage L=5.4 mm to L=9 mm, At.eqdecreases in a quasi-linear manner and the minimum At.eqis 5.81 mm2at L=9 mm. The minimum area is constantly changing, and the pintle movement at this stage can regulate the performance of the motor.

Furthermore, thrust is an important parameter that can evince the performance of an SRM. It can be calculated theoretically when the gas in the motor is deemed to form a one-dimensional isentropic flow. Two forces are important to any study of the performance of a pintle motor: the thrust of the motor (FN), and the force on the pintle (FP)(Fig. 2).

As for a pintle motor,there is flow separation therein while the pintle is close to closure because of the small equivalent throat area; however, the flow can still be regarded as onedimensional isentropic flow, because the pressure difference between the inside and outside of the motor is very large,and flow separation has little effect on thrust coefficient. The thrust of the pintle motor can be calculated as36

where ρ is the gas density,ueis the velocity,A is the cell area,r0denotes the radius of the nozzle,P is the pressure in the nozzle,and Pais the ambient pressure.

Pintle motors are used in thrust regulation,so it is necessary to kNow their performance in this regard. The thrust regulation ratio can be calculated as

where kmaxis the maximum thrust regulation ratio, FN,maxis the highest transient thrust, and FN,minis the lowest transient thrust.

Fig. 2 Schematic of pintle movement and variation of At.eq with pintle position.

The force on the pintle is also an important parameter and can be calculated by integrating the pressure on the nozzle wall as follows (related parameters are shown in Fig. 2):

where FPrepresents force on the pintle, Ppintleis pressure on the pintle, r is the radius of the position on the pintle, and θ is the angle of the position on the pintle.

Response performance is another focus of research on pintle motors. Response time is used to compare the time lag between the moment when the parameter reaches a target value and the moment when pintle finishes moving. It can be calculated as

where τ is the response time,ttrgtis the time for a given parameter to reach its target value,and tmovis the time when the pintle finishes moving. The response time of different parameters is indicated by a subscript,e.g.,τP,τm,and τFare the response times of pressure,mass flow rate,and force,respectively;ttrgtis the time taken for the parameter to become stable during pintle movement in one-way operation, while it is the time taken for the parameter to reach the nearest extreme value in reciprocating operation.

2.3. Computational domain and boundary conditions

The simulations are performed with a 2D axisymmetric,density-based, implicit, unsteady solver. The governing equations are discretised using the second-order upwind scheme in spatial terms and the first-order implicit scheme in temporal terms. The gradients are computed using the Green-Gauss node-based method. The flux type is an AUSM algorithm to enforce conservation.For better accuracy,the time step in this transient simulation is set to 1×10-5s, and the time resolution of the simulation results is 5×10-4s.

The computational domain with boundary conditions is illustrated in Fig. 3(a), and a schematic of the dynamic mesh settings in this study is shown in Fig. 3(b). The whole length of possible pintle movement is 9 mm.When L is changed from 0 to 9 mm, the equivalent throat area changes from 80.15 to 5.81 mm2. Detailed schematics (0 mm, 1.8 mm, 3.6 mm,5.4 mm, 7.2 mm, and 9.0 mm) during movement are shown.The number of elements in the grid during the whole range of pintle movement is 50000 to 78000, and the maximum cell skewness during the whole movement is less than 0.71. Grid quality meets transient simulation requirements. Grids near the pintle are refined to simulate greater change in flow thereat.The pintle stem and the moving axis are treated as deforming parts.Deformations occur along their axes based on their positions. Other parts remain stationary.

Three pintle designs are assessed here (Fig. 4). The Standard Design (SD) is shown in Fig. 4(a), which has the advantages of low processing difficulty and a relatively mature technology. The Drainage Design (DD) (Fig. 4(b)) is based on the published work,15and the diameter of the passageway is 0.1 mm. It is a load-balanced improvement over the SD which can effectively reduce the pressure drag. The Plug Design (PD) (Fig. 4(c)) is based upon a choked nozzle. This design can reduce the influence of back pressure and has a higher linearity of regulation.

Two kinds of gas are used: compressed cold air is used in Section 3.1 and 3.2,and hot gases arising from propellant combustion are used in Sections 3.3.Gas in the motor is considered to be an ideal gas and is compressible.The density is calculated by using the ideal gas equation of state.The viscosity is calculated by using the Sutherland equation, and because the gas is considered to be single component,the molar mass and specific heat are constant. Gas parameters used in these simulations are listed in Table 2,where T is the temperature,P is the pressure, and R is the gas constant.

The outlet boundary condition is set to a pressure outlet.The nozzle wall, combustor wall, and pintle wall are assumed to be adiabatic.The inlet boundary conditions used in cold test are different from those considering propellant combustion.In a cold test,it is set to a pressure boundary at the inlet.In a hot test, the combustor pressure affects the propellant burning rate, so the inlet is set to a mass flux inlet. The burning rate of the solid propellant is based on Vieille’s law.19

It can be found that burning rate can be particularly sensitive to the value of the pressure exponent.Therefore,the mass flux inlet can be analysed by

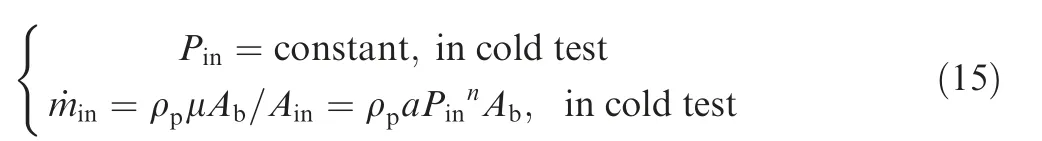
where Pinis the inlet pressure, ˙minis the inlet flow rate, Abis the area of the burning surface of one grain, ρpis the density of the propellant, μ represents the burning rate of the propellant,and subscripts a and n identify the burning rate coefficient and pressure index, respectively.

2.4. Mesh independence analysis

In the process of numerical calculation, a moderate mesh size is beneficial to save the computing time and obtain a relative accurate result. Three different computational meshes (coarse mesh: 28698 grids, medium mesh: 37065 grids, fine mesh:52334 grids) are employed to calculate the same case as listed in Table 1,including steady condition and transient condition.At first,using three meshes,the steady flow condition is firstly calculated to obtain the same initial condition for the dynamic simulations. Fig. 5 shows variation of the chamber pressure and thrust with mesh number at the steady flow condition.The maximum differences for the chamber pressure and thrust are not larger than 0.02%.Accordingly,it is demonstrated that the results for all the mesh are independent of the mesh size in the steady flow field.

From the above analysis,it can be concluded that the initial conditions for transient calculations are grid-independent.Then simulations of the dynamic flow fields using three meshes are carried out. For three meshes, their boundary conditions,dynamic mesh settings and pintle moving methods are all the same. As depicted in Fig. 6, the variation of pressure and thrust with time during the pintle movement for the three cases are almost the same. It shows that the calculated results are independent of the grid when mesh is moving. Therefore, the fine mesh (mesh number 52334) is used in this study.

Fig. 3 Boundary conditions and dynamic mesh settings in simulation.

Fig. 4 Schematic of pintle structures.

3. Results and discussion

3.1. Validation of simulation method with a cold test

To validate the simulation method,both cold tests and simulations of a pintle motor in SD form are conducted(Fig.1),and the parameters for cold test are listed in Table 1.In cold tests,high-pressure air at 6 MPa enters the motor from the inlet,and the pintle moves in reciprocating mode. The frequency of this back-and-forth motion is 14 Hz, over a distance of 9 mm at a pintle velocity of 0.25 m/s (implying pintle travel time from L=0 to L=9 mm of 0.0357 s).

The pressure in the combustor, cavity, and pintle head are extracted from two monitoring points with coordinates (mm)of PC,PVof(-35,25),(-35,11)as shown in Fig.2.The measured PCis compared with the simulated value (Fig. 7). It is found that the simulated PCvalue matches that from the cold test.The maximum PCin the cold test is 7.57 MPa,and that in the simulation is 7.64 MPa. The difference in their maximum values is less than 0.1 MPa,so their relative errors are less than2%. The amplitude of oscillation PCin the cold test is 1.20 MPa,and is 1.25 MPa in the simulation.Besides,the measured frequency in the test is 14.00 Hz,and the calculated oscillating frequency is 14.01 Hz. Therefore, the simulation could be deemed reasonable.

Table 2 Gas parameters used in simulations.

Fig. 5 Chamber pressure and thrust for different meshes in steady flow condition.

Fig.6 Chamber pressure and thrust during pintle movement for different meshes.

Fig.7 Comparison between measured and simulated pressure in a cold flow test.

Fig. 8(a) shows typical Mach number contours during a round of movement, and the effect of the pintle movement on the flow field is discussed. It can be found that, when the pintle starts moving at t=0 ms as shown in ①, At,eqis 80.15 mm2and this is the maximum equivalent nozzle area.The flow field is smooth, and there is an oblique shock wave.When L=5.4 mm as shown in ②, At,eqbegins to decrease.The gas near the pintle head is compressed,and a compression wave can be seen therein.Then At,eqgradually decreases as the pintle moves forward(e.g.,57.33 mm2in ③and 36.19 mm2in④), and PCgradually increases from 7.00 MPa in ③ to 7.24 MPa in ④. Besides, strong shock waves appear in ③and ④. A shock wave attaches to the pintle surface in ③,and a new shock wave is formed near the nozzle divergent section. As for ④, the strength of the shock wave increases towards the downstream divergent section, and then it strikes the wall and produces new strong shock waves. At L=9.0 mm in ⑤,the pintle is the closest to the nozzle throat.At,eqis only 5.81 mm2(its minimum value).The oblique shock wave and reflection shock wave become the strongest. It is observed in ⑤that the nozzle fluid is divided into two parts by the reflection shock wave. The centre is the main flow, a high-speed flow area; the outside is the secondary flow, a low-speed flow area. The Mach number in the main flow is higher than the secondary flow at the same axial position.Then because the motor is working in reciprocating mode,the pintle stops moving forward and starts moving backward.At first, At,eqchanges as the pintle moves. It is observed that,although At,eqis the same, PCis 7.57 MPa in ⑥, some 0.33 MPa higher than in ④, because the rate of decrease of PCis slower than the rate of increase of At,eq,and during backward movement, pintle motion shock waves persist and are stronger than those in ③and ④. When the pintle moves to⑧, there is a strong shock wave in the nozzle, while there is only a weak compression wave in ②. Finally, it reverts to its initial position (L=0 mm), and the flow field becomes smooth again.It can be concluded that the change of the flow field has a lag to the pintle movement, which is more obvious during the backward process. This leads to a potential significant difference in the flow field between the moving forward and backward process, even though the pintle positions are the same.There is a significant flow separation when the pintle valve is close to the nozzle wall.The flow velocity in the center main flow is higher than that in the surrounding secondary flow.

Fig. 8 Transient flow field and pressure change during pintle movement.

Fig. 8(b) shows the performance of the pintle motor when the pintle moves forward from L=0 mm to L=9 mm and then back to L=0 mm. During this movement, PCincreases from 6.33 MPa to 7.64 MPa within 38 ms, and then decreases to 6.40 MPa at 71.5 ms; FNdecreases from 3.23 to 0.74 kN within 37.5 ms, and then increases to 3.40 kN at 66.5 ms; FPdecreases from 1.19 kN to -0.43 kN within 37.5 ms, and then increases to 1.10 kN at 72.5 ms. The maximum thrust regulation ratio (kmax) is 4.59, and the maximum FNis found at L=8.38 mm, where At,eq=18.56 mm2; however, the minimum At,eqis 5.81 mm2at L=9 mm. Differing from a Laval nozzle, the change in FNis inconsistent with the change in At,eq. This is due to the hysteresis of the flow relative to the change in At,eq. Besides, when L=6.71 mm and At,eq=57.33 mm2,FNis 2.26 kN when the pintle moves forward(③) and is 0.7 kN higher than FNwhen moving backward(⑦). The same result is found when comparing ④and ⑥.Until L=0 mm, FNin ①and ⑨are similar. The difference therein is only 0.1 kN, and therefore, it is observed that FNduring forward movement is different from that in backward movement at the same position; however, this difference is small at the end of a cycle. The performance of this pintle motor is therefore approximately periodic. It should be noted that the minimum FNdoes not occur at L=9 mm, and the time delay is 2 ms. When L=9 mm, FNis 0.99 kN, which is 34% higher than the minimum FN. The highest value of PCis also not found at L=9 mm, and the time delay is 2.5 ms.When the pintle is at ⑤, PCis 7.54 MPa, some 1.2% lower than the maximum PC. There is some oscillation in FPcurves when the pintle moves back,because the trend is for the shock waves to move forward, while the decrease in At,eqdelays the flow.Therefore,the differences between these two trends cause the aforementioned oscillations.It can be found that there is a tiny time delay between the changes in the chamber pressure,thrust, force on the pintle and the pintle movement. Furthermore,because there is a stroke with the same At,eq,it provides a buffer for parameter change.When the pintle moves back to the initial position, all parameters have little change with the initial value. Therefore, the parameter change caused by the reciprocating movement of the pintle is periodic.

Fig. 9 Pressure distribution along nozzle wall (PW) at different time.

Fig.9 shows that PWdecreases as the pintle moves forward from 0 to 21.5 ms, the pintle starts moving, At,eqdoes not yet change, and thus, PWon the nozzle wall decreases smoothly.From 21.5 to 26.5 ms,At,eqbegins to decrease.It is found that at the nozzle divergent section, PWdecreases, whereas away from the dashed line, PWchanges albeit only slightly. As for the nozzle throat, the pressure decreases to 1 MPa suddenly,which shows that flow separation occurs. Then from 26.5 to 35.5 ms, the pintle moves forward and At,eqcontinues to decrease. At this period, reflection shock waves appear in the nozzle fluid. Therefore, it is found that there is a sudden increase in PWon the nozzle divergent section, as also shown in Fig. 8(a). PWdecreases with At,eq, however, when At,eqis at its minimum value, PWdoes not. The minimum value of PWappears at about 41.0 ms,and then the pintle moves back.It is observed that the value of At,eqat 26.5 ms and 45.0 ms is the same;however,PWat 45.0 ms is about 1.2 MPa lower than that at 26.5 ms. When comparing PWat 50.0 ms and that at 21.5 ms,the same results can be found.PWat 50.0 ms is about 2.0 MPa lower than that at 21.5 ms.Finally,at 55 ms,the pintle reverts to its initial position and PWbecomes smooth again.The distribution of PWis similar to that at 0 ms. This shows that PWreverts to the initial condition after a cycle of pintle movement,and thus,the change of thrust is periodic as shown in Fig.8(b).It can be concluded that the flow separation point is moving forward with the pintle moving forward, and vice versa. The pressure in the nozzle throat is much higher when At,eqstays unchanged at 80.15 mm2than when At,eqchanges to be smaller.

3.2. Effect of pintle structure on performance (cold flow)

Three pintle structures are tested (Fig. 4). The gas supply system in cold test consists of high-pressure air bottles (Fig. 1),and the inlet gas pressure is stable.Therefore,the inlet boundary condition in the simulation is set to a pressure inlet. All pintle valves move from the left to the right in simulations.It should be noted that their initial positions are not the same due to the difference in working principles. Pintle velocities and lengths of pintle movements are set to the same values.Parameters used in these simulations are listed in Table 3.

Mach number contours during a round of movement with different pintle structures are illustrated in Fig. 10.

Fig. 10 shows that the fluids in the SD and DD cases are similar while that of the PD case is different. It is found that when the pintle starts moving forward at t=0 ms, the fluids in the SD and DD cases are similar to that in traditional SRMs. At,eqat this moment is 80.15 mm2, which is also the nozzle throat area, and therefore, the disturbance caused by the pintle to the flow field is small. As for the PD case, there is a large flow stagnation area near the plug head. Its centre flow rate is relatively low and at t=22 ms, L=6.6 mm,and oblique shock waves appear in SD and DD cases. The fluid near the pintle head is compressed. As for the PD, the flow velocity in the centre flow is slower. This is due to the increase in At,eq. Then, at t=30 ms, the pintle of SD and DD is the closest to the nozzle throat. The pintle moves 9 mm towards the nozzle, and At,eqis 5.81 mm2. There are strong shock waves generated, and because the gas flows through the passageway and expands the flow field in the nozzle,the main flow in the DD case is wider than that of the SD.As for the PD,the change in flow field is smaller.Then the pintle starts to move backward and when t=38 ms,L is 6.6 mm.Although At,eqis the same as at t=22 ms,their flow fields are different. The shock waves in SD and DD cases are much stronger than those at t=30 ms and t=22 ms. This shows that there is a delay in the flow field change relative to the pintle movement. Finally, at t=60 ms, the pintle reverts to its initial position. The flow field, in each design case, becomes smooth again.

Fig. 11(a) shows PWdistribution at two different time: the pintle starts moving forward at t=0 ms, Fig. 11(b) finishes a movement cycle at t=30 ms. It is found that PWin the PD case is always greater than the others. PWdistribution of SD and DD cases at t=0 ms are similar.At t=30 ms,their val-ues of At,eqdecrease to 5.81 mm2.The maximum PWin the SD decreases from 3.42 MPa (t=0 ms) to 0.31 MPa (t=30 ms).From Fig. 10, we can see that the reason for this may be the compression waves near the pintle: There is also a peak seen in the PWdistribution of 1.89 MPa at X=0.017 m in the DD case at t=30 ms,which is absent in the SD.The strengths of these shock waves are different and those in the DD case are much stronger than those in the SD case.

Table 3 Data used in simulations of different pintle structures.

Fig. 12(a) shows that, when the pintle moves continuously in reciprocating mode,the value of PCin the SD changes from 6.66 MPa to 7.27 MPa, the value of PCin the DD changes from 6.38 MPa to 7.26 MPa, and that in the PD remains at about 7.5 MPa. It is found that PCis steadier in PD than in others, and tends to increase continuously. The throat length in the PD case is longer than that of the others, which causes changes in PC.Then PCchanges in SD and DD cases are compared: their maxima are similar, while the difference is only 0.1 MPa, but the differences in their minima are significant at 0.28 MPa. The flow is block by the slit between the pintle and the partition, so the actual value of At,eqis smaller than predicted. This causes a ‘‘platform” in PCnear the minimum value in SD. As for DD, there is a drainage passageway on the pintle head. Therefore, a partial gas circulation is created between the cavity and the pintle head. So PCchanges more linearly in the DD case, and the change therein is larger.Besides this, it is found that the frequencies of oscillation PCin SD and DD are the same (16.67 Hz). This indicates that the structural optimisation of DD does not change the thrust regulation frequency.

Fig.12(b)shows that, when the pintle moves in reciprocating mode, the value of PVin the SD increases from 6.82 MPa to 7.07 MPa, the value of PVin the DD increases from 6.60 MPa to 7.03 MPa, and that in the PD increases from 7.51 MPa to 7.64 MPa.This is due to the structural characteristics. The value of PVof PD is closer to PCthan others,because its cavity is connected to the combustor in this design.Besides,because the gas in the cavity mainly flows through the slit, PVis less sensitive than PC. The theoretical maximum pressure cannot be reached within one cycle; therefore, differing from PC, PVincreases continuously. Then it is found that PVin the DD case rises faster than in the SD case. The first reason is the lower initial value of PVin DD, and the second reason is the presence of the drainage passageway.

The thrust from different pintle structures is shown in Fig. 13. It is found that FNfor each design changes periodically. FNof SD changes from 0.83 kN to 3.49 kN, FNof DD changes from 1.40 kN to 3.18 kN, and in PD it changes from 0.48 kN to 1.49 kN. It is observed that the thrust ranges of SD and DD are similar, while that of PD is lower. Besides,kmaxvalues for SD, DD, and PD are 4.20, 2.27, and 3.10 respectively, so the thrust regulation performance of SD is the best, while that of DD is the worst.

Fig.14 shows that the directions of FPare different for different pintle structures.The direction of FPdepends on the relative pressure integral before and behind the pintle. When the pressure integral in front of the pintle is higher, FP<0 and it is in the direction X>0.When the pressure integral in front of the pintle is lower, FP>0 and it is in the direction X<0.Then FPof SD changes from to -0.45 kN to 1.25 kN, FPof DD changes from-0.55 kN to 1.00 kN,and FPof PD changes from -1.61 kN to -0.50 kN. It is observed that the range of oscillation of FPof PD is the narrowest, and FPremains in the same direction, because the pressure around the plug stem is always larger than the plug head and its FPis always in the direction X>0.As for SD and DD,DD is smaller regardless of the range or the maximum value of FP.This proves that DD can effectively reduce the payload of a pintle motor with a minor thrust loss, matching conclusions reached elsewhere.15

In this subsection, it can be concluded that these three pintle structures have their different characteristics.The SD has a widest thrust regulation range. At the same time, the pressure in its cavity is higher,and this leads to an undesired load on the control system. Therefore, it can be found that its FPis the highest. Then DD can balance this pressure differences effectively.This makes it a lower FPthan the standard design.However, the thrust regulation performance has a little degradation. Finally, the thrust of PD is the smallest, while the thrust regulation ratio is at the same level as the others.Besides, it is the only design whose direction of FPstays the same during pintle movement.

3.3. Effect of pressure exponent of solid propellants on performance (hot flow)

In real rocket motors, solid propellant is burned to generate high-pressure hot gas,which is ejected from the nozzle to generate thrust. AP/HTPB composite propellant without aluminum is chosen for hot test. The reason is that there is a risk of nozzle clogging, and a fast pressure build-up process is desired. The propellant parameters used in numerical simulation of hot flow are based on Ref.1 and Ref.19.The density of the propellant is 1800 kg/m3, and the burning rate of it is 4.118×P0.25mm/s. To study the effect of the pressure exponent, the pressure exponent are changed in the simulation.Accordingly, the rate of burning of the propellant is affected by the chamber pressure. To elucidate the working characteristics of a pintle motor in real conditions, solid propellant is burned in the combustor (Fig. 1). In simulations, the inlet boundary condition is set to a mass flux inlet. It should be noted that the inlet area of the numerical simulation is not the actual propellant burning surface which is much larger in the combustion chamber. Therefore, a magnification factor of the burning surface should be considered in the simulation.In this section,the effect of changes in pressure exponent of the propellant is studied.

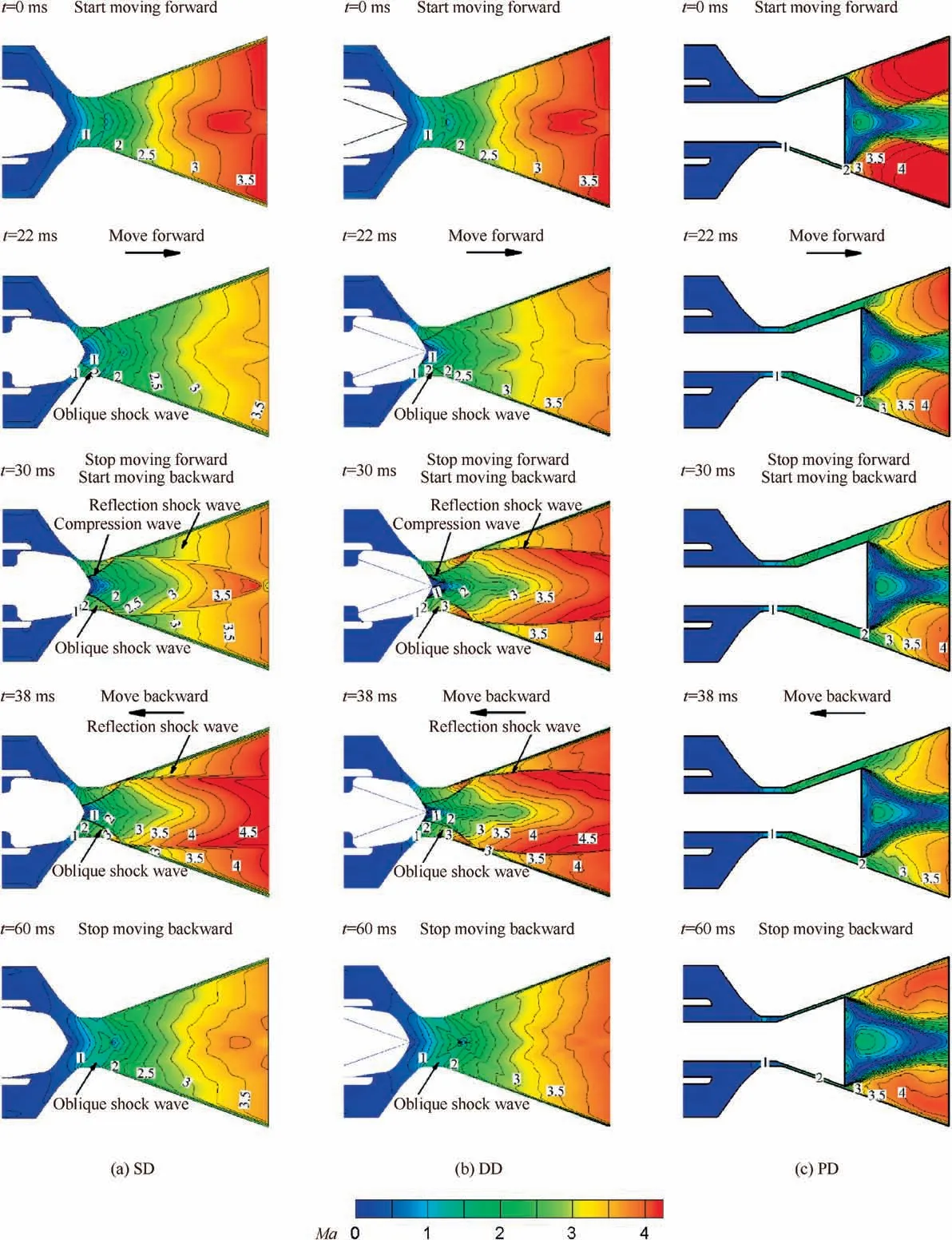
Fig. 10 Mach number contours at different time.

One of the most important parameters in a hot test is its pressure exponent (n). As shown in Eq. (14), the propellant burning rate is proportional to n and thus thrust in hot test is sensitive to n. Transient simulations with different n are performed using a User-Defined Function (UDF). Lengths of pintle movement (L) in this section are all 7.2 mm, so the minimum At,eqin this section is 47.02 mm2. Parameters used in the simulations are listed in Table 4, where Φ is the mass flux of the inlet, and p is the local pressure at the inlet.

Fig. 11 PW of different pintle structures at different time.

Fig. 12 Variation of pressure with time for various pintle structures.

Fig. 13 Variation of FN with time for various pintle structures.

Mach number contours with different n when the pintle just stops moving (t=22 ms) are shown in Fig. 15.

Fig. 15 shows that distributions of Mach number are similar regardless of n.It can be found that the Mach number distributions of a pintle motor are mainly determined by the structure of the motor and the design of the pintle, regardless of n. Besides, there are also strong oblique shock waves and reflection shock waves generated in the hot test.

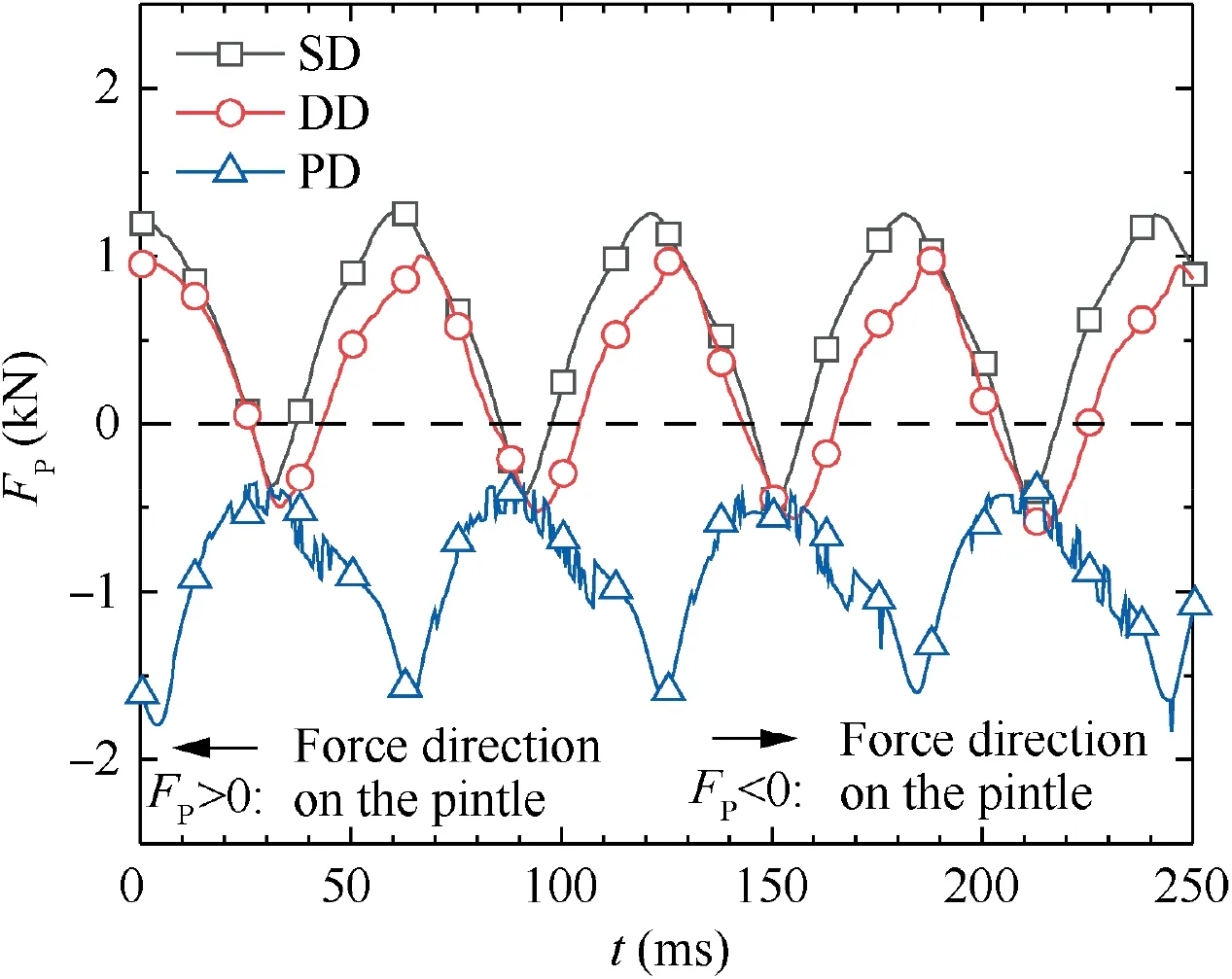
Fig. 14 Variation of FP with time for various pintle structures.

Fig. 16 shows that n has a significant influence on the final value of PC,and the response time(τP)increases with different n. Although At.eqin all cases decreases from 80.15 mm2to 47.02 mm2,the changes in PCare very different.The initial values of PCfor D1 to D4 are 2.05 MPa,3.29 MPa,4.18 MPa and 6.01 MPa, and the final steady values of PCfor D1 to D4 are 4.25 MPa, 11.10 MPa,17.95 MPa,and 36.82 MPa. It is found that the greater n is,the greater the change in PCis.The values of τPare 0.3 s, 0.9 s, 1.3 s, and 1.7 s for D1-D4. It is observed that it takes longer for PCto become stable than in a cold test and it takes longer for PCto become stable at higher n.Hence a higher n means a higher change in performance with regard to PC,which imposes more onerous requirements on the structural strength of the combustor.

Fig.17 shows that the mass flow rate and thrust regulation ratio are greatly affected by n. It is found that ˙m is monotonically increasing, while k is non-monotonic. The initial values of ˙m for D1 to D4 are 0.47 kg/s, 0.75 kg/s, 0.95 kg/s, and 1.37 kg/s; the final steady ˙m values for D1 to D4 are 0.47 kg/s, 1.22 kg/s, 1.97 kg/s, and 4.06 kg/s. Compared to the initialvalues, the magnification multiples are 1.00, 1.63, 2.07, and 2.96.It can be concluded when n is higher,both the final steady m˙ and its magnification multiples are higher.Then values of τmof D1 to D4 are about 0 s,0.6 s,1.1 s,and 1.7 s.It is observed that the lower n is,the faster m˙ stabilises.Then it is found from the detailed picture(Fig.17(b))that the values ofof D1 to D4 are 1.06 kN,1.70 kN,2.16 kN,and 3.11 kN,and therefore,k of D1 to D4 all start to change from 1.00, and decrease to 0.53 at 23 ms. Then k begins to increase, reaching 1.01, 1.66,2.12,and 3.02.It can be concluded that the minimum k values during the process are the same regardless of n, although the actual minimum FNis different (0.56 kN, 0.91 kN, 1.16 kN,and 1.65 kN). Considering that the time of pintle movement is 22 ms,the decrease in k is caused by flow reduction at lower At.eq.The minimum value of k during this decrease is the same regardless of n,and the time at which it occurs is around when the pintle stops.Then k increases because of an increasing PC,and therefore, the higher n is, the higher the final k value is.Finally, the values of τkfor D1 to D4 are about 0.59 s,0.99 s, 1.38 s, and 1.89 s. It can be concluded that the lower n is, the more rapidly k stabilises.

Table 4 Data used in simulations with different burning pressure exponents.

Fig. 15 Mach number contours at 22 ms with different n.

Fig. 16 Variation of pressure with time for different n.

Fig. 17 Variation of ˙m and k with time for different n.

Fig. 18 shows variation of FPwith different n. The initial values of FPare 0.65 kN, 1.04 kN, 1.32 kN, and 1.90 kN,respectively. They decrease to 0.28 kN, 0.45 kN, 0.57 kN,and 0.82 kN, at about 23 ms. This decrease is caused by the pintle movement. Then FPincreases to 0.53 kN, 1.39 kN,2.24 kN, and 4.58 kN, and stabilises at 0.38 s, 0.87 s, 1.23 s,and 1.73 s. It is found that the lower n is, the more rapidly FPstabilises. Besides, it is observed that the time taken for FPto become stable is longer in hot tests than in cold tests.This indicates that the combustion feedback process takes longer than the changes in flow.

Finally, to compare the changes in PC, ˙m, FN, and FPwith different n,a and b are defined to show the effect of n thereon.The magnification of n for one parameter is represented by a,and can be calculated as

where subscript‘‘stable”represents the final stable value of the parameter, and subscript ‘‘initial” represents the initial value of the parameter. The connection between this magnification and n is represented by b.In other words,b is the magnification of a for one parameter. It can be calculated as

where an=n0represents the value of a when n=n0,and an=0represents the value of a when n=0.

Fig. 18 Variation of FP with time for different n.

Then amplification of different parameters with different n is shown in Fig. 19.

It is found that magnification of n by different parameters varies (Fig. 19(a)), while the amplifications for different parameters are the same (Fig. 19(b)). Fig. 19(a) shows that n has the most obvious effect on PC,and the least obvious effect on FP. When n changes from 0 to 0.6, the value of a for PCchanges from 2.1 to 6.1, which indicates that the larger n is,the more PCchanges during pintle movement (the changes of ˙m and FNare identical). When n changes from 0 to 0.6, a thereof changes from 1.0 to 3.0, which shows that the propellant burning rate is the main control factor of the thrust change in the hot test. Fig. 19(b) shows that changes of b are only related to n regardless of other parameters. When n changes from 0 to 0.6, b changes from 1.0 to 3.0 for all other parameters, and therefore, it is concluded that the amplifications of PC, ˙m, FN, and FPare all determined by n to the certain same value during pintle movement.

In this subsection,it can be concluded that n is an extremely important factor in the hot test of SRM with a pintle valve.Both P and k increase obviously with the increase of n.Besides, it was observed that the changes of P, k and FPdo not increase monotonically over time. They decrease first and then increase to the stable value. The reason is that the effect between chamber pressure and burning rate feedback takes some time to manifest. Before this, the influence of the pintle movement on the flow field is more obvious. Finally,magnifications of n for different parameters are different.However, these amplifications which vary with n for different parameters are the same.

4. Conclusions

Thrust control plays a critical role in improving the control performance of solid rocket motors.To promote effective pressure and thrust regulation,optimisation of pintle structure and propellant pressure exponent may have potential to be applied in pintle motors. In this work, 2D RANS simulations of the SRM non-reacting flows with pintle valves are performed.The validation results show that the current numerical model with the two-equation RNG k-ε turbulence model can provide good agreement with the experimental pressure data with a discrepancy of less than 2% therein.

Fig. 19 Amplification of PC, ˙m, FN, and FP with different n.

The effects of three pintle structures(standard design,drainage design, and plug design) with the same length of pintle movement are evaluated. It is found that the standard design has the highest maximum thrust regulation ratio of about 4.20. The drainage design can effectively reduce the payload of a pintle motor for 0.2 kN with only slight loss of thrust despite sacrificing some thrust regulation performance. The plug design can achieve a large range of thrust regulation in application in a low-thrust system, and the direction of the force on the plug remains unchanged.

Moreover,the effects of the propellant pressure exponent at four different values (0, 0.4, 0.5, and 0.6) are evaluated. It can be concluded that the pressure exponent is one of the most important parameters in a hot test. The thrust regulation ranges are larger when the pressure exponent is higher, which are consistent with the changes in propellant burning rate.When n increases from 0 to 0.6, the thrust regulation ratio increases from 1.00 to 2.96. At the same time, the chamber pressure also increases with increasing n.When n changes from 0 to 0.6,the value of a for PCchanges from 2.1 to 6.1.Besides,the amplification of PC, ˙m,FN,and FPwith different values of n differs; however, an interesting finding that the ‘‘amplifications of these amplifications” are all the same for different parameters was noted. With reference to the amplification at n=0, when n changes from 0 to 0.6, the ‘‘amplifications of these amplifications” for different parameters all change from 1.0 to 3.0.

Acknowledgement

This study is supported by the National Natural Science Foundation of China (No. 11572042).