Numerical investigation on flow nonuniformityinduced hysteresis in scramjet isolator

Tinglong HUANG, Linjie YUE,*, Shenghu MA, Qifn ZHANG,Peng ZHANG, Xinyu CHANG

a State Key Laboratory of High-temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences,Beijing 100190, China

b School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China

c Department of Mechanical Engineering, the Hong Kong Polytechnic University, Hong Kong, China

KEYWORDS Adverse pressure gradient;Back pressure;Hysteresis effects;Non-uniform flow;Shock train

Abstract Numerical simulation and theoretical analysis were conducted to study the hysteresis inside scramjet isolator during the reciprocating process of back pressure variation. It is revealed that only a regular reflection is theoretically possible for two leading shocks when the inflow Mach number is greater than 2.0, and no hysteresis can occur in the transition between shock reflection types. Nevertheless, wall suction, gas injection, and background waves cause non-uniformity of the incoming flow and would make hysteresis possible. Besides the classical hysteresis in the transition between shock reflection, new kinds of hysteresis were found in both the deflection angle of separated boundary layer and the location of the shock train.Moreover,the occurrence of hysteresis in the deflection angle of the separated boundary layer is accompanied with the shock reflection hysteresis.In the case with background waves or gas injection,hysteresis in the starting position of leading shock was observed too.As back pressure decreases,the leading shock does not follow the same path as that as the back pressure increases,and it is anchored at the location where the background shock or the injection interacts with the leading shock. It is inferred that, if two strong adverse pressure gradient regions move towards and interact with each other, hysteresis will take place when they start to separate.

1. Introduction

Dual-mode scramjet engine is expected to be a promising candidate for the propulsion unit of future space transportation systems.As a critical component,the isolator module is a constant or nearly constant area duct located between the inlet and the combustor of a scramjet.1In response to the pressure rise associated with heat release in the combustor, a precombustion shock train appears in the isolator to prevent the inlet unstart.

Nomenclature

Cf0skin-friction coefficient

DS dominant separation region within the shock train

H height

L length

Ma Mach number

MR Mach reflection

p static pressure

P0total pressure

PR back pressure ratio

Q pressure coefficient related to Reynolds number

Re Reynolds number

RR regular reflection

S2, S3, S4 location: background shock impinges into the wall

SWBLI shock wave/boundary layer interaction

T static temperature

T0total temperature

x streamwise coordinate

y+the height of the first mesh cell off the wall in wall coordinate

Greek letters

α attack angle

β shock wave angle

γ specific heat ratio

Γ shock polar curve

θ deflection angle of separated boundary layer

δ boundary layer thickness

Sub/superscript

0 total or stagnation state

1 location: upstream the shock train or the isolator entrance

2 location: downstream the leading shock

3 location: downstream the reflected leading shock

’ location: near the upper wall

∞ free stream conditions

b location: isolator exit

D detachment criterion

j gas injection location

L lower leading shock

s starting position of shock train

S3 the third reflection point where background shock

strikes the wall

U upper leading shock

VN Von Neumann criterion

Because of the important function of the isolator for scramjets,lots of control measures were studied to enhance its ability to resist back pressure within a limited isolator length. Weise and Olivier2,3studied the effect of the boundary-layer suction on the shape of the shock train and found that the suction slots serve to remove the boundary layer and the slots can stabilize the leading shock, which is the first shock of a shock train.Other techniques,such as vortex generators,ramp,and passive cavity, have also been studied4,5for their ability to resist the back pressure by suppressing boundary-layer separation.

The flow structure of Shock-Wave/Boundary-Layer Interaction (SWBLI) inside the isolator usually takes the form of shock train. In the past decades, the SWBLI phenomenon has been studied extensively. It has been recognized that the SWBLI is largely influenced by the Reynolds number and the flow Mach number just upstream the shock train.5-8If the freestream Mach number is less than 1.3 or so, the flow structure is a single normal shock with a certain curvature near the wall; the boundary layer may not separate or separates only at the foot of the shock, but it has a strong tendency towards reattachment. If the Mach number is between about 1.3 and 1.5,a single,nearly normal shock with bifurcated ends occurs as the result of large-scale boundary layer separation,showing a weak tendency towards reattachment.For the Mach number over 1.5 or so, a shock train consisting of a series of shock waves appears. According to the reflection patterns for two leading shocks, the shock train can be classified as a normal one at lower Mach numbers and an oblique one in the Mach number range of 1.8-2.5.5Many researchers5,9,10have reported that increasing the free stream Mach number enhances the asymmetry of the shock train pattern, even in symmetric flow passages and under uniform inflow conditions.Such an asymmetry manifests as that one side of the separation region within the shock train is dominant over the other.As a part of the scramjet, the isolator has, in fact, a non-uniform inflow condition.The complex background shock waves introduced by the inlet device always exist in the isolator,leading to a flow field with large stream-wise and transverse nonuniformity in the upstream of the shock train. Tan et al.11,12found that the background shock waves and expansion waves changed significantly the flow characteristics of the shock train. They observed that the dominant separation region shock was attached to the upper and the lower walls successively when the shock train moved upstream.When the leading shock arrives at the impingement points of the background shock,the shock train will suddenly move forward,as pointed out by Chang et al.13Li et al.14,15proposed a method to predict the shock train path with background waves. The results indicate that the local parameters govern the shock train’s motion, and the pressure gradient along the surface plays an extremely important role.Xu et al.16combined free interaction theory with limit theory to explain the rapid movement of shock train under the incident shock condition.

Within the shock train, the shock/shock interference manifests itself between two leading shocks and between their subsequent reflection shocks. Between two shocks there are two interference patterns,such as Mach Reflection(MR)and Regular Reflection(RR).Von Neumann introduced the Von Neumann criterion and the detachment criterion to predict the transition between MR and RR,17,18and these two criteria predict a hysteresis in the transition, which was first hypothesized by Hornung et al.19,20The RR →MR transition takes place near the detachment criterion with increasing wedge angle, whilst the MR →RR transition takes place at the Von Neumann criterion with decreasing wedge angle.Chpoun et al.21firstly captured the hysteresis phenomenon in experiments.Shimshi22and Setoguchi23et al. considered the viscous effect and observed the shock reflection hysteresis.By combining the free-interaction theory with the shock reflection hysteresis theory, Tao et al.24proposed a detailed analysis to describe the shock reflection patterns in SWBLI. They found a shock reflection hysteresis similar to the one existing in the reflection of symmetric shock waves.In addition,the hysteresis can be achieved with asymmetric wedges by changing the free stream Mach number and the downstream pressure,or the distance between two wedges.22

Regardless of the above noteworthy advances, the finding of new hysteresis phenomena in the isolators in recent directconnected combustor experiments25-29and numerical simulations30,31captured considerable attention. The results show that the wall pressure distributions and the Mach number at isolator exit depend not only on the fuel equivalent ratio but also on its variation.Apparently,this is not conducive to accurate flight control. These studies attempted to elucidate the mechanism of this hysteresis from the perspective of combustion and pointed out that the hysteresis was observed in the transition between ramjet and scramjet mode.28,29Nevertheless, the combustion mode was determined by the minimum Mach number calculated from the one-dimensional analysis.Such one-dimensional analysis has a large uncertainty concerning the flow patterns and neglects the evolution of the local flow, and thus it cannot provide convincing evidence for clarifying hysteresis mechanism.

The mechanism of hysteresis in the isolator flow has not been studied without the influence of combustion. The inconformity in wall pressure distributions and the Mach number at isolator exit implies that the location of the shock train can be different for the same fuel equivalent ratio within the hysteresis region. Hence, the present study aims to gain a better understanding of the physics governing the hysteresis process by using numerical simulation to obtain detailed flow structures and motion characteristics of the shock train. Many common disturbances, such as wall suction, background waves, and jet injection, were taken into account in the present simulation.The shock train was generated by imposing a high back pressure condition at the isolator exit so as to avoid the complication caused by combustion.

2. Numerical methodology

2.1. Numerical methods

The unsteady Reynolds-averaged Navier-Stokes equations are numerically solved by the finite volume method, using a density-based implicit solver, with a second-order upwind discretization scheme for two-dimensional turbulence flow. The numerical flux through each cell face is evaluated by the AUSM scheme, and the turbulence model of k-ω SST is employed with a compressibility correction for high Mach number flows. In order to ensure the calculation accuracy in the boundary layer, the meshes adjacent to the walls are refined to satisfy y+≤1.At all solid surfaces,no-slip adiabatic conditions are imposed. The fluid is treated as a compressible perfect gas with compositions of standard air. The incoming flow boundary is set as a pressure inlet condition, and the isolator exit is set as a pressure outlet condition. To generate a shock train, a high-pressure condition is adopted at the pressure outlet condition. All the two dimension simulations were conducted by using the ANSYS Fluent.

2.2. Experimental validations

In order to validate the present numerical methods, we simulated the internal compression of a hypersonic inlet tested by Herrmann32and Reinartz33et al. The inlet configuration is shown in Fig. 1, where the attack angle α=-10°, the flow Mach number Ma∞=2.41,the total pressure P0and the total temperature T0were specified as 0.54 MPa and 305 K, respectively.To ensure grid independence,we adopted three different grids such as the coarse (500×60), the fine (1000×120) and the dense (1990×240).

Fig. 2 presents the experimental Schlieren image and numerical results obtained from different grids under the condition when the inlet is fully started.It can be seen that the flow structure and shock waves are well captured by the simulations using different meshes,and the finer mesh provides more sharp flow details than the coarse one. Fig. 3 shows the streamwise distributions of the upper surface pressure. Compared with the experimental pressure distribution, the numerical results from the fine and dense grids show a good agreement, but the results from coarse grids exhibit some difference. The fine mesh was adopted by the study for the following results as a balanced choice of computational cost and accuracy.

Fig. 1 Main dimensions of the model32 (α=-10°,δ2=-21.5°, δ3=-9.5°, δ4=5°, h=15 mm, see the origin reference for details).

Fig.2 Comparison of experimental Schlieren image and numerical Mach number contour lines with a low back pressure ratio(PR) for different meshes.

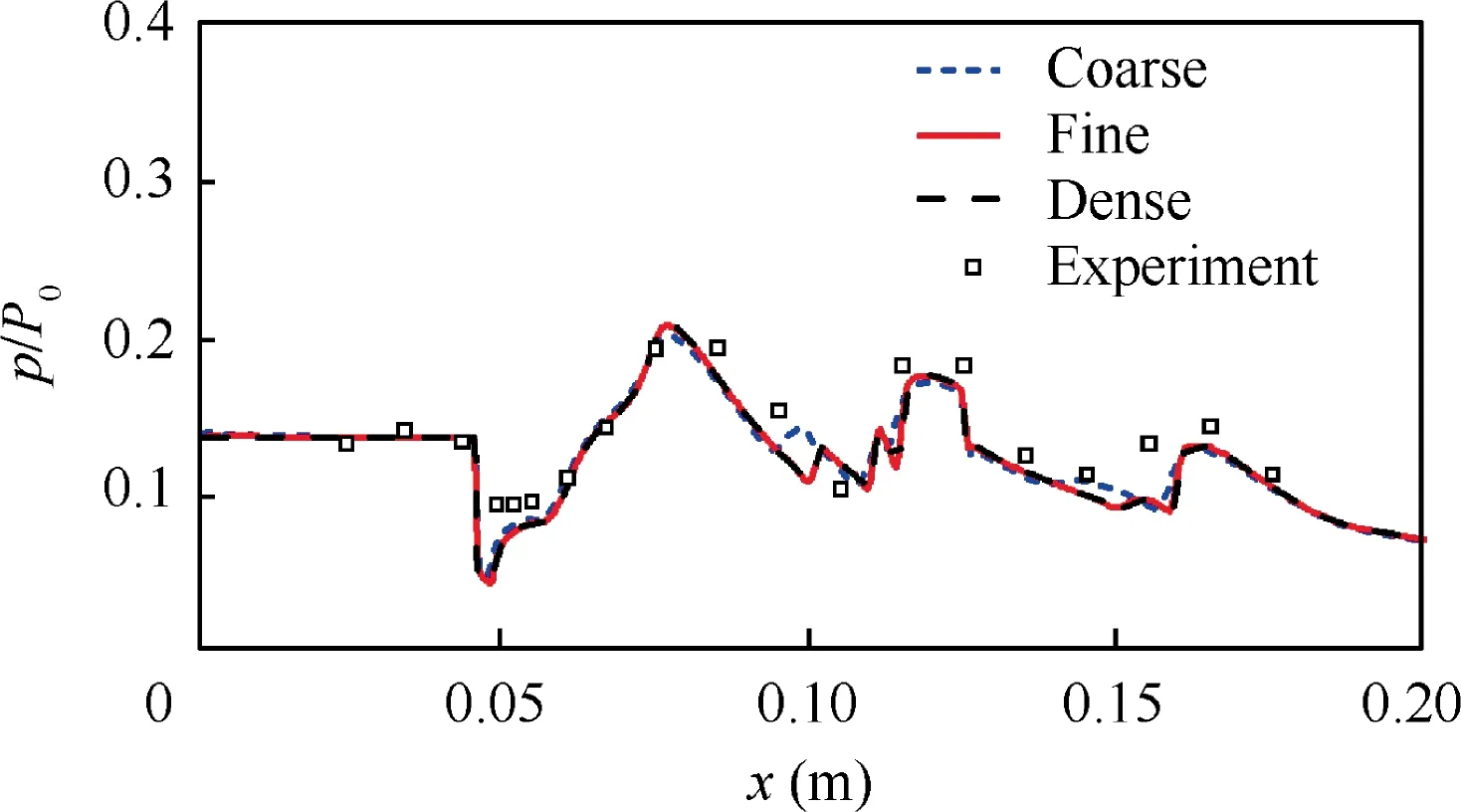
Fig. 3 Experimental and numerical pressure distributions on ramp wall.

Fig. 4 Comparison of an experimental schlieren image and numerical Mach number contour for a specified back pressure ratio of 7.

Fig. 5 Comparison of pressure distributions on both lip and ramp walls between experimental and numerical results from the fine grid scheme.

Fig. 4 shows the comparison of an experimental Schlieren image and numerical results for a specified back pressure ratio of 7.0,whilst the corresponding wall pressure distributions are shown in Fig. 5. Good agreement can be seen between the numerical and the experimental results. Overall, the methods used in the study have quantitatively satisfactory accuracy in calculating the internal flow with or without throttling at the duct exit.

3. Shock train under the uniform incoming flow conditions

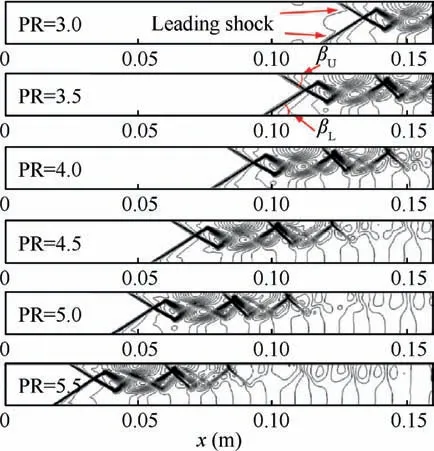
Fig. 6 Pressure contours under uniform incoming flow conditions (Ma1=2.5, Re=2.09×107 m-1, PR=3.0-5.5).

In this section, the motion characteristics of the shock train will be investigated to examine whether a hysteresis phenomenon takes place in an isolator under the uniform incoming flow conditions. Fig. 6 shows the pressure contours at different back pressure ratios for the incoming flow of Ma=2.5. The isolator has a length of 160 mm and a height of 16 mm.The back pressure ratio(PR)is defined as PR=pb/p1, where p1is the static pressure of the incoming flow and pbthe static pressure at the isolator exit. It is seen that a sufficiently high back pressure can generate an oblique shock train and that as increasing PR,multiple shock waves arise to match the back pressure.There is an asymmetry in the oblique shock train as such the shock train is closer to the upper wall,meaning the dominant separation region adheres to the lower wall.As discussed in Introduction, the origin of the shock wave asymmetry is an unsolved problem and deserves detailed study. However, it is beyond the focus of the present study and will be considered in the future. In addition, the leading shock angles remain hardly changed at different back pressure ratios as listed in Table 1.Besides,the leading shock angle with respect to the lower side, βL, is slightly larger than that to the upper side, βU, manifesting the asymmetry.

The flow field near the leading shock of shock train can be divided into four different zones, as illustrated in Fig. 7. Zone 1 is the upstream region of the shock train, which is not affected by the back pressure; Zone 2 and 2′are the regions after the leading shocks; Zone 3 and 3′are the regions after the reflected shock; Zone 4 is the separation zone where the flow deflection angle θ in Zone 2 is identical to the deflection angle of the separated boundary layer. If θ is smaller than Von Neumann criterion, the leading shocks are of regular reflection, as shown in Fig. 7(a); if θ exceeds the detachment criterion, two leading shocks will take the form of Mach reflection, as shown in Fig. 7(b).

The leading shocks can be predicted by the free-interaction theory proposed by Chapman et al.34The flow properties in the vicinity of separation point and the pressure in the separation zone are dependent only on the upstream flow Mach number, the Reynolds number, and the upstream boundary layer condition. The downstream back pressure cannot affect the shock strength of the leading shock. In the light of freeinteraction theory, the plateau pressure in the separation region can be calculated by,

Table 1 Shock angles of two leading shock waves under uniform incoming flow conditions.

Fig.7 Schematic of interference between two leading shocks of a shock train.

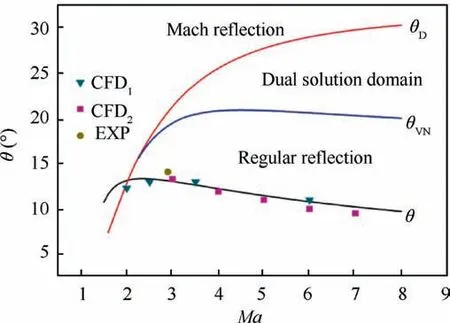
Fig. 8 Variation of the deflected angle of separated boundary layer with Mach number.

where Cf0is the skin-friction coefficient of the boundary layer,Ma1is the Mach number of incoming flow, p1is freestream static pressure, Q is a pressure coefficient related to the Reynolds number. For an upstream fully developed boundary layer with a moderate Reynolds number based on the boundary layer thickness (3×104≤Reδ≤1.2×106), the plateau pressure in the separation region is dependent on the free stream Mach number only,35as follows.

The isolator flow is generally of moderate Reynolds number. Thus combining the Rankine-Hugoniot relationship and Eq. (2), the leading shock wave angle βLand boundary layer deflection angle θLcan be determined by

According to Eqs.(2)and(3),the angle of leading shock is equal to 35.14° which is slightly larger than the measurement.This model is also compared with the numerical and experimental results, as shown in Fig. 8, where θ is predicted by Eq. (4), CFD1is the present numerical results, whilst numerical results CFD2and experimental results (EXP) are adopted from Wang et al.36. θDis the detachment criterion and θVNis Von Neumann criterion.Through the contrast of the predictions of the theoretical model and the results from simulations and experiments,the theoretical model is proved to be reasonably reliable. Furthermore, the theoretical model shows that the deflection angle of the separated boundary layer is firstly increased and then slightly decreased as the Mach number increases.

The intersection of the θ and θDcurves indicates that the reflection pattern of two oblique leading shocks is Mach reflection for Ma1<2.0. For Ma1>2.0, the value of θ is always smaller than that of the Von Neumann criterion θVN, which means the reflection pattern of leading shock can only be RR for a fully developed boundary layer,and thus no hysteresis can occur in the transition of reflection type.

In order to examine whether there are any kinds of hysteresis in the shock train,the motion characteristics were obtained for a reciprocating process of PR variation,as shown in Fig.9 for the Mach number contour and in Fig.10 for the wall pressure distributions.As can be seen,both the Mach number contour and the pressure distributions depend on the back pressure ratio only, which means that there is no hysteresis in the isolator under the condition of uniform flow.

4. Hysteresis in the isolator shock train under non-uniform inflow conditions

In practical engineering applications, the incoming flow in the upstream of the shock train is usually non-uniform due to many factors, including wall suction, background waves, and jet injection, which can significantly impact the shock train structure and may cause hysteresis in the isolator.This section is devoted to studying the influence of non-uniform incoming flows on the motion characteristics of shock train.

4.1. Hysteresis caused by wall suction

As a widely-used method to improve the capability of resisting the back pressure, wall suction invalidates the free-interaction theory by anchoring the leading shock at the suction slot.Therefore, we performed numerical simulations to obtain the motion characteristics of the shock train with wall suction in the reciprocating process of PR. As shown in Fig. 11, there are three normal slots with 4 mm in width and 4 mm in spacing evenly mounted on both walls of the isolator. The spacing between the isolator entrance and the first slot is 88 mm. At the incoming flow boundary,the pressure inlet is imposed with Mach number Ma1=3.5, static pressure p1=87670 Pa, and static temperature T1=587.6 K. At the slot exits, a pressure outlet with the low-pressure condition is used.

Fig. 9 Mach number contours under condition of uniform incoming flow at Ma∞=2.5.

Fig. 10 Wall pressure distributions under condition of uniform incoming flow.

Fig. 12 presents the Mach number contours in the isolator with wall suction for various PR.The whole process of increasing PR can be classified into four typical phases. In Phase Ⅰ(e.g. at PR=5.0), the foot of leading shocks has not reached the location of the suction slot; the boundary layer deflection angle and the leading shock wave angle remain the same as the back pressure rises.In Phase Ⅱ,the leading shocks are stabilized at the suction slot and only RR is observed. With increasing PR, the deflection angle and leading shock wave angle will increase in order to match the back pressure. In Phase III, MR occurs between two leading shocks. When PR is increased to 12.9, the flow deflection across leading shock is greater than the detachment criterion,and the reflection pattern of leading shocks transitions from RR into MR. In addition, the length of Mach stem varies with back pressure. In Phase Ⅳ, a leading shock arrives at the middle suction slot when the PR is increased to 14.5. After this phase, the transition from MR to RR takes place at PR=11.7 during the decrease process of PR.Obviously,a hysteresis occurs in terms of shock reflection transition,and Fig.13 clearly shows the lag loop represented by the length of the Mach stem.

According to the results in Section 3,the MR cannot occur at Ma=3.5 for uniform inflows. Thus, the observed MR structure must be attributed to the wall suction because it enhances the capability of isolator in shock holding. When the back pressure becomes sufficiently large, the boundary layer deflection angle θ becomes so large to result in a large leading shock angle β to cause Mach reflection.

Fig. 11 Sketch of model isolator with wall suction.

Fig. 12 A hysteresis loop of Mach number contour in isolator with wall suction.

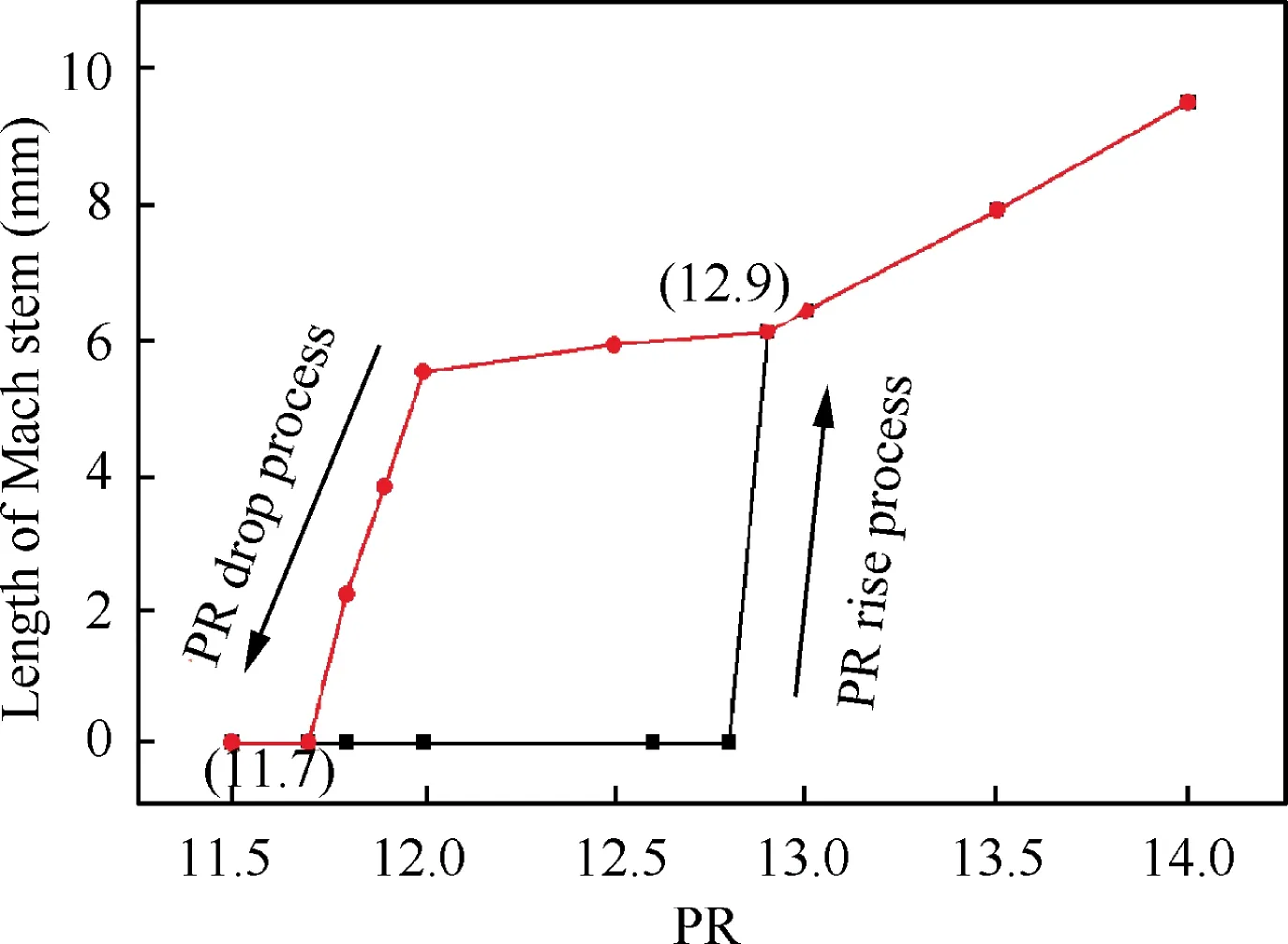
Fig. 13 A hysteresis loop of Mach stem length with back pressure ratio.

The transition between RR and MR showed in Fig.12 can be better understood by considering the shock polar representation shown in Fig.14.Polar Γ1represents the leading shocks.The polar curves Γ2and Γ3are associated with the conditions after a deflection angle θLand θU. At PR=12.8, the polar curves Γ2and Γ3are nearly tangential, indicating that the detachment criterion is nearly reached.The RR →MR transition will happen once the back pressure ratio increases further to 12.9,as shown in Fig.12.Similarly,at PR=11.8,the polar curves Γ2and Γ3nearly intersect at the Von Neumann criterion, which means that the Mach stem will disappear if the back pressure further decreases. In general, the transition between RR and MR conforms to the shock polar analysis together with the Von Neumann and the detachment criteria.

Fig.15 shows a lag loop of the lower boundary layer deflection angle θLwith PR. As PR increases, the θLhas a sudden rise at PR=12.9 where a Mach stem appears. When PR decreases, the θLhas a sudden drop at PR=11.7 where the Mach stem disappears.The lag loop suggests that another kind of hysteresis phenomenon exists in terms of the deflection angle of the separated boundary layer, which has not been reported in the literature according to the knowledge of the authors.

Under the condition of wall suction, the flow structures exhibit two different kinds of hysteresis phenomena in terms of the transition between RR and MR and the flow deflection angle of the separated boundary layer.To understand the relation between these two kinds of hysteresis phenomena,we first noted that, there is no hysteresis in θ for PR ≤11.7 or PR ≥12.9,and the hysteresis in θ is accompanied with the hysteresis in shock reflection type. Moreover, the hysteresis in shock reflection type induces that in deflection angle θ.Fig. 16 shows the pressure distributions along the lower wall and indicates that the pressure rise across the leading shock of MR structure is larger than that across the RR structure.The leading shock angle and the corresponding θ are thus different for the same PR. When a hysteresis in the transition of shock reflection takes place, a hysteresis occurs in θ as well.

Fig. 14 Shock-pattern interpretation in shock polar diagram.

Fig. 15 A hysteresis loop of lower boundary layer deflection angle with PR.

Fig. 16 Comparison of pressure rise across leading shock between two reflection types at PR=12.0.

4.2. Hysteresis caused by background shock waves

The actual flow in the scramjet isolator is very complex due to the unavoidable background waves, including the incident shock induced by inlet cowl, the expansion waves, and their subsequent reflected waves. The background waves generate gradients of flow parameters in the isolator, and therefore the incoming flow in the upstream of the shock train is nonuniform and asymmetric. The motion characteristics of shock train under such inflow conditions would be different from those under uniform inflow conditions.

To study the influence of background shock waves, a simplified model was designed to investigate the motion characteristics of the shock train. In this and the following sections, all the isolators have a height (H) of 16 mm and a length (L) of 160 mm, which are the same as the model dimensions in Section 3. The complex flow field due to the inlet was treated as a cowl shock and a shoulder expansion fan. As shown in Fig.17,AB is the isolator entrance and its flow is divided into two parts:the flow at OA is the free stream flow and that at OB is of the type after a cowl shock wave. The attack angle α is 10°, the Mach number at OA and OB are Ma∞=2.5 and Ma1=2.08 respectively. Fig. 18 presents the Mach number contour and static pressure contour without shock train. As can be seen, the background shock wave firstly hits the lower wall, and the intensity of subsequent reflected shock waves and expansion waves gradually weaken along the streamwise direction. This section focuses on the motion characteristics of the shock train in the region of the second reflection point(S2) and the third reflection point (S3) during the process of reciprocating variation of PR.

Fig.19 shows the Mach contour and presents the propagation of the shock train during the reciprocating process of PR variation.At PR=3.2,the Dominant Separation(DS)region adheres to the upper wall. The foot of leading shock on the lower wall has not yet reached the reflection point S3 until PR increases to 3.4. Then DS switches to the lower wall with a sudden upstream movement. As PR further increases, it is seen that the difference between the starting positions of two leading shocks decreases.As PR increases to 3.9,the dominant separation region switches again with the shock train reaching the reflection point of S2,and then the back pressure begins to decrease. With the reduction of the back pressure, it is found that DS is still anchored at reflection point S2. As PR further decreases to 3.2,DS moves significantly downstream to anchor at point S4 while stepping across point S3.Unlike the uniform incoming flow, the non-uniform flow with complex background waves brings about a hysteresis in the location of the starting position of shock train. Fig. 20 shows the hysteresis loop diagram for the variation of length between the starting position of shock train and the position of S3. The length is represented by xS3(position S3)-xs(starting position of shock train), where negative value means the starting position of shock train is in the downstream of S3.

Fig. 17 Schematic of simplified model designed to contain background waves.

Fig. 18 Through flow field in isolator with background waves.

The switch phenomenon of DS has been observed in a previous study,11whilst the details were obtained in the present simulations. Fig. 21 shows the pressure distributions along the lower wall in PR rising process. At PR=3.2, the starting position of leading shock is downstream of the pressure plateau after the impingement of the background shock. At PR=3.3, the starting point almost reaches the leading edge of the pressure plateau, while the pressure at point S3 is still uninfluenced. As a matter of fact, the background shock will interact with the leading shock wave on S3 as long as the back pressure increases slightly beyond PR=3.3. Hence, the coupled action of the background shock and the leading shock results in a significant large-scale separation of the boundary layer on the lower wall, which triggers a mutation in starting position of shock train. As a result, the main flow turns towards the upper wall,and thus the previous DS on the upper wall is swept away. Consequently, DS reestablishes on the lower wall at PR=3.4,as shown in Fig.19.As the back pressure further rises, the same process would be reproduced at point S2. The above gives an explanation to the mechanism of the switch of DS.

Fig. 19 Mach number contour in hysteresis loop.

Fig. 20 Hysteresis loop of length between starting position of upstream shock train and point S3.

Fig. 21 Pressure distributions along lower wall in PR rising process under condition of background waves.

There are two remaining issues need to be addressed. The first is that the mechanism of hysteresis has not been properly set forth yet. Combining the present results with those from the Refs.11,14,37,we infer that if there is a region with strong adverse pressure gradient in the downstream moves towards and merges with another one in the upstream,a hysteresis phenomenon will occur when the two regions try to separate.The reason why the dominant separation region hangs on position S2 can be mainly attributed to this mechanism. This will be discussed in detail in the next section.

The second issue is why the dominant separation zone is anchored at position S4 instead of position S3 when PR decreases from 3.3 to 3.2. We suggest that the expansion fan plays a major role in this respect by extending the scope of the lag loop.In the PR dropping process,the starting position of the leading shock moves downstream within the expansion fan region, as illustrated in the right side of Fig. 19. Because the expansion fan accelerates the core flow, the Mach number gradually increases within the expansion fan along the streamwise direction. And thus, within the expansion fan, the foot part of the upper leading shock has a gradually increasing upstream Mach number as it moves downstream. According to the model established in Section 3 and the result indicated in Fig. 8, the deflection angle of the separated boundary layer will slightly decrease.Consequently,the upper peripheral leading shock angle decreases, while the wavefront Mach number remains unchanged as PR decreases, indicating that the peripheral leading shock weakens.The reduction of the leading shock strength means a reduction of pressure rise across the shock train. Therefore, the shock train can match the reduction of back pressure by changing the strength of the upper leading shock. As PR decreases to 3.2, this regulatory mechanism can no longer match the back pressure, thus the DS moves downstream. Thus the DS is anchored at point S4 instead of S3.The variations of upper peripheral leading shock angle are listed in Table 2.

4.3. Hysteresis caused by jet injection

Fuel or gas injection is a common technique adopted in the isolator. A dense array of injection holes or an injection slot may well lead to boundary layer separation in the upstream of injection location. To verify the inference proposed at the end of Section 4.2, a cross jet is introduced to generate a separation region of the great adverse pressure gradient upstream.A simplified model is designed as follows.The jet is located on the lower wall and the beginning of jet slot is 100 mm downstream of the isolator entrance. The jet speed is locally sonic and its static pressure satisfies pjet=6p1. Fig. 22 shows the flow patterns when a slot jet injects into the core flow. The inflow conditions are the same as the free stream conditions for the case with background waves except for the attack angle.

Fig.23 displays the Mach contours of the present case.The dominant separation region of the shock train is attached to the lower wall. At PR=2.6, the leading shock of shock train locates downstream the reattachment shock. As PR increases to 2.9,the leading shock steps across the jet slot driven by back pressure,and the separation region of shock train merges with the separation induced by jet flow.As a consequence,the back pressure coupled with the adverse pressure gradient produced by the jet enlarges remarkably the boundary layer separation zone and merges the separation shock with the leading shock.As PR drops from 3.0, the leading shock is anchored at the upstream of the jet slot until PR reduces to 2.6. This verifies our inference that if there is a region with strong adverse pressure gradient in the downstream which moves towards and merges with another one in the upstream, a hysteresis phenomenon will occur when two regions start to separate. The hysteresis loop represented by the relative location between the shock train starting position xsand the gas injection location xjis shown in Fig.24,where the negative value means that the starting position of shock train is downstream of the jet.

Fig. 25 further shows the pressure distributions along the lower wall,which are similar to those described in Section 4.2.When the back pressure increases, the leading shock moves gradually upstream because of the supersonic flow between the reattachment shock and the shock train. Once the leading shock interacts with the reattachment shock, the separation shock suddenly moves sharply forward because of the back pressure. When the back pressure decreases, it continues to affect the boundary layer separation upstream the jet,and thus the dominant separation region is hooked on the jet slot until the back pressure becomes sufficiently small.

4.4. Common characteristics of the three hysteresis phenomena

The common characteristics of the three hysteresis phenomena studied in the section are that they appear as the boundary layer separates. Two new kinds of boundary layer separation hysteresis were identified in the study. The first kind is in the deflection angle of the separated boundary layer and is induced by the hysteresis in the transition between shock reflection types. The increase in the boundary layer separation angle leads to the occurrence of reflection hysteresis that was not observed previously. Essentially, the wall suction brings a strong shock holding ability to the isolator so that the leading shocks can be stabilized at the slot and its angle can reach the dual-solution domain of shock interference.The second kind isa hysteresis characterized by the location of the starting point of shock train. The background shock and the separation shock generates an adverse pressure gradient region respectively inside the isolator. It was inferred that, if these two adverse pressure gradient region interacts and merges with each other, the hysteresis will occur when the two regions try to separate.

Table 2 Variations of upper peripheral leading shock angle with back pressure ratios in PR drop process.

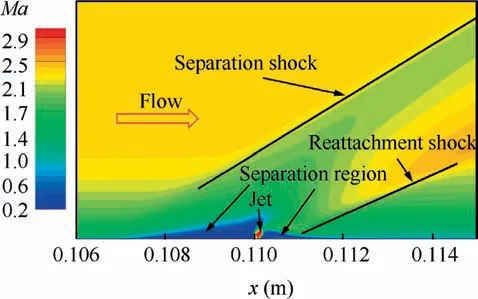
Fig. 22 Flow structures around jet slot.

Control theory indicates that hysteresis occurs when there is a mutation in the system. The transition from the regular to the Mach shock reflections is a mutation process, and thus a hysteresis takes place in the RR - MR transition. Similarly,the background shock wave, the jet, and the leading shock wave, which generate adverse pressure gradient regions in isolator flows, are all strong non-uniformity in supersonic flows.The interaction between the background shock wave, the separation shock wave and the separation region of shock train results in a sudden and large scale forward motion of the dominant separation region, as shown in Figs. 19, 20, and 23. It may well be the mutation that triggers a hysteresis.

Fig. 23 A hysteresis loop of Mach number contour for case of jet injection.

Fig.24 Hysteresis loop of length between jet location and shock train starting position.

Fig.25 Wall pressure distributions along lower wall in PR rising and decreasing process.

5. Conclusions For the complex flow inside the isolator, the present study numerically investigated the leading shock reflection patterns and the motion characteristics of shock train under both uniform and non-uniform incoming flow conditions. The nonuniform conditions are achieved by introducing different disturbances to the isolator, such as suction slot, background waves, and gas injection. The interactions between the shock train and the region with an adverse pressure gradient were studied in detail. The numerical results show that new kinds of hysteresis can take place in the deflection angle of separated angle and in the location of shock train.

For the uniform incoming flow conditions, based on a quantitative correlation purposed by Zukoski and the free interaction theory, a semi-empirical theoretical model was developed to predict the parameters of the leading shock of shock train. The model indicates that if the free stream Mach number is greater than 2.0, only regular reflection pattern can occur between the interference of two leading shocks.The hysteresis in the transition between MR and RR is impossible for the leading shocks of shock train.

With the boundary layer suction, background waves, and gas injection, the free interaction theory is no longer valid.When a suction slot was installed in the isolator,the hysteresis in transition between MR and RR was observed in the reciprocating variation of back pressure because of the significantly larger shock angles than those under uniform conditions.Furthermore, this hysteresis induces another new hysteresis phenomenon in the deflection angle of the separated boundary layer, which is proved by the coincidence of the same back pressure ratio range for both two kinds of hysteresis.

The shock train propagation under the effects of background waves is characterized by the switching process of the dominant separation zone.It is found that a substantial large-scale boundary layer separation appears once the leading shock moves upstream and interacts with the background shock.As a result,the dominant separation region switches towards the opposite wall. When the back pressure drops, a hysteresis occurs in the starting position of leading shock. The leading shock is anchored at the location where the background shock impinges the boundary layer until the leading shock recedes to the downstream shock impingement location on the same side.In the case with gas injection, the interactions between the separation region upstream the jet slot and the leading shock lead clearly to hysteresis in the starting location of the shock train.Its mechanism is suggested as that,when a downstream adverse pressure gradient region interacts and merges with an upstream one, a hysteresis will occur when the two regions start to separate.

Acknowledgments

This work is funded by the National Natural Science Foundation of China(Nos.11672309 and 11472279).The work in the Hong Kong Polytechnic University was supported by Central Research Grant (G-YBGA and G-YBXN).