Water takeoffperformance calculation method for amphibious aircraft based on digital virtual flight
2020-02-24LixinWANGHipengYINKunYANGHilingLIUJinghuiZHU
Lixin WANG, Hipeng YIN, Kun YANG, Hiling LIU,*, Jinghui ZHU
a School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China
b Chinese Flight Test Establishment, Xi’ an 710089, China
KEYWORDS Amphibious aircraft;Digital virtual flight;Hydrodynamic;Pilot model;Water takeoff performance
Abstract Owing to the strong coupling among the hydrodynamic forces, aerodynamic forces and motion of amphibious aircraft during the water takeoff process, the water takeoff performance is difficult to calculate accurately and quickly. Based on an analysis of the dynamics and kinematics characteristics of amphibious aircraft and the hydrodynamic theory of high-speed planing hulls, a suitable mathematical model is established for calculating the hydrodynamics of aircraft during water takeoff. A pilot model is designed to illustrate how pilots are affected by the lack of visual reference and the necessity to simultaneously control the pitch angle, flight velocity and other parameters during water takeoff. Combined with the aerodynamic model, engine thrust model and aircraft motion model,a digital virtual flight simulation model is developed for amphibious aircraft during water takeoff,and a calculation method for the water takeoff performance of amphibious aircraft is proposed based on digital virtual flight. Typical performance indicators, such as the liftoff time and liftoff distance,can be obtained via digital virtual flight calculations.A comparison of the measured flight test data and the calculation results shows that the calculation error is less than 10%, which verifies the correctness and accuracy of the proposed method. This method can be used for the preliminary evaluation of airworthiness compliance of amphibious aircraft design schemes,and the relevant calculation results can also provide a theoretical reference for the formulation of flight test plans for airworthiness certification.
1. Introduction
Amphibious aircraft are affected not only by aerodynamic forces, engine thrust and gravity but also by hydrodynamic forces during the water takeoff process. The motion parameters of aircraft, such as the pitch angle, draft and flight velocity, vary rapidly with time, and the variation of these parameters has a great influence on hydrodynamic and aerodynamic forces.1Obviously, there is a strong coupling among hydrodynamic forces,aerodynamic forces and aircraft motion.Complicated dynamics and kinematics characteristics make it difficult to accurately calculate hydrodynamic forces.2A landplane can usually be treated as a particle, without considering the attitude change of the aircraft, when the ground takeoff performance is calculated.3,4However, the fuselage of an amphibious aircraft transitions from submergence in water to separation from water during water takeoff, and the pitch angle of the aircraft will change greatly. The hydrodynamic and aerodynamic forces of amphibious aircraft are all related to flight attitude. Obviously, the particle flight performance calculation method of landplanes cannot represent the real dynamics and kinematics characteristics of amphibious aircraft during water takeoff process. Hence, this method is not suitable for calculating water takeoff performance. Moreover,pilots lack visual reference while taking off from water,and the interference of waves reduces a pilot’s ability to identify aircraft motion parameters.5,6According to the requirements of airworthiness,pilots also need to control the pitch angle,flight velocity and other parameters in real time.7Obviously, the operation of a pilot during water takeoff is quite different from that during ground takeoff, and these differences have a great influence on the takeoff performance. The above problems bring great difficulties to the calculation of the water takeoff performance of amphibious aircraft, and no systematic theoretical method for this calculation has been developed to date.8,9Consequently,a new calculation method of water takeoff performance needs to be proposed for amphibious aircraft,which can be used for airworthiness compliance pre-evaluation of the overall scheme at the conceptual design stage to avoid defects in flight performance and flight safety and can also be used to provide data support for the formulation of flight test plans for airworthiness certification.10,11
Very little published research has discussed the calculation method for the water takeoff performance of amphibious aircraft in recent years. Related works have mainly focused on the hydrodynamic estimation of seaplanes12,13and the stability evaluation of planing hulls14,15through towing tank experiments and Computational Fluid Dynamics (CFD) methods.16-19Although the experimental approach provides more accurate data, it also requires longer cycles and more funds.The CFD method involves dynamic mesh technology and two-phase flow solution, which increases the computing time and computational complexity needed.8,20Owing to the disadvantages above,an empirical method based on the test data of planing hulls can therefore be used for estimating takeoff performance, which is more suitable for the conceptual design stage.21Sun and Ma8proposed a resistance evaluation method for flying boats, including the effect of aerodynamic distribution, and they calculated the takeoff running distance of a small flying boat with the proposed method. Zhu22and Wu et al.23developed prediction methods for the water takeoff motion performance of a seaplane, respectively, based on different hydrodynamic estimation formulas of high-speed planing hulls.
However, semi-theoretical and semi-empirical formulas of high-speed planing hulls were used in the above studies for hydrodynamic calculation. In these approaches, the buoyancy and hydrodynamic lift are estimated as a quantity that cannot accurately calculate the buoyancy and buoyancy center position of aircraft. Unlike high-speed planing hulls, amphibious aircraft have wings, horizontal tails and vertical tails; hence,these aircraft have a large mass, a deep draft and a complex bottom shape.During the whole process of water takeoff,both the buoyancy and buoyancy center position vary greatly.Therefore,it is necessary to treat hydrodynamic lift and buoyancy as two independent variables to accurately calculate the changes in the buoyancy, buoyancy center, hydrodynamic lift and hydrodynamic pressure center of an aircraft. Then, the abovementioned studies assume that the aircraft is always in a stable planing state, ignoring the damping effect of water on the fuselage when hydrodynamic forces are calculated.22Consequently, the existing calculation methods are difficult to precisely describe the motion characteristics of amphibious aircraft during water takeoff.In addition,the influence of pilot operations on the takeoff performance of aircraft is not considered in the abovementioned methods.
This paper proposes a calculation method for the water takeoff performance of amphibious aircraft based on digital virtual flight.24,25First, mathematical models of buoyancy and hydrodynamic lift are established.The calculation method of the longitudinal hydrodynamic damping moment is proposed. Combined with the calculation method of hydrodynamic resistance and hydrodynamic pressure center, a mathematical model suitable for calculating the hydrodynamic forces of the amphibious aircraft is formed. Second, the amphibious aircraft water takeoff motion model is built by establishing a mathematical model of aerodynamic forces and engine thrust. Third, aimed at the problem that the pilot needs to control the pitch angle, flight velocity and other targets simultaneously and that the wave interference can reduce the pilot’s ability to identify the motion parameters of the aircraft, a pilot model suited for water takeoff is developed.Finally, a digital virtual flight simulation calculation model for the water takeoff is formed. The time-domain response of each motion parameter during the water takeoff process is obtained through the calculation for an amphibious aircraft,and typical takeoff performance indicators, such as the liftoff velocity and liftoff distance, can be determined. The calculation results are compared with flight test data, and the accuracy and reliability of the proposed method are verified.
2. Hydrodynamic model for water takeoff
The hydrodynamic forces acting on amphibious aircraft during water takeoff include buoyancy, hydrodynamic lift and hydrodynamic resistance. Based on the mechanics characteristics of the amphibious aircraft mentioned in the introduction,in this section, the mathematical models of the buoyancy,buoyancy center,hydrodynamic lift,hydrodynamic resistance,hydrodynamic pressure center and hydrodynamic damping moment of the aircraft are established by adaptively modifying the existing mechanics models from planing hulls, ships, and conventional landplanes.
2.1. Buoyancy and buoyancy center
During the water takeoff process of amphibious aircraft, the buoyancy decreases gradually with decreasing waterline height. Buoyancy Fbucan be calculated by Archimedes law as follows:

where ρwis the density of water, g is the acceleration of gravity, and Vpis the submerged volume of the aircraft fuselage.Assume that ρwand g are unchanged during takeoff, and the calculation of buoyancy can be converted to the calculation of the submerged volume of the aircraft fuselage Vp. The segmentation volume method is used to obtain Vpto guarantee the speed and accuracy of the calculation.26First, the fuselage is divided into 21 longitudinal sections with a spacing of Δx along the length direction of the fuselage, as shown in Fig. 1.
Second, the immersion area Aiof the ith longitudinal section is calculated based on the flight altitude, attitude angle and configuration data of the fuselage, as shown in Fig. 2.
Finally, the submerged volume AiΔx of each longitudinal section is calculated,and the submerged volume of the fuselage Vpcan be obtained by accumulating the submerged volume of all sections along the length direction of the fuselage by using the idea of numerical integration. The mathematical model of Vpcan be expressed as

According to the definition of the buoyancy center, the mathematical model of the longitudinal position of the buoyancy center xBcan be written as

where MYOZis the static moment of the submerged volume to the YOZ plane and xiis the x coordinate of the ith longitudinal section.
2.2. Hydrodynamic lift
Generally,the bottom of the fuselage is usually abstracted as a planing surface for force analysis when the amphibious aircraft is taxiing on the water.26Based on the studies of hydrodynamic loads on flat-bottom planing surfaces with high aspect ratio, the wetted length-beam ratio and the pitch angle are modified by combining the configuration features of the amphibious aircraft and the kinematic characteristics of the water takeoff process. The hydrodynamic lift mathematical model is obtained in this subsection.
According to Ref. 27, the hydrodynamic lift of the planing surface with high aspect ratio Lpscan be estimated by

where Vpsis the velocity of the planing surface,S is the wetted area,λ is the wetted length-beam ratio,and θ is the pitch angle.
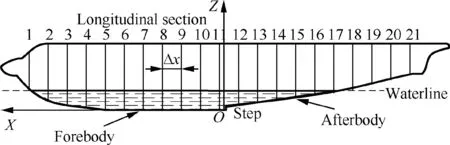
Fig.1 Longitudinal sections of an amphibious aircraft fuselage.

Fig. 2 Immersion area of a longitudinal section.
2.2.1. Modification of wetted length-beam ratio
When the planing surface is taxiing on water, waves rise in front of the surface, thereby causing the running wetted length-beam ratio λ1to be larger than the calm-water lengthbeam ratio λ, as shown in Fig. 3.
Based on Ref. 28, λ1can be calculated with the following empirical equations:
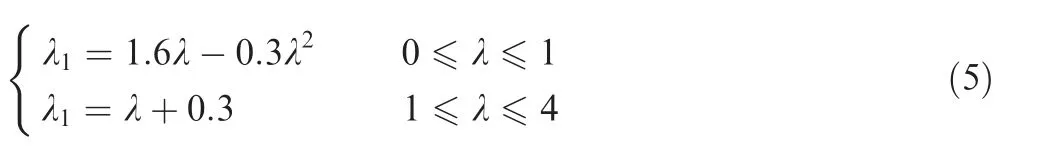
Furthermore,due to the deadrise angle at the bottom of the amphibious aircraft fuselage shown in Fig.2,the configuration of the amphibious aircraft is different from a planing surface.Consequently, the wetted length-beam ratio needs to be modified according to the deadrise angle with the following equation:

where ξ is the distance from the center of gravity to the step,B is the beam of the planning surface, and FrBis the width Froude number.27
After the modification of the wetted length-beam ratio, the wetted area of the amphibious aircraft can be obtained by

2.2.2. Modification of pitch angle
Unlike a planing surface, the bow of an amphibious aircraft bends upward, and the lift surface corresponds to a curved planing surface,as shown in Fig.1.The actual angle of attack of the bow is larger when the front intersection of the waterline and keel is in the curved section of the keel line.29Hence, the pitch angle needs to be modified as where θbis the modified pitch angle,Lsis the wetted length of the forebody keel, Lbis the length of the straight line segment of the forebody keel, and kbis the modification coefficient,which is related to the form of the bow.
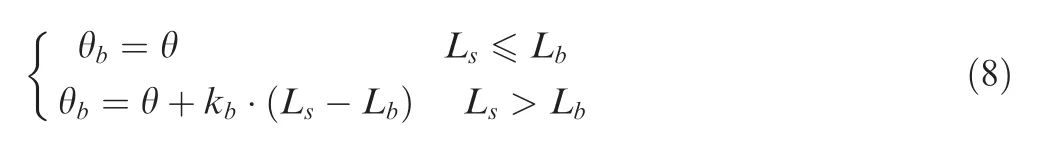
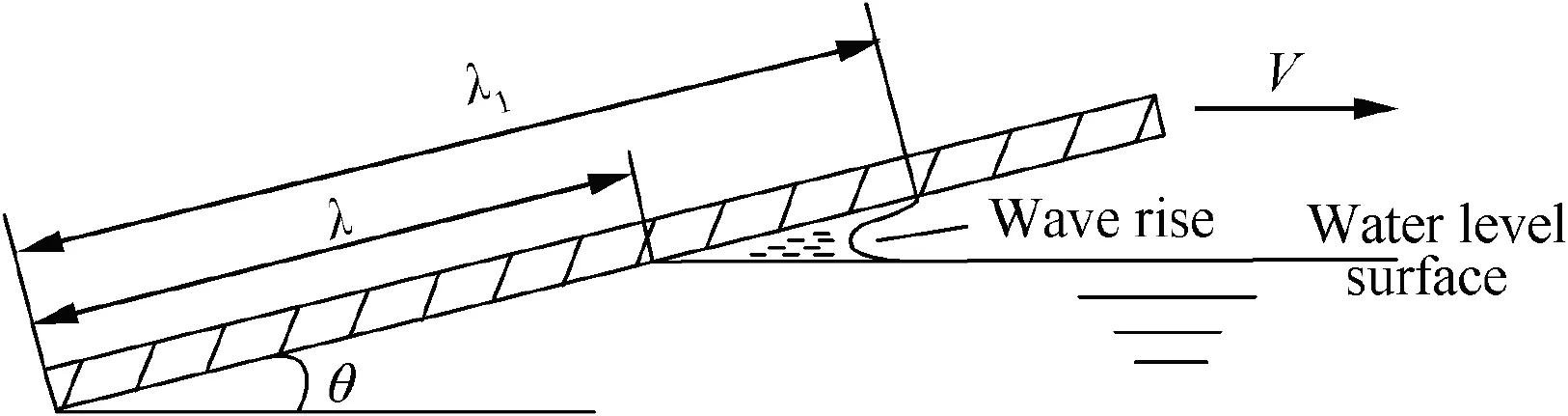
Fig. 3 Wave rise on a flat planing surface.
Moreover, the influence of the deadrise angle of the amphibious aircraft also needs to be considered when the pitch angle is modified. Through towing tank experiments of a scaled ship model,the modification approach can be expressed by the following empirical formula:27

Combining Eqs. (4), (6), (7) and (9), the mathematical model of hydrodynamic lift for amphibious aircraft during the water takeoff process is obtained as

where V is the flight velocity.
2.3. Hydrodynamic resistance
Based on Froude’s theory, the hydrodynamic resistance of ships can be divided into three parts: frictional resistance, viscous pressure resistance and wave resistance.20Compared to general ships, amphibious aircraft can produce heavy spray on both sides of the fuselage during the water takeoff process.Spray resistance is also an important component of hydrodynamic resistance. Therefore, the hydrodynamic resistance of amphibious aircraft is the sum of frictional resistance, viscous pressure resistance, wave resistance and spray resistance,26which is expressed as

In this formula,Rf,Rvpand Rwacan be converted to calculate the corresponding resistance coefficients Cf, Cvpand Cwa.
For the frictional resistance coefficient Cf, the 1957-ITTC equation30is used, which is given as

where Re is the Reynolds number.
For the viscous pressure resistance coefficient Cvp, the experimental results show that the ratio of the viscous pressure resistance coefficient Cvpto the friction resistance coefficient Cfis a constant k:

where k is called the shape coefficient, which is related to the shape of the fuselage.20
For a given amphibious aircraft,the wave resistance coefficient Cwaunder different Froude numbers can be calculated by the Michell integration method:31

For the calculation method of the spray resistance of amphibious aircraft, one can refer to the empirical formulas of planing hulls. Based on the calculation formula of the area wetted by spray Aasobtained from relevant experiments, the mathematical model of the spray resistance Rscan be established as

where Cfsis the friction coefficient,which is calculated according to the Reynolds number of the spray areas.32
2.4. Hydrodynamic pressure center
Experimental studies of the hydrodynamic pressure center of the planing surface demonstrated that the distance from the pressure center to the stern is related to the wetted length,which is expressed as27

where lpis the distance from the pressure center to the stern and l is the wetted length of the planing surface.
For the amphibious aircraft, the hydrodynamic forces are mainly generated by the forebody of the fuselage.22Therefore,while Eq.(16)is used to calculate the position of the hydrodynamic pressure center, l is taken as the mean wetted length of the fuselage,29and lpis calculated as the distance from the hydrodynamic pressure center to the step. Combined with the data of the keel, the longitudinal and vertical positions of the hydrodynamic pressure center can be calculated.
2.5. Hydrodynamic damping moment
The parameters of planing hulls, such as the draft and wetted area,change slightly during planing.The hydrodynamic damping moment is not considered in the existing hydrodynamic calculation methods. However, these parameters change rapidly during water takeoff, and the damping effect of water on aircraft motion cannot be ignored.22Therefore, a formula for quantifying the longitudinal hydrodynamic damping moment is developed in this subsection based on the approach of calculating the aerodynamic damping moment of aircraft,thereby filling the void in traditional hydrodynamic analysis methods.
The longitudinal aerodynamic damping moment of a general aircraft Mqcan be expressed as

where Cmqis the longitudinal aerodynamic damping coefficient, ρ is the air density, Sais the wing area, c is the length of the mean aerodynamic chord, and q is the pitch rate.33
The mechanism of the hydrodynamic damping moment is similar to that of the aerodynamic damping moment. Therefore, the mathematical model of the hydrodynamic pitch damping moment Mqwis obtained by replacing ρ with ρw, Sawith Swand c with l in Eq. (17):

where Cmqwis the longitudinal hydrodynamic damping coefficient.
3. Amphibious aircraft motion model
The motion of amphibious aircraft is affected by hydrodynamic forces, aerodynamic forces, engine thrust and gravity during the water takeoff process.Therefore,the motion model of amphibious aircraft can be obtained by adding buoyancy Fbu, hydrodynamic lift Lw, hydrodynamic resistance Rw,hydrodynamic moment Mwand hydrodynamic damping moment Mqwto the general longitudinal dynamic equation:33

where m is the mass of the aircraft; Ix, Iyand Izare the moments of inertia; Izxis the product of inertia; u, v and w are the scalar components of the airspeed; p and r are the roll rate and yaw rate, respectively; Dband Lbare the scalar components of the aerodynamic force in the body axes; Mais the aerodynamic pitching moment; FTxand FTzare the scalar components of the engine thrust in the body axes; MTis the pitching moment of the engine. This model accurately describes the force condition of an amphibious aircraft during water takeoff and can be used in many fields, such as the calculation of flight performance, the calculation of stability and maneuverability, and the evaluation of airworthiness compliance.
When the aircraft leaves the water,the hydrodynamic terms in Eq. (19), including buoyancy, hydrodynamic lift, hydrodynamic resistance, hydrodynamic moment and hydrodynamic damping moment, are all reduced to 0, and the model will be simplified as the longitudinal motion model of aerial flight.
3.1. Aerodynamic model
The formulas for calculating the aerodynamic forces and moments of amphibious aircraft during the water takeoff process are

where L and D are the aerodynamic lift and resistance,respectively, CLand CDare the aerodynamic coefficients, and Cmis the aerodynamic moment coefficient. The aerodynamic coefficients and aerodynamic moment coefficient are obtained from wind tunnel tests, which are composed of basic terms, control surface increment terms,dynamic derivative terms and ground effect modification terms:

Since the amphibious aircraft taxis at the interface of air and water, the calculation of aerodynamic and hydrodynamic forces is a transient two-phase flow problem. However, it is difficult to accurately estimate the influence between aerodynamic and hydrodynamic forces.The aerodynamic and hydrodynamic models are established separately in current research.According to Ref.2,this approach can obtain sufficient calculation accuracy.
In the water takeoff process, the aerodynamic force of the amphibious aircraft is smaller than the hydrodynamic force when the flight velocity is low. As the flight velocity increases,the hydrodynamic force decreases, and the aerodynamic force increases rapidly with the decrease of the draft of aircraft.After leaving the water,the aircraft flies according to the aerodynamic force, engine thrust and gravity.
3.2. Hydrodynamic model
The hydrodynamic forces in the motion model include buoyancy Fbu, hydrodynamic lift Lwand hydrodynamic resistance Rw, which are calculated using Eqs. (1), (10) and (11),respectively.
The hydrodynamic moment in the motion model includes the hydrodynamic moment Mwand the hydrodynamic damping moment Mqw.The hydrodynamic moment Mwis obtained by adding the moment generated by the buoyancy Fbu, the hydrodynamic lift Lwand the hydrodynamic drag Rw, and the corresponding mathematical model is expressed as
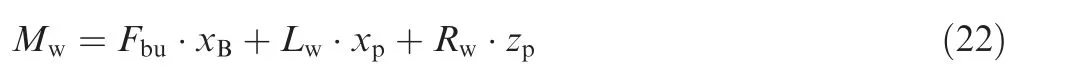
where xBis the position of the buoyancy center, which is calculated with Eq. (3), and xpand zpare the longitudinal and vertical distances from the hydrodynamic pressure center to the center of gravity,respectively,which are calculated according to the hydrodynamic pressure center model and the position of the center of gravity. The hydrodynamic pitch damping moment Mqwis calculated by Eq. (18).
When the flight velocity is low,the gravity of the aircraft is mainly balanced by buoyancy. As the flight velocity gradually increases, the hydrodynamic lift and hydrodynamic resistance acting on the fuselage gradually increase, the draft of the aircraft gradually decreases, the buoyancy decreases, and the gravity of the aircraft is mainly balanced by the hydrodynamic lift. With the further increase of the flight velocity, the hydrodynamic components are reduced due to the reduction of the wetted area. The hydrodynamic forces are reduced to 0 after the aircraft leaves the water.
3.3. Engine thrust model
During the water takeoff process,the pilot gradually increases the throttle until the engine reaches the peak conditions. The aircraft remains in this state until it leaves the water. The formulas for calculating the thrust and moment generated by the engines are
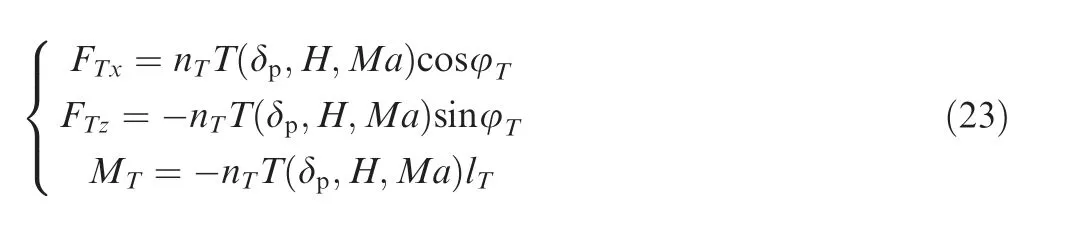
where nTis the number of working engines;T is the thrust of a single engine, which is a function of the throttle δp, flight attitude H,and Mach number Ma;φTis the mounting angle of the engine;lTis the distance between the center of gravity and the thrust line.
To simulate the response characteristics of the engine, the relationship between the actual throttle δpand the command of throttle δpcis shown as

where τpis the time constant of the engine, which affects the response characteristics of the engine, and s is the complex variable in the transfer function.
4. Pilot model for water takeoff
The pilot model is a mathematical model describing the human pilot’s operational behavior to the aircraft,which gives specific control input according to the current flight mission requirements and the flight state of the aircraft. Unlike ground takeoff, the pilot lacks visual references during water takeoff, and the waves can interfere with the motion of the aircraft and the pilot’s vision, which makes it more difficult for pilots to identify the motion parameters of the aircraft and reduces their perception of the motion state. Moreover, the pilot needs to control multiple targets simultaneously: the pilot not only needs to adjust the elevator in real time to ensure that the pitch angle is within the stable boundary and avoid causing longitudinal unstable motion but also needs to control the flight velocity and roll angle to avoid the heavy spray or the contact between the float and the water. These differences affect the pilot’s operational behavior and subsequently affect the water takeoff performance of the aircraft.
Aimed at the abovementioned features, a pilot model suitable for amphibious aircraft during water takeoff is established to complete the closed-loop simulation based on the multi-axis tasks pilot model theory proposed by Hess and Marchesi.34The interference of the above factors on pilot operations is characterized by the design of a visual cue model and gain reduction factor. The structure of the pilot model is shown in Fig. 4.
In Fig.4,θris the pitch angle reference command,which is designed according to the porpoising stability limit of the aircraft; Vris the velocity reference command, which is designed based on the velocity characteristics needed to be simulated during the water takeoff process; V(θ), V(q) and V(V) are the visual cue models of the pitch angle, pitch rate and flight velocity,respectively,which are used to characterize the reduction in pilot’s perception of flight state parameters;Kθ,Kqand KVare the control gains, and the selection approach of the pilot model gains can be found in Ref. 35; f is the gain reduction factor, which represents the decline in a pilot’s control gain caused by multi-axis control tasks and environmental interference; Gnrepresents a simplified model of the pilot’s neuromotor dynamics in the limb, which can be expressed as a second-order system with a natural frequency of 10 rad/s and a damping ratio of 0.707.

Fig. 4 Structure of pilot model for water takeoff.

4.1. Visual cue model
Under different wave conditions, a pilot’s ability to identify aircraft motion parameters will change accordingly. The higher the wave level, the greater the error in the visual information acquired by the pilot. Therefore, a visual cue model needs to be applied to the pilot model,and the structure of this model is shown in Fig. 5.
The visual cue model is intended to simulate the errors caused by the human pilot in acquiring visual signals by introducing random numbers. The random number generated in Fig. 5 is subject to a zero-mean Gaussian distribution with a variance of the parameter dvarv.The quality of the visual cues is quantified by the value of dvarv. The larger the value, the worse the visual cue. For amphibious aircraft, the value of dvarvis mainly affected by sea waves, which need to be selected according to the sea wave conditions. The saturation limits in the visual cue model are set to twice the variance of the zero mean,which can filter out unreasonable random numbers.A low-pass filter is used to filter the high-frequency component of the signal to avoid unreasonable high-frequency pilot control input.
4.2. Gain reduction factor
During water takeoff, pilots need to simultaneously control multiple targets,such as the pitch angle,flight velocity and roll angle, which distracts the pilot’s attention and decreases the pilot’s control gains. In addition, this simultaneous control also affects a pilot’s perception of flight states and eventually leads to poor control effects.
Research done by Hess indicates that multi-axis tracking induces increased human pilot remnant and decreased pilot control gain.35Therefore,the gain reduction factor f is defined as

where n is the number of channels being controlled.
For the water takeoff process, the longitudinal control is the main control objective; however, the slipstream of the engine induces a wash flow on the wing. Moreover, wind and waves usually occur in actual flight. Therefore, the lateral axes of the amphibious aircraft need to be controlled simultaneously to guarantee lateral stability,and the independent control channels include throttle,pitch,roll and yaw;n is taken as 4 in Eq. (26).

Fig. 5 Structure of visual cue model.
The establishment of a visual cue model and a gain reduction factor affects the pilot’s operator dynamics in three aspects:it increases the time delay of the pilot’s input,reduces the open-loop crossover frequency of the pilot-aircraft system,and increases the error-injected remnant.35Compared with the other kinds of pilot models,such as the McRuer model and the optimal control model, the established pilot model can reflect the characteristics of multi-objective pursuit control, and the parameters of the model can be adjusted according to wave condition,which is suitable for simulating a pilot’s operational behavior of an amphibious aircraft during water takeoff.
In the water takeoff process, the dynamic pressure is small when the flight velocity is low, and the moment generated by the control surface is limited.Hence, the pilot’s ability to control the aircraft attitude is also limited; As the flight velocity increases gradually, the deflection of the control surface will have a greater impact on the aircraft attitude and then affect the flight performance calculation results.
5. Comparison of calculated and experimental results
Through the proposed method, the hydrodynamic, aerodynamic, engine thrust, aircraft motion and pilot models are established to form the water takeoff digital virtual flight simulation model by using the data of the towing tank experiments, wind tunnel test, engine thrust and configuration from a typical amphibious aircraft.Fig.6 illustrates the overall structure of the simulation model.The elevator actuator is represented by a first-order inertia link with a time constant τe.Because the flight control system was not installed during the test flight,the mathematical model of the flight control system was not established in this paper.
The flight test was conducted under glassy water and calm wind conditions.Initially,the aircraft was taxiing on the water at a velocity of 8.1 m/s and a pitch angle of 3.7°. The flaps remained unchanged at 20° during the whole takeoff process.
The calculation results of flight velocity,flight altitude,taxiing distance, pitch angle, pitch rate, load factor, elevator and throttle are compared with the flight test data, as shown in Fig. 7. In the calculation results, the liftoff time is the time when the wetted length-beam ratio of the amphibious aircraft is equal to 0.
(1) Flight altitude and flight velocity
The water takeoff process can be divided into two phases:the planing phase and the climbing phase. In the planing phase, the velocity of the aircraft increases rapidly, and the altitude increases slightly. In the flight test, the aircraft leaves the water at 33.1 s,and the liftoff velocity is 49.8 m/s.The calculation results show that the liftoff time is 32.6 s and the liftoff velocity is 50.7 m/s.

Fig. 6 Structure of digital virtual flight simulation model.
In the climbing phase, the flight altitude increases rapidly,and the velocity increases slightly. In the flight test, the flight time to the screen height (15.24 m) is 38.4 s,3and the flight velocity is 55.1 m/s at this time. The calculation results show that the time to the screen height is 37.6 s,and the flight velocity at this time is 56.7 m/s.
Obviously, the calculation results of flight altitude and velocity are in good agreement with the flight test data,indicating that the digital virtual flight method can reproduce the variation characteristics of flight altitude and velocity during water takeoff.
(2) Liftoff distance
The liftoff distance in the flight test is 709 m,and the liftoff distance calculated by the digital virtual flight simulation is 690 m; this 19 m difference corresponds to a relative error of 2.7% in the calculation.
(3) Pitch angle and pitch rate
As power is applied, the increasing velocity generates an increasing hydrodynamic lift, and the nose-up moment produced by the hydrodynamic lift increases gradually because the hydrodynamic pressure center is in front of the center of gravity. Therefore, the pitch angle of the aircraft increases until reaching a peak value. In the vicinity of the peak of the pitch angle, the hydrodynamic resistance reaches the maximum value in the whole takeoff process, which is referred to as the hump.5In the flight test,the peak time of the pitch angle is 17.9 s,the peak value of the pitch angle is 7.5°and the maximum pitch rate is 2.7 (°)/s. Through the digital virtual flight simulation calculation, the peak time of the pitch angle is 18.1 s, the peak value of the pitch angle is 7.6°, and the maximum pitch rate is 2.3 (°)/s.
After passing over the hump, the planing area of the aircraft forebody decreases as the draft is further reduced. The hydrodynamic pressure center shifts back, and the nose-up moment generated by the hydrodynamic forces decreases.Meanwhile, the hydrodynamic resistance also produces a nose-down moment. Hence, the pitch angle decreases gradually until the aircraft leaves the water. In the flight test, the pitch angle is 4.2° when the aircraft becomes airborne, and the simulation result is 3.8°.
Fig. 7 (d) and (e) show that the pitch angle and pitch rate responses calculated by the digital virtual flight method can accurately reproduce the unique motion characteristics during water takeoff, which are different from those during ground takeoff.
(4) Load factor
From 0 s to 18 s, the pilot gradually increases the throttle,and the tangential load factor gradually increases from 0.12 to 0.28,which indicates the acceleration of the amphibious aircraft.The tangential load factor reaches the maximum value of 0.28 at 18.1 s in the flight test.The maximum value of the tangential load factor in the simulation is 0.27 at 17.9 s. After passing over the hump,the thrust of the engine reaches a maximum value and remains unchanged, and the tangential overload obtained from the flight test and calculation is basically unchanged. After 30 s in the flight test and calculation results,the engine thrust decreases slightly with increasing flight velocity. As a result, the tangential overload decreases slowly.

Fig. 7 Comparison of time-domain responses of motion parameters between calculation and experiment.
The normal load factor varies slightly in the first 15 s, and there is a peak at the hump speed. The normal load factor obtained from the flight test decreases to 0.86 at 18 s, and the calculated result decreases to 0.89 at 18 s. After passing over the hump, the normal load factor stabilizes to approximately 1.
Obviously, the overload obtained by the digital virtual flight simulation can reproduce the variation characteristics of overload during water takeoff.
(5) Operations
From 0 s to 10 s in the water takeoff process,the pilot gradually increases the throttle and slightly pushes forward the control stick to make the aircraft accelerate smoothly and avoid the additional resistance produced by excessive pitch angle. From 10 s to 15 s, the pilot pulls aft control stick. In the flight test, the elevator angle increases from 2.5° to 10.5°.In the simulated responses, the elevator angle increases from 2.15° to 10°. In this phase, the pitch angle of the aircraft increases rapidly.
Between 15 s and 20 s, the peak of the pitch angle appears,and the pilot properly pushes forward the control stick to avoid the porpoising caused by excessive pitch angle. After 20 s, the elevator angle is adjusted according to the required planing attitude.
After the amphibious aircraft leaves the water at 33 s, the pilot reduces the elevator angle to establish the pitch attitude for the best rate of climb. In the flight test, the elevator angle decreases from 9° to 0°, and in the simulation, the elevator angle decreases from 8° to 0°.
In the flight test data and calculation results, the throttle response gradually increases from ground idling to the peak conditions at 25 s and then remains unchanged. Afterwards,the throttle decreases to 80%when the aircraft leaves the water at 37 s.
Fig. 7 (h) and (i) compare the flight test data and simulation results of the elevator and the throttle during water takeoff process. Obviously, the calculation results are in good agreement with the flight test data, which reproduce the pilot’s operational behavior during the whole takeoff process.
The calculation results of the typical water takeoff performance indicators are compared with the flight test results, as shown in Table 1.
Obviously, the calculation results are in good agreement with the flight test data, and the corresponding error is within 10% for all performance indicators.
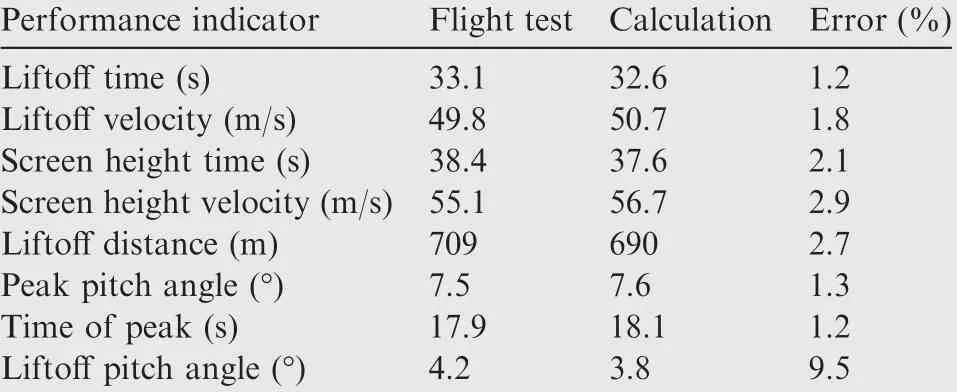
Table 1 Comparison of calculation results and flight test data.
6. Conclusions
(1) By establishing the buoyancy and hydrodynamic lift model separately, the accuracy of the longitudinal hydrodynamic calculation is improved. A formula for calculating the hydrodynamic damping moment is developed, which solves the problem of ignoring the damping effect of water in the traditional methods. A pilot model suitable for calculating water takeoff performance is built to illustrate the effect of multiobjective pursuit control, lack of visual reference and wave interference. A method for calculating the water takeoff performance based on digital virtual flight is proposed.
(2) The time-domain calculation results and flight test data of motion parameters(such as the pitch angle and flight velocity) during the water takeoff process are compared and analyzed. The results show that the calculated results of typical motion characteristics (such as the peak value of pitch angle and the time of peak) are in good agreement with the flight test data. Therefore,the calculated results can accurately reproduce the motion characteristics of amphibious aircraft during water takeoff.
(3) A comparison of the calculation results of typical takeoff performance indicators in the water takeoff process and the flight test data shows that the calculation errors of each parameter are below 10%,which shows that the method proposed in this paper can objectively and accurately calculate water takeoff performance.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Design and experimental study of a new flapping wing rotor micro aerial vehicle
- CFD/CSD-based flutter prediction method for experimental models in a transonic wind tunnel with porous wall
- Prediction of pilot workload in helicopter landing after one engine failure
- Study of riblet drag reduction for an infinite span wing with different sweep angles
- Modulation of driving signals in flow control over an airfoil with synthetic jet
- Strong interactions of incident shock wave with boundary layer along compression corner
