A review on carrier aircraft dispatch path planning and control on deck

Xinwi WANG, Ji LIU, Xicho SU, Hijun PENG, Xuong ZHAO,Chn LU

a Department of Engineering Mechanics, State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China

b Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China

c War Research Institute, Academy of Military Sciences, Beijing 100850, China

d Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China

e School of Reliability and Systems Engineering, Beihang University, Beijing 100083, China

KEYWORDS Carrier aircraft;Dispatch;Kinematic model;Path planning;Path tracking

Abstract As an important part in sortie/recovery process,the dispatch of carrier aircraft not only affects the sortie/recovery efficiency and safety,but also has severe influence on the carrier’s combat efficiency and the comprehensive support capability. Path planning is the key to improve the efficiency and safety during the dispatch process.The main purpose of this paper is to propose a comprehensive investigation of techniques and research progress for the carrier aircraft’s dispatch path planning on the deck. Three different dispatch modes of carrier aircraft and the corresponding modeling technologies are investigated, and the aircraft’s dispatch path planning techniques and algorithms have been classified into different classes. Moreover, their assumptions and drawbacks have been discussed for single aircraft and multiple aircraft.To make the research work more comprehensive,the corresponding tracking control methodologies are also discussed.Finally,due to the similarity of path planning problem between the carrier aircraft’s dispatch and those in other fields,this paper provides an exploratory prospect of the knowledge or method learned from other fields.©2020 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

As an important symbol of national power,the aircraft carrier plays an irreplaceable role in maritime security and interests,1,2and carrier aircraft is the main combat weapon on it. In the future, the number of aircraft carried by the carrier platform will gradually increase. In addition, as the training/ combat intensity increases, the activity of carrier aircraft will become more and more frequent on the deck.The combat efficiency of the entire aircraft carrier group largely depends on the sortie of carrier aircraft, where dispatch is one of the key parts of it.3,4

Compared with land-based aircraft operations,the space of the deck is much narrower.5It is necessary to carry out many operations (as shown in Fig. 1) such as take-off, landing, and support,all with a dispatch space of 4.5 acres.6,7However,the aircraft carrier deck is a completely open space, there is no fixed runway as land-based dispatch, and all idle parts of the deck can be used as a runway. Hence, the dispatch path planning on the deck is more complicated than land-based aircraft operations. There is a high risk in the transfer process of the carrier aircraft on the deck. The flight deck incidents officially recorded by the U.S. navy include many serious injuries and deaths, as well as many instances of aircraft damage or loss.According to accident reports from the Naval Safety Center,there were 3228 related incidents from 1980 to 2008,and more than 30% of those happened in dispatch processes.8Dispatch accidents not only cause significant economic loss, more importantly, but also affect the carrier’s combat capability.A collision between two aircraft on the flight deck may disrupt maintenance and support plans for other aircraft, increasing the logistical pressure.And accident could lead to mission failure, whose impact may last for days or weeks. It can be concluded that a reasonable dispatch scheme is of great significance to ensure the operation safety of the carrier aircraft on the deck.

The current methods to realize the dispatch for carrier aircraft much depend on artificial expertise, which is feasible when the number of aircraft is relatively small.9However,when the number of dispatched aircraft is large, it is difficult to plan a scientific and reasonable dispatch scheme based on manual experience. As a result, unreasonable dispatch plans will be obtained in scenarios such as nights or other poor meteorological conditions.10In addition, Unmanned Aerial Vehicles (UAVs) have been gradually applied in the military field.With the unique advantages, carrier UAVs will be used based on the aircraft carrier platform in the future.3,11,12Unlike manned carrier aircraft, UAVs usually taxi by themselves,and it is true that the dispatch of UAVs is more automated than that of manned carrier aircraft. Therefore, the research on carrier aircraft automatic transport planning and control technology can provide relevant technical reference for the carrier UAVs.

There is rich review literature on path planning of vehicles in other fields, such as mobile robots,13,14UAVs,15autonomous self-driving vehicles,16,17and Autonomous Underwater Vehicles (AUVs).18Similar to the path planning problem of other vehicles, in the process of dispatch, a collision-free taxiing path that connects the initial parking position and the destination is expected. And the generated path should be as smooth as possible while satisfying various constraints on state and control inputs.However,the dispatch path planning problem of carrier aircraft on the deck has distinct features. The most notable one is that there is a high precision demand on the terminal posture to ensure success of the following catapult and launch operation.As for the fleet launch process,the maximum allowable number of carrier aircraft taxiing simultaneously equals the number of catapult equipped on the flight deck. And there might be constraints on launch priority for aircraft of different types due to the requirement of the certain mission. Last but not the least, considering that there is unavoidable base motion of the carrier under the effect of wind and wave loads, larger safety margins must be set in the path planning problem.

Having a good command of the dispatch process and dispatch modes, as well as the operational environment on the flight deck and constraints encountered, is the prerequisite to design high-quality dispatch paths.The dispatch path planning can be generally divided into path planning and control for single aircraft and coordinated path planning and control for multiple aircraft. There is few research of aircraft dispatch path planning problems or related model analysis.The existing research generally focuses on taxiing path planning for single aircraft, and various constraints are not taken into consideration. Hence, the obtained taxiing path is hardly directly applied in practice. Besides, there is almost no relevant literature of the path tracking for the towed aircraft system with/without drawbar, and there is almost no concise and applicable kinematic or dynamic model. In the process of fleet dispatching, coordinated dispatch path planning is very common and important. However, studies on the path planning of multiple aircraft are rarely seen. Therefore, it’s meaningful to establish the corresponding kinematic and dynamic model according to different dispatch modes, and generate optimal path and control command that satisfy all necessary constraints so that the results can be directly applied to the practical dispatch processes. However, to the best of our knowledge, there is no literature that summarizes the techniques for carrier aircraft dispatch path planning and control on deck till now.Hence,this review will provide a comprehensive and broad view on every detail in the dispatch path planning and control on deck at length.

Fig. 1 An illustration of take-off and landing process on the deck.4

The remainder of the paper is organized as follows. An overview of the dispatch of carrier aircraft on the deck is given in Section 2. The kinematic model in three different dispatch modes are investigated and compared in Section 3.In Section 4,the path planning techniques for single carrier aircraft are reviewed. In Section 5, the coordinated path planning techniques for multiple carrier aircraft are reviewed. In Section 6,a review of trajectory tracking techniques used in the dispatch of carrier aircraft is given.In Section 7,several possible future research directions of this field are provided. Section 8 concludes the paper.

2. An overview of the dispatch of carrier aircraft on the deck

2.1. Dispatch process in sortie and recovery task for carrier aircraft

As illustrated in Fig. 2, the sortie process can be roughly described as follows: Once the sortie task order is given, the corresponding aircraft will be dispatched from the hangar to the elevator with tractor.Next,the elevator will lift the aircraft from the hangar to flight deck, and the aircraft will be dispatched from the elevator to the corresponding gate position with tractor. Then, the aircraft will taxi to the corresponding catapult from the gate position for ejection until the corresponding supply and check work have been done. When the combat mission is completed, the aircraft lands on the flight deck and returns to the hangar, where the recovery process(the aircraft return to the hangar) is roughly the reverse of the sortie process. The dispatch efficiency and satisfaction of collision-free conditions and other constraints are the core issue in the corresponding path planning.

It is seen that the aircraft dispatch takes large parts in the sortie and recovery process. The transfer from the hangar to the flight deck(or from the flight deck to the hangar)by elevator is fixed, and the corresponding dispatch path is fixed too.Hence, the dispatch path planning in this stage is not considered in this paper.

2.2. Three dispatch modes and corresponding application scenarios

It is necessary for us to compare current dispatch modes and the corresponding application scenarios before conducting the research of path planning and control.It helps us to understand the dispatch environment and the path planning model according to certain transport scenarios and tasks so that we can obtain accurate and practical results.

The dispatch of carrier aircraft on the deck is mainly divided into three modes:(A)autonomous taxiing(i.e.,taxiing by the aircraft itself without a towing vehicle), (B) towed aircraft system without a drawbar,and(C)towed aircraft system with a drawbar.Generally,the first and third types are mainly used for aircraft dispatch on the flight deck, and the second type is mainly used for aircraft dispatch in the hangar.A brief comparison of the three dispatch modes is given in Table 1.As the configurations of such three modes are different,their kinematics and control characteristics vary from each other.Hence,it is meaningful to study the kinematics of three different dispatch systems.

In towed modes, the tractor provides the power of the whole system. And it has three advantages over autonomous taxiing mode.First,it saves the fuel of the aircraft on the deck and thus improves the endurance capacity of the aircraft. Second, it avoids the engine of the aircraft switching frequently between the on and the off state, improving lifetime of the engine. Last but not the least, reversing motion of the aircraft can be implemented, improving the flexibility of dispatch.

2.3. Analogy of path planning between aircraft dispatch and unmanned ground systems

Based on the above introduction, it’s found that the motion characteristics of three dispatch modes have much in common with those of some Unmanned Ground Systems (UGSs). For aircraft taxiing by itself, front wheels provide the acceleration and the steering operation is controlled by the nose wheel,which is alike to automobiles. The classical bicycle model widely used in trajectory planning for autonomous driving is applicable to describe the motion of the carrier aircraft on the deck. However, the autonomous taxiing aircraft cannot realize backward motion by itself. As for towed aircraft systems (with/without a drawbar), their configurations are very similar to tractor-trailer systems where the tractor provides the power of the whole system. Similar to tractor-trailer systems, the reversing motion is inherently unstable and the control during this operation needs special care.

Fig. 2 An illustration of dispatch process in sortie and recovery task for carrier aircraft.

Table 1 Three dispatch modes and typical application scenarios.

The research on path planning of UGSs is more extensive than that of carrier aircraft,and some good ideas and methods in these fields can be used as reference. Meanwhile, the path planning problem of carrier aircraft on the deck has its unique characteristics.Therefore,a brief comment is made on the differences between carrier aircraft and these UGSs in path planning.

Generally speaking, the tractor-trailer systems or chained robots usually focus on the whole system,19-22and they seldom need to strictly satisfy a certain fixed terminal constraint (i.e.,there is rarely such a scenario or requirement that they need to be dispatched to a certain position accurately with a certain orientation). So, they have a higher tolerance to satisfy the condition of terminal constraints. However, the purpose of towed aircraft systems (with/without drawbar) is to dispatch the aircraft to the prescribed destination with a fixed terminal orientation,and the tractor will not get too much attention.As the deck space resources are so valuable and many supporting facilities are fixed in the corresponding location, the aircraft need to strictly satisfy certain prescribed terminal constraints.Therefore, compared to the tractor-trailer systems or chained robots, the obstacles are denser.

Another difference between autonomous taxiing aircraft and UGSs or robots mainly reflects in the collaborative path planning problem. For the collaborative path planning of UGSs or robots, the initial or terminal time is identical for all agents, and each agent has a different terminal position.However, the problem of coordinated taxi path planning for carrier aircraft is very special. As the limited number of catapults, the path planning of carrier aircraft is coupled with the mission planning of sortie. If the number of aircraft involved in one sortie mission is bigger than the number of catapults, at least two aircraft would share one catapult, which suggests that at least two aircraft would share the same terminal position. As a result, mission planning must be considered to avoid conflicts rather than only path planning. Besides, the starting time and arrival time of each aircraft can be different,and each aircraft should strictly meet the corresponding terminal constraints. This puts forward higher requirements for the collaborative path planning algorithm.

3. Kinematic model of single carrier aircraft or traction system

3.1.A comparison between kinematic model and dynamic model

The dispatch path planning of carrier aircraft is so delicate that the aircraft should be modeled according to the dispatch characteristics,and it is hard to be simply reduced to a mass point.Therefore, it is necessary to establish the corresponding dispatch dynamic or kinematic model that can describe the dispatch motion characteristics of aircraft.

Dispatch dynamic model of aircraft can be accurate to show the behavior and motion characteristics of the dispatch system,the mechanical properties,and external force.Complicated factors,such as the deck surface turbulence and sag,and inertia force, can be accurately described.23,24However, it will lead to a long time of numerical calculations. In addition, the dynamic model involves many parameters, and it is usually necessary to identify the parameters of the dispatch system and adopt multi-body modeling technology to obtain the accurate dynamic model, which also brings inconvenience to the application of dispatch dynamic model for carrier aircraft.

The dispatch kinematic model of aircraft can accurately describe the motion characteristics of the system under the condition of low-speed motion.Compared with the dynamic model,the main advantage of using the kinematic model is that the model structure is simple with fewer parameters to be identified.Additionally, system can also be solved accurately with less computational time.The disadvantage of the kinematic model is that it is based on some premises,for example,(A)the ground is completely flat;(B)the tire does not slide;(C)inertia and lateral forces are ignored.These premises are not applicable for the condition of high-speed motion.However,if the system is operating at a low speed, these assumptions do not significantly affect the accuracy of the results.

According to Karkee’s research on tractor-trailer systems,25the kinematic model can describe the motion characteristics of the system with almost the same accuracy as a dynamic model when the speed of the system is small(approximately less than 4.5 m/s).As the dispatch speed of carrier aircraft on the deck is slow, the kinematics model is widely used to study the path planning of carrier aircraft, and the dynamic model is hardly used in the path planning problem for carrier aircraft.

Based on the assumption made above, the kinematics and corresponding mechanical constraints of three dispatch modes are given in the rest of this section. It is noted that when the aircraft is towed by a tractor, no matter for the tractor with or without a drawbar, the configuration can be categorized into on-axle or off-axle hitching according to whether the hitch between the tractor and the drawbar/carrier aircraft lies on the rear axle of the tractor. Actually, the off-axle hitching is the general form of on-axle hitching. Hence, we will take the offaxle hitching configuration for example when we model the traction system in Section 3.3 and Section 3.4.

3.2. Carrier aircraft autonomous taxiing

When the carrier aircraft taxi on the flight deck by itself, as illustrated in Fig. 3, the positive acceleration and the negative acceleration are provided by the engine and the brake, respectively. And the steering operation is controlled by the nose wheel.

Point （x1，y1）, which is the middle point of the rear axle, is used to represent the position of the carrier aircraft.It is under the condition of pure translation and the corresponding velocity is denoted as vCA. Parameter LCAis the longitudinal distance between the nose wheel and the rear wheel axis. The variable θCAand βCArepresent the orientation of the carrier aircraft and the front wheel steering angle, respectively. When selecting the state space as xa1= ［x1，y1，θCA，vCA，βCA］T, the kinematic equations can be written as

Fig. 3 An illustration of carrier aircraft autonomous taxiing.

3.3. Traction system without drawbar

In this dispatch mode, the tractor provides the power of the whole traction system instead of the carrier aircraft itself,and the steering operation is controlled by the front wheel steering angle of the tractor.An illustration of the traction system without drawbar is shown in Fig. 4. Similar to the modelling process in Section 3.2, Point (x1,y1) and θCAare used to represent the position and the orientation of the carrier aircraft, respectively. The variable θTis the orientation of the tractor.The variable βCAand βTrepresent the nose wheel steering angle of the carrier aircraft and the front wheel steering angle of the tractor, respectively, and we have βCA=θT-θCA. The parameters LTis the longitudinal distance between the nose wheel and the rear wheel axis of the carrier aircraft, while the parameter LTis the wheelbase of the tractor.The parameter M1is the distance between the hitch and the rear wheel axle of the tractor. By velocity decomposition,one can draw the conclusion that the translational velocities of the carrier aircraft and the tractor, which are denoted as vCAand vT, have the following relationship:

Fig. 4 An illustration of traction system without drawbar.

3.4. Traction system with drawbar

The traction system with drawbar can be seen as three-body articulated system, as illustrated in Fig. 5. The variables θ1,θ2, and θ3represent the orientation of the carrier aircraft,the drawbar, and the tractor, respectively. Points (x1,y1) and(x3,y3)are used to represent the position of the carrier aircraft and the tractor. The variables βCAand βTdenote the steering angles of the carrier aircraft and the tractor, where βCA=θT-θCAand βB=θT-θB. The parameters LCA, LB,and LTare the longitudinal distance between the nose wheel and the rear wheel axis of the carrier aircraft, the length of the drawbar, and the wheelbase of the tractor, respectively.And the parameter M2represents the off-axle distance.According to the velocity decomposition,the translation velocity of the carrier velocity and the tractor,which are denoted as vCAand vT, meet the following relationship:

On the basis of kinematic representation of any n-body articulated vehicle proposed by Park et al.,31Johnston et al.developed a kinematic model for the traction system with drawbar by combining the single-body kinematics of each component.32However, this model selects 14 state variables where many of them are abundant for the purpose of imposing constraints in the DIDO software.33It results in huge computational burden in reality. In addition, this model is constructed under the on-axle hitching condition, i.e., M2=0.

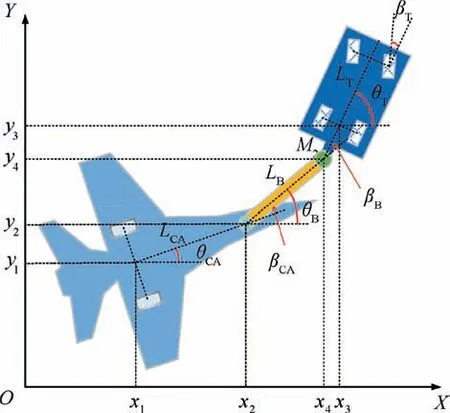
Fig. 5 An illustration of traction system with drawbar.

However, it remains to be verified that whether it can be directly applied to the trajectory planning problem by using optimal control methods due to the extremely high nonlinearity.

4. Path planning techniques for single carrier aircraft

There are typically five kinds of path planning techniques for single carrier aircraft or single traction systems, which are Dijkstra’s algorithm, A* algorithm and its variants, behavior dynamics-based method, intelligent search method, and dynamic optimization method.These techniques can be generally classified into two categories,i.e.,the geometric algorithms and the trajectory planning algorithms, according to whether the kinematic model (or the dynamic model) is considered.The main difference between these two categories is that there is only a series of way-points in the result obtained by geometric algorithms. However, information on time corresponding to the state is also included in the solutions obtained by trajectory planning algorithms. Under this way of classification,Dijkstra’s algorithm, A* algorithm and behavior dynamicsbased method can fall into geometric algorithms, while dynamic optimization method is categorized as a trajectory planning algorithm. And as for an intelligent search method,whether it is a geometric algorithm or a trajectory planning method depends on its formulation.

Various constraints can be considered simultaneously in trajectory planning methods. However, methods in this category could be extremely time-consuming since a complicated optimization problem, which is commonly non-convex due to the highly nonlinearity in system equations and collisionfree conditions, is required to be solved. Compared to trajectory planning methods,geometric methods are much computationally efficient. However, it should be noted that path obtained by this category of methods cannot avoid the possibility of kinematical infeasibility since the kinematical constraints are not accounted. Hence, we cannot simply determine which kind of methods is better. The five kinds of methods and related work are reviewed and their pros and cons are summarized in the rest of this section.

4.1. Dijkstra’s algorithm based method

In this kind of method,the active carrier aircraft is outlined by a circle that contains itself with the radius as minimal as possible,and the circle is called the feature circle of the carrier aircraft.The obstacles in the environment are modelled by convex hulls according to their feature shapes. The threatened zone is obtained by expanding these convex hulls according to the radius of the active carrier aircraft. Then one has to find all way-points within the search zone and compute the cost between each pair of way-points to generate the feasible weighted graph.It should be noted that modelling the obstacle by different feature shapes would lead to distinct manners to define way-points.

Zhang et al.35studied the path planning problem on the flight deck. The dumb carrier aircraft are simply modelled as circles, and the island and a team of dumb carrier aircraft parked in order closely are seen as rectangles. To fulfill the requirement on the terminal heading angle, a predefined way-point is introduced and taken as the new destination.Two tangent circle threatened regions whose radii are the minimum turning radius of the active carrier aircraft are placed at either side of initial position, and their tangent line is in the same direction with initial heading angle. Similar threatened zones are added around the destination. Together with the threatened zones generated by the obstacles, the search space is obtained. It is seen that all candidate path segments consist of arcs and common tangent lines of threatened zones. Then one has to traverse every pair of midpoints of these common tangent lines set corresponding distance cost. Under the same framework, they further study the path planning problem of the traction system.36

Compared with the flight deck, the hangar is a much narrower space with carrier aircraft and other staffs closely stored.Thus,it would be impossible to generate a feasible path for the tracking system if we still model dumb aircraft by their feature circles., Si et al.37studied the path planning problem of the traction system in the hangar,where the dumb aircraft is modelled by the minimum pentagon instead. And all way-points,which consist of the vertexes of threatened zones,are searched by an iterative manner.This method has two drawbacks.First,the final obtained path is composed of several line segments,which suggests that extra smoothening techniques must be incorporated. Secondly, it omits the orientation of the carrier aircraft, limiting its application to scenarios where high demand for terminal orientation exists.

The key in Dijkstra’s algorithm based method is how to generate a feasible weighted graph according to the information on obstacles and the boundary conditions. By using proper strategy to construct the threatened zone, the constraint on terminal orientation and the mechanical constraint on minimum turning radius can be easily taken into consideration. Once the feasible graph is formulated, Dijkstra’s algorithm can efficiently solve the shortest path. However, since the threatened zone and the search space directly depend on the position of obstacles, this kind of method, to the best of our knowledge, has not been applied to environments with dynamic obstacles. In addition, the velocity in this kind of method is constant. Hence, it cannot precisely describe the accelerating motion and the decelerating motion around the initial position and the terminal position, respectively.

4.2. Improved A* algorithm based method

The A* algorithm expands nodes according to the cost function in the following equation:

The constraint on terminal orientation cannot be easily satisfied in the classic A*algorithm.Hence,various improved A*algorithms are developed, where the key is to design a reasonable heuristic function to meet the precision of the terminal orientation and collision-free conditions. And various constraints (e.g., minimum length of path segment, max turning angle,maximum total path length,direction of reaching destination) are integrated simultaneously when expanding path nodes to narrow the search space and correspondingly improve the search efficiency.

To solve the taxiing path planning problem from the elevator to the catapult in obstacle-absent situations, Wu and Qu38proposed an improved A* algorithm with dynamic weighted heuristic function. The heuristic function therein consists of two items, which can be given in the following equation:

By incorporating the idea of Model Predictive Control(MPC) with the A* algorithm, Wu and Xu39designed a new dynamic weight heuristic function and developed a multistep optimization scheme to solve the problem in presence of obstacles.In order to achieve efficient collision avoidance,they extended the heuristic function designed in Ref. 38 to

In both Ref. 38 and Ref. 39, they pointed out that the searching procedure may fail due to the possible condition where constraint on terminal orientation cannot be satisfied in the last step. Hence, as illustrated in Fig. 7, it would be a good idea to start the searching procedure from the destination. However, this trick leads to another issue that the constraint on initial parking orientation cannot be satisfied.Inspired by the skill of introducing an extra way-point around the destination in Ref. 38 and Ref. 39, we think that it would be wise to select a straight-forward point to the initial orientation near the initial parking position and take it as the virtual initial position when applying the A* algorithms.

Fig.6 Multi-step optimization scheme using the idea of MPC.39

4.3. Behavior dynamics-based method

Behavior dynamics-based method is originally developed for path planning problems for mobile robots40,41and recently applied to those of carrier aircraft.It is considered that moving towards the object and obstacle avoidance constitute the path planning behavior modes of carrier aircraft. The velocity and the heading angle are commonly selected as the behavior variables,and the behavior modes are realized by two independent differential equations of these two behavior variables. Actually,this kind of method is,to some extent,similar to the artificial potential field method since the design of fields is the major concern (especially for complicated environment).42When the fields are properly designed, the method shows high efficiency.

Zhang et al.43proposed an improved strategy for obstacle avoidance based on the generalized symbolic threshold function to solve the taxiing planning problem.Recently,the above method is extended to solve the dispatch path of traction systems.44

It should be noted that constraints on terminal orientation are hard to be considered in the behavior dynamics-based method and the design of the field requires high skill.

4.4. Intelligent search method

In this kind of method, the path is first discretized at several points and the state variables or the control variables at discretized nodes are taken as the unknown variables.Then intelligent search methods are adopted to solve the unknown variables and then the complete path is finally obtained. Carrier aircraft are generally modelled by their convex hulls and collision detection algorithm based on convex hulls must be incorporated. A flowchart of general intelligent search algorithm is illustrated in Fig. 8. From Fig. 8, it is seen that there are three key processes when designing an intelligent method,i.e., the encoding formulation of path/trajectory, the evolutionary strategy of population and the selection of fitness function.

Fig. 7 Strategy of starting searching process from the destination in A* algorithms in Ref. 38 and Ref. 39.

Han et al. modelled carrier aircraft by convex hulls and proposed a collision detection algorithm based on convex hulls.45The flight deck is divided into segments along the xaxis direction, and Clustering Particle Swarm Optimization(CPSO) algorithm is used to optimize the corresponding yaxis coordinates. Constraints on minimum segment length,total path length,and maximum steering angle are also considered when formulating the optimization problem.By adopting a multi-population strategy, several spare paths can be generated as well. When the segments of the path are obtained, the extra smoothening procedure is required.This method has two drawbacks: (A) the orientation of the carrier aircraft is not taken into consideration; (B) due to the selected discretization strategy, it inherently lacks the capability to describe the uturn behavior.

In previous work,46Wu et al. took the front wheel angular velocity at Chebyshev collocation points as variables to be optimized, and the Chicken Swarm Optimization (CSO) algorithm was as the core solver.The method in Ref.46 is actually a trajectory planning method since the time variable is considered. A strategy of segmented fitness function is developed,numerical results therein demonstrate that the terminal constraints on position and orientation can be restricted within prescribed ranges. In addition, dynamic and static obstacles can be treated under the uniform framework in this method.However,trajectories obtained by this method are not smooth where many abrupt steering operations exist.

Su et al.47developed a taxiing path planning method that combines artificial experience in selecting intermediate nodes and the Modified Artificial Bee Colony (MABC) algorithm for local optimization.When optimized intermediate path nodes are obtained, the Dubins method or the Reeds-Shepp method is used to generate a feasible trajectory. Hence, the constraints on the minimum turning radius and terminal orientation are strictly satisfied.A similar idea is used in Ref.48,but the genetic algorithm instead is used as the optimization problem solver,where a penalty term and a gene repairing strategy are introduced to accelerate the genetic process. The main drawback of these two methods is that human intervention is necessary since such two algorithms cannot determine the proper amount of intermediate node automatically.

In fact,a proper discretization and unknown variable selection strategy, instead of what intelligent search method is adopted,is the key factor determining the quality of the generated path. Generally speaking, this method owns strong computational robustness and good calculation efficiency.Moreover, it can theoretically achieve global optimality under the given discretization scheme. However, due to the limit of computational time in practice, it cannot avoid the possibility of falling into local optimum.

4.5. Dynamic optimization method

In dynamic optimization method, a nonlinear dynamic optimization problem is formulated by considering various constraints of the system, such as system kinematics, constraints on taxiing velocity, avoidance of input saturation, collisionfree conditions, etc. A general form of constrained optimal control problem is given as

Fig. 8 Flowchart of general intelligent search algorithms.

where J is the cost functional to be optimized and can be set as minimum time, minimum energy, or their linear combination.

It should be noted that,for the purpose of numerical stability, optimal control-based methods usually require that the functions involved are at least C1-continuous(i.e.,the function itself and its first-order derivative are both continuous).Hence,in optimal control-based methods,the active carrier aircraft or traction system is usually seen as a circle,and the obstacles are usually described by the quasi-rectangle, leading to the collision-free condition in the following form49:

Liu et al.29and Shi et al.30studied the path planning problem of the traction system without drawbar using an ODE model and a DAE model,respectively.In both works,the path planning problem is formulated as a minimum energy problem within a fixed domain. The numerical methods adopted in these two studies are both symplectic,leading to sound computational efficiency.

Based on the classic bicycle model, Li et al.50used the Legendre Gauss Pseudospectral(LGP)method to solve taxiing path planning. When formulating the optimal control problem,the terminal time is not specified therein. In Ref. 51,they used genetic algorithms to optimize the catapult allocation scheduling for a team of aircraft launching under a given priority. By relaxing the lower bound of the taxiing velocity to negative, the towing path and time for each carrier aircraft therein are calculated under the framework of Ref. 50.

Johnston and Swenson32focused on the path planning problem of the traction system with drawbar. They took the front-wheel steering angle of the tractor and the velocity of the tractor as control variables and the optimal control was solved by the software package DIDO. However, due to the limit of DIDO, they adopted a kinematic model (it is made up of 14 equations) for the simplicity of imposing constraints.The computational efficiency is extremely low and cannot be applied in real time.

Numerical methods for optimal control problems are divided into direct and indirect methods. Direct methods transform optimal control problems into NonLinear Programming(NLP)which is then solved by NLP solvers.The pseudospectral methods,52as the most popular direct method,have been widely used in solving optimal control problems resulted from path planning of carrier aircraft on the deck.32,50,51In contrast,indirect methods transform optimal control problems into twopoint boundary value problem.Compared with direct methods,indirect methods own higher precision but smaller convergence radius. Wang et al. creatively incorporated indirect methods with pseudospectral discretization and constructed a series of Symplectic Pseudospectral Methods (SPMs).53-55The SPMs were then applied to path planning of various autonomous systems, including carrier aircraft on the deck. Compared with direct pseudospectral methods, constraints are satisfied more strictly and the computational efficiency is higher,which makes SPM an appealing method for solving path planning of carrier aircraft on the deck.

Though optimal control based methods own incomparable advantages over other kinds of path planning techniques, two shortcomings limit their wide application in reality.On the one hand, it is well-known that the solution of a nonlinear optimization problem severely depends on the quality of initial guesses. Hence, for the complicated flight deck environment,the solving procedure could be extremely time-consuming or even failed without proper initial guesses on state and control variables. And such effect of initial guesses is more significant for indirect methods. On the other hand, once carrier aircraft are closely parked, e.g., in the hangar, it is impossible to generate a path because the feature circle wastes too much feasible space.

At the end of this section, a brief comparison of the above five kinds of dispatch path planning method is provided in Table 2.

Table 2 Performance comparison among five kinds of dispatch trajectory planning methods.

5. Coordinated path planning techniques for multiple carrier aircraft

In the previous section, we reviewed the existing research on path planning techniques for single carrier aircraft. However,for launch mission in reality, there are usually more than one carrier aircraft to be dispatched.On the one hand,if decisions are made manually,the complicated situation is hard for staff. On the other hand, if we still adopt the path planning technique for single carrier aircraft, only one carrier aircraft is allowed to taxi on the flight deck. If so, much sparse space on the flight deck will be underutilized, leading to extremely low dispatch efficiency.51Hence, coordinated path planning techniques for multiple carrier aircraft are of more practical value than those for single carrier aircraft.

According to the core mission, research related to coordinated path planning for multiple carrier aircraft can be put into two categories. In the first category,56they only focus on how to generate a feasible path from the initial parking position to the destination for multiple carrier aircraft taxiing on the flight deck simultaneously. In the second category,57-59they focus on modelling and optimizing the sortie task scheduling,where the path planning for multiple carrier aircraft is seen as an independent module that integrates to the upper-level mission planner. The path planning module generates crucial information (i.e., the taxiing distance and the taxiing time)for evaluating a certain sortie scheduling and outputs it to the top-level optimization solver.

Liu et al.56proposed a compound path planning technique for multiple carrier aircraft. The Reciprocal Velocity Obstacle(RVO) method60is an efficient obstacle avoidance and path planning method for a multi-agent system. Based on the concepts of the RVO method and the Dubins curve method, an improved Dubins-RVO method is constructed. In the Dubins-RVO method, various kinds of constraints (i.e., the kinematic model, maximum front wheel turning radius, and maximum taxiing velocity) are considered. Thus, compared to the classic RVO method, the improved Dubins-RVO method can effectively avoid the ‘‘dead-lock” phenomenon.However,RVO-like methods have several inherent drawbacks.On the one hand,when an agent approaches the destination,it wanders around the destination rather than comes to a complete stop. On the other hand, the orientations of agents are not considered. To overcome these two shortcomings, as shown in Fig.9(a),the whole taxiing trajectory of each carrier aircraft was decomposed into two stages.In the first stage,aircraft taxies from the initial parking position to a position near the destination,i.e.,approximately the distance of two times of the minimum turning radius away. And in the second stage,the aircraft completes the remaining path. In the first stage,the improved Dubins-RVO method as illustrated in Fig. 9(b)is applied to realize efficient obstacle avoidance.As for the second stage, it is assumed to be an obstacle-free condition (and the assumption is reasonable according to the real flight deck environment), and the One-Sided Symplectic Pseudospectral(OSSP)method is adopted to generate the remaining path that strictly satisfies the prescribed terminal orientation.

Fig. 9 Main idea of compound path planning method in Ref.56.

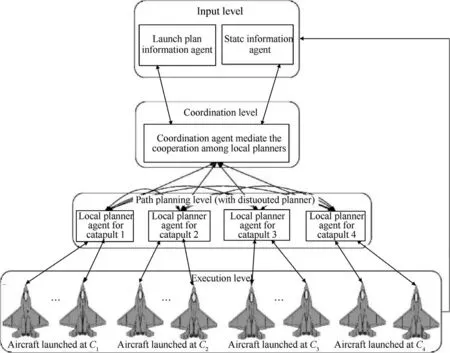
Fig. 10 Hierarchical distributed mission planning architecture in Ref. 58.

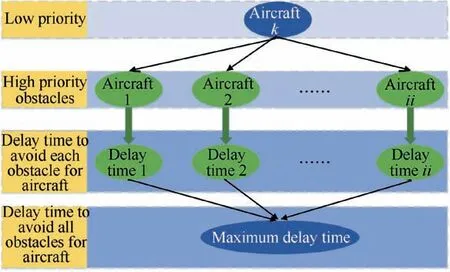
Fig. 11 Strategy to determine the waiting time adopted in Ref.59.

Li et al.57studied the path planning for aircraft fleet launching on the flight deck of carriers with limited space and resources, according to the launching plan received. An improved A* algorithm with a segmented dynamic weighted heuristic function is adopted. A top-level mathematical model that determines the total consumption of aircraft fleet launching is established at first. This model contains the constraints of maneuverability, the work mode of catapults, ground motion,and collision detection of aircraft taxiing on the flight deck.As stated previously,since the path obtained by A*algorithms consists of several path segments, extra smoothening techniques must be incorporated to get the feasible path.Thus,it will be a two-step process to get the feasible path,and cannot guarantee that the path meets the constraints of maneuverability. Therefore, the path tracking is combined with path planning method developed in Ref. 39. When generating the taxi path for a period of time in future, the rolling optimization method is used to optimize the formulated performance index of path tracking, and the planning domain and the control domain are defined to execute the optimal control instructions(the nose wheel steering angle is selected therein) only over a short period of time. Not only the constraints of a single aircraft are considered, but also collision detection is executed multiple times in each step of the path search to ensure the safety of each path. It should be noted that the aircraft must track the planned path in a chronological order.

Focusing on the same issue with Ref. 57, Wu et al.58proposed a novel distributed mission planning architecture. The architecture is hierarchical and is comprised of four levels as illustrated in Fig.10,namely,the input level,the coordination level,the path planning level,and the execution level.Realistic constraints in each level of the distributed architecture,such as the vortex flow effect, the crowd effect, and the motion of aircraft are considered in this model.A distributed path planning algorithm is developed, and an asynchronous planning strategy based on token passing that can avoid the dead lock and Buckets effect is adopted.

Liu et al.59described the sortie scheduling as a Flexible Flowshop Scheduling Problem (FFSP) model, and the collaborative trajectories planning of taxiing for multiple aircraft is the core stage therein. In Ref. 59, the pre-determined timing scheme of the sortie task is used as the input of collaborative trajectories planning of the taxiing of multiple aircraft, and optimal scheme is finally obtained by the dynamical adjustment of the pre-determined timing scheme according to collaborative trajectories planning. To solve the collaborative trajectories planning,the OSSP method is adopted to calculate the offline feasible trajectories from each gate position to all catapults/preparation spots,and the obtained paths are stored in the trajectory database. Then the timing sequence of each aircraft is optimized according to the priority principle. This method is robust since it inherently avoids the ‘‘dead-lock”phenomenon. However, as illustrated in Fig. 11, the collision avoidance strategy in this method is not rich, where aircraft with lower priority can only wait for the aircraft with higher priority until the collision does not happen.

6. Trajectory tracking

As discussed in Section 4 and Section 5,control inputs cannot be obtained simultaneously with the path except for optimal control based methods. Actually, even for optimal controlbased methods, the obtained control input still cannot be directly applied to the carrier aircraft or the traction system due to the existence of various disturbance.There are generally two kinds of disturbances considered in the existing research,including the disturbance in the initial parking position and the continuous external disturbance induced by the wind and sway of the aircraft carrier.

Hence, it is necessary to adopt a closed-loop controller,where the MPC control is frequently used, to track the reference trajectory provided by the motion planner.In this section,the basic mathematical formulation of the MPC trajectory tracking controller is given first. Then, related researches on the trajectory tracking of carrier aircraft are reviewed. Skills to design a better MPC controller are then discussed. Finally,the analogy of trajectory tracking between carrier aircraft and other vehicles is provided.

6.1. Mathematical formulation of MPC trajectory tracking controller

The MPC controller is designed based on the idea of receding horizon optimization. There are typically two forms of MPC,i.e., the continuous and the discrete form. In this section, the continuous form is considered due to its wider application in the trajectory tracking problem of the carrier aircraft.

Fig. 12 An illustration of model predictive controller.

where the variable e is used to represent the error between the actual trajectory and the reference trajectory; the matrices P and R are weighted matrices on tracking error and control inputs, respectively; h represents the constraints considered,which may contain constraints on control variables,collision-free conditions, maximum allowable taxiing velocity,and other necessary mechanical constraints.

An illustration of the MPC controller is given in Fig.12.It is seen that when the open-loop optimal control problem is solved,the first step following in the control sequence is taken as the control input for the current control window. And taking the autonomous taxiing as an example, an overall procedure of the MPC trajectory tracking controller is provided in Fig.13.

6.2. Related work

Zhang et al.35-36studied the path planning problem for carrier aircraft and traction systems without drawbar, respectively.When the feasible trajectory is obtained, the MPC controller is applied to track the reference trajectory. Numerical results therein demonstrate that the terminal errors, including both position error and orientation error, are within an allowable range. However, the purpose of applying the MPC tracking controller is only to verify the feasibility of the reference trajectory and no perturbation is considered therein. Besides, the control variable (e.g., the steering angle of the tractor in Ref.36) may vary sharply since the actual control saturation is not considered.

Liu et al.29focused on the path planning and tracking control of the traction system without drawbar.Similar to the offline path planning module, the kinematic model given in Eq.(15) is used for the online path tracking module. Numerical results therein suggest that the initial error can be quickly eliminated by the MPC controller, and the MPC controller can efficiently track the reference trajectory even under continuous external disturbances. By using the symplectic pseudospectral MPC controller developed therein, the average computational time for each sampling instant can be restrained within 10 ms,satisfying the real-time calculation demand.

Fig. 13 An overall procedure of MPC tracking controller for carrier aircraft autonomous taxiing.

Liu et al.56studied the cooperative taxiing path planning of multiple carrier aircraft. When the feasible trajectory of each carrier aircraft is obtained, the MPC controller is applied to track the reference trajectory separately. However, as for the kinematic equations used when designing the MPC controller,they further removed the taxiing velocity from the state variable form the model in Eq.(6)and meanwhile took the taxiing velocity and the front wheel steering angle as the control inputs. Numerical results therein show that taxiing velocity jumps between the maximum allowable value and zero fast,which means that the carrier aircraft frequently comes to a full stop during the taxiing.On the one hand,it is not possible for the engine to switch that fast.On the other hand,even though the fast on-off switch of the engine is allowable, the frequent acceleration-deceleration could make the pilot extremely uncomfortable.

6.3. Some skills in designing the MPC controller

6.3.1. Selection of kinematic model

It is seen that the kinematic model used in the MPC controller is identical to or much simpler than that used in trajectory planning in most studies. However, this may cause that some variables vary extremely fast within the designed allowable range.Hence, it is necessary to use a relatively precise model in the MPC controller.For example,one can use the kinematic model(6)in trajectory planning while using the kinematic model(1)in trajectory tracking. Thus, by taking the front wheel steering angular velocity instead of the front wheel steering angle as a control variable, the profile of the front wheel steering angle obtained by the MPC tracking controller would be smooth.

6.3.2. Setting of allowable ranges of state and control variables

Considering the existence of external disturbances,the bounds set in the tracking module should be slightly larger than those in the planning module. Otherwise, the tracking error cannot be effectively restrained or even diverge in the presence of large external disturbance. A reasonable strategy is that: (A) first,when conducting path planning,the necessary bounds imposed should be much tighter than corresponding allowable ones;(B)then, when conducting trajectory tracking, the bounds imposed can use the maximum allowable ones.

6.3.3. Setting of collision-free conditions

In fact, safety distance is usually prescribed in the trajectory planning module. Hence, when sufficient safety distance is given,it is unnecessary to consider the collision-free conditions when designing the MPC controller if external perturbations are not large. Eliminating the collision-free conditions in the MPC controller could extremely improve the online computational efficiency.29

However, for the sake of safety, one may introduce a constraint that restrains the deviation between the actual and the reference trajectories within a relatively small range.56Such a constraint can be expressed as

6.3.4. Design of cost function

When designing the MPC controller, one can simply set the control related term as uTu,i.e.,the weighted matrix on control input R is set to be an identity matrix. Thus, the design of tracking error-related terms could severely influence the tracking performance.Since we mainly focus on the tracking performance of carrier aircraft itself, the elements in the matrix P corresponding to the state of carrier aircraft should be assigned with bigger values.

6.3.5. Design of initial guesses

For the MPC controller, an open-loop optimal control problem is required to be solved at each sampling instant, and the quality of initial guesses may severely determine the computational efficiency. If the actual trajectory does not deviate much from the reference trajectory, one can directly take the interpolation of reference trajectory as initial guesses.An alternative way is that, the solutions obtained at the current sampling instant are interpolated and then form the initial guesses for the next sampling instant.

6.3.6. Selection of the length of prediction window

The appropriate length of the prediction window is of great significance to ensure the tracking accuracy and efficiency. If the window is too short, it is difficult for the system to eliminate large errors in a very short period of time under the control-constrained condition, which may lead to divergence.If it is too long, the calculation accuracy and calculation efficiency in a single window are usually difficult to be taken into account.

6.4. Analogy of trajectory tracking between carrier aircraft and other vehicles

Research on the dispatch trajectory tracking of carrier aircraft is rarely seen. However, a lot of research results have been obtained in the field of UAVs and UGSs. The widely used tracking control methods can be divided into geometric and kinematic tracking control methods,61classical tracking control methods,62methods based on dynamic state feedback,63,64instantaneous optimal control,65methods based on neural network,66,67fuzzy logic,68,69etc.

The general idea of trajectory tracking for dispatch on deck is similar to tracking problems for other vehicles.However,the motion of carrier aircraft is much susceptible to various kinds of external disturbances whose magnitudes may vary according to the position of aircraft on the deck. Since the security is the‘‘lifeline”to carrier aircraft,it puts a higher requirement on the control performance of the tracking method used.

Tractor-aircraft systems can be seen as tractor-trailer systems. However, most studies on the tractor-trailer system merely focus on the tracking of tractor, and most tracking algorithms can only solve the problem of reversing or forward driving of the system. It is mainly because the kinematics or dynamics of the system is relatively complex, and the tracking process of switching between reversing and forward driving is easy to diverge.The existing methods are difficult to effectively solve the trajectory tracking control problem of this process.Therefore, how to make a method robust is a key research direction in this field.

7. Outlook

Considering the limits and constraints of the existing trajectory planning methods of carrier aircraft,future research directions are discussed in this section.They are concerned with the compound of different algorithms,path planning of heterogeneous dispatch systems, the selection between distributed and centralized path planning methods, and integration with machine learning techniques.

7.1. Compound of different algorithms

As discussed in Section 4,each path planning algorithm has its advantages and disadvantages. An appealing idea is to utilize two or more of them to construct a compound path planning method where the advantages of them can be explored. There are typically two manners to combine two isolated path planning algorithms.

In the first manner,the whole path is divided into two parts by the prescribed criterion. And two different path planning algorithms are applied to two parts of the path respectively.The algorithm should show its unique advantages in solving the path planning problem with characteristics in which part it is applied. Liu et al.56just adopted this manner to combine the improved Dubins-RVO and the idea of optimal control to develop a compound taxiing path planning method for multiple carrier aircraft.

In the second manner, the results obtained by one algorithm are taken as the initialization of another algorithm.This manner is not used in the path planning of carrier aircraft yet,but has been widely used in path planning of AGVs.For example, to solve the path planning of AGV efficiently, Li et al.26proposed a first-search-then-optimize approach. In Ref. 27, a rough path is first generated by the A* algorithm and then taken as the initial guesses in optimal control based method,thus accelerating the solving procedure of the optimal control problem.

By introducing a proper compound strategy, it is possible to construct a fast planning method which could provide paths of high quality.

7.2. Path planning of heterogeneous systems on the deck

The heterogeneous properties can fall into two categories. On the one hand, there generally would be vehicles of heterogeneous configurations running on the flight deck simultaneously. A common scenario is that during a sortie task, some of the carrier aircraft taxi autonomously while others are towed by tractors. A more special scenario is that when an autonomous taxiing carrier aircraft breaks down, an extra tractor is required to quickly tow it away to make clear space for following dispatch. In the above two scenarios, dispatch systems of more than one single configuration are involved.It leads to the coordinated trajectory planning problem of heterogeneous configurations.70,71Actually, the coordinated path planning methods mentioned in Section 5 are still capable of dealing with the heterogeneity in configurations. However,to the best knowledge of authors, related research is rarely seen. On the other hand, the functions of aircraft in a fleet launching process are generally heterogeneous, and aircraft of different types should collaborate to execute a task.72Hence,there might be precedence constraints on the launching order for aircraft in the fleet.Coordinated path planning techniques that consider precedence constraints,such as in Ref.59 and Ref. 72, can effectively deal with the issue.

7.3. Selection between distributed and centralized path planning methods

The cooperative path planning methods can be generally divided into distributed planning methods and centralized planning methods.73,74

In centralized planning methods,the state of all individuals must be considered simultaneously. It does not need much communication between different individuals.75,76However,it leads to a large-scale planning problem and the corresponding solving procedure would be extremely time-consuming.77And the path tracking cannot be implemented until the whole solving procedure ends. If extra obstacles appear suddenly in the environment, the previous obtained feasible path fails,and the carrier aircraft should slow down and wait for the result for a new plan.

Different from centralized cooperative path planning methods, paths of each carrier aircraft are gradually generated in a chronological order in distributed methods.78,79Thus, when a small part of the feasible path is generated, the path tracking can be carried out immediately. This leads to the ‘‘simultaneous path planning and tracking”.58Another advantage of distributed methods over centralized methods is that the planning can go on when other obstacles suddenly appear.However,the distributed path planning methods require all individual to communicate with each other frequently, resulting in a high communication burden in practice.

Since the on-board computing devices nowadays generally cannot meet the requirement of the real-time computational efficiency for centralized planning methods, distributed cooperative path planning methods of multiple carrier aircraft draw much attention than centralized ones.However,the authors do believe that more researchers, in the future, will focus on centralized planning methods when high-performance computing devices are equipped on the aircraft carriers.

7.4. Integration with machine learning techniques

Machine learning techniques have been successfully applied to path planning problems in other fields, such as asteroid landing,80space debris removal,81interplanetary trajectory planning,82mobile robot,83etc. However, machine learning techniques have not been applied to the path planning of carrier aircraft.

Sample-based methods, such as SVM,84deep learning,85etc., rely on high-quality and large-scale samples. It is necessary to design the appropriate input and output indicators for the path planning problem. Actually, the dispatch path of carrier aircraft and the corresponding operational commands of the pilot are precious data and can be utilized to construct sample-based machine learning based path planning techniques. However, the record of such data has not drawn much attention.

Reinforcement learning, as the most popular machine learning techniques since the last decade,has been widely studied in path planning.86It can directly interact with the environment without establishing an environment model, having any prior knowledge, or training with expected samples. Hence,many researchers have applied it in the field of path planning and achieved a lot of results.87However, the training process in reinforcement learning could be extremely time-consuming.

One of the most concerning issues in machine learning techniques is the generalization capability.Unlike the environment for self-driving urban vehicles, the operational environment for dispatch on deck is relatively fixed.17Thus, a reliable path or control commands can be generated quickly once the neural network is well trained. One thing to be noted is that various constraints may not be strictly satisfied in the results obtained by machine learning techniques. Hence, it seems appealing to take the obtained results to initialize other path planning methods, as discussed in Section 7.1.

8. Conclusions

The path planning of carrier aircraft on the deck is a key technology for the sortie and recovery task. Based on the present research and development of carrier aircraft’s dispatch path planning technology and the related works,this paper reviews the latest developments and current status of carrier aircraft’s dispatch path planning on the deck.Furthermore,the analogy of path planning between aircraft dispatch and other fields such as UGSs is discussed. Finally, the future research directions are discussed. By synthetically adopting the path planning and control techniques, it is promising to realize the autonomous dispatch for carrier aircraft on deck in the future.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors are grateful for the financial support of the National Key Research and Development Plan (No.2017YFB1301103), the National Natural Science Foundation of China (Nos. 11922203, 11772074, 11761131005), and the Fundamental Research Funds for the Central Universities(Nos. DUT19TD17, DUT19TB18).