改进遗传算子的测试用例优化研究

刘 音

（北京交通大学海滨学院 河北·沧州 061199）

0 引言

软件测试的主要目的是通过执行测试用例检测出所有隐藏的错误，是软件质量保证的重要手段。测试用例（Test Case）是由一组测试输入、执行条件及预期结果组成的，是用于衡量软件是否存在错误的主要依据，它的数量和质量直接决定了测试效率和成本。随着软件规模不断扩大，测试用例集规模也会越来越大，其中的冗余测试用例也会随之增多，测试成本也就随着增大。为了有效降低测试成本，有必要对测试用例集进行优化，即在保证原检测错误能力的基础上，寻找原始用例集的一个子集，使其覆盖所有测试需求，且保证运行成本最小。

遗传算法（Genetic Algorithm,GA）是将生物进化过程中适者生存规则与种群内部染色体的信息随机交换机制相结合的高效全局寻优搜索算法。作为一种全局搜索方法广泛应用在测试用例优化领域中，有着独特的优势和高效性。

1 改进遗传算子

遗传算法是由进化论和遗传学演化而来的一种直接搜索优化方法。它将所有可能解看成是种群的一个个体，依据适者生存、优胜劣汰的进化原则，进行选择、交叉和变异操作，最终得出问题最优解。但遗传算法中存在以下问题：

（1）早熟现象，即过早陷入局部最优解，而很难走向全局最优。

（2）在选择操作过程中，适应度高的个体作为父代，可能导致遗传基因趋于一致，也就是存在很多相似的个体，减少了种群的多样性。

鉴于以上问题，本文对选择算子、交叉算子和变异算子进行了改进，进而形成了一种新的改进的遗传算法（Improved Genetic Algorithm,IGA），并用改进的遗传算法实现测试用例集缩减。

1.1 改进选择算子

选择算子作用就是依据个体适应度值，从父代种群中选择若干个体遗传到下一代。轮盘赌法通过随机性，保证了下一代种群的多样性，但同时会使降低高适应度个体选中概率难以收到最优解。改进的选择算子是将排序与轮盘赌相结合的方法，增加了优良个体的选择概率，具体操作过程如下：

（1）种群中的个体按其适应度的高低降序排列。

（2）对排好序的个体按5%、90%和5%分成三份，并用前5%的个体代替后5%的个体。

（3）计算个体适应度 F(Ti)，i=(1,2,……，M)，M 为种群规模。

（4）计算选择概率：个体适应度值除以总适应度值，如公式（1）所示。其中，P(Ti)为个体选择概率，F(Ti)为个体适应度。

（5）计算个体累积概率，如公式（2）所示，其中Qi表示个体累积概率。

（6）产生一个随机数r，r在[0,1]范围内。

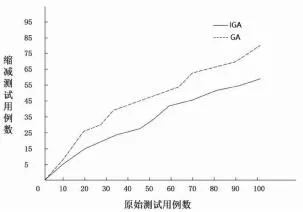
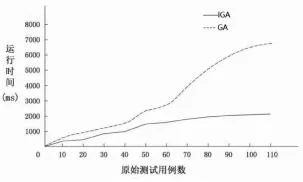
（7）若r

（8）重复7、8步骤M次。

1.2 改进交叉算子

交叉操作就是两个配对的个体按照某种方式交换某位基因或者某些位基因，从而产生新个体的过程。交叉类型有：单点交叉、两点交叉、多点交叉和均匀交叉等，本文采用单点交叉，实现过程是在交叉点的位置相互交换两个配对个体的部分染色体。

交叉概率用于判断两个个体是否需要交叉，在遗传进化过程中，为保留优良个体应尽量降低其交叉概率，为优化劣质个体应尽量增加其交叉概率。本文提出了新的计算动态交叉概率方法，如公式（3）所示。

其中，f'表示两个预交叉个体的高适应度值，fmax为所有个体中的最大适应度值，fmin为所有个体中的最小适应度值，M1是适应度值大于等于平均适应度值的个体总数，M2是适应度值小于平均适应度值的个体总数，favg是平均适应度值，Pc1和Pc2是两个初始交叉概率、分别设置为：Pc1=0.5，Pc2=0.9。这样就能保证进化初期，有较大的交叉概率，保证种群多样性，并且适应度小的个体交叉概率更大；而在进化后期，交叉概率相对较小，加快算法收敛。

图1：用例集缩减规模

1.3 改进变异算子

变异操作是模仿个体进化过程中染色体的某个基因值发生突变过程，例如：采用二进制编码方式的个体，变异操作就是1变0或0变1。在变异操作中起关键作用的是变异概率，如果变异率较小，容易出现早熟现象，如果过大，会出现随机搜索现象。本文提出了新的变异概率计算方法，如公式4所示。

Pm1和Pm2是初始变异率，Pm1=0.001，Pm2=0.005，fmax和fmin与公式8相同，f表示个体适应度。适应度小的个体变异率大，可以改良基因；适应度大的个体变异率小，优良基因可以遗传给下一代。

2 IGA实现测试用例优化

利用改进遗传算子解决测试用例优化问题时，首先根据测试用例与测试需求之间的覆盖关系，形成初始个体集合，然后通过选择、交叉和变异操作，求出测试用例集缩减问题的最优解。

2.1 测试用例优化

测试用例优化又称为测试用例约简，是M.J.Harrold等人在1993年提出的。早期，在测试用例缩减过程中并没有考虑测试用例的运行代价，导致执行缩减后测试用例集代价并不能降低到最小。缩减过程中不仅要考虑测试需求覆盖度，还要考虑测试用例执行代价，测试用例集约简的定义：给出一组测试需求集R={r1,r2,r3,…,rm}，一组与测试需求相关的测试用例集T={t1,t2,t3,…,tn}，每个测试用例ti都有相应的测试代价ci（ci>0），测试用例缩减问题就是求T的一个真子集T’，满足：T’的运行代价最小，并且T’能覆盖R。测试用例缩减结果就是满足表1中的每行至少被一列覆盖，且使“1”个数最少。

2.2 基因编码

基因编码就是把问题空间的数据转化成遗传空间的由基因组成的个体，常用编码方法有：二进制编码、浮点编码和符号编码。二进制编码就是由符号0和1所组成的二值符号集，编码、解码操作简单易行，交叉、变异等遗传操作便于实现，故本文采用这种方法进行基因编码。根据测试需求和测试用例对应关系构建一个m×n矩阵：

图2：算法运行时间

R表示测试需求集，T表示测试用例集，m表示矩阵的行数、由测试需求的个数决定，n表示矩阵的列数、由测试用例个数决定。gij表示用例tj和需求ri之间的覆盖关系，如果gij=1表示tj覆盖ri，反之gij=0表示tj没有覆盖ri。矩阵中的每一行表示了一个需求被所有用例的覆盖情况，把每一行看成一个个体，采用二进制基因编码如公式（6）所示。

2.3 适应度函数

适应度是用来判断种群中个体优劣程度的指标，并作为遗传操作的依据。一般地，适应度值越大，表明相应的个体越优，它的基因被复制到下一代的概率就越大，个体适应度函数表示如公式（7）所示。

Cov(Tj)是用例集Tj的测试覆盖度，计算方法如公式（8）所示。

Cost(Tj)是用例集Tj的运行代价，计算方法如公式（9）所示，用测试时间执行时间粗略表示其运行代价。Cost(ti)表示执行ti测试其覆盖需求所用时间。

当个体的适应度达到给定的阈值或者个体的适应度不在上升或者迭代次数达到阈值，终止计算。本文采用迭代次数达到阈值作为终止条件，最大迭代次数为150。不满足收敛条件时，重复遗传操作，直到收敛到最优解。最后，根据测试用例与需求的覆盖关系进行解码，获得缩减后的测试用例集。

3 实验结果与分析

为验证改进遗传算法性能，在MATLAB仿真实验的环境下，完成了测试用例优化系统的设计与实现。以BBS论坛模拟程序为测试对象，从缩减测试用例规模和测试用例执行时间这两方面对遗传算法和改进遗传算法进行对比。

首先，从缩减测试用例规模上对比GA和IGA，实验结果如图1所示。每条曲线表示原始测试用例数量与缩减后测试用例数量之间的对应关系。从结果可以看出，IGA缩减测试用例后规模明显小于GA，且缩减规模更稳定。然后，对比GA和IGA缩减后的测试用例集运行代价（时间），实验结果如图2所示。从结果可以看出，IGA缩减后的运行时间比GA的运行时间更低。

4 结束语

针对遗传算法容易陷入局部最优解问题，本文从选择算子、交叉算子和变异算子三方面进行改进，得到了一种改进遗传算法，并将其应用在解决测试用例集缩减问题。通过仿真实验得出：

（1）改进遗传算法的收敛性优于遗传算法，可以更好的缩减测试用例规模。

（2）改进遗传算法缩减测试用例能更好的降低运行代价。

（3）应用改进遗传算法缩减测试用例后得到的用例集与原测试用例集相同的错误检测能力。

改进遗传算法可以有效降低测试用例冗余度，减小了测试用例规模，缩短了测试时间，并且保证了缩减后的测试用例有着原测试用例集的检错能力。但也存在问题，如：采用单点交叉，随机基因重组不能保证大概率地生成优于父代的个体。在未来工作中，笔者将继续致力于测试用例集约简的研究。