浅谈《大学物理》中的高斯定理在静电平衡中的应用

刘世杰 杜 慧 王晓飞 郝世明 李同伟

（河南科技大学物理工程学院 河南·洛阳 471023）

根据物质的导电性能对其进行分类，可以分为三个类别，分别是导体、半导体和绝缘体。对于本文中，我们主要讨论导体的静电平衡性质，这是由于导体中存在大量自由电荷，当外电场改变时，电荷可以进行自由移动，进而达到导电的效果。具体而言，当把导体放置于一个外电场中，相较于无电场状态，导体中大量存在的自由电荷就会在外电场的作用下做定向移动，进而在导体表面出现电荷的重新排布，进而使导体的一边聚集正电荷而带正点，另外一侧聚集负电荷而呈现出负点，这一现象即为静电感应。在导体两侧由于外电场而出现的电荷，我们习惯上称作感应电荷。假设外电场恒定，则由于外电场的持续作用，导体内部正电荷持续由原来位置移动到与电场方向相同的导体表面一侧，而负电荷（电子）会持续地移动到与外电场方向相反的导体表面一侧，也即是导体表面上的感应电荷逐渐增多。感应电荷同样会产生电场，习惯上叫做附加电场，如图1（左）所示。从图中我们可以很清楚地看到，附加电场的方向与外电场方向相反，则导体内部的合电场应为附加电场和外电场的矢量和。随着时间的持续作用，电荷持续在导体两侧堆积，附加电场逐渐增大，当附加电场增加到与外电场大小相等，方向相反时，导体电荷达到平衡，这一现象我们称之为静电平衡，如图1（右）所示。

图1：导体的静电平衡过程

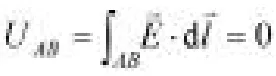
在实际中，静电平衡时导体中电荷分布情况往往十分复杂，而利用高斯定理则可以直观的分析导体的电荷分布情况。

1 实心导体的电荷分布

首先分析最简单的情况，也即是实心导体的情况。如图所示，当体系达到静电平衡时，由于附加电场的作用，导体内部的电场强度处处为零，也即是。此时，如果我们在导体内部选取一个如图2所示的高斯面S，则，由高斯定理我们可以得到：高斯面内电荷量的总和也为零。因此，当我们可以得到导体内部处处无电荷存在，并且只能存在于导体表面。

图2：实心导体的电荷分布

2 当导体中存在空腔时的电荷分布情况

2.1 当导体空腔内不存在电荷时

当空腔内无电荷的导体在静电场中达到静电平衡时，由静电平衡时附加电场与外电场抵消，也即是导体内部。同样地，在导体内部任意选取一高斯面 S，同样满足，任意选取的高斯面S内的净电荷必定等于0，即电荷只能在导体表面存在。假设空腔内表面存在感应电荷的话，我们可以选取一个任意的高斯面S，该高斯面如果恰好把全部空腔的内表面都包围，则该高斯面必然满足，即感应电荷必然等量异号，如图3所示。

图3：空腔内无电荷时导体的电荷分布

通过上面分析，可以得到结论：当导体为空腔导体且其中没有电荷存在时，电荷仅仅分布在导体的外表面上，导体的内表面则没有电荷存在。

2.2 空腔导体的内部存在电荷量为q时

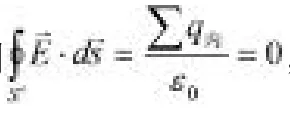
图4：空腔内无有电荷时导体的电荷分布

由此得出结论：空腔内有电荷q时，空腔内表面必然存在由于静电感应而产生的电荷q，外表面也会存在电荷量为q的感应电荷。

3 真空中孤立存在导体表面的电荷分布

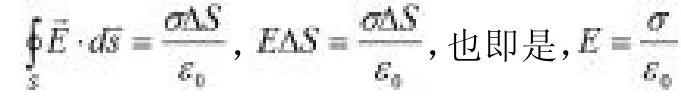
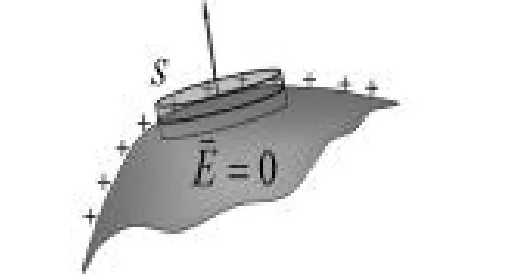
图5：孤立导体表面电场强度

对于孤立导体而言，其表面上的电荷面密度反比于其表面的曲率半径。如图6所示，存在一个处于静电平衡态的孤立带电导体，假设左侧比右侧尖锐，也既是左侧曲率半径更小，则左侧表面的电荷面密度较右侧更大，左侧表面的电场强度也较右侧更大。当然，影响导体表面电荷分布的因素除了导体的形状之外，还存在其他的因素，比如外部环境等。在一些特殊情况下，一些形状较为尖锐的带电孤立导体就有可能产生尖端放电现象。由于导体尖端电荷面密度很大，使导体尖端表面的电场强度极高，此时就有可能将其周围空气电离而形成通路产生电火花等放电现象。

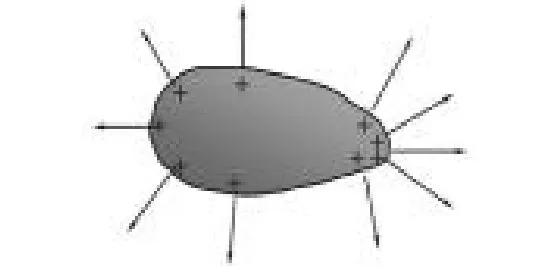
图6：孤立导体表面电荷分布