基于改进范数约束LMS 算法的数字预失真技术

王 鑫，李思敏，叶金才，王国富⋆

（1.广西科技大学，广西 柳州 545000；2.桂林电子科技大学，广西 桂林 541000）

0 引言

近年来许多学者对数字预失真系统提出很多有效的模型，并通过实际工程验证其取得了不错的效果。但是，人们在预失真器的行为模型辨识方面的研究较少，识别算法的性能影响整个预失真系统的非线性补偿效果。传统自适应最小均方（Least Mean Square，LMS）算法、归一化最小均方（Normalized Least Mean Square，NLMS）算法以及递归最小二乘（Recursive Least Squares，RLS）算法，在系统识别、工程控制等领域应用广泛。然而，在实际的大容量数据和低信噪比环境下，传统最小均方算法无法对未知行为模型进行有效识别。Gu Y 等结合LMS 算法与范数特征［1］，设计出有一定范数约束的LMS 算法；Su G 等对算法进行了必要的性能分析［2］；基于分析基础上，Chen Y 等提出再加权零吸引项最小均方（Reweighted Zero-Attracting Least Mean Square，RZALMS）算法［3］，但该算法不能根据自身性能选择合适的零吸因子。文献［4］在文献［5］的基础上，提出改进变换步长的归一化最小均方（Improved Variable Step-Size Normalized Least Mean Square，IVSNLMS）算法，对于信号出现稀疏状态的情况能够实现快速收敛。文献［6］提出了一种通过增加误差信号的相关性来提升系统抗噪性能的算法。文献［7］提出了一种自适应随机梯度变步长最小均方（Adaptive Variable Step Size Least Mean Square，ALMS）算法，通过改变步长因子，并根据EWMA 更新权向量，加快了收敛速度，但无法在低信噪比与混合噪声中正常收敛。本文首先介绍数字预失真模型，根据模型特点介绍算法改进的具体细则。仿真结果证明，基于该算法的数字预失真效果与传统算法相比有较大改善。

1 数字预失真模型介绍

在数字预失真（Digital Pre-Distortion，DPD）系统中，主要通过预失真器构造一个与功放行为相反的逆模型，使系统在保证放大效率的同时降低非线性失真对信号的影响，实现对输入信号的线性放大［8］。

数字预失真主要分为直接学习结构与间接学习结构。间接学习结构通过识别功放的后逆模型代替其前逆模型，降低了功放非线性失真影响，达到了线性输出效果［9-11］。但间接学习结构中，后逆模型与前逆模型存在偏差，使得后逆模型并不是最理想的解。但是，在一些特大型发射系统中，这种偏差可忽略不计。直接学习结构识别功放的前逆模型，直接对功放输入与反馈输出建立逆模型。它的模型识别建立在不断迭代的基础上，在达到稳态后，预失真系统输出信号与输入信号相同［12-15］。然而，它的收敛识别过程中迭代次数明显高于间接学习结构，且在收敛状态下稳态误差较大，易受到噪声干扰而产生波动［11］。

因此，基于传统最小均方算法，针对直接学习结构收敛速度慢、抗噪性能差以及稳态误差偏大等问题，引入基于二范数约束最小均方算法（Two Norm Constraint Least Mean Square，2-LMS）算法作为预失真器模型识别算法，以优化整个系统的预失真效果。

2 2-LMS 算法提出

设预失真系统输入为x(n)，系统待识别模型最优权系数为wopz(n)=[w0,w1,w2,…,wN]，系统的目标输出为d(n)，迭代更新权系数为w(n)。系统迭代更新误差ε(n)为：

设代价函数J[w(n)]为：

基于文献［1］对式（2）进行梯度运算，可得：

式中：t为二范数约束项与迭代误差的调节因子；μ为步长因子；l[w(n)]为更新迭代式中附加项函数。在梯度运算中，可将由文献［2］可得l[w(n)]为：

根据步长因子μ(n)与迭代误差ε(n)之间的关系，设计一种新的步长迭代式为：

为了提高抗噪性能，用ε(n)ε(n-1)代替ε2(n)。

2.1 2-LMS 算法性能分析

首先，对算法的收敛性能进行分析。令p(n)=wopz(n)-w(n)，即迭代权向量w(n)与最优权向量wopz(n)之间的差值。对等式两端同时求期望，可得：

式中，Q为酉矩阵，Λ=diag[λ1…λn]。由LMS收敛条件可知，给出的步长上界非常宽松，根据文献［14］可得：

式中，σ2x表示输入信号的功率，N为输入信号长度。由于本文算法只是在原有最小均方算法基础上调整了步长的迭代公式，故式（7）对2-LMS算法同样适用。

其次，对算法的抗噪性能进行分析。算法实际迭代误差ε(n)为：

式中，ζ(n)表示均值为0、具有平稳分布的高斯白噪声，且与x(n)相互独立，可得：

可知，E[ε2(n)]与E[ε(n)ε(n-1)]相比多了一个E[ξ2(n)]，造成算法易受到噪声干扰不易收敛。

2.2 2-LMS 算法计算步骤

初始化μ(0)、w(0)，输入数据x(n)、d(n)，设定参数a、b，之后按如下步骤进行计算。

步骤1：根据矩阵运算特点计算出实时输出y(n)=xT(n)w(n)；

步骤2：计算实时迭代误差ε(n)=d(n)-y(n)；

步骤3：根据迭代误差的变化，计算步长因子μ=barcot2[aε(n)ε(n-1)]；

步骤4：代入权系数更新式w(n+1)=w(n)+με(n)x(n)+l[w(n)]；

步骤5：代入权系数更新式w(n+1)=w(n)+με(n)x(n)+l[w(n)]，若n≠N，则继续从步骤1 开始循环迭代，直到算法收敛产生最优权系数wopz(n)并输出。

3 2-LMS 算法在数字预失真应用

预失真直接学习结构形式较为简单，算法在收敛情况下能够取得较好的预失真效果，但收敛速度较慢，易受噪声干扰产生波动［16］。基于2-LMS 算法的数字预失真系统能够提高识别预失真器模型的速度和精度，优化整个系统的预失真结果。

预失真器模型采用多项式模型，是Volterra 级数模型的一种简化模型，即去掉了Volterra 级数中不同延时的交叉项，只保留了级数的对角项。由于偶数阶项产生的谐波分量都落在了通带外，因此它只保留了奇数项［17-18］。

2-LMS 算法通过不断迭代更新权向量，对未知的预失真器模型进行辨识，并使功率放大器达到最优输出，具体实现结构如图1 所示。

在多项式模型中，输入信号为x(n)，经延迟后为x'(n)，预失真器权向量为w(n)。y(n)与预失真实时输入信号x(n)的关系可以简化表示为：

式中，z(n)为后置反馈输入信号即预失真系统输出信号；G为功率放大器增益。

式中，z'(n)为功率放大器在理想线性增益下的输入信号，即算法中的d(n)；ε(n)为迭代误差。引入2-LMS 算法权向量更新式如式（5）所示。

4 仿真结果分析

为了验证2-LMS 算法在预失真系统中的应用效果，将2-LMS 算法放入预失真系统中在MATLAB进行仿真验证，并分别与基于LMS、NLMS 及ALMS的预失真系统进行对比。本次预失真系统输入采用的是MATLAB 生成的带宽为180 MHz、64QAM调制的信号，样点数为31 000。2-LMS 算法中，a=800，b=0.02。选取归一化均方误差（Normalized Mean Square Error，NMSE）、误差向量幅度（Error Vector Magnitude，EVM）以及邻道功率泄露比（Adjacent Channel Power Ratio，ACPR）等 指 标进行比较分析，结果如表1 所示。结果显示：基于2-LMS 算法的数字预失真系统在迭代173 次后收敛，明显快于其他3 种算法；NMSE值优化到了-53 dB。与其他3 种算法相比，预失真器能够更加精确地识别功放的逆模型。

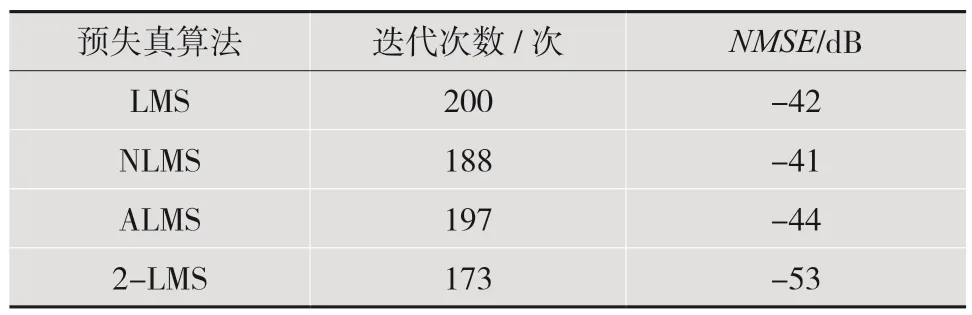
表1 不同算法性能比较

为了进一步验证2-LMS 算法的抗噪性能，实验中将会在收敛到500 次时加入突变。由于传统的LMS 算法与NLMS 算法本身不具有抗噪能力，故不纳入对比。加入突变后的算法收敛，如图2 和图3 所示。在信噪比SNR=25 dB 时，两种算法起始阶段都能够快速收敛，当加入突变后，2-LMS 算法能够快速收敛到原有的稳态误差水平并保持稳定，而ALMS 算法则收敛速度变慢且在收敛过程中产生震荡，无法恢复到原有的稳态误差水平；在信噪比SNR=55 dB 时，2-LMS 算法比ALMS 收敛速度更快，且稳态误差也略低于ALMS 算法。

矢量误差幅度（Error Vector Magnitude，EVM）即信号带内的矫正效果。为进一步验证2-LMS 算法性能，将各个算法在不同噪声环境下进行仿真实验。仿真实验中，在输入信号加上高斯噪声或高斯噪声和脉冲噪声的混合噪声，并在不同信噪比环境下对比EVM值，结果如表2 所示。在高斯噪声中，SNR=20 dB低信噪比环境下，基于2-LMS算法的EVM值比LMS 算法减少了4.5%；在高斯噪声中，SNR=50 dB 高信噪比环境下，基于2-LMS算法的EVM值比基于LMS 的减少了2.6%；在混合噪声中，SNR=20 dB 环境下，基于2-LMS 算法的EVM值比基于LMS 算法的EVM减少了7.5%，比基于ALMS 算法的EVM减少4.9%；在混合噪声中，SNR=50 dB 环境下，基于2-LMS 算法的EVM值比LMS 算法减少了5.1%，比基于ALMS 算法的EVM减少2.9%。

图4～图7 为4 种算法的预失真频谱图。可见，基于2-LMS 算法的数字预失真系统能够更加精确地识别功率放大器的行为逆模型，数字预失真能够有效地抑制带外频谱泄露和带内失真，改善功放的线性化程度。另外，带外抑制与ALMS、NLMS、LMS 相比，分别降低了约6 dB、9 dB、10 dB。

邻道功率比（Adjacent Channel Power Ratio，ACPR）指相邻信道与主信道功率之比，即预失真系统带外校正效果。不同算法下，预失真系统邻道功率比结果如表3 所示。可见，改进的2-LMS 算法与其他算法相比有着较好的带外抑制频谱扩展的效果，ACPR值均有优化。与基于LMS 预失真系统相比，ACPR值改善了-10.3 dB；与基于ALMS的预失真系统相比，ACPR值改善了-7.6 dB。

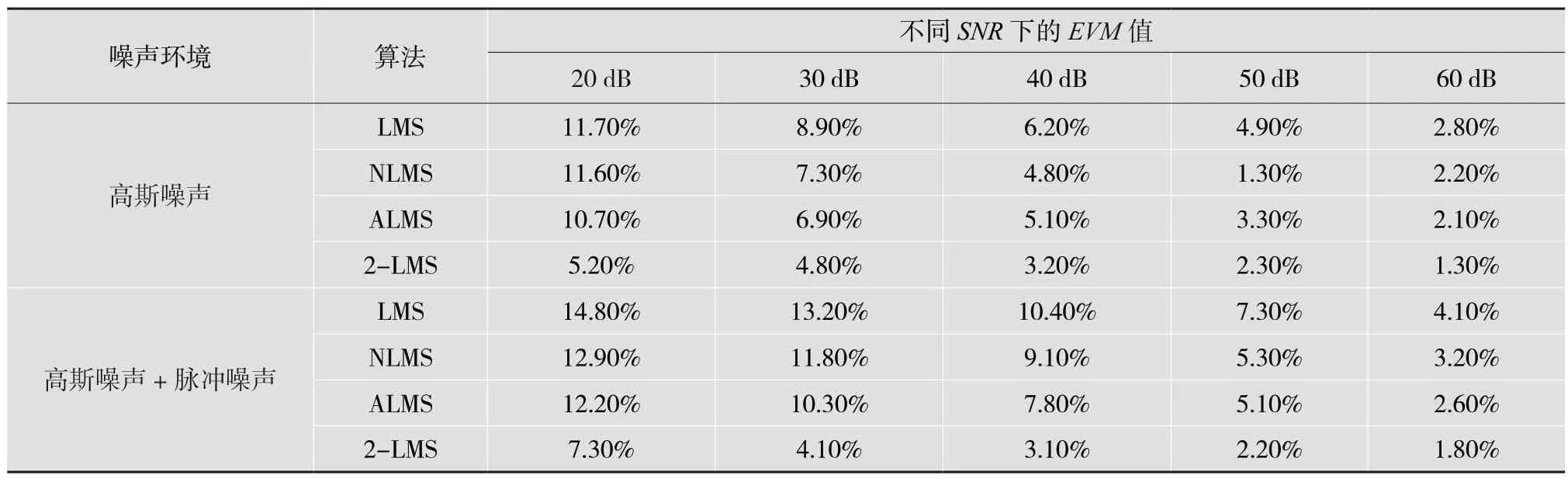
表2 各种算法在不同噪声环境下EVM 对比

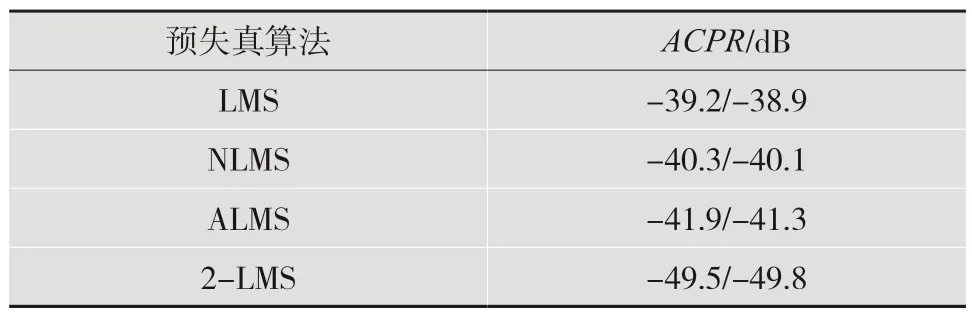
表3 不同算法下预失真系统ACPR 对比

为了验证2-LMS 算法在具有一定稀疏性系统中的收敛性能，分别将两种算法放入具有稀疏性系统中进行比较。此次预失真器模型选用记忆多项式模型，记忆深度为3，非线性阶数为10，全模型参数个数为40 个，稀疏度为6/40。具体对比结果如图8 所示。由于基于ALMS 算法时没有考虑到稀疏特性，故算法的性能大大降低，约在3 170 次时开始收敛，而基于2-LMS 算法大约在2 000 次开始收敛，且与基于ALMS 算法相比降低了稳态误差。

5 结语

本文介绍了2-LMS 算法并根据其特点应用于数字预失真直接学习结构中。2-LMS 算法具有收敛速度快、识别行为模型精度较高以及抗噪能力较强的优点，克服了传统自适应算法收敛速度慢且易受噪声影响产生波动的缺点。仿真实验结果表明：基于2-LMS 算法的数字预失真系统和原基于LMS预失真系统相比，ACPR优化了-10.3 dB；在低信噪比混合噪声环境下的EVM指标优化了7.5%，较好地补偿了功放输出的非线性失真；同时，在系统呈现一定的稀疏性时，2-LMS 算法也能够保持良好的性能。