控制算法理论及网络图计算机算法显示研究

杨静

摘  要：网络图在民众平日生活中扮演着重要的角色，在电力网络的运用阶段，把其拓扑为电脑对讯息的接纳的情况很多。研讨控制算法学说与网络图电脑算法显示，通常要对图的储蓄构造实施解读，融合网络图显示屏上的显示模式，构建网络图显示与检索平台。在计算机算法中融合图论观念，能够对网络图实施构建，鉴于网络图的计算机算法具备很多优势，不但能够将人工绘图与计算时间缩减，并且能够提升生产效率。

关键词：控制算法  网络图  电脑算法  实例解析

中图分类号：TP13                             文献标识码：A文章编号：1674-098X（2020）09（b）-0118-03

Absrtact： Network graph plays an important role in people's daily life. In the application stage of power network， there are many cases that the topology of network is the acceptance of information by computer. In order to discuss the control algorithm theory and network graph computer algorithm display， we usually need to interpret the savings structure of the graph， integrate the display mode of the network chart display screen， and construct the network chart display and retrieval platform. In the computer algorithm， the concept of graph theory can be used to construct the network diagram. In view of the advantages of the computer algorithm of network graph， it can not only reduce the time of manual drawing and calculation， but also improve the production efficiency.

Key Words： Control algorithm; Network diagram; Computer algorithm; Case analysis

邁入新世纪后，科技的飞跃带动了当代化进程的快速实现，电脑科技的普及运用，带动了各领域的进步。电脑科技与图论将的高效结合，不但体现了定量上的技术，并且也会在定性解读方面提供巨大的帮助。网络图电脑算法的显示流程也是融合控制算法学说与网络图的重要部分，其体现了当代化电脑算法显示的特征。所以，笔者对控制算法学说与网络图电脑算法显示的研讨不但能够帮助经济发展，并且有着极为重大的价值。

1  电脑网络图的显示原理与储蓄构造简析

电脑网络图的显示原理简要来讲就是点与线的对接。例如，假如需要化解一个难题，就需要从难题的特征入手。唯有对难题的根由实施解读并研究出难题形成的主因，才能用最高效的模式来化解该难题。例如，进行换位思考，把数学方面的难题使用数学学说建立模型，使用这类建模的模式对难题实施分解，就会发觉全部难题在数学模型中都体现为点与线。而最初的数学建模的创意，是数学家们通过国际象棋的下法中提炼出的。在国际象棋竞赛的阶段，参赛人员必须依照竞赛规则依序在两大相异的方位安放皇后。而且棋手挑选皇后的方位有两大准则，这两大准则是：首先，走位最少的;其次，是走位最多的。而通过这类模式就组成了电脑网络图中最简单的数学模型。而且，因为电脑网络图最核心的部分就是点与线，因此图像的行业为电脑网络图最为重要的组成模式。在后期数学家的研讨中，数学家把图论结合到电脑算法中，能够使用控制算法对难题实施分解。通过这类模式构成的电脑网络图能够把图论中的数学模型与理论系统实施结合，从而加强运算效果。

在最原始的电脑运算阶段的储蓄构造一般是通过关联矩阵发挥功能的，对接矩阵、十字对接表、对接表是基本的组成要素。而且，关联矩阵构造与邻接矩阵构造通常是以数组来显示的。十字连表与邻接表通常体现了链表构造间的关联。而且在电脑计算阶段的储蓄构造中链接表的模式并非单纯限于一类。一般地，数学家透过对接表节点，并在对接过程中依序表述邻接表算法，就能够更有效地在网络图内对既有的电脑算法实施表述。

2  网络图的显示分析

网络图的电脑显示学说通常要融合C语言完成网络图的编绘。在网络图点之间的连线解读阶段，通常有着极为繁杂的顶点与变的关联，并在荧屏的网络图编绘中把各个顶点绘出，物理坐标轴表示见图1。

在x轴与y轴的运算阶段，更应确保数据是整数。透过在荧幕上勾边，在明确顶点坐标，荧幕上对顶点的任意增加中，必须完成方法的基本编绘。

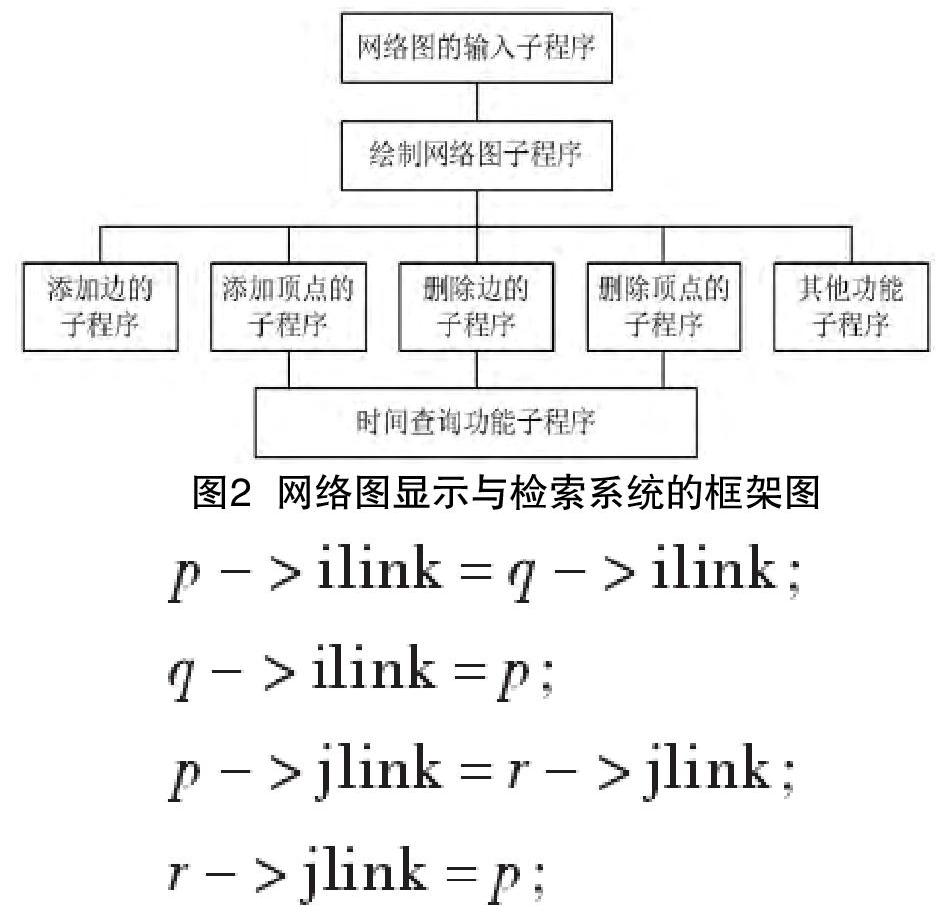
图的显示算法计算中，透过对网络图的编绘，把几条边与顶点进行勾画，把一些边与顶点剔除，并在历史检索中对时间实施存档并记载。网络图显示与检索系统的基本框架见图2。

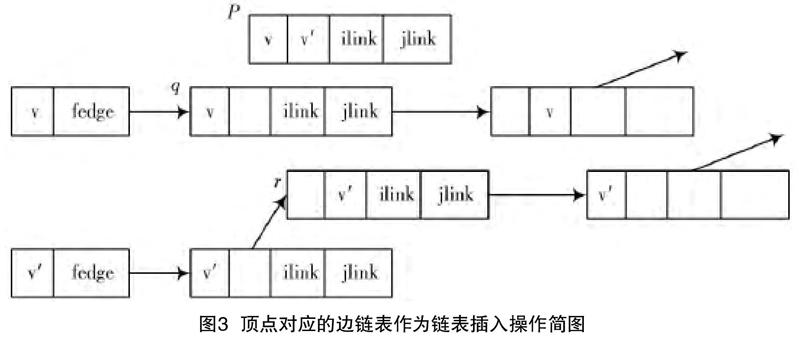
网络图显示的算法融合中，通过绘出网络图，且在网络图有关讯息录入阶段，对邻接多重表实施修复，有关新添加的顶点把其标注为visited，并且也为ture。新的边节点出现以后，在图中P方位的对接中，把新添的边的顶点明确，见图3。具体操控是：

网络图显示阶段牵涉到的一部分功能算法的完成必须融合辅助性的功能绘出网络图并进行网络图的矫正，第一时间储蓄网络图，并对其边与有关顶点进行增加，完成图形的显示，从而建立网络图电脑显示与检索的基础系统。

3  網络图电脑算法与现实模式详解

在当代化网络图的普及运用中，融合电脑算法与具体的显示流程不单存在点符号全控制一类算法，并且也有边符号控制算法。针对网络图的显示模式来讲，必须进行多元化显示模式的探索与创新。

3.1 点符号全控制算法

点符号的原理，通常融合了全控制算法的演变过程。这类符号全控制算法在有关学说中，是融合符号控制算法实现的，是鉴于该领域的组织结构，在符号全控制算法中引进极限度，并完成最大最小度的设定，这类网络图的符号控制算法下限阶段，完成下限间的根本更新流程。在符号全控制算法图像的显示中，融合边限问题的更新角度，对下界的具体网络图实施根本上的满足。网络图符号的全控制算法中，确保符号具备既定的完备性与全面性极为关键还。网络图算法的研讨，要创新思维，完成算法。

3.2 边符号控制算法

2001年符号边控制算法诞生，其在m边的最小符号边控制算法的明确中，完成了网络图控制算法理论内容的充实与健全。2002年，网络图的符号控制算法在对上界与下界的明确中，融合特别网络符号边控制算的准确数据，完成了网络图边控制算法的边限的确定工作。

3.3 网络图的显示模式

对符号与边符号的显示来讲，透过融合网络图的一类显示模式，在荧幕对有关网络图的编绘阶段，就应完成数值的录入与点的增添。数值的录入，必须让运用者把命令在电脑录入网络图中录入，并对有关数值讯息实施录入。这类有关参数的讯息，不但包含顶点的数目N，并且也包含边的数量M与顶点的坐标。透过对邻接多重表实施建立，在邻接两重表中录入数值，从而让网络图的数值输出能够进行。这类对边与顶点的录入阶段，完成边与顶点命令的增添并输入新增添的数量。顶点新增添的阶段，通常是独立运作的。在网络的不完全接通中，通常要进行基础性的工作，完成网络图的基本管控。所以，在网络图电脑算法与显示中，以点符号全控制算法与边符号控制算法为基准，在网络图控制算法使用阶段，完成网络图的创新性设计，实现电脑算法与显示系统的高效工作。

4  具体实践中电脑算法与显示模式的改善策略

当代生活的各个行业中，网络图的普及使用带动了当代社会的进步。对电脑网络图中的符号全控制来讲，融合边符号控制体系的健全，对电脑的显示实施管控，完成检索与显示相融合的网络图的构建工作。

电脑算法与显示中，融合网络图显示与有关的检索系统，在系统的不稳定预设中，重视系统内网络图的多重矫正。通过对顶点与边的反复校正，这类多回合的校正完成了数据的及时检索，不但把图像的呆板特征弱化，并且也规避了图像的不清楚的情况过于频繁地出现。融合数据库的模式，在数据库内对有关数据实施调整，把数据检索的基础需求进行满足，完成对系统的调整。在相异对象的解读中，完成系统化矫正极为关键。鉴于在交通网络中的运用，让电脑算法与显示模式更为高效。

5  结语

总之，基于网络图的电脑算法是中国社会发展到一定阶段的必然结果，所以有关机构要高度关注。应充分地解读网络图的有关论述，之后从点符号全控制算法、边符号全控制算法两个层面对目前网络图计算机算法实施解读;要创新思维、发散思维。

参考文献

[1] 李晶，汪晓飞，段新娥.基于BP神经网络和蚁群算法的机械手轨迹控制算法研究（英文）[J].机床与液压，2019，47（24）：146-152.

[2] 李红斌，王嘉伟，张晶晶，等.提高能效的自主供电系统智能控制算法模型建立与仿真[J].现代电子技术，2019，42（24）：183-186.

[3] 王鑫，张青，王银，等.基于遗传算法的差速耦合式混合动力系统模糊控制策略优化[J].动力系统与控制，2019，8（2）：81-93.

[4] 张明明，刘维亭，魏海峰，等.基于滑模观测器的PMSM单相霍尔位置传感器故障容错控制算法[J].水下无人系统学报，2019，27（6）：651-657.

[5] 白洁，王胜.采用改进粒子群算法的优化电液无凸轮气门机构控制研究[J].中国工程机械学报，2019，17（6）：515-518，522.

[6] 殷婷婷，贾方秀，于纪言，等.基于改进LuGre摩擦模型的双旋弹丸固定舵翼滚转位置鲁棒自适应控制算法[J].兵工学报，2019，40（12）：2425-2432.