风力发电机组发电能力评估优化方法

2020-02-22张世磊

科技创新导报 2020年25期

张世磊

摘要：为了提高评估风力发电机组（以下简称风机）发电能力的准确性以提高风机的利用小时数，本文采用稳定工况判断和机头微气候环境温度修正厂商担保功率曲线建立风机实际功率曲线模型，对1台1500kW风机的运行数据进行数值模拟计算，得出风机在不同温度区间的实际功率曲线和修正厂商担保功率曲线的功率分布，计算风机的功率绝对误差和功率一致性系数，并给出风机的运行优化建议。结果表明：风机机头的微气候环境温度对风机的功率影响较大，采用修正厂商担保功率曲线、分温度区间进行计算的方式能够提高风机发电能力评估的准确性。

关键词：风力发电机组环境温度功率曲线发电能力

中图分类号：TM315 文献标识码：A 文章编号：1674-098X（2020）09（a）-0037-06

Abstract：In order to improve the accuracy of evaluating the power generation capacity of wind turbine （hereinafter referred to as wind turbine） and improve the utilization hours of wind turbine， the actual power curve model of wind turbine is established by using stable condition judgment and microclimate environment temperature correction manufacturer guarantee power curve at the head of the fan， and the operation data of one 1500kW fan is calculated by numerical simulation， and the actual power curves of the fan at different temperature ranges and the power distribution of the modified manufacturer's guaranteed power curves are obtained. The absolute power error and power consistency coefficient of the fan are calculated， and the operation optimization suggestions of the fan are given. The results show that the microclimate environment temperature of the fan head has a great influence on the power of the fan， and the accuracy of the evaluation of the power generation capacity of the fan can be improved by modifying the guaranteed power curve of the manufacturer and calculating by temperature range.

Key Words：Wind turbine generator; Ambient temperature; Power curve; Power generation capacity

經过近些年风电项目的开发与发展，我国风电装机容量已经十分巨大，风电的迅猛发展无疑带来了巨大的机遇，但同时也带来了巨大挑战，已建成风电场实际运行和经济效益存在一定的问题。风机发电能力评估是指对已经投产运行风机的功率曲线进行的系统、客观的量化分析和评价。通过风电能力评估，确定风机目前运行的健康水平，为风机后续的运行和检修提供数据支持。风机的发电能力直接影响发电量，进而影响风电场的整体生产经营指标。风机的运行实际功率曲线可以反映机组的实际发电能力与机位的微气候条件，对机组运行和检修具有重大意义。目前行业内功率曲线的计算方法有：测风塔数据外推法、样板机法、机头风速法等，工程使用效果不太理想，均未考虑风机机头所在微气候环境参数的影响，尤其冬夏温差大和山地风场更为明显;如何利用风机机头微气候环境温度修正厂商担保功率曲线并对风机实际功率曲线进行建模，作为风机发电能力计算的依据，则正是本文要研究的内容。

本文以内蒙某风场1500kW风机为研究对象，根据现场实际生产运行数据，对冬天和夏天两种气候环境下的实际功率曲线进行了数值研究，并对厂商担保功率曲线修正前后的情况进行对比。

1 基本信息

1.1 功率曲线

功率曲线指风力发电机组输出功率和风速的对应曲线。描绘风电机组功率输出与风速的函数关系图和表。风机在运行过程中，功率时刻随着风速的变化而变化。功率曲线作为反应风机性能的重要数据，已经开始引起新能源发电行业的重视，功率曲线验证作为一项新的课题，摆到了风电技术人员面前。国内的一些领先企业已经开始从事功率曲线验证的研究性工作，这将为风机的参数校验带来科学的依据，会给风电场的发电量带来很大的提高。

目前国内大部分风机制造商提供的担保功率曲线是通过设计仿真计算出来的标准空气（大气压力为101.325kPa，温度为0℃，相对湿度为50%）下的风速功率关系曲线，但由于机头微气候环境温度因素的影响，风机在不同微气候环境的担保功率曲线会存在差异，因此需要进行修正。

1.2 风机稳定工况定义

因风机的惯性较大，功率的变化不能实时响应风速，功率存在时滞性，将t时刻风机稳定工况定义为：[t-2min，t]时间之内风速Vmax-Vmin<2m/s且功率Pmax-Pmin<20%P容量，工况风速V工况定义为：[t-1min，t]时间范围内风速历史数据的加权平均值，工况功率P工况定义为：[t-1min，t] 时间范围内功率历史数据的加权平均值，工况温度T工况定义为：[t-1min，t]时间范围内环境温度历史数据的加权平均值。

1.3 空气相对湿度对空气密度的影响

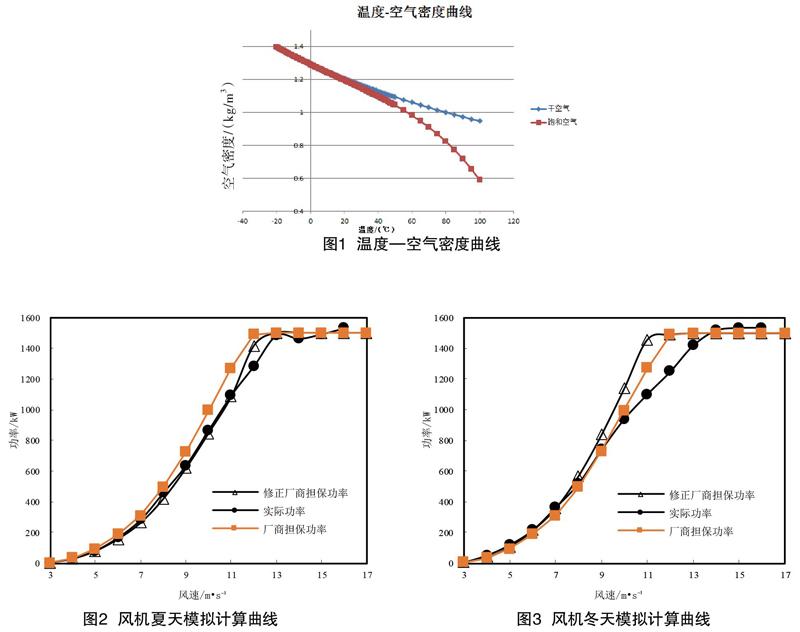
标准大气压下，在温度范围为：-20～100。C ，干空气密度和饱和空气密度的对比曲线如图1所示。

图1为空气相对湿度为干空气和饱和空气下的空气密度与温度对应关系，通过上图可以看出，气温50。C 以下，干空气和饱和空气的空气密度偏差均小于0.05 kg/m3;气温40。C 以下，干空气和饱和空气的空气密度偏差均小于0.031 kg/m3;风机运行环境的空气温度一般低于40℃，在该温度范围下，空气相对湿度的影响较小，故本文研究忽略空气湿度的影响（采用相对湿度为50%状态下的数据）。

1.4 二维插值法

利用微气候空气密度和风速结合担保功率曲线，通过二维插值法计算风机理论功率。

空气密度插值：若当前空气密度不存在，则利用相邻空气密度曲线功率进行插值得出该空气密度下的担保功率曲线;若大于最大或者小于最小空气密度则选用相应最大最小理论功率。

风速插值：基于该空气密度下的擔保功率曲线，利用相邻风速进行插值得出该风速下的理论功率。

2 数学模型及计算方法

2.1 数学模型

2.1.1 微气候空气密度模型

标准大气压下，气温40℃以下，干空气密度与饱和空气密度偏差均小于0.031kg/m3;风机正常运行环境的气温低于40℃，在该温度范围下，本文研究忽略空气湿度的影响。

相对湿度取标准空气的相对湿度0.5，空气密度计算公式可以简化为：

式中，ρ为空气密度，kg/m3;B为大气压力，Pa;t为气温，单位为℃。

根据大气压力与海拔高度的经验公式：

式中，H为海拔，m。

2.1.2 风速修正模型

风机机头风速由测风仪测得，当前风机测风仪分为两种，一种是传统风杯测风，另一种是激光装置测风。风速仪安装在风轮后面，为做功后的风速，功率曲线的风速为做功前的风速，为得出相对准确的风速数据，根据能量守恒近似计算风轮前风速，传统风杯测风计算公式如下：

式中，Vf为风轮前风速，m/s;ρ为空气密度，kg/m3;P为风机功率，kW;V为当前风机风杯测得的风速;R为风机风轮半径，m。

2.2 计算方法

2.2.1 修正厂商担保功率曲线

厂商一般会给不同空气密度下的担保功率曲线数据，通过风机机头微气候空气密度利用插值法对担保功率功率曲线进行修正，根据计算得到的微气候空气密度ρ寻找厂家提供的2条空气密度相邻的担保功率曲线，满足ρ1<ρ<ρ2，修正计算方法可表示为：

式中，ρ1，ρ2为空气密度，kg/m3;P1，P2为担保功率，kW;PL为修正担保功率，kW。

2.2.2 计算机头微气候理论功率

对工况风速通过公式（3）进行风速修正，利用风机工况温度和机海拔通过公式（1）计算微气候空气密度，利用厂商担保功率曲线和微气候空气密度通过公式（4）修正担保功率曲线;基于修正担保功率曲线进行功率插值计算得出机头微气候理论功率P理论。

2.2.3 建立风机实际功率曲线数据模型

当工况功率P工况在0.7P理论～1.3P理论之间，则认为风机处于非限功率正常发电状态，数据判定为有效工况功率。

2.2.4 风机发电能力评估

通过计算一段时间内某个温度范围内的实际功率曲线与厂商担保功率曲线的偏差，评估风电机组的发电能力。

在厂商担保功率曲线的风速点上，选取切入风速和切出风速区间以1m/s为步长的若干风速点及各风速点对应的有效工况功率和微气候理论功率，计算功率一致性系数和功率绝对误差，以此评价风机的发电能力。

功率绝对误差：

功率一致性系数：

式中，PMAE为功率绝对误差;为功率一致性系数;P工况i为i风速点有效工况功率，kW;P理论i为i风速点微气候理论功率风速，kW;n为风速点数量;V切入为风机切入风速，m/s;V切出为风机切出风速，m/s。

功率绝对误差为负值表明风机发电能力低于厂商担保功率曲线，为正值表明风机发电能力高出厂商担保功率曲线;当功率一致性系数低于规定值95%则表明风机发电能力出现较大偏差，应安排联系技术人员及时进行巡检。

3 实例分析

选取内蒙古某风场1500kW风机作为研究对象，分别抽取同一台风机2018年夏天7～8月和2018年冬天11月～2019年1月的历史数据进行筛选预处理和计算，对同一风速点附近的数据进行合并。该风机的厂商担保功率曲线为标准空气密度1.293kg/m3下的数据，标准空气密度为大气压力101.325kPa、环境温度温度0℃、相对湿度50%条件下的空气密度。

表1为2018.7.1-2018.8.31期间某风机的运行数据，数据包括厂商担保功率、实际功率和平均环境温度。

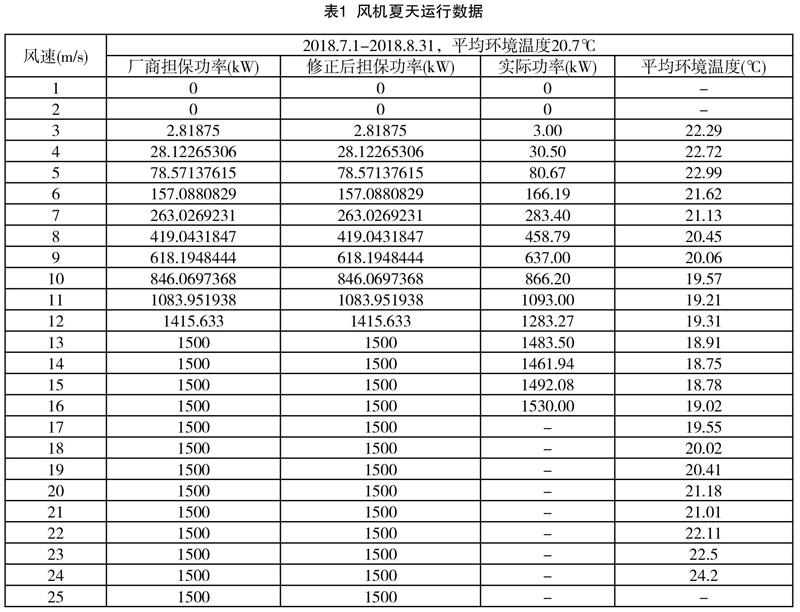
从图2风机夏天实际功率、厂商担保功率和修正厂商担保功率与风速关系的模拟计算曲线，可以看出，由于夏天环境温度（平均20.7℃）较高、风功率密度较低，修正后担保功率低于修正前，修正前功率绝对误差为-52.65kW，功率一致性系数为89.84%，低于规定值95%;修正后功率绝对误差为-3.07kW，风机的功率绝对误差明显降低，功率一致性系数为95.55%，高于规定值95%，修正后风机发电能力评估处于正常范围，无需加强风机的定检和分析大部件的运行情况。通过修正前后对比可发现，夏天风机的厂商担保功率会下降，风机的实际发电能力也偏低，若实际功率曲线在修正厂商担保功率曲线和原厂商担保功率之间则会存在误判异常的情况。

表2为2018.11.1-2019.1.31期间某风机的运行数据，数据包括厂商担保功率、实际功率和平均环境温度。

从图3风机冬天实际功率、厂商担保功率和修正厂商担保功率与风速关系的模拟计算曲线，可以看出，由于冬天温度（平均温度-7.1℃）较低、风功率密度较高，修正后担保功率高于修正前，修正前功率绝对误差为-21.74kW，功率一致性系数为87.61%;修正后功率绝对误差为-66.00kW，风机的功率绝对误差明显增加，功率一致性系数为88.13%;修正前后风机冬天功率一致性系数均低于规定值95%，均处于亚健康状态，应加强风机的定检和分析大部件的运行情况。通过修正前后对比可发现，冬天风机的厂商担保功率会上升，风机的实际发电能力也偏高，若实际功率曲线在修正厂商担保功率曲线和原厂商担保功率之间则会存在误判正常的情况。

4 结语

本文对风机引入稳定工况的判断、利用风机机头微气候环境温度修正厂商担保功率曲线、并对机头前风速进行修正、对风机实际功率曲线进行建模，得到提高评估风机发电性能准确性的方法。通过对机头风机发电能力评估模型建立和计算，可以得到以下结论：

（1）引入稳定工况可以排除复杂风况环境、调度限功率等条件下的影响，利用风机机头微气候环境温度参与计算可以达到消除空气密度的影响。

（2）修正前后担保功率偏差较大，影响风机功率绝对误差和功率一致性系数数据的计算结果。通过实例数据分析验证，发电能力的评估效果较好，得到提高评估风机发电能力准确性的方法。

（3）本文的评估优化方法能够提高风机发电能力评估的准确性，对正确评估分析风机发电能力、主动发现风机的亚健康运行起到积极作用，更好的指导风机运维和检修，对于提高风机的发电量和利用小时、挖掘风机发电潜力、提升发电企业收益具有积极意义。

实际工程实践过程中有些风机厂商存在无法给出不同空气密度下厂商担保功率曲线的情况，会影响修正过程，最终影响评估风机发电性能的准确性。

参考文献

[1] 姜文玲，王勃，汪宁渤，等.多时空尺度下大型风电基地出力特性研究[J].电网技术，2017（2）：163-169.

[2] 王錚，刘纯，冯双磊，等.基于非参数回归的风电场理论功率计算方法[J].电网技术，2015，39（8）：2148-2153.

[3] 范奇，王曦，孙志超，等.基于实时功率曲线的风电机组出力特性研究[J].节能技术，2019，12（6）：557-560，570.

[4] 郭海思，何慧，包大恩，等.风电机组理论发电功率计算及对比优化[J].电力与能源，2019，40（3）：339-343.

[5] 许佳妮，高峰. Wind turbine static yaw error detection based on optimal tip speed ratio[J]. 电力科学与工程， 2019，35（5）：37-42.