基于流固耦合的环模成型机关键部件疲劳寿命分析
2020-02-22李震王鹏刘彭高雨航王宏强
李震,王鹏,刘彭,高雨航,王宏强
(内蒙古科技大学机械工程学院,内蒙古 包头 014010)
生物质是指利用光合作用而形成的各种有机物体,也是一种无污染的可再生能源[1]。但因具有松散和密度较小等特性,使其难以运输和储存,研究生物质成型压缩技术可以提高其运输及存储能力,并具有一定的经济效益。生物质成型压缩是将松散的生物质挤压成具有一定形状的凝聚态固体燃料的技术[2]。环模成型机因其具有高产、优质和高效等特点,是生物质成型的主要加工设备。目前,环模成型机还存在着平均使用寿命短和制造成本较高等方面的问题。环模成型机的核心部件是环模和压辊,环模和压辊的使用寿命取决于环模和压辊的强度、刚度与疲劳寿命[3]。因此,对环模和压辊进行疲劳分析、强度校核具有十分重要的意义。已有国内外学者对环模成型机所受应力与疲劳寿命进行了相关的研究。Celik 等[4]提出了一种有限元分析的方法,通过控制长径比与压力的关系使得压辊式成型机的寿命得到提高。陈树人等[5]通过对立式秸秆环模成型机磨损后的环模进行测量分析,发现磨损沿着秸秆挤压方向逐渐减弱。李震等[6]就环模模孔形状结构对模孔磨损及疲劳破坏的影响进行了研究,结果表明,环模锥角大小及进料腔的长度都会对环模模孔所受应力产生重要影响,并找到了最优参数尺寸,为环模结构优化提供了依据。蒋清海等[7]对环模进行磨损试验,从环模及模孔内壁的磨损量可知,环模内壁主要以疲劳磨损为主,磨损量大于模孔内壁磨损。王慧等[8]运用雨流计数法和COSMOS 软件对不同参数条件下的环模疲劳寿命进行分析,并根据疲劳寿命对环模参数进行优化。
传统方法对环模所受应力及疲劳寿命进行分析主要通过对环模压辊施加均布载荷,但是物料在成型过程中处于低应变频率时,黏性系数较小,容易流动,表现出流体的运动特性,随着应变率的增加,其黏性系数逐渐增大,又呈现固体结构特性[9]。这就导致物料与环模和压辊之间的作用力不是均布载荷,从而会导致最后所得结果与实际过程产生误差[10]。为减小数值仿真的误差,笔者通过流固耦合方法对环模成型机所受应力及疲劳寿命进行了分析。
1 环模成型机几何结构及尺寸
当环模成型机中的物料处于楔形区域时,物料会受到来自环模与压辊的攫取力,控制物料的成型,此时多排模孔之间流体的相对影响可以忽略。因此,可以采用单排模孔进行分析,以减少模拟时间,提高运算效率。环模成型机结构尺寸如图1a所示,采用的生物质原料为沙柳细枝颗粒,整个模型分为环模和压辊,最小模辊间隙为2 mm,模孔的长径比为6∶1,模孔锥角20°。根据以上尺寸运用Solidwork 软件对环模压辊进行建模,得到如图1b所示的三维模型。

图1 环模压辊结构尺寸和几何模型Fig.1 The structural dimensions and geometric model of the ring mold and pressure roller
2 流固耦合分析方法
采用流固耦合分析方法对环模成型机结构进行应力分析,首先应用Fluent 软件对成型机内物料流动的流体域进行仿真,然后采用Workbench 软件流固耦合模块对环模成型机固体域进行分析求解。
2.1 流体域分析
物料在致密成型过程中首先表现为连续性介质,从而可将物料看成由一系列的质点和微团堆积组成的一个多质点体系。这一体系质点和微团在运动过程中均遵循均匀和连续性特点,而该体系中蕴含的应力、应变和位移等物理量也有着相同的均匀和连续性特点,从而使物料在致密成型的流动过程中满足质量守恒、动量守恒和能量守恒定律。因此,可以通过流体力学理论与有限元方法对物料成型过程进行分析。
本研究中的生物质物料在环模旋转的带动下产生运动,在变形压紧区内产生湍流流动。因此,采用连续相计算时以标准k⁃ε湍流模型进行计算。
湍流动能方程(k方程)为:

耗散方程(ε方程)为:

式中:ρ为流体密度;μ为黏度系数;μi、μj为xi、xj方向的速度;xi、xj为坐标位置;t为时间;Gk为由平均速度梯度产生的湍流动能,按照k模型中的紊流模型的建模计算;Gb是因浮力而产生的紊流动能,根据浮力效应计算k模型的湍流;YM为波动膨胀的变化和可压缩湍流对整体耗散的速率,按照可压缩性对k⁃κ模型湍流的影响进行计算;C1ε、C2ε和C3ε为常数;σk和σε为湍流动能κ和耗散率ε对应的普朗特常数;Sk和Sε为自定义参数。根据模型常量,设置C1ε=1.44、C2ε=1.92、C3ε=0.09、σk=1.0、σε=1.3。
2.1.1 流体域网格划分及求解设置
运用Geometry 软件对流体域进行抽取,如图2a 所示,并对其进行网格划分。由于采用结构网格对物料流场进行网格划分时模孔处存在倒角且尺寸较小,网格划分后质量不高,且计算周期较长。因此,采用非结构网格对其进行网格划分。通过非结构网格以及边界层网格处理划分后,得到内流道网格数量约为56 万,如图2b 所示,网格质量较好且无负体积,可导入Fluent 软件进行运动仿真。

图2 流体域及内部流动网格Fig.2 The fluid domain and its inner flow grid
入口边界(环模正上方)设置为质量入口(mass⁃flow inlet),质量流率为0.18 kg/s;出口边界(环模模孔出口处)设置为压力出口(pressure out⁃let),压力为标准大气压;其余壁面为无滑移壁面(wall),摩擦系数为0.35。仿真选用瞬态计算和k⁃ε湍流模型来模拟生物质颗粒在环模成型机内的运动。密度基求解器适用于高速运动和可压缩流体。动网格基于瞬态计算来进行网格的重构。能量方程和k⁃ε湍流模型让仿真更加接近生物质颗粒在成型机内的真实运动状态。在求解参数设置中,采用适用于可压缩性流动的耦合显式算法Coupled 的数值算法[11]。
采用动网格方法中的光顺方法(smoothing)和网格重构(remeshing)来模拟环模的运动,设置运动区域为刚体运动区域(rigid body),对运动壁面进行用户自定义函数(UDF)编译。通过调用刚体运动宏(DEFINE_CG_MOTION)设置环模转速为32 rad/s,旋转方向为顺时针,模拟环模的转动。
2.1.2 流体域结果
通过计算可以得出环模成型机内物料在成型过程中所受压力分布云图,如图3 所示。从图3 中可以看出,随着模辊最小间隙的逐渐减小,物料所受压力呈现逐渐增大的趋势。物料从模孔入口到出口,受到的压力逐渐减小,在模孔出口处存在压力减压回弹的现象。

图3 流体域压力分布云图Fig.3 Pressure distribution cloud diagram of the fluid domain
2.2 固体域分析
2.2.1 固体域网格划分及约束
环模和模孔均采用非结构网格进行划分。对环模和压辊壁面边界进行边界层网格处理,如图4所示。对环模和压辊工作表面进行边界层处理,以保证在运用k⁃ε模型计算下的计算精度。由于压辊在制粒成型中绕自身中轴旋转而不能进行上下左右移动,因此,对压辊左右壁面施加固定位移约束。由于压辊和环模在旋转过程中会产生一定离心作用力[12],根据环模和压辊旋转方向和物料所受压力大小,在其壁面设置相应的旋转速度为94 rad/s。
2.2.2 流固耦合分析

图4 固体域网格划分Fig.4 Grid division of solid domain
通过Workbench 将Fluent 软件计算结果传递到Static Structural 模块中,在Static Structural 模块中可以通过外加载荷(imported load)将Fluent 软件计算的边界压力数据结果施加到对应的固体壁面边界中,从而得到压辊壁面应力分布图,如图5所示。

图5 压辊应力分布Fig.5 Pressure distribution of pressure roller
环模成型机环模和压辊选用合金结构钢20CrMnTi 为材料,其材料属性如表1 所示。
通过计算可以求得压辊在物料成型过程中,在物料压力和离心力作用下的整体位移变形量及其Von⁃mises 等效应力云图,如图6 所示。
从图6 中可以看出,压辊的最大位移变形发生在压辊和环模的最小间隙处,其最大值为0.608mm。压辊受到的最大应力也发生在此处,为30.50 MPa,而顶部受到的应力相对较小。此处区域压辊的最大位移变形、最大应力和现实生产过程中压辊的变形和受力情况吻合。随着辊轧过程的进行,楔形区内的物料高度逐渐减小,物料所受应力增大,而致密过程主要是靠压辊和环模的挤压[13]。因此,物料提供给压辊的反作用力增大。在最小间隙左端,压辊和环模的间隙逐渐增大,物料挤压力减小,压辊受到的应力也随之减小。从图6 中可知,在环模成型机制粒成型过程中,由于物料挤压力的影响,容易在最小间隙处发生疲劳磨损。同理可以得出环模表面在物料压力作用下的整体位移变形与等效应力云图,如图7 所示。

表1 20CrMnTi 的材料属性Table 1 Material properties of 20CrMnTi

图6 压辊变形图及其Von⁃mises 等效应力云图Fig.6 Deformation diagram and its Von⁃mises equivalent stress cloud diagram of pressure roller
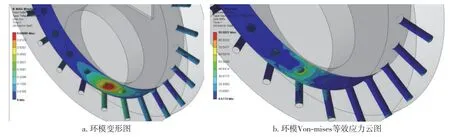
图7 环模变形图及其Von⁃mises 等效应力云图Fig.7 Deformation diagram and its Von⁃mises equivalent stress cloud diagram of ring mold
图7a 中环模壁面最小间隙处的模孔进料端处变形位移达到最大,最大变形量为0.6 mm。图7b中环模壁面最小间隙处模孔进料端处所承受的应力最大,为90.05 MPa。由于压辊和环模的挤压作用,楔形区域的一部分物料被攫取进入到环模的模孔内,剩余物料通过最小间隙且随着环模旋转继续被挤压。因此,环模壁面的最大应力和最大位移变形发生在环模模孔的进料端处,另一端的应力和位移变形相对较小。从中可以得出,在环模成型机制粒成型过程中,环模模孔进料端处容易发生疲劳磨损。
3 环模压辊疲劳寿命分析
在环模成型过程中,物料持续受到环模和压辊的挤压以及摩擦,容易使得环模和压辊周期性地受到疲劳弯曲应力,从而造成环模及压辊发生疲劳破坏。
通过运用Fe⁃safe 软件中的seeger 材料特性估计方法,得出20CrMnTi 材料的S⁃N曲线,如图8所示。
将所得到的S⁃N曲线数据导入Workbench 中的材料参数中,可以分别求得压辊与环模的疲劳寿命云图,如图9 所示。

图8 20CrMnTi 材料S⁃N 曲线Fig.8 S⁃N curve of 20CrMnTi material
从图9a 中可以看出,压辊疲劳破坏主要发生在环模与压辊的最小间隙处,且靠近压辊的两个壁面处疲劳寿命较短,中间部分疲劳寿命较长,压辊的最小寿命6.39×106次,大约能使用887 h。从图9b 中可以看出,环模在模辊最小间隙处疲劳破坏呈“H”形分布,即在模孔处和靠近两壁面处疲劳寿命开始降低。这是由于物料不断被压辊挤入进环模模孔中,在环模模孔处附近容易造成应力集中的现象,导致模孔处容易发生疲劳破坏;在环模两壁面附近的物料无法被挤压进模孔,导致此处应力过大,对环模壁面以及压辊壁面造成疲劳破坏,环模最小寿命3.12×106次,大约能使用439 h。通过对压辊和环模疲劳寿命分析比较可以看出,环模相比压辊更容易发生疲劳破坏。
通过传统方法在模孔内壁施加轴向及周向平均压力载荷来模拟物料对模孔所产生的压力,同时在环模内壁面施加正压力,模拟物料对环模壁面产生的压力,从而得出环模有效受力以及疲劳寿命。将流固耦合所得到的环模疲劳寿命与直接施加载荷,即无耦合状态下的环模疲劳寿命进行对比,得到A 点到B 点的疲劳寿命曲线图,如图10b 所示。
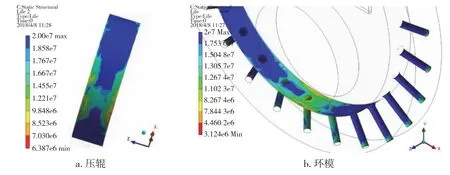
图9 疲劳寿命云图Fig.9 Fatigue life cloud diagram
有耦合状态时,从图10 中可以看出,从A 点到环模模孔入料侧附近所求得的疲劳寿命低于无耦合状态下的疲劳寿命,这是由于耦合状态下环模模孔倒角处附近环模所受应力更集中;而从模孔到B 点处所求得的疲劳寿命高于无耦合状态下的疲劳寿命,这是由于物料大部分被挤压进模孔中,此处物料对环模产生的应力迅速减小,使得环模所受应力减小,疲劳寿命增大,而无耦合情况由于其所采用的是施加平均应力,使得模孔处到B 点疲劳寿命曲线变化平缓。通过分析对比得到流固耦合状态下环模疲劳寿命云图与实际环模疲劳磨损情况吻合[14-15],验证了通过流固耦合来进行疲劳分析方法的可行性。
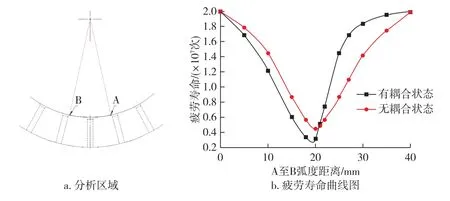
图10 有无耦合情况下环模寿命对比Fig.10 Comparison of ring mold life with or without coupling
4 结论
应用Workbench 建立环模和压辊的单向流固耦合模型,通过映射物料成型过程中物料流体域的压力对环模和压辊的固体域进行应力分析,验证了该仿真模型的有效性,并得到了环模和压辊在成型过程中的受力情况以及变形量。通过Fe⁃Safe 软件建立20CrMnTi 材料的S⁃N曲线,并求得环模和压辊的疲劳寿命。通过对环模和压辊疲劳特性进行分析可以得出在物料制粒成型的过程中,环模和压辊容易发生疲劳破坏的区域,以及在生产过程中,环模较压辊相比更容易发生疲劳破坏,从而可为改进环模与压辊提供理论支持。通过对有无耦合状态下环模疲劳寿命进行对比,得出通过耦合求得的环模寿命符合环模成型机实际磨损的结果,验证了通过流固耦合来分析环模压辊寿命的可行性和准确性。
