CAPM模型在中国沪深股票市场中的实证研究

何小蓉，胡日东

(华侨大学 经济与金融学院,福建 泉州，362021)

资本资产定价理论在金融工程学中有着十分重要的地位，是金融投资学的重要支柱。20世纪50年代，Markowitz发表了论文《资产选择：投资的有效分散化》，首次提出了收益率的风险是由收益率方差来衡量的，建立了里程碑式的均值-方差资产组合模型。20世纪60年代，William Sharpe、Jone Lintner和Mossin在资产组合理论的基础上，结合市场证券组合原理、两基金分离定理和市场均衡原理，提出了著名的资本资产定价模型(CAPM)。CAPM模型已经适用于一些西方发达国家的资本市场，是个人投资者、投资机构进行证券投资操作、资本资产定价的重要工具之一。

近年来，在中国改革开放的背景下，经济发展迅速，中国上海、深圳股票市场不断扩大，资本市场制度不断规范化。中国股票市场表现出与西方发达国家不同的特点，例如中国上海股票市场实行的交易制度是“T+1”，但是西方发达国家的股票市场上一般实行的是“T+0”。上海、深圳证券交易所经由多年的快速发展，市场结构较为完整，已拥有债券、基金、股票、衍生品四大类证券交易品种。CAPM模型理论不仅有助于投资者衡量股票价值，也为个别资产提供了可以量化的风险测度，它对金融资产定价、投资者决策起着重要的指导意义，因此有必要对CAPM模型在我国沪深股市的应用进行研究。

一、文献综述

关于CAPM模型在现实资本市场适用性的争议一直存在，国内外学者运用不同的方法对此做过研究。Jensen[1]等以纽约交易所在1926-1965年期间的股票数据，验证了风险系数值β与股票期望收益率的关系是呈正相关的，与零β资本资产定价模型一致；Fama和MacBeth[2]使用1969年以前的股票数据通过横截面线性回归方法，增加了非系统风险因素和β2，检验了系统性风险β是否是影响资产预期收益率的唯一因素，结果表明风险系数β和所有股票的平均收益呈正相关关系；Roll批判了CAPM模型的有效性，因为无法在实践中证明有效的市场组合就是市场指数组合，而市场组合在CAPM模型中要求其包含的所有资产应是风险性资产；Banz提出股票收益具有“规模效应”；French和Fama[3]在CAPM模型检验中加入财务杠杆、规模、E/P和BE/ME的测试，发现β值的解释能力很弱。随后更多学者从一开始的单因素检验转变为多因素检验，并逐渐成为当前检验资本市场中CAPM模型适用性的主流方式。

CAPM模型是检验资产收益与风险的核心理论，我国学者对其进行了实证检验。施东晖[4]研究了该模型在中国的适用性，得出股票风险与收益之间的正线性相关关系不成立，系统风险并不是影响资本资产定价行为的唯一因素；阮涛和林少宫[5]以上海股票市场1996-1998年间股票收益数据为研究对象，通过横截面分析得出CAPM模型不适合在上海股票市场中运用；许涤龙和张钰[6]以上海股票市场2000-2002年间的部分股票数据为研究对象，采用双层回归检验法，结果表明沪市风险系数值β与股票收益率呈正相关，但是无风险收益率为负，意味着上海股票市场投资者表现出的投机性较高，市场机制还需进一步完善；朱顺泉[7]用2003-2006年间沪市的股票收益数据检验出沪市股票的系统风险与所选取的股票的平均超额收益率的正向关系是存在的；翟羽[8]在市场股权分置改革背景下，以2013-2014年间的股票数据进行实证研究，发现在中国股票市场中，CAPM模型的适用性较好；王丹彤[9]运用2013年到2018年的沪深股票市场80支股票数据检验得出，沪深A股市场更加适合风险偏好投资者，CAPM模型并不能完全适用于中国股市。

回顾国内外文献可知，由于CAPM模型严格的基本假设条件，大多数研究表明CAPM模型不适用于我国的股票市场，此外，诸多研究所选的股票数量较少，时间跨度较小，造成研究结果不一致。随着证券市场不断发展，我国行情发生了很大的变化，因此进一步研究CAPM模型在我国的适用性十分必要。2008年中国股市深受股灾的影响，股价波动异常，因此这个时间段的股票数据对于本文研究不具有较大意义。鉴于此，选取沪深股票市场2009-2019年间的股票收益数据，采用传统的BJS和FM方法检验CAPM模型在该市场中的适用性。

二、CAPM理论概述

资本市场中有两种风险，一种是系统风险，这种风险是指由国家政策、经济、社会环境等因素造成股价波动，且不能通过投资资产组合来消除的风险；另一种是非系统风险，一般是企业内部的或某个行业中特定存在的，并且可以通过其他手段消除的风险。CAPM模型的主要特点是：(1)只有系统性风险是唯一影响股票收益的因素，在债券定价中起重要作用。(2)如果投资风险确定，投资者倾向于预期收益率相对较高的资产；如果投资回报确定，投资者会投资风险最小的资产。

(一)CAPM模型基础假设

CAPM模型是以若干理想化的假设条件建立的，其基础性假设有：(1)投资者都是风险回避者，其投资行为的终极目标是使其财富期望效用最大化；(2)资产收益率的概率分布是联合正态分布，这是市场中所有资产共同服从的分布；(3)资本市场中存在无风险收益率，投资者可以向银行以无风险利率借入或贷出不限量的无风险资产，即投资者的信用额度是无限的；(4)资本市场的资产数量是固定的，而且所有资产都可以任意组合、自由交易；(5)投资者只能接受市场中的价格，即投资者的行为选择不会影响股票市场上资产的价格波动；(6)市场是完全信息市场并且资本市场是没有摩擦的，无卖空限制、无税收、无交易成本等。

(二)CAPM理论模型

Sharpe-Lintner模型假定投资者能够以无风险利率进行借贷[10]，CAPM的期望形式可表示为：

E(Ri)-Rf=βi[E(RM)-Rf]

(1)

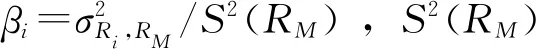
三、CAPM模型的实证研究

(一)指标选取

为更全面地研究中国沪深股票市场，在选择样本时间区间时剔除了不连续的股票，最终选取沪深300指数的193支成分股作为研究对象，占总比约2/3。综合国内外实证研究，大多采用2～5年的样本期间数据来估计β值，为避免受2008年金融危机的影响，又考虑到沪深300指数的成分股会变动，本文选取的成分股以2019年6月17日变动后的为准，样本区间为2009年1月9日-2019年9月30日共129个月的数据。所有样本股的权重占比为76.55%，涵盖了金融、公用事业、基础化工、有色金属、餐饮旅游、医药生物、电气设备等20多种行业，具有鲜明的代表性。

沪深300指数涵盖了沪深两个A股市场，客观真实地反映了A股市场上的运行状况，并且其剔除了ST、*ST等劣质股，样本股都是规模大、流动性好的优质股，可以较为全面地反映中国股票市场价格变动趋势与市场投资变动情况，其指数的编制方法更优，采用派许加权综合价格指数公式进行计算，这和CAPM模型所要求的市场组合相似，因此本文的市场指数选择沪深300指数。

无风险利率是指投资者向金融机构在没有风险的条件下借入资金的利率。综合比较国内外研究，一般采用短期国债利率或银行同业拆借利率代替无风险利率，本文采用一年期国债收益率代表无风险收益率。

沪深300指数的周收益率Rt的计算公式为：

Rt=(Pt-Pt-1)/Pt-1

(2)

其中Rt是市场组合在第i周的收盘价，Pt-1是市场组合在第i-1周的收盘价。个股股票周收益率数据来源于锐思金融研究数据库。

(二)研究方法和实证分析

本文运用传统的BJS和FM方法相结合的双层回归检验法，主要利用R进行操作检验。BJS方法是由Black、Jensen和Scholes主要针对用时间序列方法检验CAPM模型所提出的；FM方法是由Fama与MacBeth在1973年提出的检验CAPM模型的横截面方法。

根据时间顺序将样本股数据分为三组，第一组数据时间区间为2009年1月9日到2012年7月27日，第二组为2012年8月3日到2016年2月26日，第三组为2016年3月4日到2019年9月30日，每组时间区间数据为跨度43个月的周收益率。

1.单支股票β系数的计算

运用沪深股票市场第一组样本数据，采用模型(3)做时间序列检验，从而估算出单支股票的风险值β，最小二乘法回归方程：

Rit-Rf=αi+βi×(Rmt-Rf)+εi

(3)

其中，在第t周时，Rit表示股票收益率，Rmt为市场指数的收益率，Rf为无风险利率，εi为随机误差项，αi和βi为待估计参数。模型检验回归部分结果见表1。

表1 单支股票最小二乘回归方程部分结果Tab.1 Partial results of least square regression equation for single stock

2.市场组合βp系数的估计

将股票数据按照在第一组样本期间估算的风险系数值由小到大排序，然后按照大小顺序分组，每19支股票等权重地组成10个证券组合。第一个股票组合有22只股票，后9个股票组合每组19支股票，运用第二组时间区间的数据，股票组合的周收益率可以通过简单算术平均法来计算得出：

Rpit=(1/N)∑Rit

(4)

其中，第t周时，第i个证券组合的收益率是Rpit，此组合中第i支股票的收益率是Rit，这个组合中所含有的股票数量是N。

将沪深300的周超额收益率作为自变量，将股票组合的周超额收益率作为因变量做回归分析，通过模型(5)估算出各个组合的系数βp：

Rpt-Rf=αp+βp×(Rmt-Rf)+εpt

(5)

同时估算出回归残差εpt的标准差σp，各股票组合的系数βp估算结果见表2。

表2 股票组合的最小二乘回归方程结果Tab.2 The results of least square regression equation of stock portfolio

3.资产的收益与风险之间的关系检验

根据第三组时间区间股票数据的周收益率计算出的10个股票组合的平均周收益率，然后运用模型(6)进行线性关系检验：

Rp=γ0+γ1βp+εp

(6)

其中，Rp为每个股票组合在第三组时间区间的平均周收益率，βp是运用第二组样本股票数据估计的风险系数值，γ0、γ1为待估计参数。

4.横截面检验

上述时间序列检验的效果不理想，因此下文将已求得的股票组合的βp系数作为系统风险，将其残差的标准差作为非系统风险，进行二次回归检验，二次回归方程FM模型为：

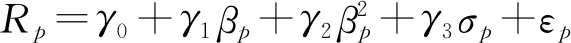
(7)

其中，Rp是股票组合的周平均收益率，βp是股票组合的风险系数值，σp是在最小二乘回归方程中估计残差的标准差，可看作是非系统风险成分，γ0、γ1、γ2、γ3是待估计参数。

该二次回归方程将进一步检验股票价格的唯一影响因素是否为系统性风险、股票收益与其风险之间的关系是否为正线性关系。而对CAPM模型进行横截面检验，最重要的是验证以下几个假设：(1)假如预期结果与CAPM模型一样，那么检验结果中γ2=0；(2)股票组合的风险是由系统风险系数值βp所衡量的，非系统风险不影响股票定价，投资者如果承担非系统性风险也得不到补偿，那么在回归方程中检验的系数γ3=0；(3)证券市场中投资者是讨厌风险的，并且认为高风险必定会带来高收益，即资产的期望收益与其承担的系统性风险呈正相关关系，那么γ1≥0，且γ1=E(RM)-Rf；(4)γ0=Rf。

图1 贝塔数值箱线图Fig.1 Beta value box plot

四、结果与分析

(一)单支股票的β估计值分析

在进行时间序列检验的193支股票中，有124支股票在上海证券交易所上市，69支在深圳证券交易所上市，包括了农业、牧业、渔业、林业、热力业、电力业、制造业、采掘业及综合行业等多个行业，能较为全面地反映整个证券市场的行情。根据每支股票的最小二乘回归结果，单支股票风险系数值β统计图显示(见图1)，每支股票的β值中位数是0.93，50%的值都落在了0.74和1.1之间；最小值为0.29，最大值为1.54，有两个异常值0.000 6和1.686 0，两者相差较大；有39.9%的样本股票的β值大于1，有6支股票的β值等于1，有56.99%的股票β值小于1，总体样本股票β均值为0.92。39.9%的样本股票β值大于1，说明市场的收益率高于股票的收益率，即投资者在证券市场中并不都是风险回避者；但是有近60.1%的股票β值小于等于1，说明较于之前的研究，投机者减少，目前股票市场中的股票风险大多小于市场风险，比较符合CAPM模型的基本假设。为表明市场组合变动超额收益1%对于单支股票周超额收益变动的影响，根据估算结果统计有76.68%的样本股R2值小于0.5，表明模型拟合优度欠佳。

(二)股票组合的βp估计值分析

在10个股票组合中，风险系数βp的最大值为1.18，最小值为0.75，总体均值为0.95(见图2)。有7组股票组合βp<1，有3组股票组合βp>1，通过对比单支股票的风险系数值，说明投资股票组合的方式可有效分散风险，市场中仍然存在非系统性风险，并影响股票收益。由检验结果可知，模型βp值通过显著性检验，并且模型中α值在不同水平上均显著，通过了F检验。股票组合R2值均值为0.82，最小值为0.72，最大值为0.9，该模型具有较高的拟合优度。

图2 股票组合贝塔值统计图Fig.2 Statistical chart of beta value of stock portfolio

(三)风险与股票收益线性关系分析

将股票组合的风险系数βp值作为自变量，将股票组合收益率作为因变量，作散点图(见图3)。股票组合的βp值与收益率的线性关系较为明显，但是仍有高收益的股票组合承担了较低的风险，高风险的股票组合收益率却相对较低，说明市场机制尚不成熟，仍有投机者参与其中。

图3 股票组合收益率与贝塔值关系散点图Fig.3 Scatter chart of the relationship between the return of stock portfolio and beta value

采用最小二乘回归模型对股票组合周收益与其承担的系统风险之间的关系进行检验，得出的回归结果见表3。可知：(1)γ0=0.007 516>0，说明无风险利率大于0，这与现实情况是相符的，表明在资本市场中，存在无风险资产；(2)γ1=-0.005 271<0，说明股票组合的收益率与其承担的风险之间呈反比，这与现实情况相悖；(3)R2=0.625 6，说明该模型的拟合优度较好，且βp通过了显著性检验。

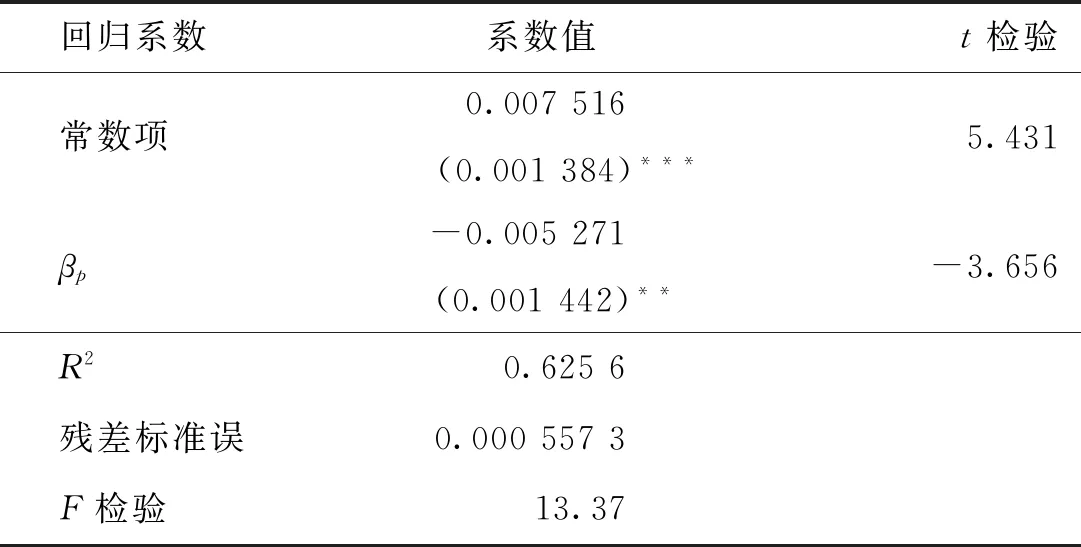
表3 股票组合最小二乘回归结果Tab.3 Least squares regression results of stock portfolio

(四)横截面检验结果分析

在横截面检验中，运用一元二次回归模型对股票组合周收益和风险进行检验，加入非系统性风险因素σp以及β2作为自变量,检验结果见表4。可知：(1)γ1=-0.000 3<0，说明股票组合承担的风险与收益率之间不呈正线性关系，市场中存在投机者并且γ1≠E(RM-Rf)，γ2=0.002 6>0，但是影响因子非常小，基本符合CAPM理论；(2)γ3=0.036 0≠0，说明影响证券市场中资产定价行为的因素包括非系统风险，这与CAPM模型中的基本假设不相符；(3)γ0=0.046 2>0，说明在资本市场中，无风险资本收益率为正数，这与现实情况基本相符；(4)模型中R2=0.65，模型拟合优度较好。

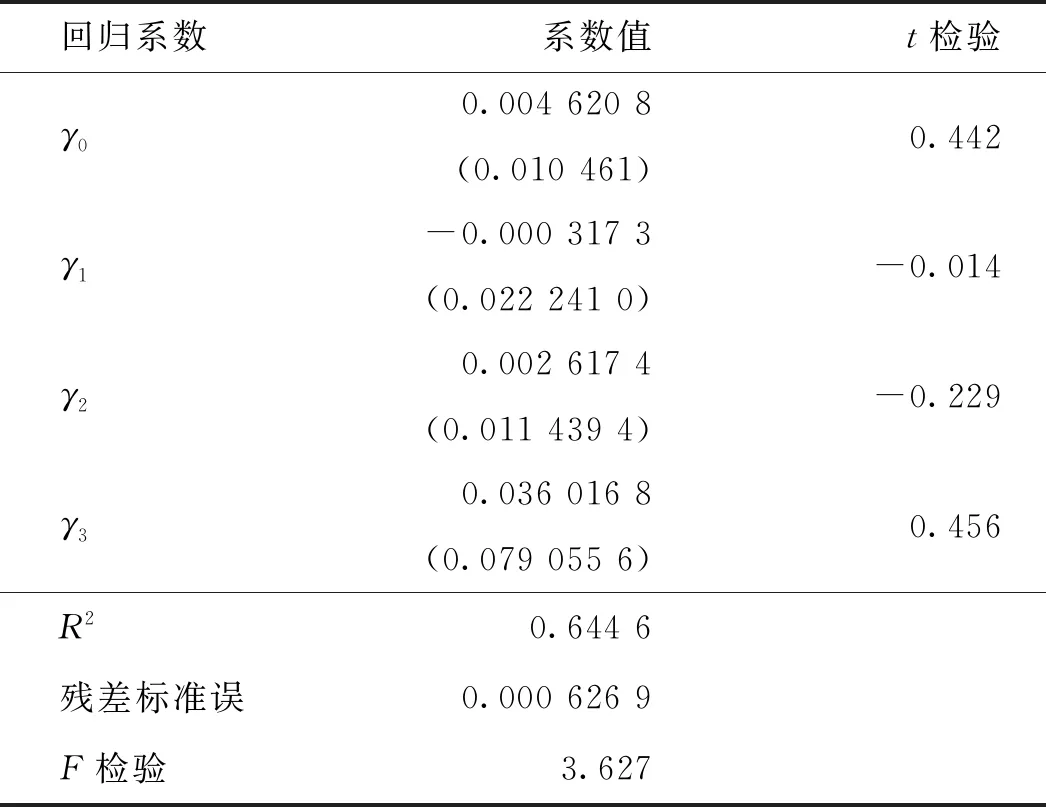
表4 二次回归方程结果Tab.4 Results of quadratic regression equation

五、结论与启示

CAPM模型是金融市场上一个重要的金融资产定价模型，具有可操作性和简单性的特点，在资产定价、证券收益预测、投资风险分析中有着重要的作用[11]。但是CAPM模型理论是以许多严格的基本假设为基础的，而中国沪深股票市场相对于西方国家发展较慢，是一个不完全成熟的市场。随着时代发展，人们意识到防范风险的重要性，而通过投资股票组合可有效分散风险，相对于单支股票而言，股票组合更能达到CAPM理论要求，拟合优度较高。高风险伴随着高收益，但是无法完全满足CAPM模型理论的基本假设。目前CAPM模型在我国沪深股票市场中有弱适应性，CAPM模型的系统风险测度更能解释股票组合的收益率。在沪深股票市场中，虽然系统风险发挥着重要作用，但非系统性风险也能在资产定价中起到一定的作用，系统风险并不是引起股票收益率变动的唯一因素。

本文提出以下建议：应在我国沪深股票市场中适当运用CAPM模型，不可过度依赖，同时要考虑非系统性风险对股票价格的影响；应重视系统性风险，进一步完善金融监管体系，逐步增强市场有效性，防范风险发生；应提高证券市场化水平，提高金融市场投资者的金融素养，减少投机者一味追逐利益而加重“高风险，低收益”的现象；加快构建现代金融体系，维护金融市场稳定发展。我国是发展迅速的新兴市场国家，随着市场化程度不断提高，相信在今后金融资产定价理论会更加适应我国沪深市场。