特殊框架下分数(k， m)-一致图的联结数条件研究

高 炜

(云南师范大学 信息学院， 云南 昆明 650500)

在计算机传输网络中， 由于受单个通道容量的限制而无法传输大数据包. 因此， 一般需要将数据进行切割， 分成若干个小块再由各个通道分别传输， 最后在目的地节点进行数据的重新组装. 然而， 在理论上对网络数据传输问题进行数学建模， 用顶点代表节点， 用边代表两个节点之间有直接的数据传输通道相连. 由此， 整个传输网络用一个图来表示， 而数据传输问题则等价为图上的分数流问题. 于是就可用分数因子的存在性来间接刻画网络中数据传输的可行性. 有关这方面的研究成果可参阅文献[1—4].

而由于本文只考虑有限无环无重边的无向图， 也就是说，假设两节点之间数据传输是双向的. 设G=(V(G)，E(G))是一个图， 其中V(G)和E(G)分别为顶点集和边集. 对任意顶点子集S， 设G[S]是S的导出子图，dS(x)和NS(x)分别表示顶点x在G[S]中的度和邻域集. 设δ(G)=min{d(x)：x∈V(G)}为图G的最小图. 对于G的不相交子集S，T， 设eG(S，T)为一端在S， 而另一端在T的边的数量. 设H为边集合，eH(S，T)表示一端在S， 另一端在T， 且属于集合H的边的数量. 并设n=|V(G)|表示图的阶.

特别地， 在上述定义中取m=1， 则分数(k，m)-消去图、 分数(k，m)-覆盖图和分数(k，m)-一致图分别为分数k-消去图、 分数k-覆盖图和分数k-一致图.

而联结数是图网络的重要指标， 用于衡量网络的稳定性和易受攻击程度.

本文的主要目的是研究联结数和分数k-因子存在性的联系， 我们将分别给出分数(k，m)-覆盖图的联结数条件， 进而得到分数(k，m)-一致图的条件.

1 主要结果

本文的主要结论陈述如下.

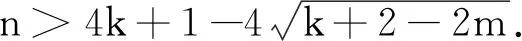
定理1和定理2的证明主要通过以下引理的证明来完成.

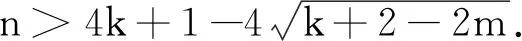
而引理1和引理2的证明需要如下已知结果的支持.

引理3设k≥1，m≥0为两个整数. 设G是一个图. 则G是分数(k，m)-覆盖图当且仅当对任意含有m条边的子图H和任意S⊆V(G)有

(1)

其中T={x：x∈V(G)-S，dG-S(x)≤k-1}.

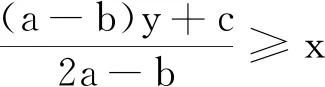
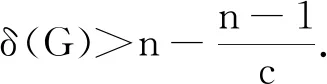
2 定理1和定理2的证明

其中T={x：x∈V(G)-S，dG-S(x)≤k-1}. 显然有T≠φ.

设dmin=min{dG-S(x)：x∈T}， 则有dmin≤k-1. 利用引理4和引理5， 并且重复文献[5]中对分数(k，m)-消去图的证明过程， 便可得到引理1和引理2. 同时， 利用文献[5]中给出的一些反例， 也可以说明引理1和引理2中对分数(k，m)-覆盖图的联结数条件是紧的.

最后， 把引理1和引理2与文献[5]中的关于分数(k，m)-消去图的两个结论(该文中的定理5和定理6)相结合， 即可得到定理1和定理2. 同时， 文献[5]的一些反例同样可以说明定理1和定理2中对分数(k，m)-一致图的联结数条件也是紧的.

3 讨论

本文研究发现， 文献[5]中关于分数消去图的证明过程， 可以完全用于引理1和引理2中关于分数(k，m)-覆盖图的联结数条件的证明. 这让我们自然发出一个疑问：是否所有关于分数(k，m)-消去图的结果都可以套用到分数(k，m)-覆盖图， 进而得到分数(k，m)-一致图的结论？这个问题的答案是否定的.

要解答这个问题， 我们需要从分数(k，m)-消去图和分数(k，m)-覆盖图的充要条件入手. 设k≥1，m≥0为两个整数. 设G是一个图. 则G是分数(k，m)-消去图当且仅当对任意含有m条边的子图H和任意S⊆V(G)有：

(2)

其中T={x：x∈V(G)-S，dG-S(x)-dH(x)+eH(x，S)≤k}(可以直接验证这里的集合T可以修改为T={x：x∈V(G)-S，dG-S(x)-dH(x)+eH(x，S)≤k-1}). 然而， 在处理大部分分数(k，m)-消去图相关问题时， 我们倾向于使用另外一种形式的充分必要条件：G是分数(k，m)-消去图当且仅当对任意含有m条边的子图H和任意不交子集S，T⊆V(G)有：

也就是说， 任意S和T={x：x∈V(G)-S，dG-S(x)≤k}， 与任意不相交的S，T⊆V(G)是等价的. 显然， 若对任意不相交的S，T⊆V(G)， (2)式成立， 则对于任意S和T={x：x∈V(G)-S，dG-S(x)≤k}， 不等式(2)也能成立.

反之， 假设对于任意S和T={x：x∈V(G)-S，dG-S(x)≤k}， (2)式成立. 那么对于任意的不相交子集S，T⊆V(G)， 把T分成两个部分：

T1={x∈V(G)-S|dG-S(x)-dH(x)+eH(x，S)≤k}；

T2={x∈V(G)-S|dG-S(x)-dH(x)+eH(x，S)>k}.

对于第1部分T1， 根据假设条件可得：

(3)

对于第2部分T2， 由它的定义得：

(4)

于是， 立刻可以用(3)式和(4)式， 验证(3)式+(4)式=(2)式， 由此可知关于分数(k，m)-消去图， 可以验证不同的充要条件之间的等价性.

T1={x∈V(G)-S|dG-S(x)≤k-1}；

T2={x∈V(G)-S|dG-S(x)≥k}.

对于第1部分T1， 根据假设条件可得：

(5)

对于第2部分T2， 由它的定义得：

(6)

通过(5)式+(6)式和(1)式对比， 发现缺少eH(S，T2)项. 由此可知， 关于分数(k，m)-覆盖图的充要条件中的任意S和T={x：x∈V(G)-S，dG-S(x)≤k-1}不能改为任意的不相交子集S，T⊆V(G).

事实上， 大部分关于覆盖图的情况需要重新考虑， 并不能把消去图的证明过程照搬. 本文的结论只是凑巧， 原来的证明过程可以直接拿来用. 由于定理1和定理2的结论只对小m才能满足， 即被条件k+1≥2m或k+2≥2m所限制， 因此， 给出如下的开问题作为本文的结束.

开问题对于一般的m， 需要什么样的联结数条件才能保证G是分数(k，m)-覆盖图和分数(k，m)-一致图？