基于one-fluid模型的波浪-浮体相互作用数值模拟研究

田昀艳，王收军，陈松贵，王家伟，胡原野

(1.天津理工大学 机电工程国家级实验教学示范中心，天津 300384；2.交通运输部天津水运工程科学研究所，天津 300456)

在波浪与结构相互作用的研究中，通常采用物理模型实验和数值模拟相结合的方法。近年来，随着高性能计算机技术的发展和数值离散方法的成熟，构建数值波浪水槽并研究水波与结构物的相互作用问题，已成为海岸和海洋工程领域不可缺少的研究方法。

在波浪力学领域，波浪与结构相互作用的建模一直是通过基于势流理论和粘性流理论的数值波浪水槽方法发展起来的。由于势流理论是建立在不可压缩和无粘流动假设的基础上的，该方法不能模拟粘性效应和破碎波。因此，在实际工程应用中，Navier-Stokes方程被用于模拟波浪与结构物相互作用问题。Park J.C.和Uno Y[1]等人，在粘性三维数值波浪水槽中模拟了规则波、不规则波以及多向随机波，并讨论了在特定波浪作用条件下船舶的水动力特性；Hans Bihs[2]等人采用Level Set法追踪自由表面，建造三维粘性数值波浪水槽，对波浪在倾斜海滩上传播及破碎过程、垂直圆柱上的波浪力、孤立波与矩形桥台之间的相互作用进行了模拟；孙宏月等[3]基于紧致差值曲线方法建立了可压缩两相流数值波浪水槽模型，模拟了波浪对结构物的冲击过程；余阳等[4]基于OpenFOAM平台，采用重叠网格技术建立了黏性数值波浪水池，验证了重叠网格在二维和三维两相流体区域中流体与结构相互作用的准确性和可靠性；张弈泽等[5]采用Flow3D软件建立数学模型对越浪量进行了模拟研究，对防浪墙顶高程的合理性进行分析，并对不同形式的海堤护面结构进行数值模拟研究；焦方骞等[6]基于OpenFOAM软件建立了波浪与结构物相互作用的三维数值波浪水槽，模拟了复合筒型基础在不同波浪条件下的波浪载荷；Patankar[7]以欧拉方式将刚体看作流体，通过两相流方法对刚体和流体耦合建模问题进行简化，刚体的惯性完全由流体求解器承担，但是施加的刚性力是在离散水平上进行的。上述基于NS方程对波浪与结构相互作用的研究大多是基于两相流的水平集函数，不能用于解决浸没结构多相多界面问题的演化。与上述大多数可用的浸入边界方法不同，Yang[8]提出了一种模拟非线性粘性波浪产生全物理过程的one-fluid模型。通过提出一种基于线性最小二乘法求解刚体的运动约束，在连续介质水平上明确表达了浸没刚体的力,不需要诸如质心、质量和惯性动量之类的信息，只需要知道刚体的密度。这种方法将刚体与流体耦合问题重新表述为一个带有附加刚体运动约束的三相浸入流动问题。该模型可以用于处理大密度比、多相流问题，已成功应用于水下刚性板的颤振运动[9]以及波能转换器(WEC)的数值研究[10]等。

鉴于以上背景，本文基于one-fluid方程建立了二维粘性数值波浪水槽，进行了不规则波的模拟并且研究了浮式结构在不规则波作用下的动力响应。第一节介绍了one-fluid方程的数值求解过程以及自由表面的处理方法等；第二节对不规则波进行了数值模拟，并研究了不规则波与浮式结构之间的相互作用；第三节探讨了不规则波作用，波高、周期、浮体宽度与波长的相对宽度以及浮体的相对吃水对浮式结构物的垂荡运动响应的影响；第四节给出了相关的结论。

1 数学模型

图1 流体与刚体相互作用问题的拉格朗日力学耦合与one-fluid框架的说明

1.1 控制方程

在one-fluid模型中，一个方程里同时考虑了多个不可压缩相，包括空气、水和结构。与其它刚体-流体耦合问题处理方法不同之处在于它利用线性最小二乘法，提出了一种用于刚体运动约束的刚体投影算子。该算子在连续介质水平上明确地表达了浸没刚体的力，不需要诸如质心、质量和惯性动量之类的信息。该模型可以用于处理大密度比、多相流问题。传统模型中，耦合力是通过转矩tc和外力fc来实现的，而在one-fluid模型中，耦合是通过界面上的平衡牵引矢量来实现的。图1说明了流体与刚体相互作用问题传统解决方法和one-fluid模型之间的差异。

one-fluid模型中，一个方程中同时考虑了多个不可压缩相，包括空气、水和结构。在整个区域Ω=Ωa∪Ωw∪Ωr(在没有表面张力的情况下)三相系统的线性动量守恒方程和连续性方程用一个方程表示如下

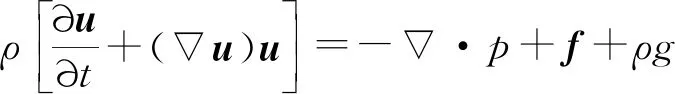
(1)

式中：u是速度矢量(u，v)，ρ=ρrHr+ρwHw+ρaHa，其中下标a、w、r分别表示空气、水和刚体的相，H是不同相的Heaviside分布。式(1)中的体积力f定义在每个相位上表示如下

(2)

其中应变率张量D(u)=(u+(u)T)/2，μ表示动力粘度系数。P(u)是刚性速度投影算子。

1.2 自由液面捕捉

one-fluid模型的表述依赖于连续体不同相之间界面的正确识别，可以通过在界面上引入合适的跳转条件进行。在采用浸没边界方法的情况下，可以通过界面的平滑正则化避免明确使用跳转条件。水、空气和结构这三个不同的区域由三个Heaviside函数表示。通过三个Heaviside函数来描述界面的具体步骤如下：

忽略刚体，与两相流问题类似，引入了水平集函数来识别空气和水之间的界面。带符号的距离函数φ给出了最接近界面的距离Γ，并且通过符号的变化来区分这两个相位，因此满足下式

Γ={x∈R2|φ(x,t)=0}

(3)

(4)

式中：phase1表示水；Γ表示自由液面；phase2表示空气。当界面Γ在外部生成的速度场u下移动时，将获得水平集函数的对流方程如下

(5)

①引入刚性Heaviside函数Hr(x,t)=Hr(X,0)来识别刚体区域。其中：X表示拉格朗日坐标；欧拉坐标x=Ψ(X，t)；Ψ表示从X到x的映射；

②“刚体”、“水”、“空气”所占据的区域定义如下

Ωrigid={x∈R2|Hr(x,t)=1}
Ωwater={x∈R2|Hφ(x,t)-Hr(x,t)=1}

(6)

Ωair={x∈R2|1-Hφ(x,t)-Hr(x,t)=1}

使用两个Heaviside函数表示三相的图示如图2所示。

图2 使用两个Heaviside函数表示三相的图示

1.3 Heaviside函数的求解

①平滑流体Heaviside函数：

Heaviside函数的演化遵循Ha(x,t)=H(φ(x,t))，其近似值可以表示如下

(7)

其中∈代表拖尾带宽的参数。因此，在涂抹界面上，Heaviside函数的近似值从零变为一，从而描述了从一个相到另一个相的平滑过渡。

②平滑刚体Heaviside函数：

在初始时间t=0时，引入卷积程序来规定任意的Heaviside函数。

步骤1：给定笛卡尔网格，将值1赋给描述刚体的多边形，该多边形是非光滑离散的Heaviside函数Hr。

步骤3：将非平滑的Heaviside函数与光滑的Dirac Delta函数卷积得到平滑的Heaviside函数

(8)

图3 边界和松弛区示意图

1.4 边界条件

多相流数值水槽模型采用速度边界入口法和松弛消波法来实现造波和消波功能，边界和松弛区如图3所示。模型左侧为速度入口边界条件，通过自定义函数给定入口边界的速度和波面变化；计算域底部为滑移壁面边界条件；水槽右端为封闭边界条件。图中松弛区Ⅰ的功能是协助波浪的产生以及吸收从结构物反射回来的波浪；松弛区Ⅱ的功能是消除出口边界的反射波。波浪在造波区和消波区的速度、波面以及压力的计算公式见文献[11],不规则波水质点的波面方程、垂直速度与水平速度方程见文献[12]。

1.5 多相流求解器求解过程

(1)通过卷积初始化流体速度u0、水平集方程φ和Heaviside函数H。

(2)开始非定常计算的时间步循环。

1)在不考虑粘性的情况下，通过one-fluid动量方程来计算中间速度场u*，ρ(u*-un/Δt)=RHSn，其中RHSn=-ρ(un)un+ρg，上标n表示时间步长。

2)计算区域Ωr的刚性力fn：

①线性最小二乘法：通过最小化‖P(u*)-u*‖2来找到刚性速度场P(u*)；

②将刚体力更新为：fn=ρ[p(u*)-un/Δt]-RHSn。

3)计算粘性项：fn=μ·2μD(un)。

4)考虑粘性，通过one-fluid动量方程来计算中间速度场u**：ρ(u**-un/Δt)=RHSn+fn。

5)用Neumann边界条件计算压力以满足不可压缩约束条件：·(pn/ρ)=-·u**/Δt。

6)应用速度校正：un+1=u**-Δt·pn/ρ。

7)计算水平集对流方程并重新初始化。

8)基于高阶插值的刚性Heaviside函数对流化。

9)更新下一时间步的速度un+1和密度ρn+1。

2 数值水槽模型验证

为了验证数值水槽模型的有效性，本文对不规则波进行了模拟，并研究了浮式结构在不规则波作用下的动力响应。

表1 不规则波模拟目标参数

2.1 不规则波浪的数值模拟

为了验证one-fluid模型的准确性，应用合田改进后的JONSWAP谱对在交通运输部天津水运工程科学研究所大比尺波浪水槽实验室实测的不规则波数据进行了分析和数值再现。选择了三组不同工况下浪高仪所记录的波面数据进行比较分析，模拟工况如表1所示。数值波浪水槽计算模型的设置与交通运输部天津水运工程科学研究所的大比尺波浪水槽一致，如图4所示。模型尺寸为450 m×12 m，消波段长60 m。计算网格尺寸为3 800×100，时间步长取0.02 s。在数值水槽距离造波边界150 m处设置虚拟浪高仪G1来监测波面变化。

图4 数值波浪水槽示意图

图5给出了按JONSWAP谱进行模拟得到的x=150 m处的不规则波面时历曲线与实测不规则波面时历曲线。对波浪时历进行统计分析可得有效波高及有效周期的计算值见表2，所得结果与实验值吻合较好。还可以得出one-fluid模型对于波高为Hs=1.55 m和Hs=1.8 m的模拟结果要好于波高为Hs=1 m的，随着波高和周期的增大，数值计算所得结果与实验值的误差越小。

5-a 工况a

表2 计算值和实验值的比较

表3 计算所得波能谱和实验所得波能谱的比较

图6给出了波面经过傅里叶变换之后得到的频谱与目标靶谱的对比图。从图中可以看出，得到的频谱与目标靶谱基本吻合。表3给出了由实验所得的波能谱与one-fluid模型计算所得波能谱的值，可以看出one-fluid模型模拟的谱峰频率与实验所得的谱峰频率两者吻合较好，表明本文模拟的不规则波具有一定的准确性。

6-a 工况a

2.2 预测不规则波与结构物相互作用

为了验证所建立的数学模型预测结构与不规则波相互作用的准确性，本文数值模拟了William等人[13]的案例。利用one-fluid模型的“刚体”流固耦合特性对浮体结构进行了建模。

本验证计算所选取的数值水槽几何尺寸、波浪参数、浮式结构尺寸以及距水槽的初始位置等均参照William等人的数学模型设置。模拟过程中的波面数据来源于大西洋海能测试站点浮标所记录的三个不同时段的数据，时间分别为2010年12月17日10:30、2010年10月10日4:30、2011年2月9日17:00。空气、水和浮式方箱的密度分别取1.0 kg/m3、1 000 kg/m3和750 kg/m3。空气和水的粘度分别为17.9×10-6Pa·s和1.0×10-3Pa·s。本文仅针对结构物的垂荡运动进行研究分析。

图7显示了不规则波与结构物之间在多个时间步长上的相互作用，包括波浪剖面和结构物的动态响应。

7-a t=120 s时

为了评估模型的准确性，将数值波浪水槽的垂荡运动动态响应与结构水动力分析得出的解析解以及William等人数值分析所得到的结果进行了比较，结果如图8所示。可以看出：本文数值模拟得到的结果与William等人数模的结果在频率和幅值方面吻合度都很高。而由one-fluid模型得到的结果与结构物水动力分析得到的结果在频率方面匹配的很好，但两者的响应幅度所得结果有所不同。这是由于数值模型从稳定状态开始，因此在模拟初始部分与水动力计算软件AQWA得到的结果存在很大差异。这种差异可能是由于浮式结构物的位置变化和倾斜情况的影响，从而导致整个运行过程中的润湿面发生变化所造成的。在采用one-fluid耦合模型时，考虑了这一因素对浮体水动力荷载的影响，而由结构水动力分析得到的解析解中忽略了这一影响。此外，结构物本身壁面或波浪水槽的数值模型中存在粘性非线性影响，会导致阻尼力增加，然而AQWA是基于势流理论的水动力计算软件，在计算过程中不考虑流体粘性，结果有一定误差，这可能导致one-fluid模型与解析解之间的差异。

8-a 2010年12月17日10:30

3 数值水槽模型应用

入射波的周期、波高不同，波长也不同，对浮体的受力也不尽相同。结构物在与波浪相互接触时，不仅会受到波浪的冲击载荷，而且由于波浪的形态变化，结构物浮心位置也会随之发生变化，因此结构物在波浪中的运动响应是由多种因素共同作用产生的。

表4 波高、周期的取值

本节探讨了在不规则波作用下，波高、周期、相对宽度(浮箱宽度与波长的比值W/L)以及浮箱相对吃水对浮式方箱垂荡动态响应的影响。二维数值水槽模型长28 m，高1 m，其中水深0.6 m,消波段长5 m。水平方向网格为896个单元，垂向网格为32个单元，时间步长取0.015 s。数值模拟波要素的选取见表4～表6。

表5 相对宽度的取值

表6 浮箱相对吃水的取值

从图9中可以看出，浮体的垂荡值随着波高的增大而增大。在不同的波高下，浮体的垂荡曲线呈现出一定的周期性。当波高Hs=0.07 m时，垂荡峰值0.048 m；当波高Hs=0.08 m时，垂荡的峰值为0.056 m；当波高Hs=0.1 m时，垂荡的峰值为0.075 m。通过对比三种工况可以看出，随着入射波高的增加，浮式方箱垂荡运动响应也增大。

从图10中可以看出，在不同的周期下，浮体的垂荡曲线也呈现出一定的周期性。运动大都在30 s后保持稳定，周期Ts=0.91 s、1.1 s、1.28 s对应的垂荡峰值分别为0.086 m、0.075 4 m、0.06 m。从图中可以观察到，入射波周期Ts=0.91 s的情况下，浮体的垂荡峰值最大，然后随着入射波周期变长，运动响应峰值减小。

从图11中可以看出，浮箱的宽度与波长之比W/L=0.163 9、0.294、0.361 4所对应的垂荡峰值分别为0.078 m、0.058 4 m、0.056 m。可以看出相对宽度W/L=0.163 9时浮体垂荡动态响应最大，垂荡运动响应随着相对宽度的增加逐渐减小。

从图12中可以看出，浮体的吃水深度h=0.1 m、0.12 m、0.14 m时，对应的垂荡的峰值分别为0.117 m、0.095 m、0.082 m。可以看出吃水深度h=0.1 m时浮体垂荡运动响应最大，随着浮体吃水深度的增大，垂荡运动响应峰值减小。

图9 不同波高下,高a=0.18 m,宽b=0.3 m的浮式方箱垂荡运动响应曲线

图10 不同周期下,高a=0.18 m,宽b=0.3 m的浮式方箱垂荡运动响应曲线

图11 不同相对宽度下,高a=0.18 m,宽b=0.3 m的浮箱垂荡运动响应曲线

图12 不同吃水深度下，高a=0.2 m，宽b=0.3 m的浮式方箱垂荡运动响应曲线

4 结论

(1)本文使用one-fluid数学模型建立了二维粘性数值波浪水槽。通过对滤波后的实测波与one-fluid模型输出值在时域和频域的比较，发现它们在频率方面吻合的非常好。

(2)将数值波浪水槽模型得到的结构垂荡运动动力响应与结构水动力分析得到的解析解以及william的数值研究结果进行了比较，结果表明三种结果吻合度较高，特别是在频率方面吻合度很高。

(3)研究了不同波高、周期以及浮式结构物的大小对不规则波作用下结构物垂荡动态响应的影响。结果表明随着波高的增加，浮式方箱垂荡运动响应也增大；随着入射波周期变长，运动响应峰值减小；随着浮体相对宽度和相对吃水增大，垂荡运动响应峰值减小。

(4)与现有方法不同的是，one-fluid模型是从刚体的分布拉格朗日乘子法出发，刚体被建模为流体相，并通过类似于空气和水的广义方程求解，刚体的空间速度是通过线性最小二乘投影来计算的。结果表明，浸入式one-fluid公式是适合于模拟波浪-浮体相互作用问题的，而且不需要明确地引入运动学和动力学边界条件。