分数阶p(x)-Laplace算子方程的多解性
2020-02-21张金国焦红英刘邱云
张金国, 焦红英, 刘邱云
(1.江西师范大学数学与信息科学学院, 江西南昌 330022)
(2.空军工程大学基础部, 陕西西安 710051)
(3.西安交通大学数学与统计学院, 陕西西安 710049)
1 引言
本文主要研究如下的分数阶p(x)-Laplace 算子方程
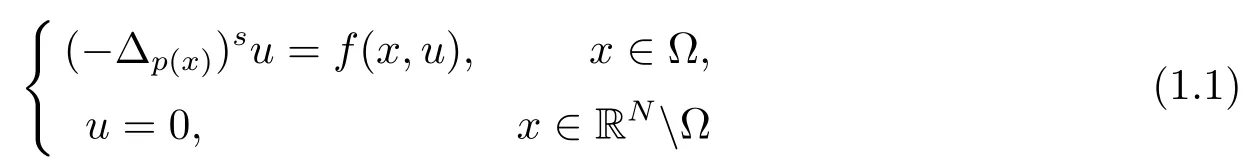
解的存在性问题, 其中Ω 是RN中的光滑有界区域,s ∈(0,1), 连续函数满足sp(x,y) (P2)p是对称的, 即对任意的(x,y)∈有p(x,y)=p(y,x) 成立. (−∆p(x))s称之为分数阶p(x)-Laplace 算子, 其定义如下 这里P.V.表示Cauchy 主值.(−∆p(x))s算子是经典变指数算子∆p(x)的分数阶形式, 该算子的定义在文献[1]中首次给出.关于分数阶变指数算子以及相应的Sobolev 空间理论的研究可参考文献[2–4].从(1.2) 式可以看出(−∆p(x))su(x) 在点x ∈Ω 处的值不仅依赖于u在Ω 上的值, 而且依赖于其在全空间RN上的值.因此, (−∆p(x))s是非局部算子.此外, 问题(1.1) 边界条件是限定在RNΩ 上, 而经典p(x)-Laplace 算子问题的Dirichlet 边界是限制在∂Ω 上.从而经典p(x)-Laplace 算子问题的研究方法是否适合分数阶p(x)-Laplace 算子方程是值得思考的问题.本文试图对这一问题作出解答.有关分数阶Laplace 算子和p(x)-Laplace算子的Dirichlet 边界问题的研究可以参见文献[5–15]. 在本文中, 非线性项f:Ω×R→R 满足如下条件 (f1) 对任意的 (x,t)∈Ω× R, 存在C> 0, 使得 |f(x,t)|≤C(1 +|t|q(x)−1), 其中是分数阶变指数Sobolev 临界指标,s ∈(0,1); (f2)对几乎处处的x ∈Ω 一致成立, 其中 (f3)对几乎处处的x ∈Ω 一致成立; (f4) 存在常数θ> 1, 使得θG(x,t)≥G(x,ηt),∀(x,t)∈Ω× R,η ∈(0,1), 其中G(x,t)=f(x,t)t −p+F(x,t). 注1.1显然上述条件(f4)比(AR)条件更弱,例如函数f(x,t)=p+|t|p+−2tln|t|,∀t ∈R满足上述假设条件, 但不满足(AR) 条件. 定理 1.1设 (P1)–(P2), (f1)–(f4) 成立, 并且对任意的 (x,t)∈Ω × R, 有f(x,−t) =−f(x,t).则方程(1.1) 存在非平凡弱解列并且当n →∞时, 有 Φ(un)→+∞, 其中Φ 是方程(1.1) 所对应的能量泛函. 本文的结构如下:第二节主要是给出变指数Lebesgue 空间和分数阶变指数Sobolev 空间的定义及其相关性质; 第三节给出本文主要结果定理1.1 的证明. 本节主要介绍分数阶变指数Sobolev 空间的一些相关结论.具体证明过程可见文献[5–8, 16, 17]等. 设Ω 是RN中的有界域,记其中 其范数为 由文献[7]可得如下结论. 引理 2.1设u ∈Lq(x)(Ω), 则 引理2.2设u,un ∈Lq(x)(Ω), 则下列结论等价 引理2.3记为q(x) 的共轭指数.设则 称之为变指数Gagliardo 半范.关于空间W有如下嵌入定理. 定理2.2[18]设Ω 是RN中的光滑有界区域,是连续函数使得sp(x,y) 则存在常数C=C(N,s,r)>0 使得从而当时,W连续紧嵌入到空间Lr(x)(Ω) 中. 由于问题(1.1) 的边界条件u= 0 是限制在RNΩ 上, 从而定义如下形式的变指数Sobolev 空间 其中Q=RN×RN(Ωc×Ωc).空间X的范数为其中 注2.2由于Ω×Ω 严格包含于Q中, 所以范数是不同的. 定义X的线性子空间其范数为 对任意的u ∈X0, 定义函数ρX0:X0→R 为 类似于文献[18], 易证得如下结论. 引理2.4对任意的u ∈X0, 有如下结论成立 注2.3(i)是可分、自反、一致凸Banach 空间. (ii) 定理2.2 的结论对空间X0亦成立, 且在空间X0中范数是等价的. 本小节给出定理1.1 的证明. 定义3.1若对任意的ϕ ∈X0, 有下式成立 则称u ∈X0是方程(1.1) 的弱解. 方程(1.1) 相应的能量泛函Φ:X0→R 为 从而泛函Φ 的临界点即为方程(1.1) 的弱解. 引理 3.6(见文献[4, 引理 4.2]) 设函数p满足 (P1) 和 (P2),s ∈(0,1), 对任意的有sp(x,y) 定义 3.2设E为Banach 空间, 泛函I ∈C1(E, R).若满足的序列 {un}⊂E均存在收敛子列, 则称泛函I满足 Ceramic- 条件(简记(C)c- 条件).若对任意的c ∈R,I均满足(C)c- 条件, 则称I满足(C)- 条件. 定理3.3(喷泉定理[19]) 设E为实可分的Banach 空间,E=YZ,其中dimY<+∞.若偶函数I ∈C1(E,R) 满足 (C)- 条件, 且对每一个k=1,2,···, 存在ρk>rk>0, 使得 则泛函I存在一列弱解且I(un)→+∞(n →∞). 下面首先证明泛函I满足(C)- 条件. 引理3.7在定理1.1 的假设下, 泛函Φ 满足(C)- 条件. 证对任意的c ∈R, 设{un} 为泛函 Φ 的(C)c- 序列, 即当n → ∞时, 有 首先证明序列 {un} 在X0中有界.假设{un} 在X0中无界, 即当n →∞时, 有从而存在 {wn} 的子序列, 仍记作 {wn}, 和w0∈X0, 使得 若w0= 0, 取序列 {tn}⊂R 使得对任意的L> 1, 令当n充分大时, 可得 利用条件(f1)和(f3)可得F(x,Lwn)→0(n →∞).从而由L的任意性可得Φ(tnun)→+∞(n →∞).又因为 Φ(0)=0, Φ(un)=c+on(1), 所以当n充分大时有tn ∈(0,1), 从而可得 结合式 (3.2)–(3.4) 和 (f4), 可得 从而当w0=0 时, 序列{un} 在X0中是有界的. 若w00, 则令且 meas(Ω0)> 0.对任意的x ∈Ω0, 有在Ω0中由(f2), 可得 由式(3.5) 和Φ(un)=c+on(1) 可得 从而当w00 时, 序列 {un} 在X0中是有界的.综上所述, 序列 {un} 在X0中有界. 下证该序列{un} 在X0中有收敛子列.因为{un} 在X0中有界, 而X0是自反的, 从而存在{un} 的子列, 仍记作{un}, 以及u0∈X0, 使得unu0弱收敛于X0.由定理2.2 和注2.3, 对任意的q(x)<(x), 有 {un}→u0强收敛于Lq(x)(Ω).利用 Hlder 不等式和嵌入定理, 可得 再利用引理3.6 可得un →u0强收敛于X0, 即泛函Φ 满足(C)- 条件.引理3.7 得证. 因为X0可分自反的Banach 空间, 则存在使得 记Ej=span{ej}, 则X0=⊕j≥1Ej.对任意的k=1,2,···, 记 引理 3.8(见文献[15, 引理3.9]) 设对任意的x ∈Ω 有定义 下面来验证能量泛函Φ 满足喷泉定理中的两个条件. 引理 3.9设p(x,y) 满足 (P1)–(P2),f满足 (f1)–(f4).则存在ρk>rk>0, 使得 证(i) 由 (f1) 和 (f3), 对任意的ε>0, 存在常数Cε>0, 使得 令u ∈Zk, 且选取充分小的ε使得则由 (3.10) 式和引理2.4 (2), 可得 这里的C是互不相等的正常数.令则由引理 3.8 及p−≤p+ 即当k →+∞时, 有得证 (ii) 对任意的u ∈Yk, 设则由引理 2.4 中 (2), 可得 由 (f2)–(f3) 知, 对任意的u ∈Yk, 存在常数Ck>0 使得 因为Yk是有限维的, 所以Yk中的所有范数等价, 从而 定理1.1 的证明利用引理3.7, 引理3.9 及Φ(−u)=Φ(u), 可知泛函Φ 满足喷泉定理的几何结构.从而由喷泉定理(定理3.3) 可得方程(1.1) 在X0中存在一非平凡解列并且该解列满足Φ(un)→+∞(n →∞).定理得证.
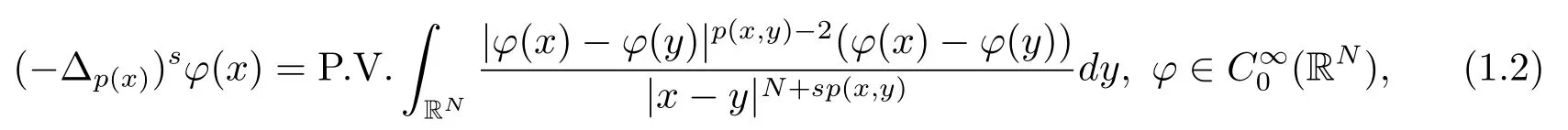
2 分数阶变指数Sobolev空间
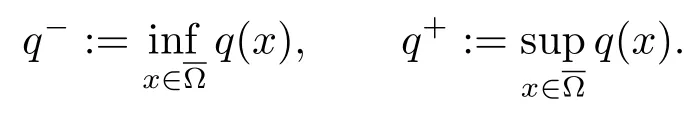



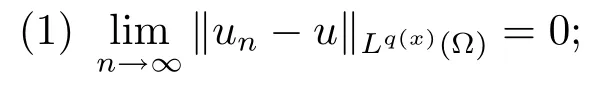
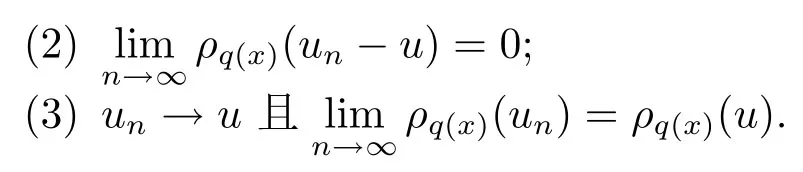

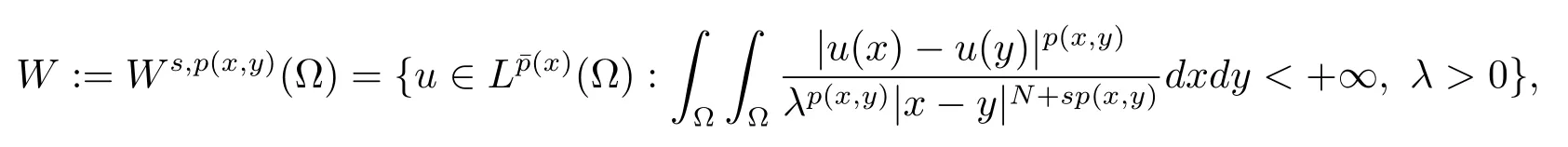

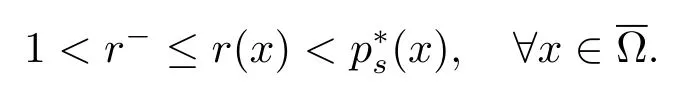


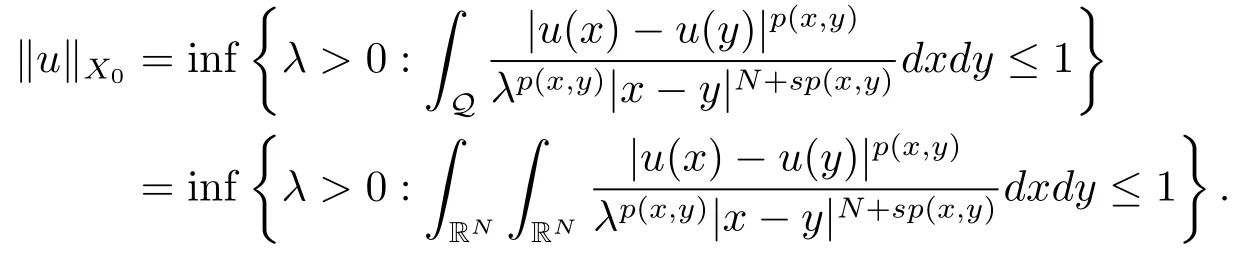
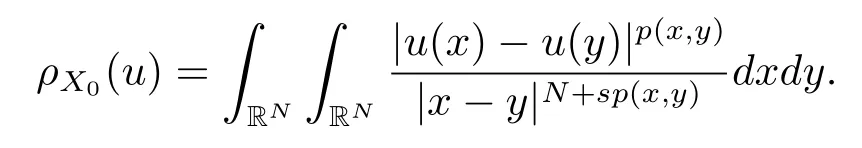
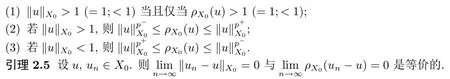
3 主要结果的证明

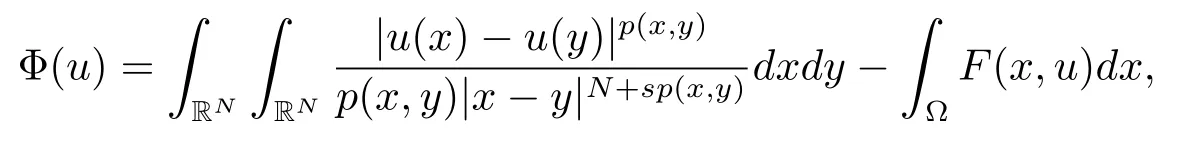


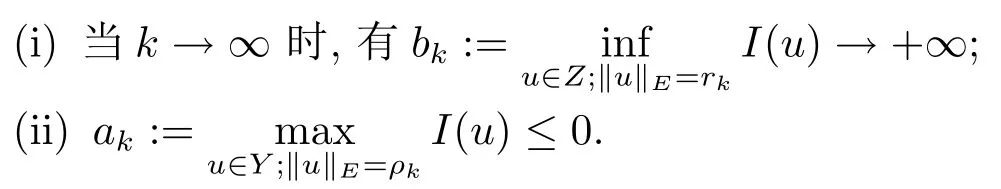
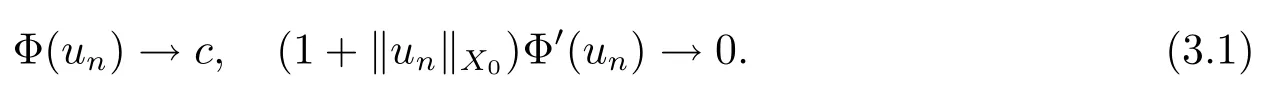
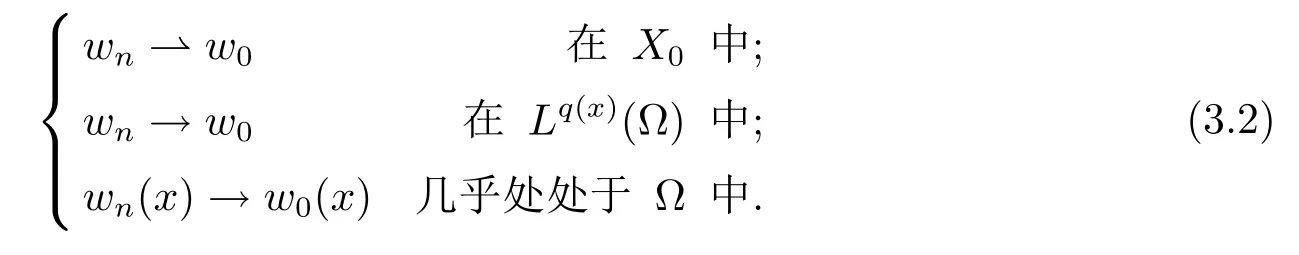


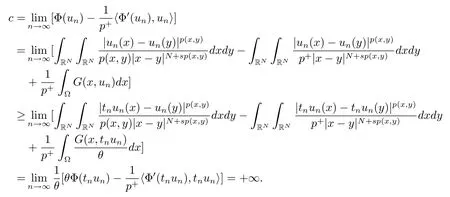
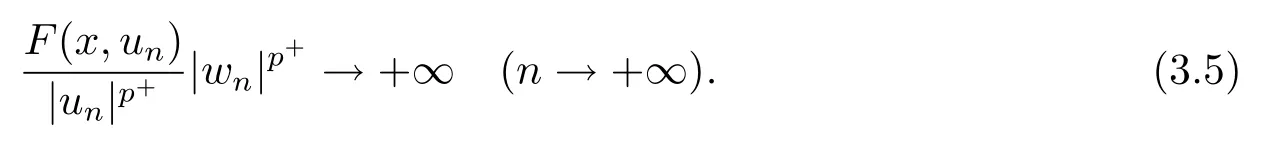
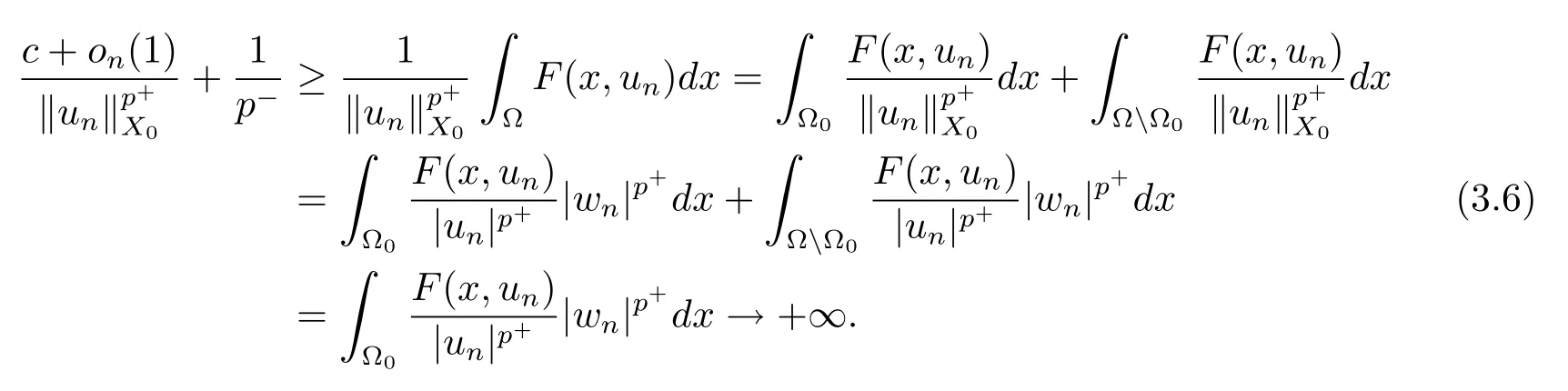
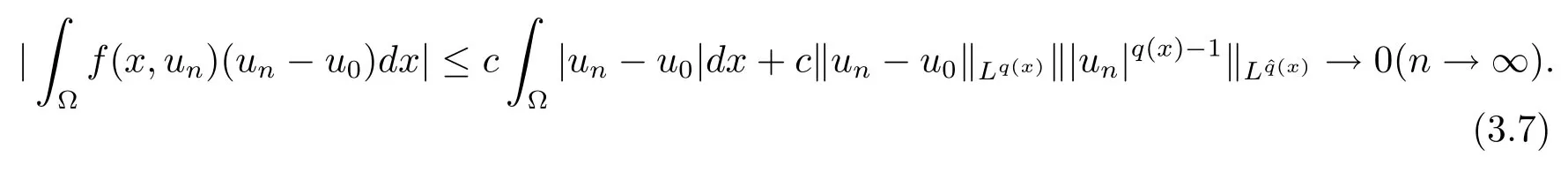

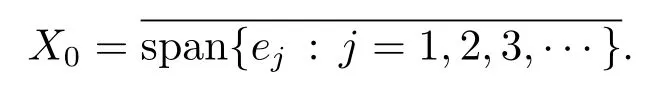

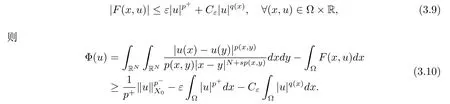
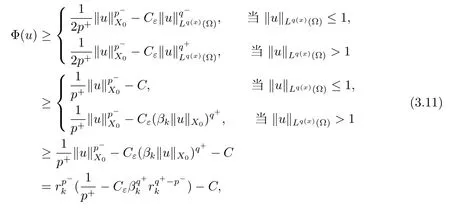
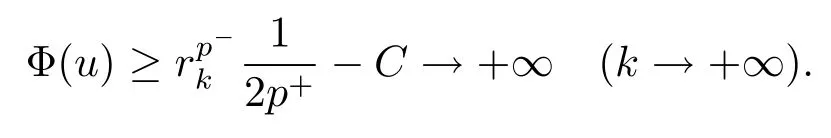


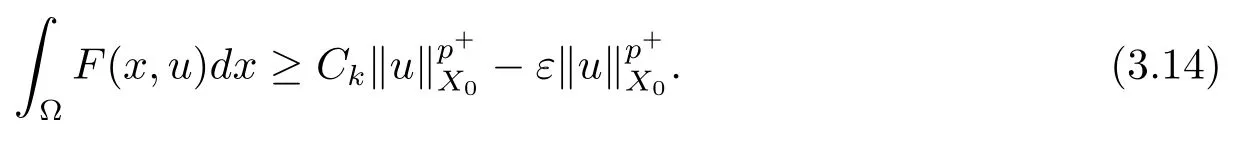
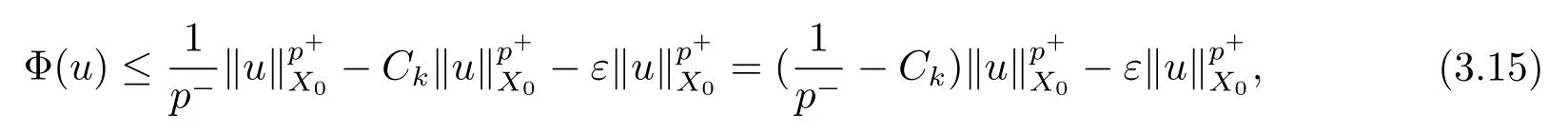
猜你喜欢
杂志排行
数学杂志的其它文章
- LEONARD PAIRS CONSTRUCTED FROM THE QUANTUM ALGEBRA νq(sl2)
- BOUNDEDNESS OF THE FRACTIONAL INTEGRAL OPERATOR WITH ROUGH KERNEL AND ITS COMMUTATOR IN VANISHING GENERALIZED VARIABLE EXPONENT MORREY SPACES ON UNBOUNDED SETS
- IMPROVE INEQUALITIES OF ARITHMETIC-HARMONIC MEAN
- A CLASS OF NON-MATCHABLE DISTRIBUTIVE LATTICES
- SHARP ESTIMATES FOR EIGENVALUES OF BI-DRIFTING LAPLACIAN
- 素的∗-代数上的非线性混合Lie三重ξ-导子
