快速方向字典插值的中低倍率超分辨率算法*

2020-02-20王钟斐

计算机与生活 2020年2期

王钟斐，王彪

宝鸡文理学院数学与信息科学学院，陕西宝鸡 721013

1 引言

随着人们对视频和显示质量需求的逐渐增加，作为视频质量的重要特性，视频的图像分辨率已经逐渐过渡到目前主流市场的4K水平[1-2]。为了满足越来越高的图像分辨率，终端显示设备的分辨率也逐渐加大。但是由于陈旧视频源的分辨率较低，且低分辨率（low resolution，LR）视频源在高分辨率（high resolution，HR）显示设备上不能得到较好的显示效果，因此视频源从LR向HR转化的超分辨率[3-4]（super resolution，SR）技术的研究被广泛关注。

基于当前市场需求，SR应用主要分为两类：一类为视频源从LR直接转化为HR后，通过网络传输且显示[5-7]；另一类为LR视频源通过网络传输后，在显示端转化为HR后显示。可以看出，后者在提高视频分辨率的同时可以节约大量的网络带宽。因此显示端的实时SR技术成为研究的重中之重[8-10]。

目前SR技术主要从现实应用角度分为两种，分别为实时系统中SR和非实时系统中SR，非实时系统中SR代表算法为基于深度学习的方法[11-12]，实时系统中SR代表算法为基于方向插值的方法[13-16]。在基于学习的方法中，典型算法为稀疏矩阵的字典算法，该方法认为LR和HR存在映射关系，通过大量LR和HR数据的训练学习，找到最优的映射矩阵。图像由LR到HR的转化过程中，通过查找对应类型的映射矩阵，实现图像的SR重建。该方法为了获取最优的图像质量，需要存储海量的映射矩阵和边信息，并且运算复杂度极高。由于该方法的海量存储导致实现成本增加，且运算复杂度过大不能达到实时的要求，因此该方法目前不适于工业量产。在基于插值的方法中，典型算法为方向插值算法，该方法首先判断纹理方向，然后根据纹理方向进行插值，得到SR重建图像。该方法通过运算复杂度和图像质量的均衡，在控制成本的前提下，追求图像质量更优。

由于目前片源和显示设备的分辨率倍数差异不会过大，并且考虑到成本，大多实时显示系统的SR分为2～3倍的低倍率和4～5倍的中倍率。

2018年，Kim等提出了基于线性映射的边缘定位超分辨率算法（super resolution using edge orientation based on linear mapping，SREO）[17]。目前该算法为实时中低倍率SR系统的最优算法。该算法首先在LR图像中根据纹理边缘的计算得到大量的纹理方向，然后利用这些纹理方向和HR图像进行映射，训练得到对应的映射矩阵，最终通过映射矩阵查表的方式进行SR的图像重建。虽然SREO在图像质量和成本复杂度之间进行平衡，以达到实时性和实现量产的目的，但是该方法仍存在以下缺点：

（1）较经典的稀疏矩阵的字典算法，由于SREO的映射矩阵数量过少，导致图像质量下滑严重。

（2）较方向插值算法，SREO的映射矩阵需要大量的存储空间，且浮点型矩阵映射运算的复杂度极高，因此实现成本大幅度增加。

基于以上问题，针对实时显示系统，本文提出了一种纹理字典和全方向插值的中低倍率快速超分辨率算法（directional dictionary and fitting interpolation，DDFI）。该算法通过金字塔纹理字典和方向矫正，为每个待插值像素（interpolated pixel，IP）的位置计算插值方向，并通过单边拟合的方向插值得到IP的像素值，最终在进一步提高图像质量的同时，减少运算复杂度。

2 SREO算法

2.1 算法介绍

以2倍的低倍率SR为例，实际工作之前，SREO在先验的原始HR图像和LR图像之间，计算得到625组映射矩阵模型。实际工作之后，SREO首先对LR图像的每个像素，在625组映射矩阵模型中查找对应的模型；然后采用该模型，对该LR像素进行映射得到对应的HR像素；依次循环，最终得到SR重建图像。具体步骤如下：

步骤1将先验的HR图像，以固定倍率进行下采样得到LR图像。

研究表明，草33薄层稠油油藏在水平井井网条件下具备蒸汽驱可行性。但为了稳妥起见，建议实施井组矿场试验，在取得经验的基础上大规模推广，同时在试验过程中需要加大监测资料的录取和分析，及时配套工艺技术解决现场的开发问题。

步骤2如图1所示，通过HR图像中IP位置反推，得到LR图像中基准像素位置。将基准像素和其周围共9个像素抽取，形成1个3×3的大块后，分割为4个2×2的子块。

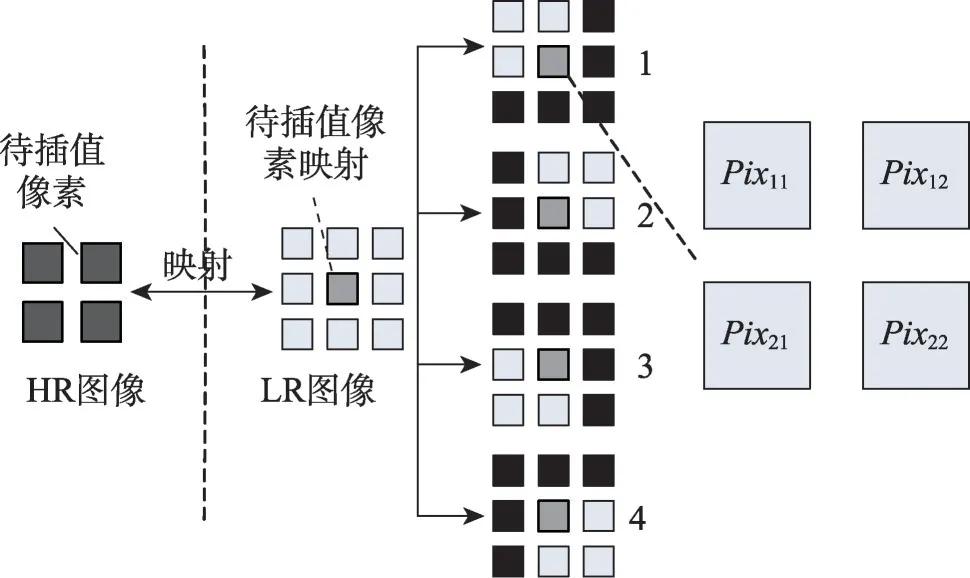
Fig.1 Direction calculation diagram using 3×3 pixels in SREO图1 SREO中3×3像素方向计算示意图

步骤3根据式（1）对每个子块进行水平梯度gh和垂直梯度gv的计算。与图1对应，式中表示第i个子块中第x列第y行的像素。

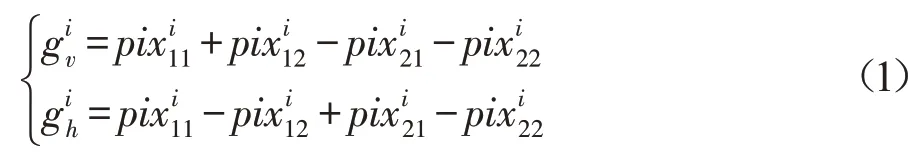
将计算结果带入式（2），计算边缘方向。式中，mi和di分别是第i个子块的梯度权重和梯度斜率。

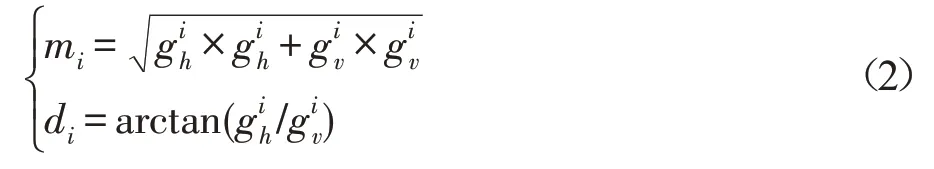
根据计算结果和预定义阈值，在表1中查询得到每个子块的纹理方向和索引。

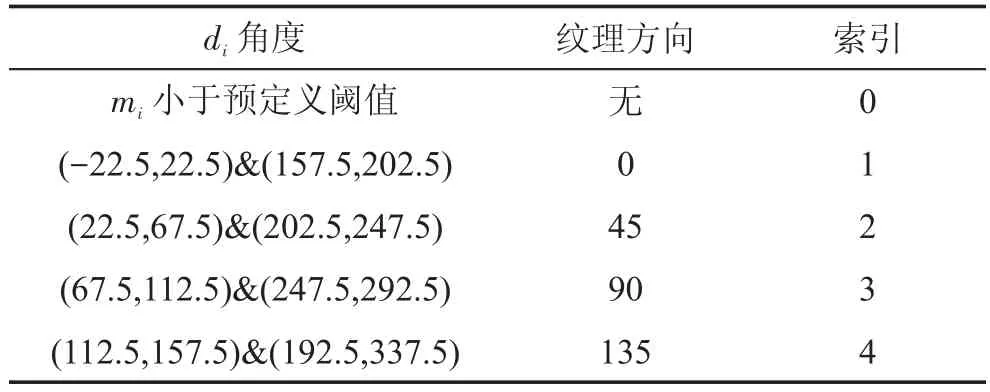
Table 1 SREO subpatch direction map table表1 SREO子块方向映射表

步骤4将4个子块的索引组成2×2矩阵X。设HR图像的2×2矩阵为Y，映射矩阵为M。为了最小化M和Y之间的误差，考虑Y的多样化，采用多变量回归模型，通过式（3）计算一个最优的M，其中λ为归一化参数，I为正则矩阵。

由于每个子块的方向可能性为5种，因此对于2倍率SR，4个子块的方向组合为54种，即可得到625种映射矩阵模型。

在所有映射矩阵模型得到后，SREO实际工作时，首先对于HR图像中IP，计算LR图像中对应的待插值像素映射（interpolated pixel map，IPM）位置；然后采用式（2）计算基准像素的mi和di，形成索引矩阵后，查表选取对应的映射模型进行映射；最终得到SR后的HR像素。以此类推，若为4倍SR，则映射矩阵数量为516。

2.2 问题分析

根据以上算法介绍，可以看出SREO有如下问题：

（1）图像质量角度。SREO仅采用5种纹理方向，远不能够满足自然界的纹理复杂情况，2倍率SR下SREO的625组映射矩阵，较经典的稀疏矩阵的字典算法，也不能使映射矩阵达到最优。因此SREO的图像质量较稀疏矩阵的字典算法有较大差距。

（2）实现成本角度。2倍率SR下，SREO的625组映射矩阵需要大量的存储空间，且每个像素浮点型矩阵映射的运算复杂度偏高。因此较插值算法，SREO实现的成本大幅度增加。

（3）规格角度。SREO针对2倍的低倍率SR进行设计，对于中倍率情况，不仅较少的纹理方向会引起重建HR图像质量的下降，而且成指数级增长映射矩阵的数量也会使SREO的实现成本不可接受。

针对以上问题，本文提出了DDFI算法。

3 DDFI算法分析

3.1 金字塔字典映射模型

如图2所示，根据在HR图像中的IP确定其在LR图像中的IPM，并以由IPM确定的Pix22、Pix23、Pix32和Pix33构成的2×2区域为插值区域。将该2×2区域分别拓展为4×4和6×6区域，形成3层金字塔模型。先根据式（4）计算得到3层的4个方向的梯度权重，式中i和j分别为像素点的行列坐标，k为层数。再根据式（5）计算得到4组梯度比。

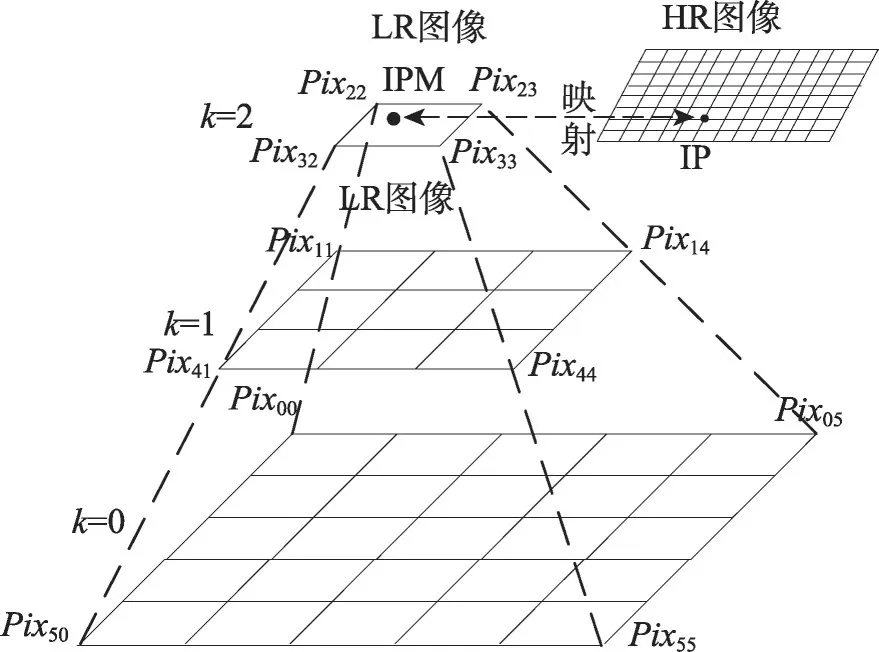
Fig.2 Pyramid model图2 金字塔模型

根据层数约束后，0层、1层和2层的4组梯度比分别有16、81和256种组合，3层共有331 776种组合。

HR图像中的IP纹理方向dirt计算公式如式（6），dirt为某一方向的梯度权值，IPi为当前IP，IPi-n和IPi+n为当前IP按该方向的前后两个IP，m和n为参数。最终dir对应的角度为该IP的纹理角度。

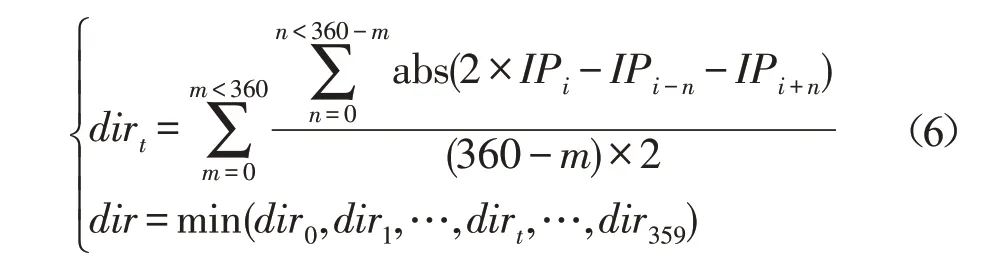
为了确定LR图像中IPM的331 776种组合和HR图像中IP的360个角度的对应关系，在固定SR倍率下，首先仿真约100万幅HR图像和之对应的LR图像，得到IPM每个组合对应的所有IP角度；然后对于1种IPM组合，在其对应的所有IP角度中，选取出现概率最大的角度，作为该IPM组合的对应角度；以此类推，得到所有IPM组合的对应角度。最终，在实际工作之前形成一个331 776组合和360°的方向映射表。

3.2 IP的插值方向

实际工作中，首先确定IP的插值方向，具体如下：

步骤1插值区域主方向的确定

由于自然图像中大部分区域为平坦区域，为了降低运算复杂度，在IPM的插值区域中，当均小于预设阈值时，确定该区域无方向；否则根据式（5）计算4组梯度比，通过方向映射表得到当前插值区域的主纹理方向。

对于无主纹理方向的插值区域，采用双线性插值的方法得到IP，否则进入步骤2。

步骤2IP方向矫正

对于存在纹理主方向区域，由于插值区域中所有IPM并非严格同一方向，而是基于一个方向的方向簇，因此对于任1个IPM，需要考虑其相邻插值区域的主纹理方向。如图3所示，插值区域分为8个子区域，每个子区域需参考1个直相邻和1个斜相邻区域的主纹理方向。设插值区域为正方形，且每个边长为100，可得对角长度为141。设t为IPM到当前插值区域斜对角线的垂直距离，a为IPM到当前插值区域中线垂直距离。根据式（7）计算得到IPM的具体方向。

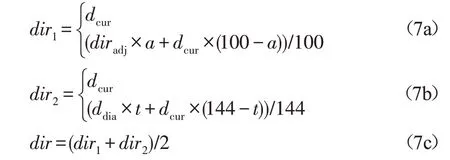
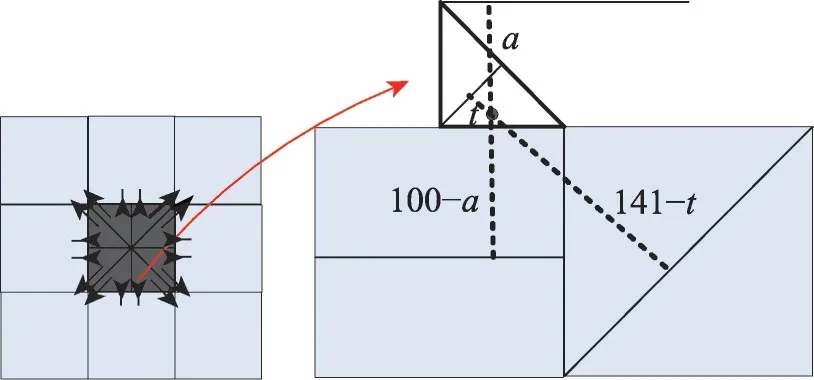
Fig.3 Direction correction图3 方向纠偏

式（7）中，条件为相邻区域主纹理方向为无方向或相邻区域与当前插值区域主纹理方向差异超过45°。dcur、dadj和ddia分别是当前、直相邻和斜相邻的区域的主纹理方向。

3.3 拟合插值

对于高次运算插值算法，如双立方插值（bicubic interpolation，BC），虽然图像质量更优，但是复杂度过高；当中低倍率SR时，相对高次运算插值算法、低次运算插值算法效果相近且复杂度更低。对于存在纹理主方向区域，考虑到算法的实时性和低复杂度，为了拟合曲线，本文采用单边拟合插值的方法。如图4所示，先利用水平或垂直单边拟合插值计算得到IPM方向上4个子像素点，再利用这4个子像素点，进行第二次单边拟合插值，最终得到IPM对应的IP。单边拟合插值公式如式（8）：

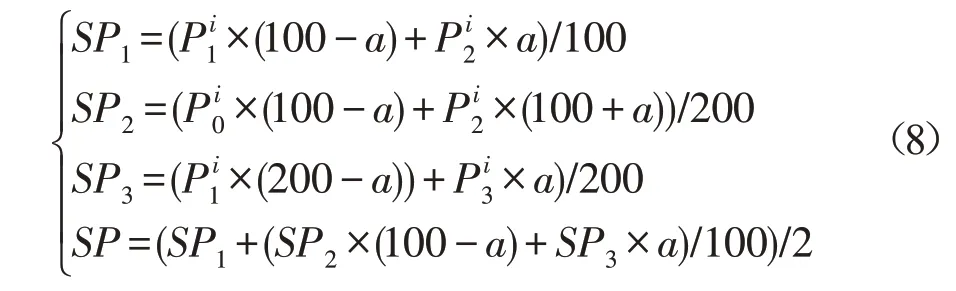
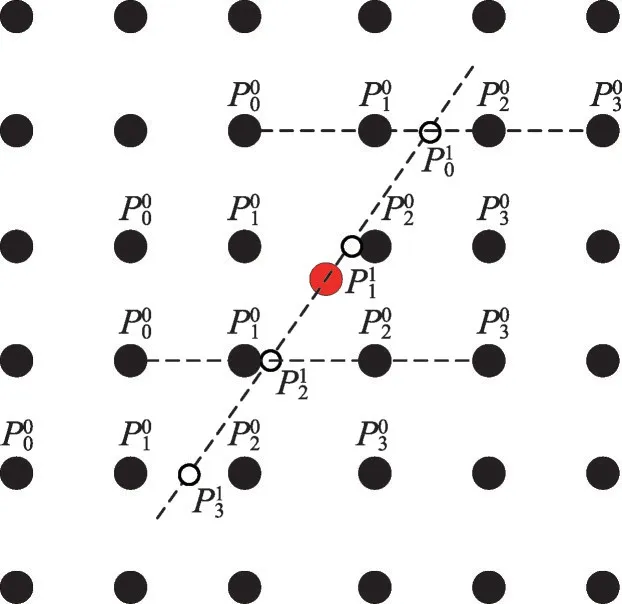
Fig.4 Interpolation schematic diagram图4 插值示意图

根据以上算法原理描述，可以看出本文算法较传统插值算法，引入金字塔方向字典映射，在SR实际工作之前，获得更准确的方向查询模型，在SR实际工作中可得到更准确的纹理方向判定。较SREO，不但具有更多的纹理主方向，而且插值区域内形成了多方向的方向簇，更符合自然图像形成规律，而且运算复杂度较低。

3.4 复杂度分析

以2倍SR为例，SREO对于每个IPM，索引矩阵的形成需要28个加法器，4个乘法器，1个求根处理和1个查表运算；查表之后的矩阵映射运算需要8个乘法器和4个加法器。平均求根和查表处理运算后，SREO共需要约50个乘法和32个加法。本文算法对于每个IPM，当具有纹理方向时，运算复杂度最高，方向判定阶段最高需要约120个加法器，15个乘法器和1个查表运算；插值阶段需要10个乘法器和5个加法器。平均查表处理运算后，本文共需要约50个乘法和32个加法，共需要40个乘法器和125个加法器。可以看出，本文算法的最大计算量与SREO基本持平，但是本文算法对于所有计算，均限制最大8比特精度，远小于SREO的16比特精度，因此本文算法的计算复杂度较SREO更低。

4 实验结果与分析

本文根据图像质量和运算复杂度对算法进行测试，其中图像质量包括主客观图像质量，客观图像质量分为PSNR和SSIM；运算复杂度以运行时间（run time，UT）进行衡量。对比算法选取典型插值算法BC（bilinear interpolation）、典型深度学习算法RAISR（rapid and accurate image super resolution）[18]和SREO。SR倍数分别设置为2倍和4倍，运行平台为Intel I5-6400 CPU@2.7 GHz-8 GB内存-Win 7 64位系统。选取的测试序列为经典测试序列和如图5所示的实际采集到的测试序列。

实验结果如表2所示。较BC，由于有了纹理的方向判定，图像质量更有大幅度提高，平均PSNR和SSIM分别提高1.4 dB和0.047；运算复杂度方面，本文算法虽然对纹理区域的方向判定消耗了大量的运算，但是平坦区域不需要方向判定且插值方法简单，而且拟合插值算法较BC的3次运算也节省了大量的运算量，因此平均运算复杂度为BC的58.3%。

较RAISR，本文算法虽然PSNR和SSIM提高较小，但是算法运算量仅约为RAISR的2%。即无论在硬件系统还是软件工程，RAISR目前是无法做到实时计算显示的。且由于RAISR需要海量数据的存储，也是不可工业化实现的。

Fig.5 Captured images sequence图5 采集到的图像序列

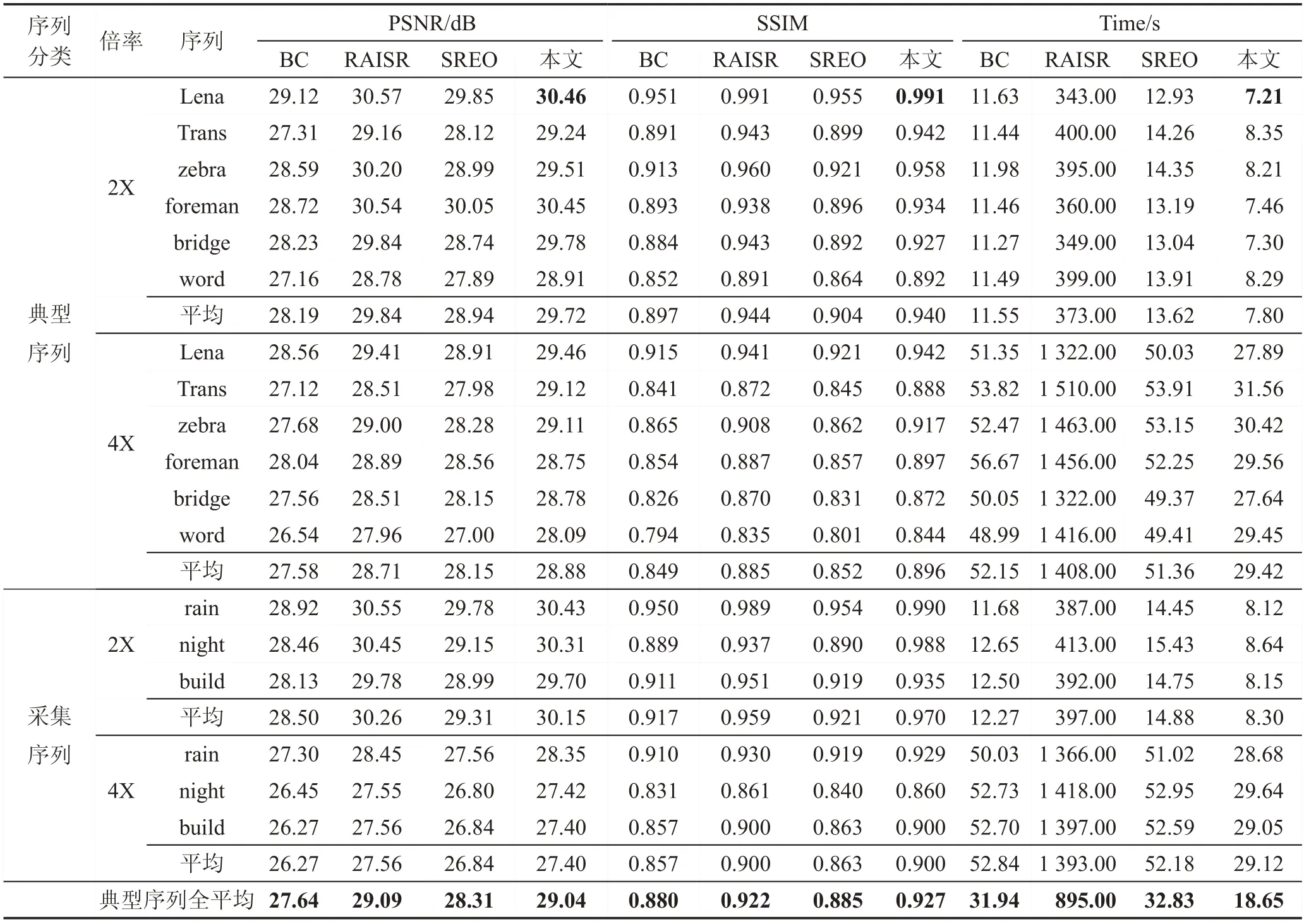
Table 2 Performance comparison among BC，RAISR，SREO and the proposal表2 BC、RAISR、SREO和本文算法的性能比较结果

较SREO，由于本文算法采用更高准确率的纹理方向判定与拟合插值算法，因此平均PSNR和SSIM分别提高0.73 dB和0.042；由于SREO的4倍SR较2倍SR矩阵浮点乘运算呈指数级增加，因此4倍SR时，本文算法运算量仅约为SREO的56.8%。

主观图像质量对比如图6所示，较BC和SREO，可以看出本文算法在纹理细节区域处理得更好，对于图中头发区域，本文算法的细节纹理更加丰富锐利。

5 总结

针对SREO的问题，为了进一步提高重建图像质量，并且降低运算复杂度，提出了DDFI算法。DDFI首先采用金字塔纹理字典得到插值区域纹理主方向，然后根据IPM的位置矫正得到IP的纹理方向，最后采用单边拟合的方向插值算法计算IP值。实验结果显示，与SREO相比，本文算法的PSNR和SSIM平均分别提高了0.73 dB和0.04，同时大幅度降低了运算复杂度。