解决深度探索问题的贝叶斯深度强化学习算法

杨 珉，汪 洁

中南大学 信息科学与工程学院，长沙 410083

1 引言

强化学习领域最主要的三大问题[1]分别是：（1）泛化；（2）如何平衡探索与利用之间的关系；（3）信用分配问题（credit assignment problem）。近几年的研究热点主要集中在大规模状态空间下的泛化问题，并有了一个新的研究领域，名为深度强化学习[2]（deep reinforcement learning）。该领域的兴起是从DeepMind团队提出DQN（deep Q-network）算法[3]后开始的，DQN算法最主要的贡献就是将深度学习[4]和强化学习[5]结合起来，并通过经验回放（experience replay）和目标网络机制来解决有关泛化的一些问题[6]。此后，也有很多关于DQN算法的改进版本被提出来[7-8]，这些算法主要关注的还是泛化问题，而本文要探讨的主要问题是如何平衡探索与利用之间的关系。

机器学习领域中最热门的监督学习算法只能从人类收集到的数据中学习相关的模式，然而需要收集什么样的数据，或者说哪些数据是重要的还是需要人类来决定。强化学习可以通过选择不同的动作得到不同的观察序列，然后根据得到的观察序列学习相关的模式，也就是说，在强化学习的范畴内，需要算法来决定是选择当前最优的动作（利用）还是选择有可能带来长期利益的动作（探索）。然而DQN等算法使用的是简单的启发式探索策略ε-贪婪，该策略只以ε(0 ≤ε≤1)的概率随机选择一个动作，以此来达到探索的效果，然而这样的探索策略是极其低效的。虽然DQN算法能在街机学习环境[9]（arcade learning environment）中达到甚至超过人类水平，但是在面对深度探索问题（参见第4章）时，算法的时间复杂度为O(2N)。好的探索策略必须要考虑所选择的动作所带来的信息增益，而信息主要是通过估计值的不确定程度来衡量的，那么只需引入概率思维就可以得到一个好的探索策略。其实早在1998年，Dearden等学者就提出了贝叶斯Q学习[10]来平衡探索与利用之间的关系。此后，也有其他研究人员提出了贝叶斯框架下的强化学习算法[11-12]，然而这些算法的计算过程比较复杂，而且无法和深度学习技术结合起来。贝叶斯强化学习和深度学习结合最主要的问题是：在高维状态空间下，得到神经网络参数的后验分布是棘手的（intractable）。本文的贡献就在于提出了一种新的计算方法，该计算方法可以产生参数后验分布的样本（参见第5章），将使用了该计算方法的深度强化学习算法统称为贝叶斯深度强化学习算法。目前而言，该计算方法只适用于基于值的深度强化学习算法，同基于策略的深度强化学习算法的结合需要进一步的研究。将Bootstrapped DQN[13]和该计算方法结合，得到新的算法BBDQN（Bayesian Bootstrapped DQN），并通过两个环境下的实验来验证算法的探索效率，其中一个实验环境是具有深度探索结构的格子世界；另一个实验环境是经典控制问题Mountain Car，该问题本身不具备深度探索结构，对其奖励函数稍作修改使其具备深度探索结构，然后在修改后的Mountain Car上进行实验。实验结果显示BBDQN可以解决深度探索问题，并且其探索效率要优于使用随机探索策略（即ε-贪婪）的DQN算法以及Bootstrapped DQN算法。

2 相关工作

强化学习算法的探索效率直接影响到算法的样本效率，提高探索效率可以降低训练智能体所需的时间步数。贝叶斯最优策略（Bayes-optimal policy）是衡量强化学习算法的探索效率的一个标准，然而计算贝叶斯最优策略是棘手的，因为计算时间随问题空间（状态和动作）呈指数级增长[14]。考虑探索效率方面的研究非常多，而最早提出的是Kearns和Singh[15]，他们的工作确认了多项式时间的强化学习算法必须用到多周期探索（multi-period exploration）。基于他们的工作，一系列表格（tabular）强化学习算法被提出来[16-22]，这些论文中提到的探索方法都要比ε-贪婪和玻尔兹曼探索要高效，但是这些方法都无法处理维数灾难（curse of dimensionality）。近几年提出的处理大规模状态空间的深度强化学习算法[3，23-24]偏向于使用ε-贪婪探索，这些算法在Atari街机游戏以及围棋上能得到很好的结果，然而却没有任何实际方面的应用，低效的探索效率使得这些算法只能在模拟环境中训练。

针对大规模状态空间下的探索，有研究人员提出了模型学习算法[25]，该方法的问题在于只能解决简单的模型类问题，对于复杂的模型，该方法的计算也是棘手的。有研究人员提出了策略学习算法[26]，该类算法主要解决的是连续动作空间问题，如机器人控制，但是当策略空间的大小是指数级的时候，该方法就无法保证探索的效率了。还有一类方法是根据伪计数（pseudocount）[27]或密度模型[28]给不常访问的状态分配奖励，以此来达到鼓励探索的目的。

如何保证算法的探索效率和泛化一直是强化学习的一个难题，也有研究人员想到了使用贝叶斯思想处理这一问题，比如贝叶斯Q学习算法[10]，然而该算法只能处理状态数量有限的问题；还有Osband等人[29]提出的RLSVI（randomized least-square value iteration）算法，该算法只适用于线性函数逼近器，无法和神经网络这一非线性函数逼近器相结合；而Azizzadenesheli等人[30]提出的算法将神经网络作为特征提取器，将网络的最后一层的输入作为特征，然后使用贝叶斯线性回归计算Q值。贝叶斯神经网络方面的研究一直未成为主流[31-32]，然而最近有复苏的迹象，有许多关于量化数据集的不确定性的方法[33-35]被提出来，本文作者受到这些方法的启发，提出了一种可以有效计算贝叶斯后验的深度强化学习算法。

3 背景知识

强化学习问题通常建模为马尔可夫决策过程，本文使用的马尔可夫决策过程可以表示为(S,A,T,R,γ)，其中S为状态空间；A为动作空间且A(s),s∈S为状态s下可用的动作集；T为状态转移概率，T(st+1|st,at)表示在状态st下采取动作at后转移到状态st+1的概率；R为奖励函数，用Rs,a表示在状态s下采取动作a后得到的奖励分布的均值，用r表示状态s下采取动作a后得到的立即奖励（也可以理解为从奖励分布中得到的样本），则有Rs,a=Ε[r|st=s,at=a]；γ∈[0,1)是折扣参数，用来控制未来奖励所占的权重。

强化学习的目标是学习一个策略使得智能体所获得的折扣累积奖励最大化。用π来表示策略，且π(a|s)表示在状态s下采取动作a的概率。然后引入动作值函数（Q函数）的概念，动作值函数Qπ(s,a)表示在策略π下，智能体在状态s下采取了动作a后所能获得的期望折扣累积奖励，即：

该方程也可以通过递归的形式表示出来：

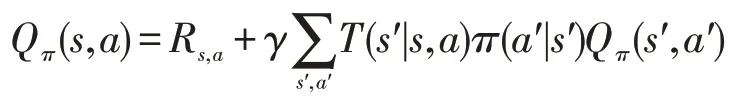
用π*表示最优策略，用Q*表示最优动作值函数。由于最优策略就是能获得最大折扣累积奖励的策略，因此可以将Q*函数写为：

式（1）也称作贝尔曼最优方程（Bellman optimality equation），对于每一对s,a，都有一个方程，将所有这些方程联合起来就得到了一个方程组，通过线性规划方法可以求解这个方程组得到所有s,a对应的最优动作值函数Q*(s,a)。也可以通过策略迭代（policy iteration）或者值迭代（value iteration）等动态规划方法求解最优动作值函数。最优策略可以通过最优动作值函数表达出来，即对于所有状态s，选择该状态下使得最优动作值函数最大的动作，如果有多个动作满足这一条件，可以从这些动作中随机选择一个。从式（1）中可以看到，这种方法需要已知环境模型——状态转移概率T和奖励函数R——才能计算出来，在不知道环境模型的情况下就需要通过其他方法来求最优策略，比如Q学习算法。Q学习是通过迭代方式来计算最优动作值函数的，更新规则为：

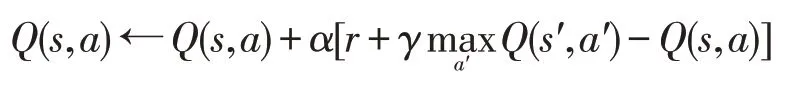
其中，α为学习率，奖励r和下一状态s'都是环境反馈给智能体的，在状态空间和动作空间有限的情况下，只要学习率序列满足随机近似条件且所有状态-动作对都能得到持续更新的情况下，该算法以概率1收敛到最优值函数Q*[5]。

在大规模状态空间下，传统的强化学习算法Q学习不再适用，但是可以通过结合函数逼近技术来解决这一问题。神经网络和强化学习的结合是近几年研究的热点，而DQN算法就是这方面的典范。当使用神经网络时，动作值函数可以表示为Qθ(s,a)，其中θ是神经网络的参数。通过与环境交互得到的反馈信息来计算目标值：

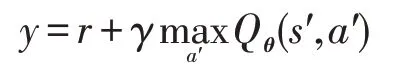
有了目标值和预测值就可以通过随机梯度下降算法更新神经网络的参数θ，更新规则为：

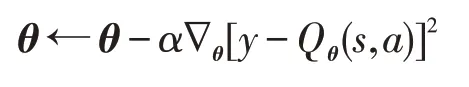
如果直接这样做的话，效果并不是很好，因为神经网络是监督学习方法，要求各个训练样本之间是相互独立的，强化学习收集的样本之间是相互关联的，而且每次更新参数会影响到目标值，导致目标值不稳定。正如DQN算法中所提到的，只需要两个机制就可以缓解这一问题：经验回放和目标网络。经验回放机制就是每次智能体与环境交互时，将该次交互的信息(s,a,r,s′)存入记忆池（replay buffer）中，每次更新时智能体从记忆池中随机抽取一定数量的样本，并用这些样本来更新参数。目标网络机制就是智能体维护两个Q网络，一个网络是用来选择动作并实时更新的，另一个网络（目标网络）用来计算目标值并且不会实时更新，每次更新时使用的目标值可以表示为：

其中，Qtarget表示目标网络，只有过了指定的时间步后，才将两个网络的参数同步一次。

4 深度探索问题

文献[10]中提到的链问题就是一类深度探索问题，本章将用该问题来分析ε-贪婪策略和玻尔兹曼探索的探索效率。为了计算简便，对文献[10]中的链问题做出了一定的修改。

ε-贪婪探索就是有ε的概率从所有可用的动作中随机选择一个，有1-ε的概率选择就当前而言最优的动作。玻尔兹曼探索选择每个动作的概率和动作值函数的估计成正比，计算公式为：

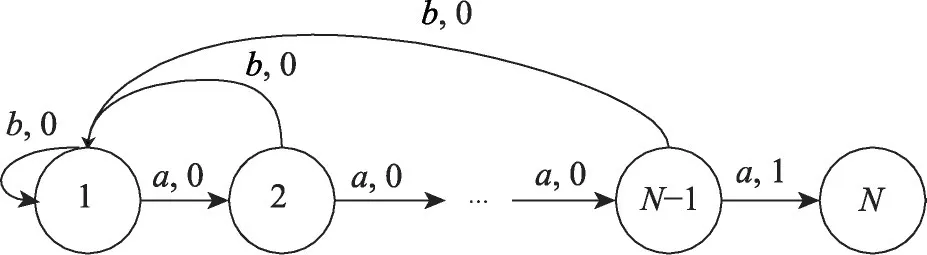
Fig.1 Chain problem图1 链问题

使用一个链问题来分析ε-贪婪探索和玻尔兹曼探索的探索效率，该问题的状态转换图如图1所示，图中每一条箭头都对应一个动作以及奖励，该问题的起始状态为1，终止状态为N。假设每个周期（episode）的长度H=N-1，并且无论在哪个状态下，选择动作a会有0.2的概率失败（失败意味着选择的动作和实际动作不一致），而动作b是确定性的。这个问题的最优策略就是一直选择动作a，最优策略每个周期所能得到的平均奖励就是该策略成功到达N的概率(1-0.2)N-1。无论是ε-贪婪探索还是玻尔兹曼探索，由于到达目标状态N之前没有奖励（即奖励为0），因此所有状态下动作a和动作b的估计值都是相等的，动作选择完全是随机的，这种情况下通过探索到达状态N的概率为(1-0.2)N-1×2-(N-1)，只需取该概率的倒数就能得到通过探索到达状态N平均所需的周期数量，用l代表所需的周期数量，则有如下关系成立：

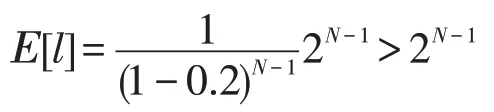
根据该不等式，可以确定使用ε-贪婪策略或玻尔兹曼探索的强化学习算法在面对链问题之类的深度探索问题时，其时间复杂度为O(2N)，其中N代表问题的规模。

5 贝叶斯深度强化学习

探索的好处可以用信息的价值估计，所谓信息的价值即指探索所获得的信息导致未来决策质量提升的程度，而如何量化探索所获得的信息是关键。根据信息论，可以用探索所选择的动作的估值的不确定程度来计算该次探索所带来的信息量。在文献[10]中，就提出采用贝叶斯方法来维持这一信息，然而在该篇论文中，所讨论的问题的状态动作对的数量有限，可以通过记录每一个状态动作对获得的所有的回报，然后计算方差，再计算信息量。当状态动作对数量过大时，强化学习会考虑结合泛化技术来解决这一问题，如果使用的是线性函数逼近器，可以根据文献[36]中提到的贝叶斯线性回归来得到估值的方差。但是近几年和深度学习相关的研究表明，神经网络强大的泛化能力远强于线性函数逼近器的泛化能力，因此结合深度学习和强化学习技术成了一大趋势，并产生了一个新的研究领域被称作深度强化学习。由于神经网络结构复杂，且参数数量十分庞大，无法通过文献[36]中提到的计算方法来计算估值的方差，因此本文提出了一种新的计算方法。该方法在每一个时间步通过计算得到神经网络参数的后验分布的一个样本，由于不同动作的估值方差不同，方差高的动作其信息量越大，同时其采样值也可能更大，因此被选择的概率也越高。举个例子，有两个动作，其Q值服从高斯分布，由于动作1被选择的次数更多，因此其方差要小于动作2，假设动作1的方差为1，动作2的方差为10，此外动作1的历史回报均值为3，动作2的历史回报均值为1，因此动作1服从均值为3方差为1的高斯分布，而动作2服从均值为1方差为10的高斯分布，结果就是动作2由于方差大，其采样值大于动作1的采样值的概率也更大。接下来详细介绍如何在深度强化学习算法中应用贝叶斯方法。

神经网络的输入既可以是一维数组，也可以是二维矩阵，甚至可以是三维图像。为了表示清晰，用x∈ℜd表示状态特征，也就是神经网络的输入值，加上目标值y组成训练集，表示为。首先计算线性回归模型参数的后验分布，稍后再将其扩展到神经网络的情形下。模型参数表示为θ∈ℜd，且假设参数θ的先验分布为，观察到的目标值有一定噪声，即yi=θTxi+wi，其中wi∝N(0,σ2)为噪声，各个样本的噪声是相互独立的。根据贝叶斯定理参数θ的后验分布可以表示为：

在贝叶斯理论中，p(D|θ)被称为似然，p(θ)被称为先验，p(D)被称为证据。根据文献[36]的推导，参数θ的后验分布服从均值为式（2）、协方差为式（3）的多元高斯分布：

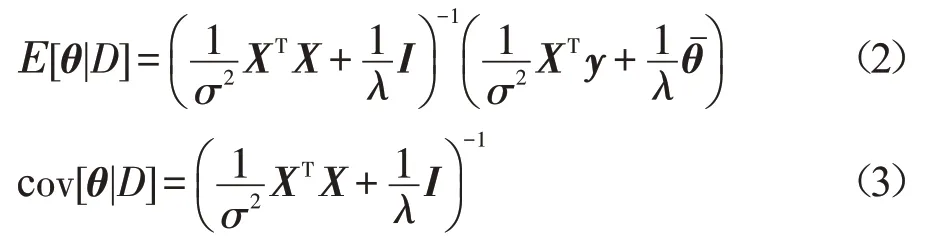
其中，X∈ℜn×d为n个样本输入xi拼接后得到的矩阵，y∈ℜn为n个目标值yi拼接后得到的向量。可以通过马尔可夫链蒙特卡罗等方法推断出该后验分布，但为了扩展到非线性模型人工神经网络，将后验分布用另一种形式表示出来：

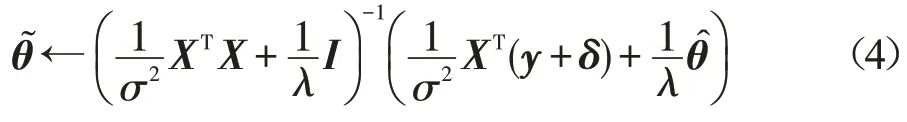
其中，δ∈ℜn是一个随机向量，其每个分量δi都来自高斯分布N(0,σ2)，且各分量的采样是相互独立的，来自参数先验分布。可以证明，和θ是等价的，因为：

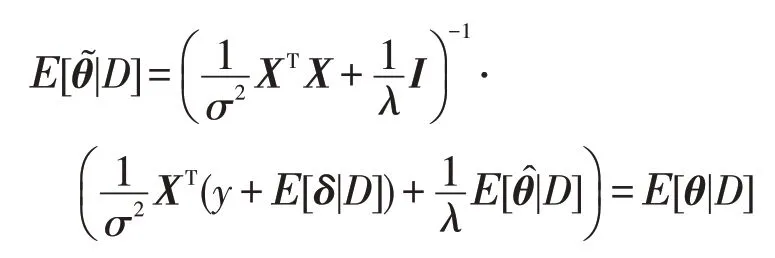
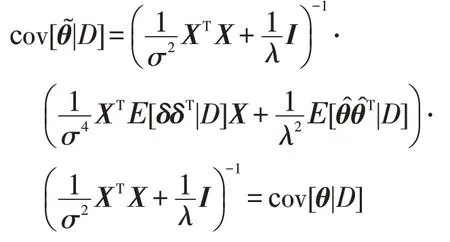
将贝叶斯方法和Bootstrapped DQN结合起来的方法称作BBDQN算法，该算法的整体描述见算法1。

算法1BBDQN算法

输入：折扣参数γ，批量大小n，学习器数量K，参数先验均值，参数先验方差λ，采样间隔Tsample，目标网络更新间隔Ttarget。

6 实验分析

6.1 格子世界

首先在如图2所示的格子世界中测试BBDQN算法的探索效率，白色部分的格子代表网格世界的规模，灰色格子为终止状态，由于空间限制，图2中的格子世界的规模仅为4×4，而在实验中使用的格子世界的规模为20×20，但这并不妨碍使用图2的小规模格子世界来描述其动态模型。图2中状态S为起始状态，且智能体一直保持一个向右行进的速度+1，在每个状态中可供选择的动作是up和down，即向上和向下，如果选择向上，则下一步会到达当前状态的右上状态，如果选择向下，则下一步会到达当前状态的右下状态。如果智能体处于格子世界的底部，则向下动作可以理解为贴墙行进，此时下一状态将处于当前状态的右方，如果在白色格子的右上角选择动作up就能到达灰色格子的顶部，并获得+1的奖励，其他状态都没有奖励，因此要想获得奖励必须一直选择动作up，然而动作up是有代价的，该代价是和格子世界的规模相关的。假设格子世界的规模为N×N，则每一次选择动作up会带来-0.01/N的奖励，而选择动作down没有代价，奖励为0。其实该问题就是第4章提到的链问题的二维扩展版本，可以将输入表示为一个one-hot矩阵xi∈{0,1}N×N，矩阵中智能体所在的位置为1，其他位置全为0。在该实验中，将同使用ε-贪婪策略的DQN以及Bootstrapped DQN进行比较，BBDQN算法用到的超参数显示在表1中，其中0 ∈ℜd代表分量全为0的一个向量。

Fig.2 Gridworld with deep exploration structure图2 具有深度探索结构的格子世界

Table 1 Hyperparameters表1 超参数

实验结果显示在图3中，图中是用遗憾（regret）来衡量算法性能的。遗憾是指最大累积奖励与实际累积奖励之间的差值，该指标越小算法性能越好。因为DQN一直没有发现格子世界中存在奖励的区域，因此其累积奖励小于0，其遗憾在不断地增长。从图3中可以看到，BBDQN只需不到2 000个周期就可以学习到最优策略，而DQN在10 000个周期后都没有学习到一个好的策略。事实上，进行了100万个周期的实验，DQN依然没有收敛。

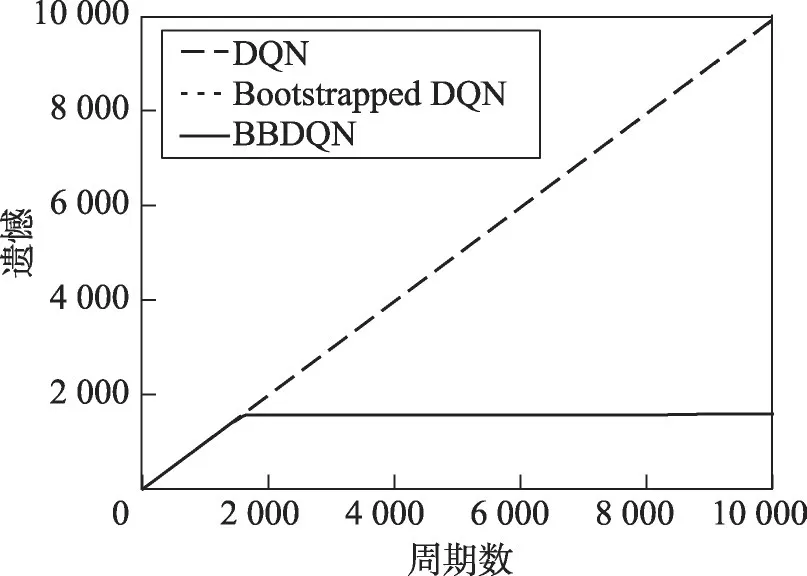
Fig.3 Comparison of algorithm performance in Gridworld图3 格子世界上算法性能比较

正如第4章所分析的那样，使用ε-贪婪策略的DQN算法在面对深度探索问题时，算法的时间复杂度为O(2N)。本文还测试了Bootstrapped DQN算法的性能，该算法的动作选择不是通过ε-贪婪实现的，而且该算法是通过在DQN的基础上加入集成技术来提高其探索效率的[13]，但也无法在短期内解决该深度探索问题。Bootstrapped DQN和DQN在10 000个周期内的遗憾只有微小的差异，该差异在图3中看不出来，必须放大才能看出区别，具体地讲，DQN在10 000个周期中累积的遗憾为9 922.02，Bootstrapped DQN为9 914.60。

图3是当格子世界的规模为20×20时，算法的性能曲线。可以假设格子世界的规模为N×N，并分析算法探索效率和N之间的关系。和第4章一样，用算法第一次发现奖励所需的周期数作为探索效率的衡量指标，通过实验得到了6个数据样本，显示在表2中，其中l表示算法第一次发现奖励所需的周期数量。为了表示出两者之间的关系，用多项式回归来拟合这6个点，表示如下：

其中，w1,w2,…,wm为m次多项式的参数，可以通过最小二乘法求出。测试了多个m值，发现当m为3时，均方误差最小，即两者之间的关系可以通过3次多项式来近似，如下：

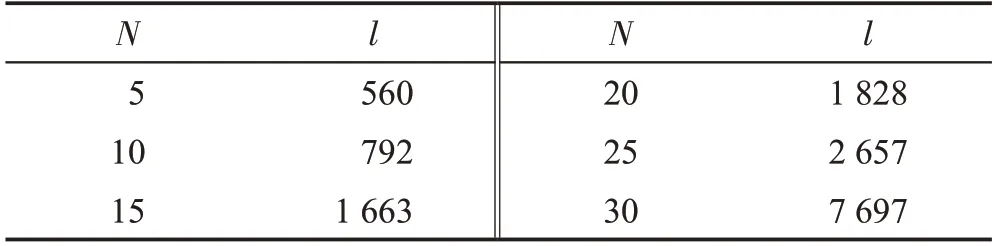
Table 2 The number of episodes required to find rewards表2 发现奖励所需的周期数

其中，参数保留小数点后两位。因此，BBDQN算法在面对深度探索问题时，算法的时间复杂度是多项式级别的，具体为O(N3)，优于随机探索策略ε-贪婪的时间复杂度O(2N)。

6.2 有关格子世界的进一步分析

在图3中DQN算法和Bootstrapped DQN算法比较起来没有明显的差别，但这并不代表两个算法的探索效率是一样的。事实上，Bootstrapped DQN算法的探索效率要比DQN更高。为了证明这一结论，进行了一系列实验。

在上一节提到了格子世界的规模表示为N×N，学习器的个数用K表示，比较了当K固定为10，N为{10，20，30}时各算法的性能。此外，又比较了当N固定为20时，K为{10，20，30}时各算法的性能。当格子世界的规模变小时，Bootstrapped DQN相较于DQN的优越性就体现出来了。如图4所示，当K为10且N为10时，DQN算法的遗憾一直增长，而Bootstrapped DQN和BBDQN在1 000个周期内就找到了最优策略。此外，当学习器的数量增大时，Bootstrapped DQN相较于DQN的优越性同样能体现出来。如图5所示，当K为30且N为20时，Bootstrapped DQN算法在2 000个周期左右的时间点找到最优策略。

Fig.4 Comparison of algorithm performance in Gridworld(N=10，K=10)图4 格子世界（N=10，K=10）上算法性能比较

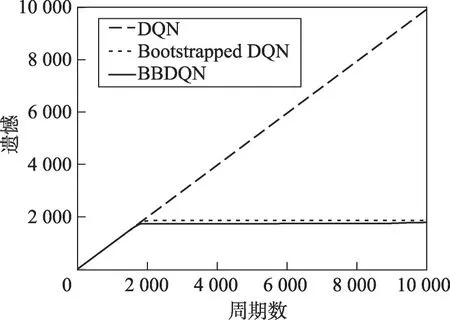
Fig.5 Comparison of algorithm performance in Gridworld(N=20，K=30)图5 格子世界（N=20，K=30）上算法性能比较

所有实验的结果显示在表3中，由于空间限制，Bootstrapped DQN在表中表示为BDQN。此外，6.1节的实验结果即表中K=10，N=20所示的结果。在表3中，能在10 000个周期内学习到最优策略的算法的遗憾用加粗字体显示，可以看到DQN在所有的实验设置中都没能在10 000个周期内找到最优策略，而Bootstrapped DQN只有当K=10、N=10（格子世界的规模减小）或K=30、N=20（学习器的数量增加）时，才能在10 000个周期内学习到最优策略，而BBDQN在所有设置下都能在10 000个周期内学习到最优策略。从表3中还可以看出，当格子世界的规模较小时（N=10），BBDQN算法和Bootstrapped DQN算法的性能相差不大，而且由于BBDQN加入了随机初始化的先验网络，BBDQN的性能甚至略低于Bootstrapped DQN，但是当格子世界的规模增加时，本文提出的BBDQN算法的优越性就愈发明显，这也是BBDQN更适合解决深度探索问题的体现；此外，BBDQN算法的性能并不会随着学习器的数量增加而增加，这就意味着BBDQN的空间需求低于Bootstrapped DQN，因为学习器的数量越多，就需要越多的空间来存储每个学习的参数，且这些算法都是使用神经网络作为函数逼近器，每个网络的参数都是百万级的，而BBDQN并不像Bootstrapped DQN一样要通过增加学习器的数量来提高算法性能（如表3所示），因此BBDQN的空间需求低于Bootstrapped DQN。

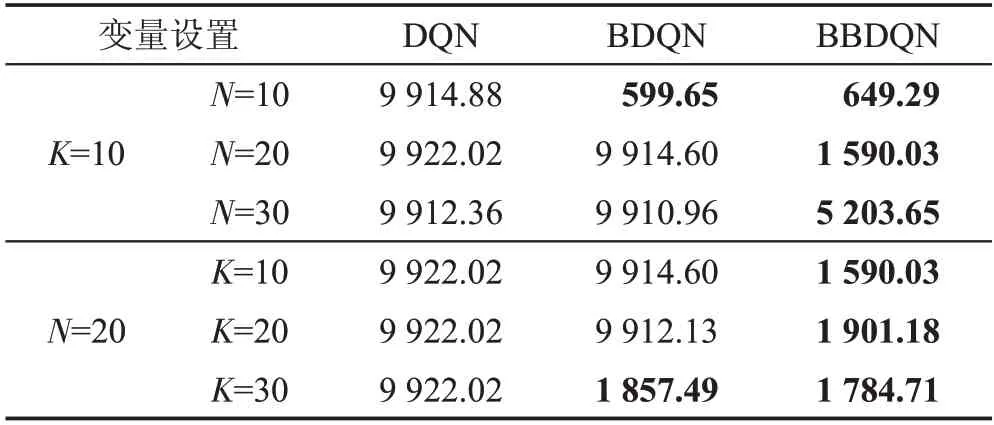
Table 3 Cumulative regret of each algorithm in 10 000 episodes表3 各算法在10 000个周期内累积的遗憾

6.3 Mountain Car的变体

Mountain Car问题如图6所示，在该问题中，小车的初始位置处于山底地区，目标是到达右边山顶，智能体接收到的状态信号是目前所处的位置以及小车的速度，智能体有3个可供选择的动作，分别是左加速、不加速以及右加速，小车的动态模型如下：

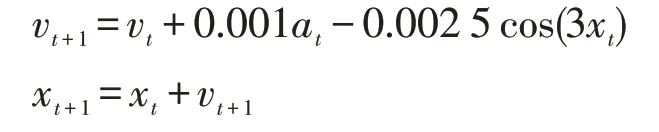
其中，x代表小车所处位置且有-1.2 ≤x≤0.6；v代表小车的速度且有-0.07 ≤v≤0.07；a代表智能体选择的动作，3个动作[左加速，不加速，右加速]对应的a值为[ 1,0,1]。当小车到达左端位置即x=-1.2时速度将重置为0，如果小车位置大于0.5（即到达目标区域）则该周期结束，进入下一周期，如果小车在200个时间步内还没有到达右边山顶，则强制结束该周期并进入下一周期。该问题的主要难点在于小车的动力无法抵消重力，因此无法直接通过右加速到达右边山顶，必须借助惯性才行。在原问题中，小车每一个时间步都获得-1的奖励，直到周期结束为止。

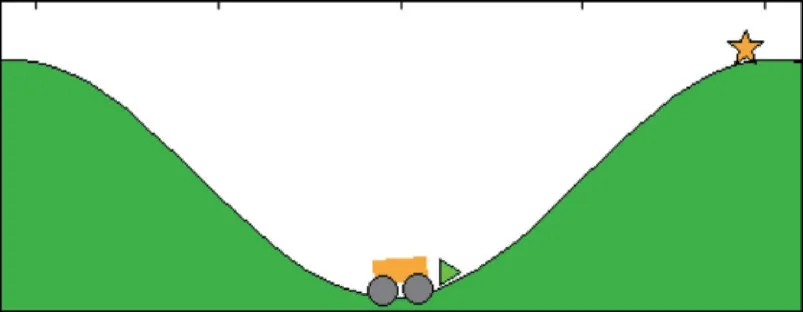
Fig.6 Mountain Car problem图6 Mountain Car问题

对原问题的奖励信号做出修改，使其与深度探索问题的结构相吻合。每当小车进行加速，无论是左加速还是右加速，都需要一定的代价，即接收到一个负的奖励信号，和格子世界一样，将其设置为-0.01/N，只不过这里的N是最优策略到达右边山顶所需的平均步数；如果不加速，则无需付出代价，即奖励为0；而一旦小车到达右边山顶将接受到+1的奖励。实验结果如图7所示，使用ε-贪婪探索的DQN算法其累积奖励一直小于0，代表该算法没有找到包含奖励的区域，而Bootstrapped DQN和BBDQN算法在200个周期内就发现了奖励区域。虽然Bootstrapped DQN一开始的累积奖励高于BBDQN，但在500个周期左右的时候BBDQN就超出Bootstrapped DQN了，而且增长的速度（曲线斜率）也明显快于Bootstrapped DQN。由于本文使用的BBDQN方法使用的先验网络的参数是随机初始化的，因此训练开始的时候BBDQN的累积奖励低只能说明随机初始化的先验网络的参数和正确的值网络的参数相差较远。

Fig.7 Comparison of algorithm performance on variant of Mountain Car图7 Mountain Car的变体上的算法性能比较

7 结束语

结合近几年兴起的深度学习技术可以提高传统强化学习算法的性能，然而这方面的进展仅对强化学习中的泛化有帮助。强化学习和监督学习最主要的区别就在于强化学习除了泛化外还存在两个问题：（1）平衡探索与利用之间的关系；（2）信用分配问题。本文主要解决的探索利用困境这一问题。结合贝叶斯方法可以提高强化学习算法的探索效率，几十年前就有人做过这方面的研究，然而之前的方法无法适用于神经网络这类非线性模型，本文的贡献就在于提出了一种能够通过数值计算得到神经网络参数后验分布的样本的方法，并将该计算方法和Bootstrapped DQN结合得到BBDQN算法。通过两个环境下的实验证明了BBDQN算法的探索效率优于使用ε-贪婪策略的DQN算法以及Bootstrapped DQN算法。

进一步研究的方向是：本文计算Q函数参数后验分布的样本的方法用于计算策略梯度（policy gradient）方法中策略函数πθ参数的后验分布的样本时，能否有效提高策略梯度方法面对深度探索问题时的探索效率。