基于局部模式的癫痫脑电信号自动分类方法

齐永锋,李陇强

(西北师范大学 计算机科学与工程学院,兰州 730070)

0 概述

癫痫是一种急性和复发性神经疾病,其主要临床症状表现为发作性抽搐和感觉、意识及精神障碍等,严重影响患者的日常生活和工作[1]。目前,对癫痫进行临床诊断的主要方法为CT扫描、磁共振波谱和脑电图(Electroencephalogram,EEG)分析。与前2种方法相比较,EEG分析不对人体造成损伤且成本较低,因而成为当前癫痫诊断的主流方法。癫痫诊断一般由医生通过对患者的EEG数据分析,然后根据自己的临床经验来给出结论。由于癫痫发作的不确定性、个体差异性、其他大脑疾病及不明原因引起的神经方面的异常,使得这种诊断方式容易造成误诊[2],因此通过计算机分析和自动识别癫痫脑电信号有着重要的现实意义。

文献[3]将人工神经网络应用到癫痫自动检测中,提出以“特征提取”结合“监督型分类器”的设计理念,成为之后癫痫自动检测的主要设计方法,而如何设计更优秀的特征提取方式和分类器则成为探究的热点。信号分析方法在特征提取方面起到了重要的作用,其应用在EEG信号分析中主要分为时域、频域、时频域和非线性动力学四大类。近年来,线性预测[4]、分数线性预测[5]、基于最小最大分类树的径向基函数神经网络[6]、小波变换[7-9]、经验模态分解(Empirical Mode Decomposition,EMD)[10-11]等技术在诊断癫痫EEG信号方面取得了较好的效果。文献[12]在假设EEG信号是静止信号的基础上,引入基于傅里叶变换(Fourier Transformation,FT)和决策树的混合框架,其中FT用于特征提取,决策树用于分类。文献[13]使用希尔伯特-黄变换(Hilbert-Huang Transform,HHT)结合支持向量机(Support Vector Machine,SVM)进行癫痫EEG信号分类,从得到的灰度子图像直方图中提取像素强度的均值、方差、偏度和峰度4个统计特征,其分类准确率能够达到99.125%。

基于局部模式变换的特征提取技术由于计算相对简单,被广泛用于不同的模式识别,例如将局部二进制模式(Local Binary Patterns,LBP)应用在人脸识别、语音处理等领域[14-15]。但是该算法对噪声比较敏感,中心点像素受到噪声污染后使得特征点发生变化,无法处理窗口的中心像素点与邻近像素点像素值相等的情况,导致提取的局部特征不完整,难以进一步挖掘信号中隐藏的细节信息。

针对上述问题,本文提出一种癫痫EEG信号的分类方法,通过设计的一维局部三值模式(1D Local Ternary Pattern,1D-LTP)算子,提取信号的局部三值特征,对其主成分分析(Principal Component Analysis,PCA)降维后用极限学习机(Extreme Learning Machine,ELM)进行分类。

1 癫痫EEG信号的分类方法

本文的癫痫EEG信号分类流程如图1所示。

图1 癫痫EEG信号分类框架

1.1 一维局部二值模式

LBP描述算子是一种简单但高效的纹理运算符,它将各个像素与其附近的像素进行比较,并把结果保存为二进制数,即当中心像素值小于等于邻域像素值时,该像素点的位置赋值为1,否则为0,最后形成二进制序列并进行编码,结果即为中心像素的LBP值[16],其计算过程如式(1)与式(2)所示。

(1)

(2)

其中,(xk,yk)是中心像素,fk是其灰度值,fi为相邻像素的灰度值。当邻域大小为3像素×3像素时,(M,L)取值为(8,1),n=9,即为8像素邻域,LBP 编码过程如图2所示。

图2 LBP算子示意图

1.2 一维局部三值模式算子

LBP具有旋转不变性和灰度不变性等优点,但对噪声比较敏感,并且算子本身不够完善,提取的局部特征不完整。为了降低对中心点像素值的依赖,减少噪声影响,提取更具鉴别性的特征,本文提出1D-LTP算子。该算子也是局部纹理描述算法,但较LBP更具判别性并且受到统一区域的噪声影响更小。1D-LTP通过计算顶层模式及底层模式的二值编码转换为二值模式。本文运用此方法将信号特征值扩大一倍,最后进行合并,大幅减小了噪声及个别值的影响,其计算过程如下所示。

(3)

其中,nS表示信号点S在信号段n中的位置。

计算选取信号段的均值M及标准差ρ,对于每个信号点S,求其与选取信号段的均值的差值,差值计算如式(4)所示。

di=S-M

(4)

根据式(5)计算信号点S的1D-LTP变换码。

(5)

(6)

1D-LTP算子涉及的各个步骤如图3所示。

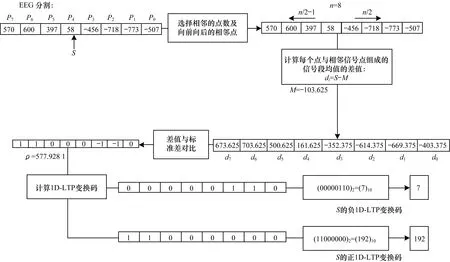
图3 信号点S的1D-LTP变换码

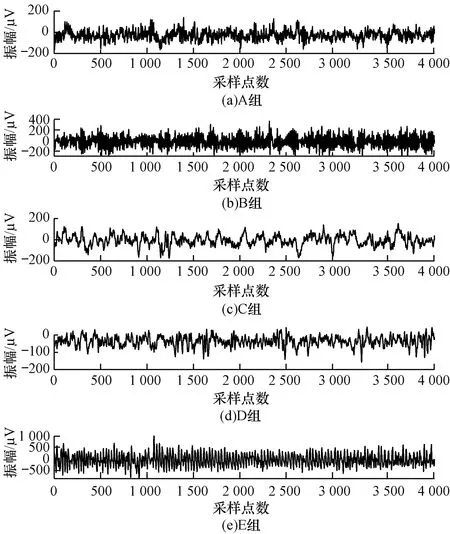
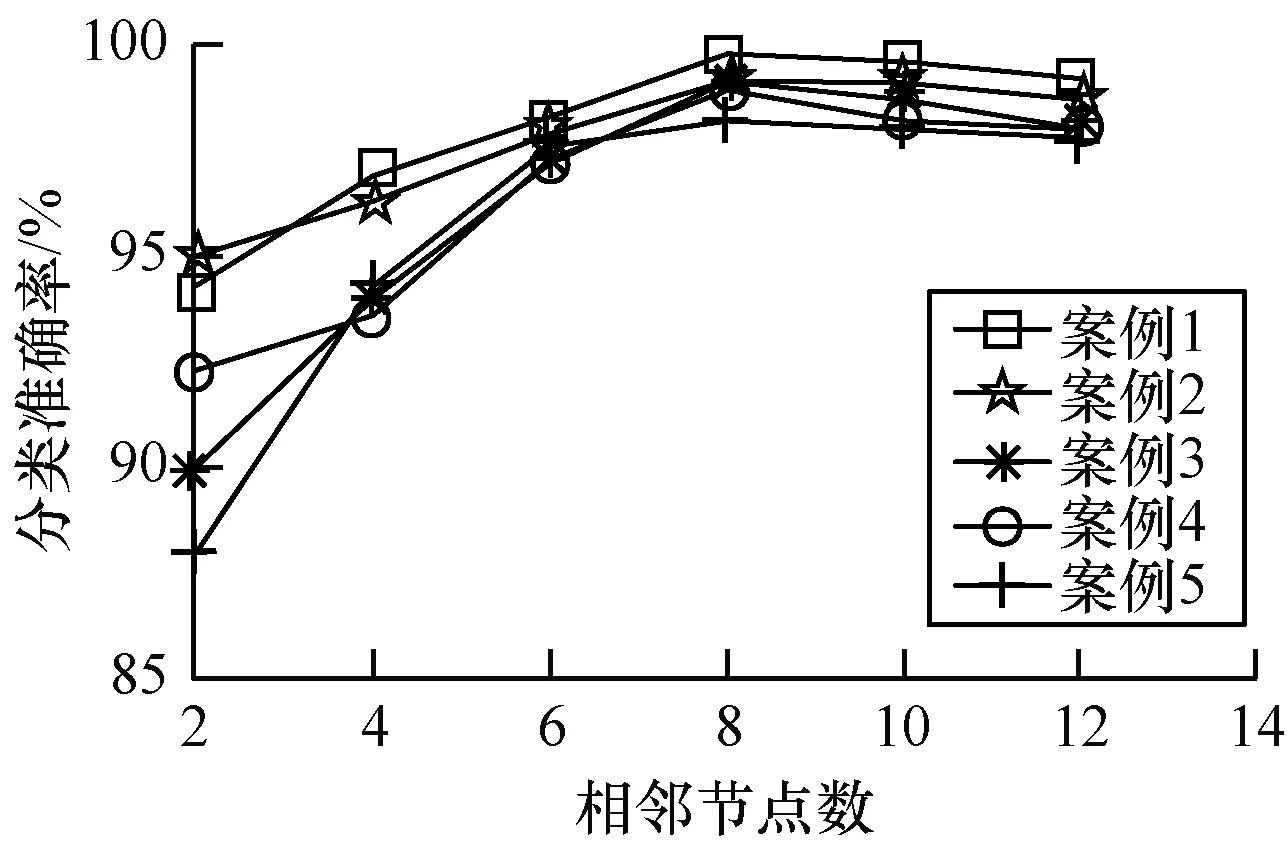
1D-LTP算子的时间复杂度计算如下:设M是由k个点组成的信号,每个信号点考虑相邻点组成的信号长度n(n

1.3 基于直方图的特征向量

每个变换代码表示信号的局部模式结构,本文将其转换为变换代码直方图。直方图以图形方式总结了二维空间中的结构分布,其中横轴包含变换代码的范围,纵轴包含每个代码的频率(出现次数)。本文以图形结构表示特征向量并用于分类,实验中不同组基于1D-LTP算子获得的一小段特征直方图如图4所示。

图4 1D-LTP特征直方图

1.4 特征降维及分类

本文将直方图表示对应的EEG信号的特征向量经PCA降维后输入到ELM分类器中。为避免分类结果受随机性的影响,在进行分类时,随机选择90%的特征值作为训练集,剩余的10%用作测试集。本文以正常和癫痫发作间期的EEG为负类,发作期EEG为正类,使用ELM进行分类的步骤如下:

步骤1采用PCA对提取的特征进行降维。

步骤2随机选取降维样本的10%构成测试样本集,其余样本组成训练样本集,计算测试精度。

步骤3随机选取降维样本的另外10%构成测试样本集,其余的样本组成训练样本集,计算测试精度。

步骤4重复步骤3,直至遍历每个样本。

其中,随机化处理是为了使训练样本集更具代表性,不会对最终测试结果造成影响。

2 实验与结果分析

本文实验数据来自于德国波恩大学脑电图数据库,数据集详细描述见文献[17]。基准数据集由5个组(A、B、C、D和E)组成,每组有100个单通道EEG信号,记录每个EEG信号23.6 s,含有4 097个采样点,采样频率为173.6 Hz。A组是5名健康自愿者在睁眼状态下采集的脑电数据集,B组是5名健康自愿者在闭眼状态下采集的脑电数据集,C组是5名癫痫病患者在癫痫发作间期在致痫灶对侧域采集的脑电数据集,D组是5名癫痫病患者在癫痫发作间期在致痫灶内域采集的脑电数据集,E组是5名癫痫病患者在癫痫发作期在致痫灶内域采集的脑电数据集[17]。各个类别的EEG信号如图5所示。

图5 癫痫EEG信号

本文计算每个信号点的特征变换码以直方图的形式排列,并对所有信号重复该过程。不同组基于1D-LTP特征变换码的直方图如图6所示。

图6 EEG信号的1D-LTP特征直方图

本文采用了敏感度、特异性和准确率[18]对分类性能进行评价,三者计算方法如下:

(7)

(8)

(9)

其中,TP为正样例中正确归类的数目,TN为负样例中正确归类的数目,FP为负样例中错误归类的数目,FN为正样例中错误归类的数目用来表示分类错误。

本文实验案例均是处理二进制分类的问题,具体案例如下:

案例1A组和E组混合数据。

案例2B组和E组混合数据。

案例3C组和E组混合数据。

案例4D组和E组混合数据。

案例55组混合数据。

使用本文方法获得的灵敏度、特异性和准确率如表1所示。

表1 本文方法各案例分类结果

Table 1 Classification results of each case using the proposed method

案例灵敏度/%特异性/%准确率/%案例199.8799.7199.79案例299.2499.0699.15案例398.9599.3199.13案例499.1498.7298.93案例598.0598.3098.20

从表1可以看出,1D-LTP算子对5个案例的分类准确率均较高,分别为99.79%、99.15%、99.13%、98.93%以及98.20%，这说明本文方法合理有效。

在本文方法中,特征向量的长度l取决于在评估变换代码时考虑的相邻点n的数量,其关系为:

l=2n

(10)

本文实验验证了不同相邻点数量对分类准确率的影响,结果如图7所示。从图7可以看出,当相邻点的数量n=8时,特征向量的长度为256,分类准确率最高。

图7 不同数量相邻点的1D-LTP性能

Fig.7 1D-LTP performance of different numbers of adjacent points

在n=8的情况下,将本文方法与其他方法对癫痫EEG信号的识别准确率进行比较,结果如表2所示。其中,对比方法均采用10折交叉进行评估。从表2可以看出,本文方法能够实现高精度分类。

表2 不同分类方法准确率对比

Table 2 Accuracy comparison of different classification methods

案例方法 分类准确率/%案例1DTCWT+CVANN[19]100.00加权排列熵+SVM[20]99.50HHT+SVM[13]99.13小波变换+ANN[21]96.00本文方法99.79案例2LNDP+ANN[22]99.25加权排列熵+SVM[20]85.00置换熵+SVM[23]82.88本文方法99.15案例31D-LGP+ANN[22]99.10加权排列熵+SVM[20]93.50模糊近似熵+SVM[24]99.60置换熵+SVM[23]88.00本文方法99.13案例41D-LGP+ANN[22]99.07加权排列熵+SVM[20]96.50模糊近似熵+SVM[24]95.85本文方法98.93案例5DTCWT+CVANN[19]99.15模糊近似熵+SVM[24]97.38本文方法98.20

3 结束语

本文提出一维局部三值模式算子1D-LTP,并将其应用于癫痫脑电信号的分类。相对于LBP算子,该算子能较好地反映数据间的相关性,得到的脑电特征具有良好的鉴别性,且对噪声不敏感,在一定程度上减少了噪音影响及特征丢失的情况。在波恩大学癫痫病研究中心数据库上的实验结果表明,本文方法能够对癫痫脑电信号进行准确区分,分类准确率可达99.79%,为快速准确地自动诊断癫痫疾病提供了一个解决方案。