基于多层水平集函数的三维多相图像分割
2020-02-19潘振宽魏伟波王加忠
徐 娟,潘振宽,魏伟波,王加忠
(青岛大学 计算机科学技术学院,山东 青岛 266071)
0 概述
多相图像分割是图像处理、图像分析、计算机视觉等领域中的研究热点之一,而三维多相图像分割则是其中的重点和难点。三维多相图像分割在模式识别、医学诊断、地球物理勘探、三维图像重建等方面具有重要的应用价值[1-2]。
在图像分割领域中,人们提出许多关于分割问题的模型。CHAN和VESE将分段常值Mumford-Shah模型[3-4]简化,结合水平集方法[5-6]建立了基于区域的分段常值两相图像分割模型,即Chan-Vese模型[7-8]。随后,VESE和CHAN又提出了用n个水平集函数划分2n个区域的区域竞争策略,进一步将该模型扩展为分段常值和分段光滑的多相图像分割模型,即多相图像分割Chan-Vese模型[9-10]。随着水平集个数增加,目标区域的表达及其对应的能量泛函求解方程越来越复杂,为此,文献[11]根据划分区域的编号与其二进制表达的关系建立每个区域的特征函数的通用表达式。文献[12]采用文献[13]提出的区域划分方案,用n个连续水平集函数的零水平集建立了n相图像分割的变分水平集方法。文献[14]用n个离散常值的水平集函数,结合拉格朗日多项式差值,建立了分段常值多相图像分割的变分模型。文献[15]提出一种新的区域划分方法,该方法采用几何的方式引入n个水平集来划分n+1个区域。但上述模型都存在以下不足:均需对多个函数求极值,计算效率不高;随着水平集个数增加,目标区域的表达及对应的能量泛函求解方程越来越复杂。此外,多相水平集模型难以确定用于多相分割的水平集函数的个数。针对上述问题,文献[16]基于Chan-Vese多相图像分割模型的区域表达策略,提出了用一个连续变化的水平集函数建立表达n相变分形式的分层水平集Chung-Vese模型,采用最少的水平集函数来表达多个相,无需增加约束条件,避免了重叠和漏分现象。但该模型只提供了一个区域分割方案,没有给出通用区域分割的公式表达,当相数较多时将导致能量泛函和相关水平集函数演化方程表达复杂,为此,文献[17]对Chung-Vese模型提出区域标记的统一化表达。多层水平集Chung-Vese变分模型在二维多相图像分割中得到充分的研究和应用[18],但是如何将其应用到三维多相图像分割中,还未见相关研究报导。
文献[13]提出的变分水平集方法将变分法和水平集方法相结合,由于其具有自适应复杂拓扑结构变化、二维和三维图像分割模型表达一致、数值计算方法稳定以及具有集成多模型信息能力等特点,已被广泛用于图像分割的研究领域中[19]。但变分水平集方法存在计算效率低等问题,为此,文献[20]将分裂算法与Bregman迭代[21]相结合,通过引入辅助变量和迭代乘子,提出了快速Split-Bregman方法。该方法具有较高的计算效率和迭代精度。
文献[13]设计了一个函数在多层水平集标记的模型实现对图像不同区域的分割,但只验证了该模型对二维图像的分割效果,并未指出其对三维图像是否具有同样的通用性和实用性。由于一个Lipschitz连续多层水平集函数能有效地对两相和多相三维图像分割,本文将文献[13]的二维图像分割模型向三维图像进行扩展,设计满足图像不同区域互不重叠、划分方案对称、符合唯一划分条件的特征函数,在变分水平集理论框架下基于分段常值假设建立统一的三维图像的两相和多相变分模型,并采用Split-Bregman投影方法[22]对模型求解,即在Split-Bregman方法基础上引入投影变量,将约束转化为解析投影公式进行求解。
1 多层水平集函数的变分方法
多相图像分割是按照一定的区域划分方案将图像分割成多个相的过程,一个有效的多相图像分割模型需要解决的问题包括能量泛函的表达、多相区域的划分策略以及演化方程的数值计算等,其中,区域划分方案的选择和区域特征函数的设计是多相图像分割的核心。为防止区域之间的重叠和漏分,多相图像分割必须解决好区域之间的竞争策略。下文将介绍本文区域划分方案对应的区域特征函数表达和多层水平集函数的变分方法。
1.1 变分水平集方法
水平集方法[7]是一种有效的演化曲线/曲面隐式表示,即将分割边界/表面隐式表示为在欧拉框架中演化的更高维函数的水平集,该高维函数即水平集函数。水平集方法自动处理拓扑变化,为分割准则的设计提供了很大的灵活性,以适应对图像及其结构的各种假设[23],包括不同的外观模型[23-25]和形状先验[26]。水平集方法对二维和三维甚至更高维图像分割具有相同的表达形式。因此,在三维图像分割研究中,二维图像分割的能量模型以及区域划分方法依然适用。
变分水平集方法是文献[13]针对闭合曲线C演化的能量泛函E(C)最小化问题提出的一种新的水平集方法,通过引入嵌入函数φ(x)和Heaviside函数,将E(C)改造成E(φ(x)),再利用变分法求得关于φ(x)的偏微分方程[27],其中要求保证水平集函数在演化过程中始终保持符号距离函数的特征|φ|=1。C={(x)|φ(x)=c0},C是满足函数φ(x)等于常值c0的点集,称为函数φ(x)的一个水平集。函数φ(x)为曲线C的嵌入函数,称为水平集函数。当常数c0=0时,C={(x)|φ(x)=0}被称为水平集函数φ(x)的零水平集,如图1所示。本文基于多层水平集函数的n层水平集在图像中的曲面演化对图像进行分割,需要通过变分水平集方法解决曲面演化的能量泛函的极值问题。
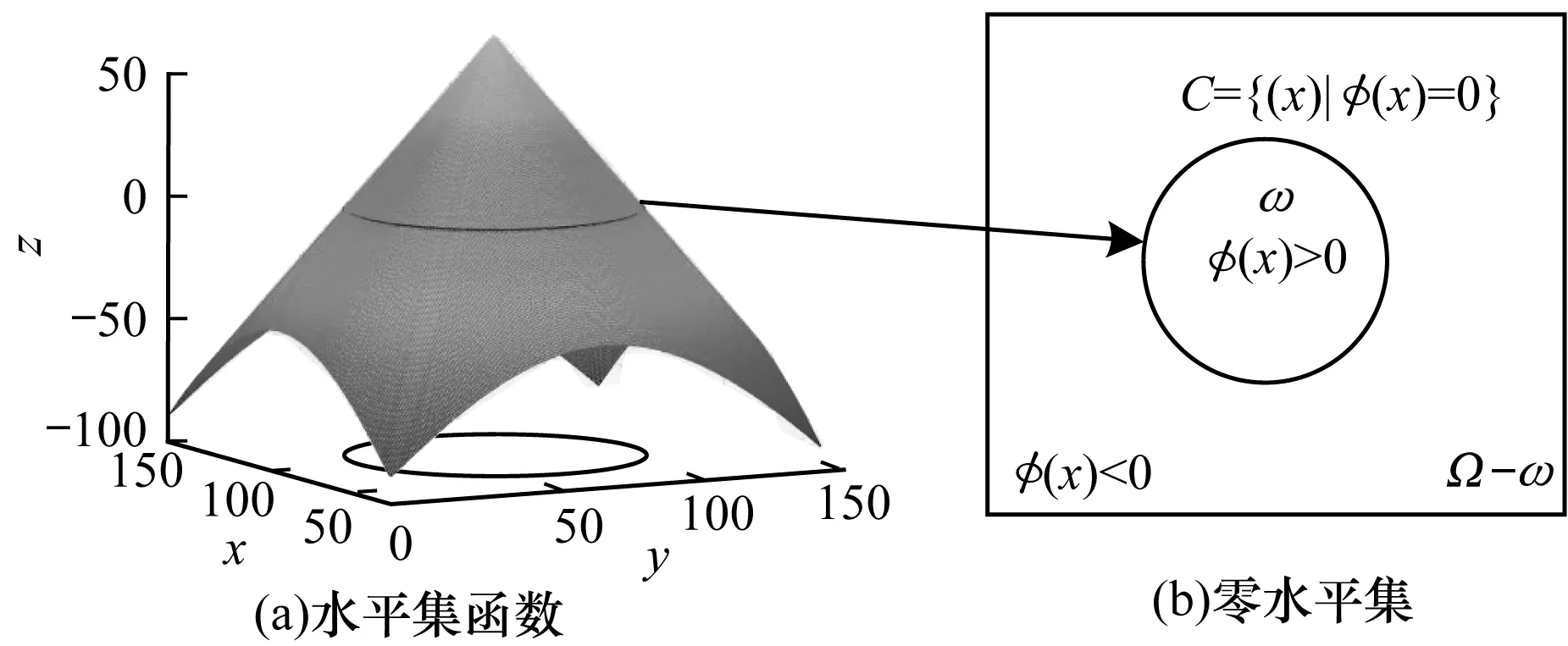
图1 水平集函数和零水平集对应的轮廓线
1.2 多层水平集方法
多层水平集模型[14]在Chan-Vese模型基础上引入外延生长岛动力学,利用水平集函数的多层等高线的曲线演化来完成图像分割,得到改进的水平集图像分割算法模型,以处理多相图像分割问题。该模型也被称为Chung-Vese模型,比多相水平集模型简单,运算速度快。多层水平集函数的2层嵌套水平集示意图如图2所示。
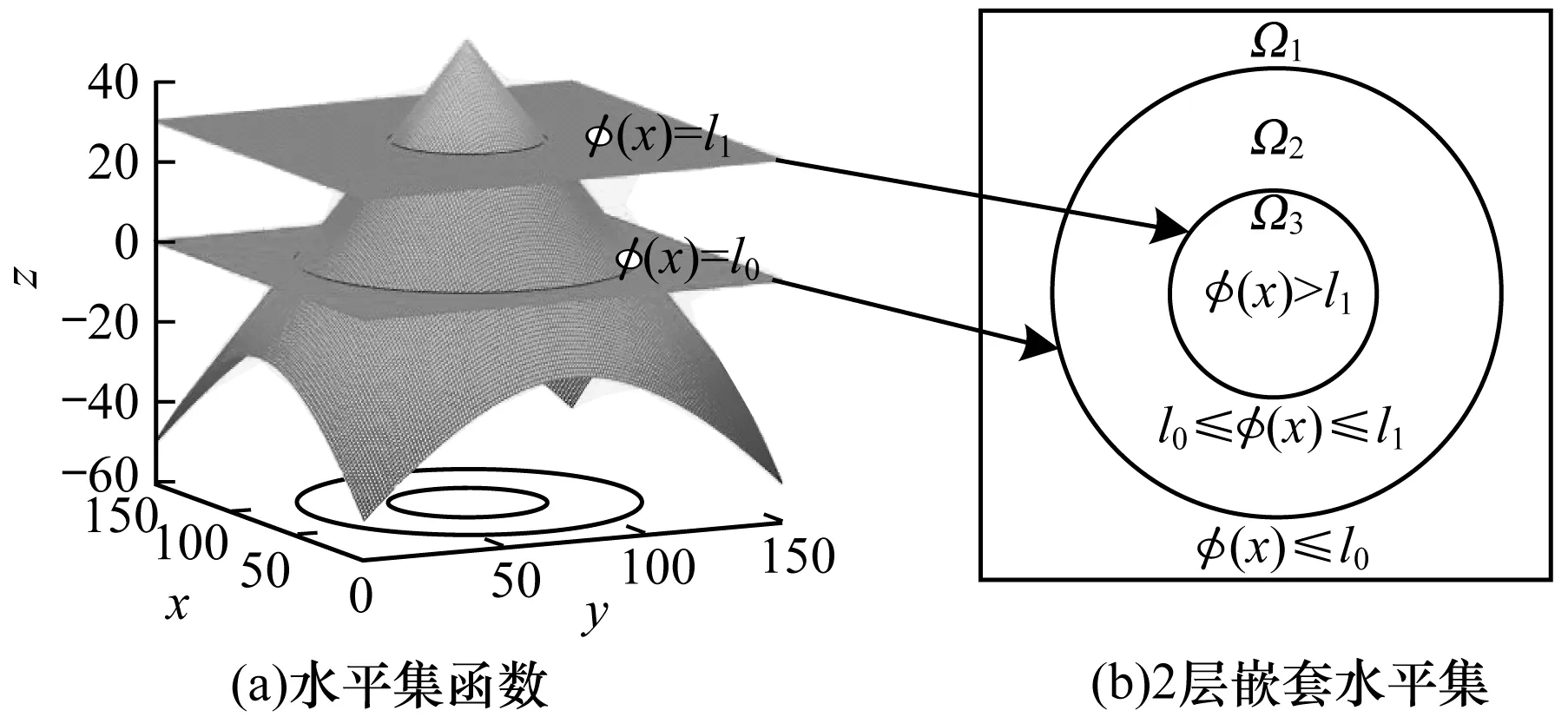
图2 多层水平集函数的2层嵌套水平集示意图
1.3 多层水平集模型的区域划分方案

Ω1:χ1(φ)=H(φ-l0)(1-H(φ-l1)),l0≤φ(x)≤l1
Ω2:χ2(φ)=H(φ-l1)(1-H(φ-l2)),l1<φ(x)≤l2
⋮
Ωn:χn(φ)=H(φ-ln-1)(1-H(φ-ln)),ln-1<φ(x)≤ln
(1)
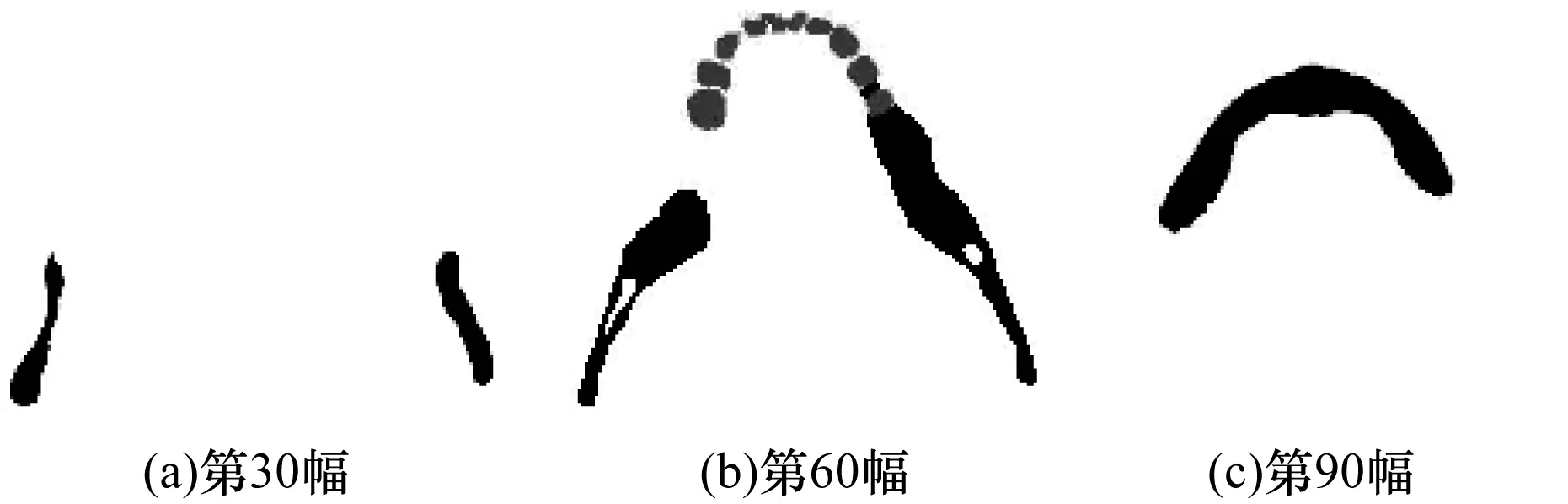
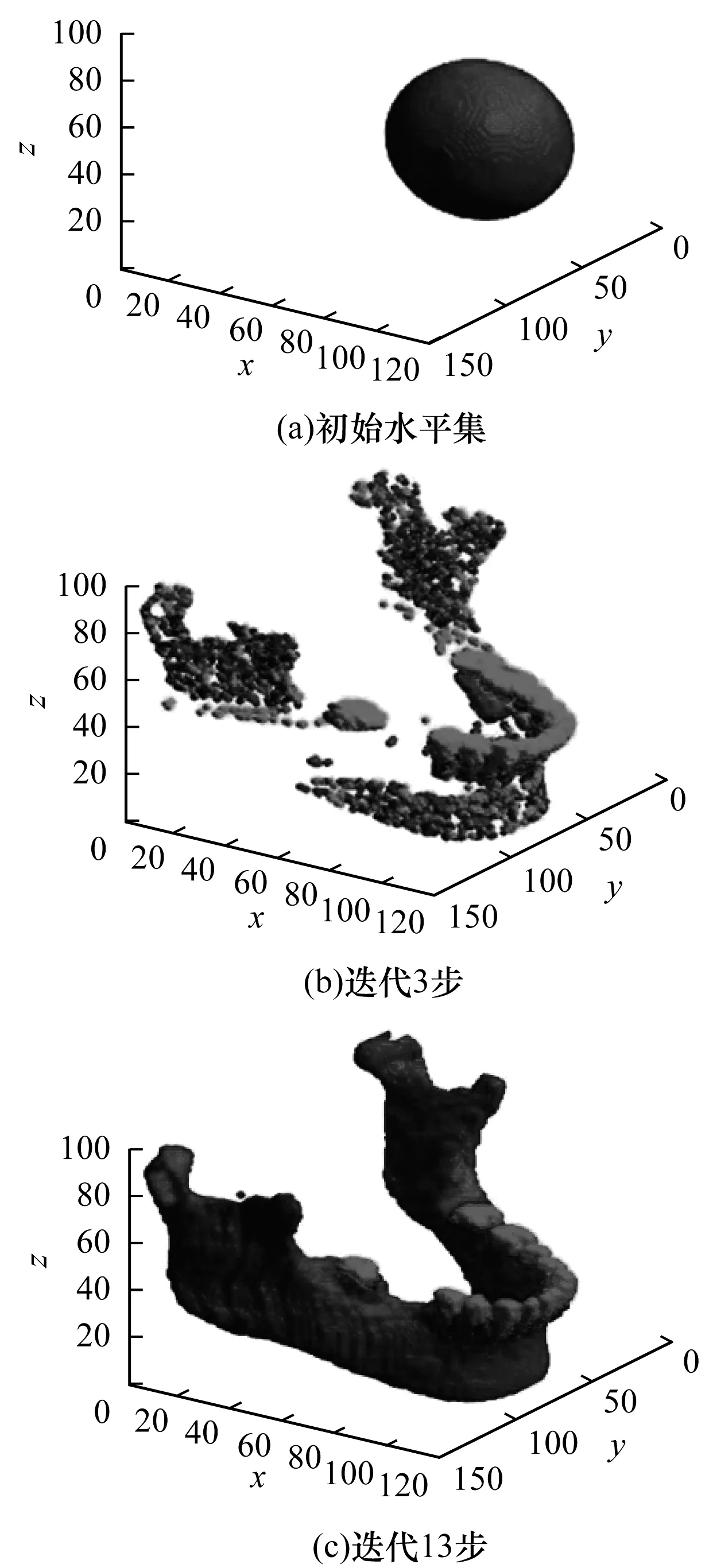
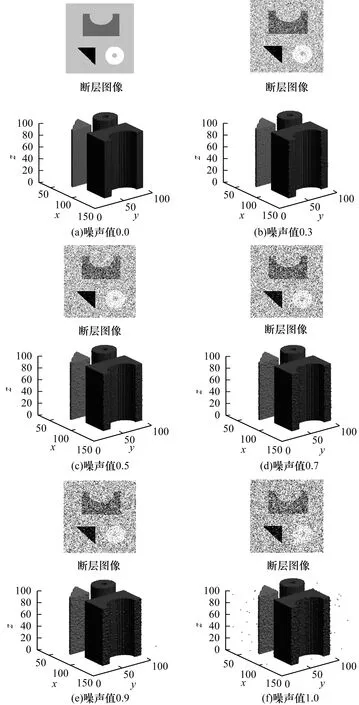
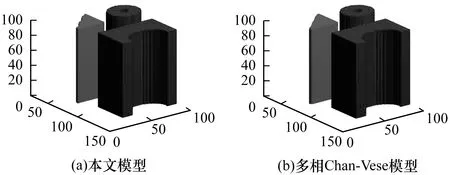
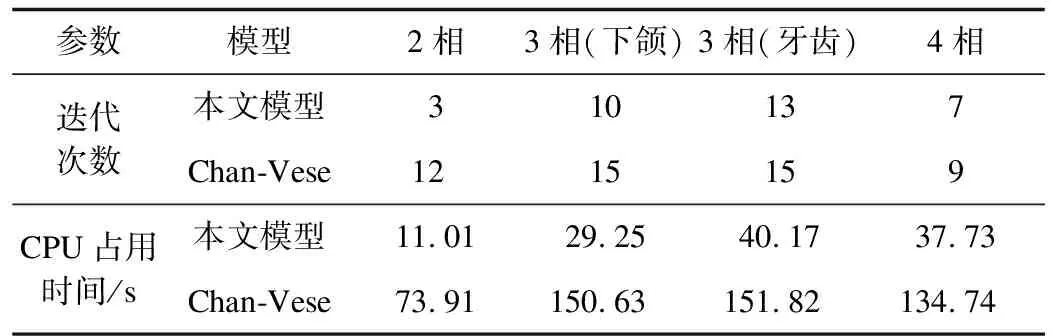
由φ(x)∈[l0,ln](0=l0 x∈Ωi:li-1<φ(x)≤li φ-l0>0,φ-li≤0 φ-l1>0,φ-li+1≤0 ⋮ ⋮ φ-li-1>0,φ-ln≤0 (2) 当χi(x)=1时,有: χ1(x)=0,χ2(x)=0,…,χi-1(x)=0 χi+1(x)=0,χi+2(x)=0,…,χn(x)=0 (3) 即: (4) 设f为三维图像的图像强度,多相图像分割变分水平集模型通过引入1个包含n个不同水平集(0=l0 (5) 满足约束条件: (6) 以保证水平集函数在演化过程中始终保持符号距离函数的特征。ui=(u1,u2,…,un)为f在区域Ω中的分段常值,其估计式为: (7) 本文采用规整化的Heaviside函数和Dirac函数[28]实现区域划分的函数表达,即当ε→0时,Hε(φ)→H(φ)(ε趋于0时,Hε(φ)近似Heaviside函数H(φ)),其表达式为: (8) (9) 其中,ε为数值较小的正数,为书写简洁,本文仍使用原符号表达。所以,边缘项可以等价表示为: (10) 因此,多层水平集图像分割模型的能量泛函可以等价表示为: (11) 本文采用高效、稳定的Split-Bregman投影方法对能量泛函求解极值。引入辅助变量w和Bregman迭代参数b,将式(11)转变为如下变分模型迭代格式: (12) s.t.|w|=1 (13) 其中,w0=0,b0=0,θ(θ>0)为惩罚参数。采用交替优化方法分别得到关于φ的欧拉拉格朗日方程及关于w的广义软阈值公式如式(14)和式(15)所示。 (14) (15) 其中: (16) (17) 为满足约束φ(x)∈[l0,ln],对函数φ(x)添加一个约束项为: φk+1=min(max(l0,φk+1),ln) (18) (19) 更新b得: bk+1=bk+φk+1-wk+1 (20) 本文算法步骤如下: 步骤1初始化φ0为水平集函数,w0=b0=0,k=0。 步骤2估计ui,i=1,2,…,n。 步骤3依次求解式(14)、式(15)、式(19)得到φk+1,wk+1。 步骤4更新bk+1=bk+φk+1-wk+1。 本文实验PC机的配置为:操作系统Win7 x64,处理器Intel(R)Core(TM)i5-4590 CPU @ 3.30 GHz,RAM 4.00 GB,编程运行环境MATLAB R2018b。三维图像共有3个维度,常见的三维图像有真实人体CT扫描图像和人工合成的三维图像。本文实验参数设置为空间步长h=1,时间步长Δt=0.1。 在图像分割模型中,2相图像分割是多相图像分割的一种特殊情况。本实验取真实人体牙齿周边部位CT扫描图像序列,图像规格为150×128×105。在实验中,将原本彩色图像预处理为灰度图像,将原本的灰色背景处理为白色以实现2相图像分割,其中,牙齿和下颌骨整体作为分割目标。预处理后的牙齿图像序列的3个断层图像如图3所示。该实验采用一个水平集函数的2个水平集l1=1和l2=3,相关参数ε=8,α=1,γ=1,θ=1.5,分割过程如图4所示。 图3 2相牙齿图像序列的断层图像 图4 2相图像序列分割过程 本实验使用规格为158×128×99的真实人体下颌部位CT扫描图像序列和128×128×105的牙齿部位CT扫描图像序列。该实验采用一个水平集函数的3个水平集l1=1、l2=3和l3=7,相关参数ε=8,α=1,γ=0.09×2552,θ=0.3。下颌部位和牙齿部位的图像序列中3个断层图像分别如图5和图6所示,其分割过程如图7和图8所示。 图5 下颌图像序列的断层图像 图6 牙齿图像序列的断层图像 图7 3相下颌图像序列分割过程 图8 3相牙齿图像序列分割过程 本实验使用人工合成的三维立体几何图像序列,图像规格为l1=1,l2=3,l3=7。该实验采用一个水平集函数的4个水平集l1=1,l2=3,l3=7和l4=15,相关参数ε=8,α=1,γ=0.01×2552,θ=0.08。几何立体图像序列中3个断层图像如图9所示,其分割过程如图10所示。 图9 立体几何图像序列的断层图像 图10 4相图像序列分割过程 不同类型的图像符合不同的概率分布,限于篇幅,本文仅给出Gauss噪声对4相立体几何图像序列分割效果的影响。图11为立体几何图像序列随机加入噪声值分别为0.0、0.3、0.5、0.7、0.9和1.0后相对应的分割结果,从图中可以看出,当噪声值小于1时,噪声对区域划分影响不大,但是会影响图像的分割效果,导致分割后图像表面不光滑。 图11 随机加入不同噪声值后对应的分割结果 多相图像分割Chan-Vese模型(以下简称多相Chan-Vese模型)划分n个区域需要引入lbn个水平集函数。除本文模型以外,该模型是在表达多个相时使用的水平集函数个数最少的多相图像分割模型,因此,本文将其选为对比模型。图12~图15依次为2相、3相(下颌)、3相(牙齿)及4相图像序列分别采用本文模型和多相Chan-Vese模型最终三维分割效果的主观对比。表1为2相、3相(下颌)、3相(牙齿)及4相图像序列分别采用本文模型和多相Chan-Vese模型最终三维分割效果的客观对比。 图12 本文模型和多相Chan-Vese 模型的2相图像分割效果对比 图13 本文模型和多相Chan-Vese 模型的3相牙齿图像分割效果对比 Fig.13 Effect comparison of three-phase tooth image segmentation between the proposed model and the multiphase Chan-Vese model 图14 本文模型和多相Chan-Vese模型的3相下颌图像分割效果对比 Fig.14 Effect comparison of three-phase mandibular image segmentation between the proposed model and the multiphase Chan-Vese model 图15 本文模型和多相Chan-Vese模型的4相图像分割效果对比 表1 本文模型与多相Chan-Vese模型的实验数据比较 从以上实验结果可以看出,本文模型可以有效地实现三维多相图像分割,并且迭代步数较少,分割速度较快。 本文针对三维多相图像分割提出一种新的变分水平集模型。利用基于一个连续水平集函数的多层水平集对图像进行区域划分,采用Split-Bregman方法实现三维多相图像分割。本文使用真实人体牙齿和下颌部位的CT扫描图像序列进行实验,结果表明,该模型能有效地分割图像。本文模型具有一定的实际应用价值,例如医生可以通过分割后重建的三维图像看见病人牙齿的缺损情况。但本文实验未对包含噪声的原始数据进行预处理,导致分割得到的图像不光滑,后续将对此改进,提高分割图像的光滑度。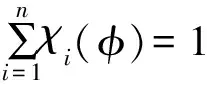
2 多层水平集的Split-Bregman投影方法
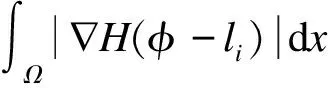

3 实验与结果分析
3.1 三维图像2相分割与重建

3.2 三维图像3相分割与重建



3.3 三维图像4相分割与重建


3.4 噪声对本文模型分割效果的影响
3.5 与多相图像分割Chan-Vese模型效果的对比



4 结束语
