大尺度展向波形圆柱绕流流场结构的数值研究
2020-02-19王汉林陈二云杨爱玲孙贵洋
王汉林,陈二云,杨爱玲,孙贵洋
(上海理工大学 能源与动力工程学院/上海市动力工程多相流动与传热重点实验室,上海 200093)
钝体绕流存在于许多工程实际中。周期性的涡脱落与柱体表面相互作用,形成周期性的表面载荷,引起结构振动乃至被破坏。因此,控制钝体绕流尾迹中的漩涡脱落,进而实现减振减阻特性的研究具有重要的理论意义和工程应用价值。
钝体绕流产生的自由剪切层对尾迹漩涡结构有直接的影响,同时也决定了钝体的受力特性。目前研究工作主要集中在基于通过改变钝体外形,从而影响柱体绕流的自由剪切层,进一步控制钝体绕流漩涡结构的基本思路,研究不同波形圆柱绕流的流场结构特性。例如,Lam 等[1-3]对波形圆柱的绕流特性进行了数值研究,获得了波形参数与阻力和漩涡长度的关系,并提出波形圆柱可以减阻18%,还讨论了波形圆柱绕流的抑振效果,通过改变表面几何参数来控制漩涡的脱落,抑制流激振动。这些数值研究工作均被后来的实验所证实[4-5]。
Zhang 等[6]应用流动图像显示技术研究了雷诺数为3 000 时波形圆柱的尾流涡结构,发现沿波形圆柱展向,流向漩涡正负交替排列。Lin 等[7]在研究大尺度波长圆柱绕流的流场结构时发现,不同大尺度波长下存在的最优波长比,可使减阻效果达到最大。对于大雷诺数,Ahmed 等[8]在雷诺数Re为20 000 时,对一系列波幅的波形圆柱在不同截面处的表面压力分布进行了实验研究,结果显示最大截面处的阻力系数要大于最小截面处。他们进一步研究了湍流下波形圆柱的尾流特性,然而并没有讨论该波形圆柱的减阻抑振情况[9]。Lee 等[10]使用热线仪和流动显示技术,在Re为5 300~50 000 范围内研究了不同波长波形圆柱绕流的减阻效果。
上述研究工作有助于深入理解波形圆柱绕流的减阻特性,但有关不同振幅波形圆柱绕流减阻特性的研究较少。本文主要目的是研究波形圆柱振幅对绕流减阻特性和尾迹流场特性的影响,以获得波形参数与气动和流场结构的关联规律。Re为3 000 时圆柱所引起的湍流绕流问题是典型的亚临界雷诺数问题,因此Re为3 000 时的圆柱绕流成为亚临界圆柱绕流的一个典型算例,其实验数据较丰富,所以本文采用的Re为3 000。
1 数值模拟
1.1 数学模型
本文采用大涡模拟(LES)方法获得圆柱绕流的流场解,其基本思想是通过滤波方法将湍流中的瞬时脉动运动分解为大尺度和小尺度两部分。大尺度运动通过求解可解尺度的N-S 方程直接得到,小尺度运动对大尺度运动的作用通过亚格子尺度模型来模拟。控制方程为[11]

τij为亚格子应力张量,定义为

本文采用经典的Smagorinsky 模型,它考虑到亚格子应力 τij与最大尺度应变张量成正比。
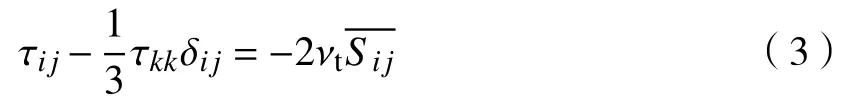
式中: δij为 克罗内克符号;Sij为滤波后的剪切应力张量; νt为湍流黏度。

式中:V为单元体积;Cs为Smagorinsky 常数。
1.2 计算模型及网格
图1 为本文圆柱绕流的计算域尺寸,在笛卡尔坐标系下表示,其中Dm为圆柱平均直径。选取圆柱底部中心为坐标原点,x方向与来流方向一致,y方向平行于圆柱横截面,沿圆柱方向取为z方向。上游断面距离圆柱中心为 8Dm,上、下面距离圆柱分别为 8Dm,下游断面距离圆柱中心1 6Dm,圆柱长为b。根据Lam 等[2]的数值实验研究,对于波长 λ较大的波形圆柱,为了减少网格量,节省计算时间,当b=λ时,能很好地体现波形圆柱的流动状况,所以本文展向高度选为λ。
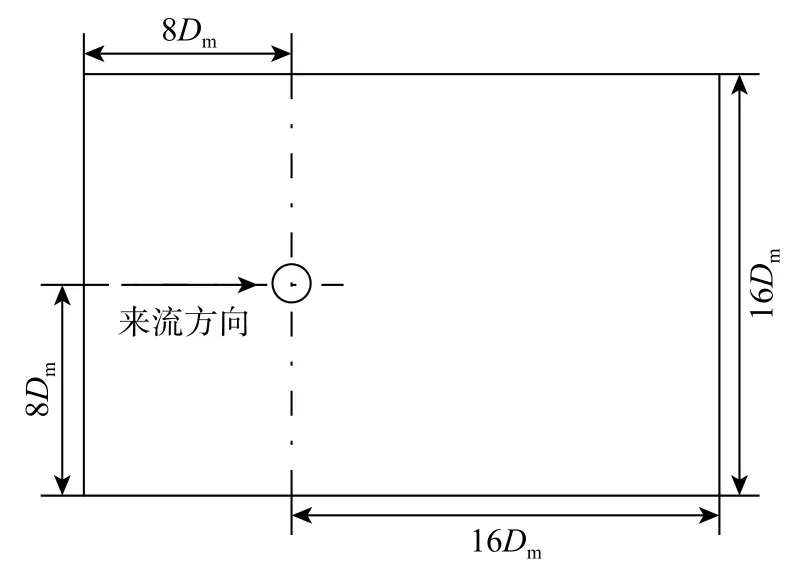
图 1 计算域尺寸Fig. 1 Size of the computational domain
图2 为波形圆柱示意图。波形圆柱是指将直圆柱的横截面直径延展向正弦变化得到的圆柱体,其变化参数为:Dz=Dm+2acos(2πz/λ),Dm=(Dmin+Dmax)/2, 其中:Dz为展向圆柱横截面直径;a为 振幅;x、y、z分别为顺流向、横流向、展向。
本文网格采用六面体结构网格,如图3(a)、(b)所示,近壁面第一层网格高度为0.01 mm,增长比为1.05,保证y+≤1,保证大涡模拟计算准确性。波形圆柱网格总数为650 万~680 万。
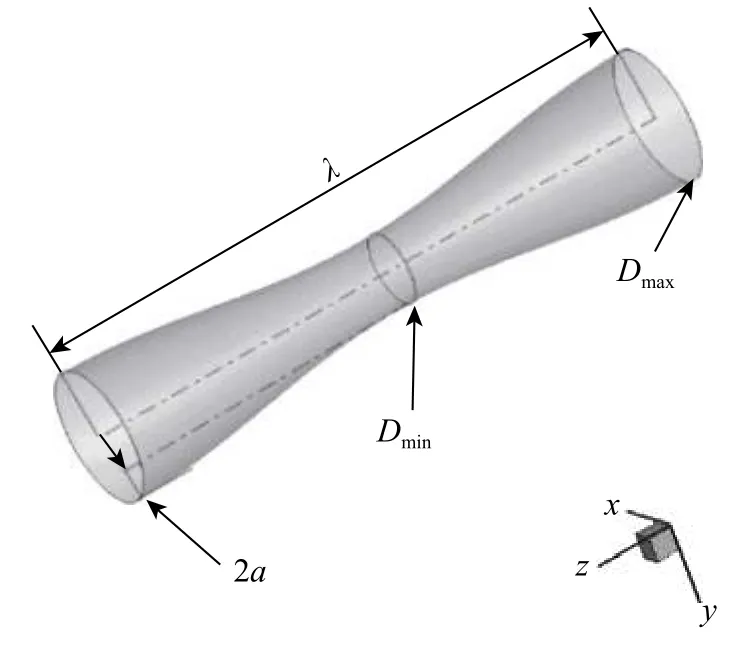
图 2 波形圆柱示意图Fig. 2 Schematic diagram of wave cylinder
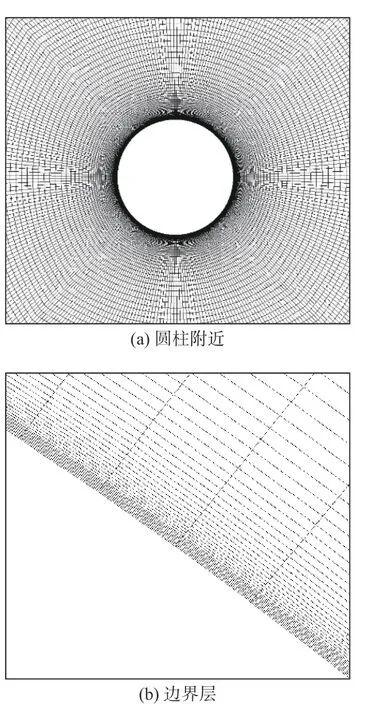
图 3 局部网格Fig. 3 Local mesh
1.3 边界条件
计算域入口设置及左、右面为速度入口,设定常流速U∞= 0.44 m·s-1;Re为3 000,出口设置为出流边界;假定圆柱为无限长,所以上、下面设置为对称边界;圆柱表面设置为无滑移壁面面边界。大涡模拟湍流模型选择动力Smagorinsky-Lilly 亚格子模型,Fluent 软件算法选用压力-速度耦合的SIMPLE 算法,离散方法为有界中心差分格式。
2 计算结果分析
2.1 升、阻力对比分析
为了验证本文数值结果的准确性,本文对直圆柱进行数值模拟,得出圆柱的气动性能,并与文献[7]中的结果进行对比,结果表1 所示。本文中直圆柱与文献[7]中数值结果的阻力系数仅相差2%,升力系数仅相差1%,表明结果可靠。表2为不同波形圆柱(WY-1、WY-2、WY-3)的平均阻力系数和升力系数与直圆柱对比。从表中可以看出,对于3 种不同振幅的波形圆柱a/Dm=(0.122 ∼0.182), λ/Dm=0.606,与直圆柱相比,阻力系数和升力波动都减少,尤其是升力波动得到了抑制;当a/Dm=0.152时,减阻效果最佳,达18.3%,其升力波动也减少了93%,说明对于Re为3 000 的波形圆柱绕流,存在最佳振幅使得减阻效果最大化。图4 为升、阻力系数时程曲线,表示直圆柱及不同振幅的波形圆柱的气动性能。从图中可以看出,当计算结果稳定后,阻力系数和升力系数均呈现周期性变化,直圆柱(CY)的振幅较大,同时平均阻力随着振幅增大而增大。从3 种波形圆柱的升、阻力系数时程曲线看,平均阻力系数均比直圆柱小,升力系数波动减小尤为明显,说明波形圆柱能有效地抑制升力波动。
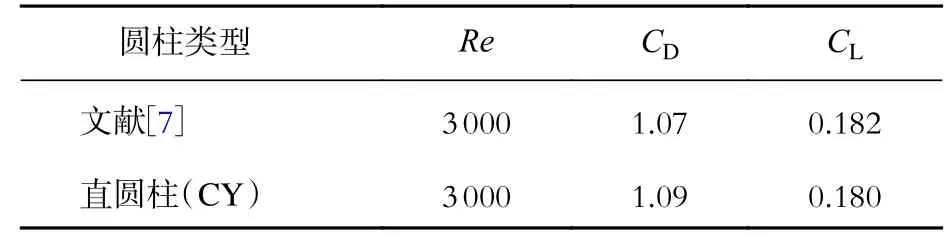
表 1 本文数值结果与文献结果对比Tab. 1 Comparison between the numerical results in this paper and the refence

表 2 波形圆柱与直圆柱升、阻力对比Tab. 2 Comparison of lift resistance between wavy cylinder(WY)and smooth cylinder(CY)
2.2 速度分析
通过对直圆柱和波形圆柱近尾迹区的流向速度及脉动速度分析,可以更加明显地反映其周围的流场结构。图5 为在圆柱尾迹x/Dm=3位置处无量纲顺流向时均速度分布,将3 种波形圆柱最大截面处(Node)[图5(a)]和最小截面处(Saddle)[图5(b)]尾迹速度分布与直圆柱的进行对比。由图中可以看出,在波形圆柱最大截面处,当y/Dm<1时,其尾迹流向时均速度小于直圆柱,当y/Dm>1时,尾迹流向时均速度大于直圆柱。在波形圆柱最小截面处,其交点约在y/Dm=0.5处,很明显,由于直径减小,对流体的阻力也随之减小,所以流体能够更快地通过。在最大截面处,由于阻力增大,流体通过速度减慢。这样的壁面变形梯度使得流体通过圆柱体时形成速度梯度,这样相比于直圆柱,在近尾迹处形成横向涡流的同时,也会产生流向涡,将原来尾迹处形成的大涡拉伸、破碎,进而改变近尾迹处流场结构。这一点从图6(a)中也可以看出,当/U∞<0时,波形圆柱/U∞<0区域均向后推移,且范围更广,说明近尾迹区域向下游偏移,流向涡增大。从图6(b)中可以看到,波形圆柱最大截面处和最小截面处中心线上的最大速度脉动均向后推移,且小于直圆柱。而对于同一波形圆柱,最小截面尾迹的速度脉动要低于最大截面尾迹的速度脉动。图7 为圆柱表面时均速度流线图。从图中可以看出,直圆柱壁面流动分离后形成再附着涡,增加了流动损失,而波形壁面结构产生的流向涡拉伸了尾涡,使得再附着涡消失。这说明波形圆柱尾迹动量损失更小,从而达到减阻目的。
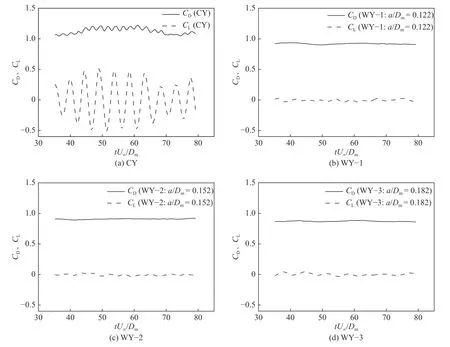
图 4 升、阻力系数时程曲线Fig. 4 Time history curve of lift resistance coefficient
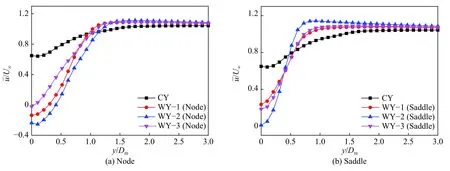
图 5 圆柱尾流x/Dm=3 位置上顺流向时均速度分布Fig. 5 Distribution of time-averaged streamwise velocity (/U∞) at x/Dm=3
2.3 涡结构分析
流体的湍流运动是由各种大小和涡量不同的涡旋叠加而成。流体在运动过程中涡旋不断破碎、合并。因此,明确流场中涡量的大小、变化和输运情况,对分析流动能量的耗损和规律有十分重要的参考价值。图8 为圆柱尾迹y=0 平面涡量云图。从图中可以看出:对于直圆柱,流体通过圆柱时,剪切层强烈卷起形成漩涡,然后在尾迹形成著名的周期性卡门涡街;对于波形圆柱,观察图8 可以看到,所有波形圆柱尾迹形成的涡流都得到推延和拉伸,并由于振幅不同,涡流推延的距离和拉伸长度不同,且从图6(c)中可看出,波形圆柱( WY-2,a/Dm=0.152)尾迹涡流更加均匀,高涡量区更少,说明存在最佳振幅,使得流向涡结构最大程度稳定剪切层,从而阻止其发展卷起成为成熟的涡流。
图9 为直圆柱与波形圆柱涡核心区分布与速度分布。从图中可知,直圆柱尾迹存在明显的卡门涡街,随着波形圆柱振幅的增加,卡门涡街现象变得不稳定,直至消失;波形圆柱[图9(b)~(d)]壁面的展向流动与流体分离形成的剪切流反应,形成流向涡,使得这些剪切层不太稳定,将原本的高涡量的卡门涡街拉伸、破裂,使得大尺度涡变成小尺度涡,改变了涡系的流向和展向分布,并且卷曲较弱,形成涡流,并在下游不断发展,形成更长的尾涡。以外,从图中还可以看出,当a/Dm=0.152时,涡结构更加平缓、稳定,说明存在最佳振幅,从而达到最大减阻的效果。
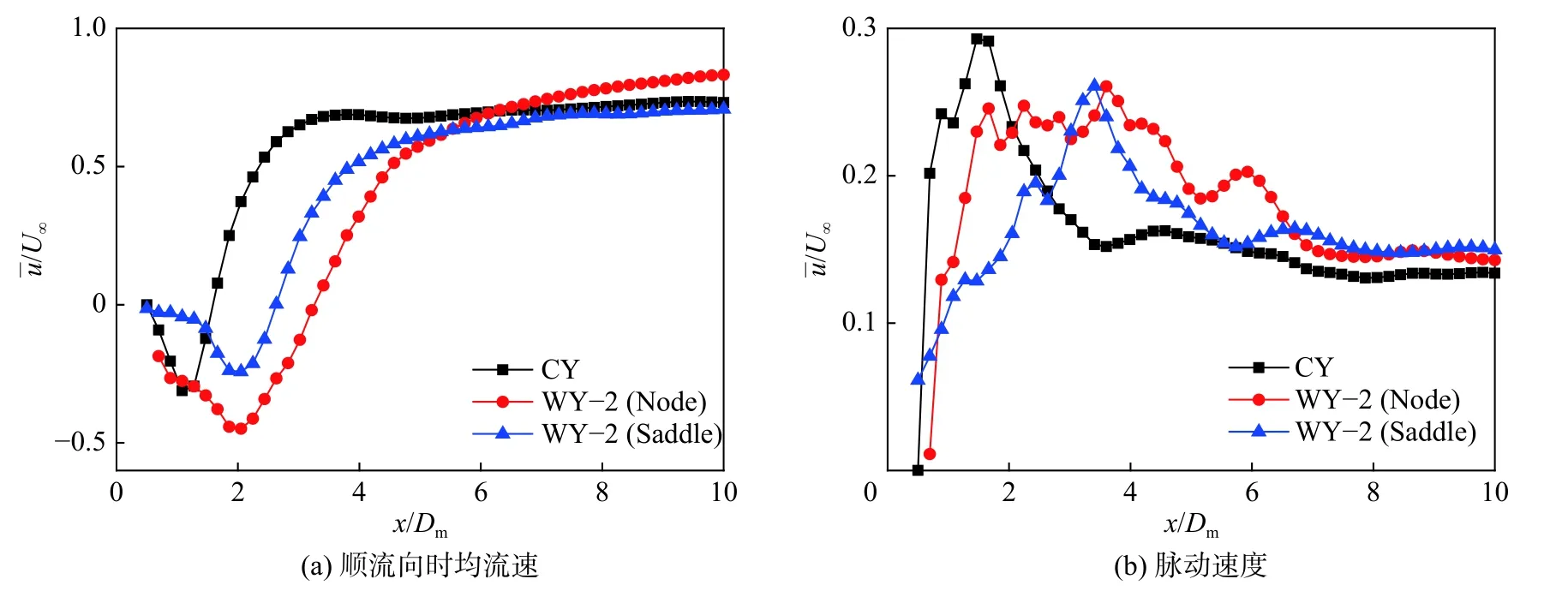
图 6 波形圆柱(WY-2)和直圆柱(CY)圆柱中心线上(y/Dm=0)速度分布Fig. 6 Distribution of velocity along the wake centerline (y/Dm=0) of wavy cylinder (WY-2) and smooth cylinder (CY).
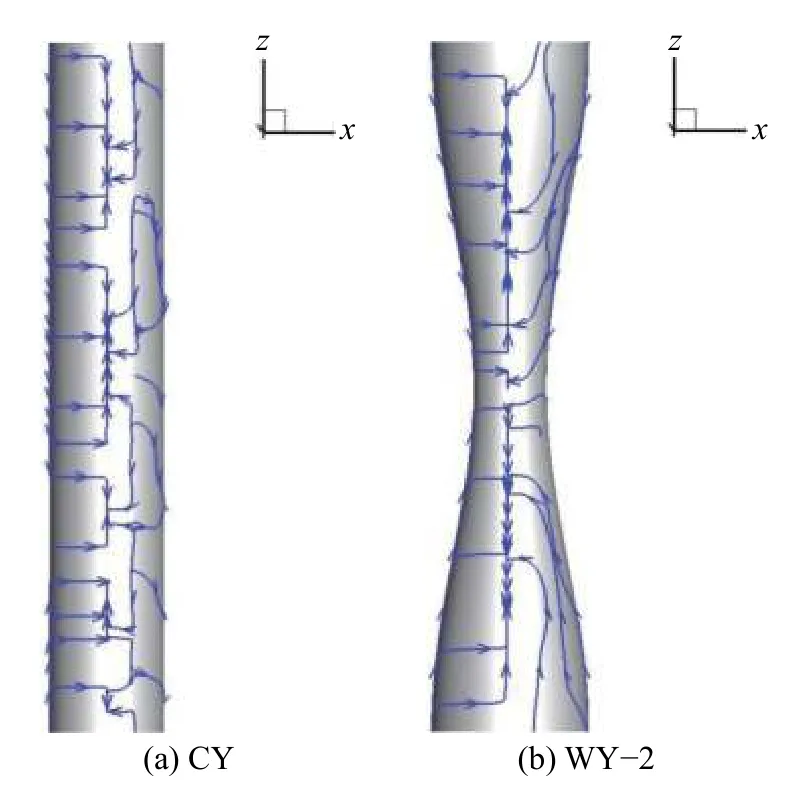
图 7 圆柱表面时均速度流线图Fig. 7 Time-averaged velocity streamlines on the surface of cylinder surface
3 结 论
本文通过三维大涡模拟对比研究相同雷诺数下不同振幅的波形圆柱与直圆柱近尾迹时均流速分布,以及非定常涡结构分析,得出以下结论:
(1)与直圆柱相比,波形圆柱尾迹大尺度涡结构减少,尾迹的涡系结构更为紧凑。说明波形圆柱壁面的变形结构能够显著影响圆柱尾迹涡核心区的结构,将大尺度涡拉伸破碎成小尺度涡,改变涡系的流向和展向分布。
(2)振幅的改变影响波形壁面附近的流向涡结构,且存在最佳振幅,使得流向涡结构最大程度稳定剪切层,从而阻止其发展卷起成为成熟的涡流,进而达到减阻目的。这对于亚临界下钝体绕流的减阻(水中行驶的船舶、桥梁、海上石油平台)有着重要的参考意义。
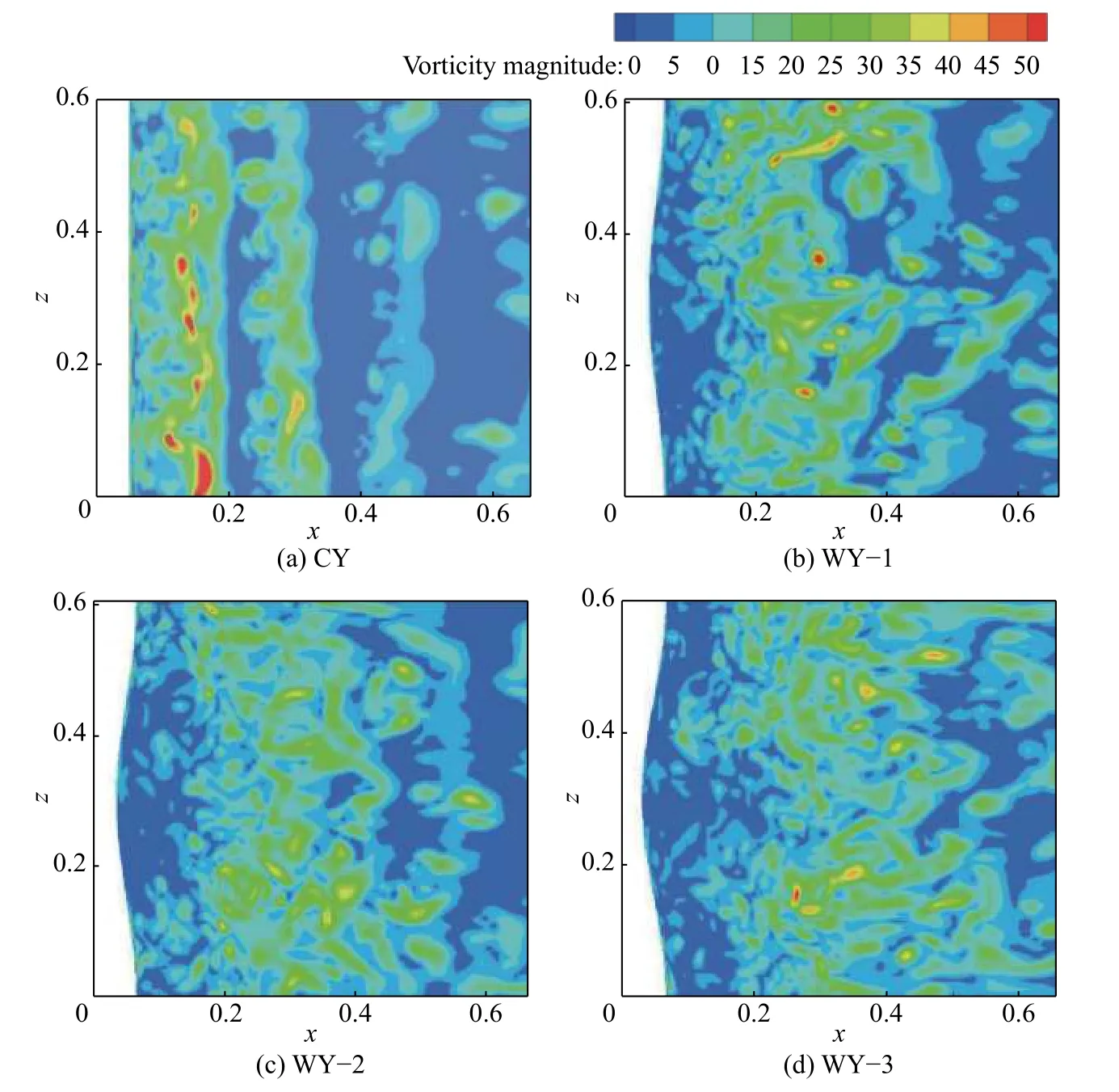
图 8 圆柱尾迹y=0 平面涡量云图Fig. 8 Vorticity cloud image at the surface y=0 near the wake region
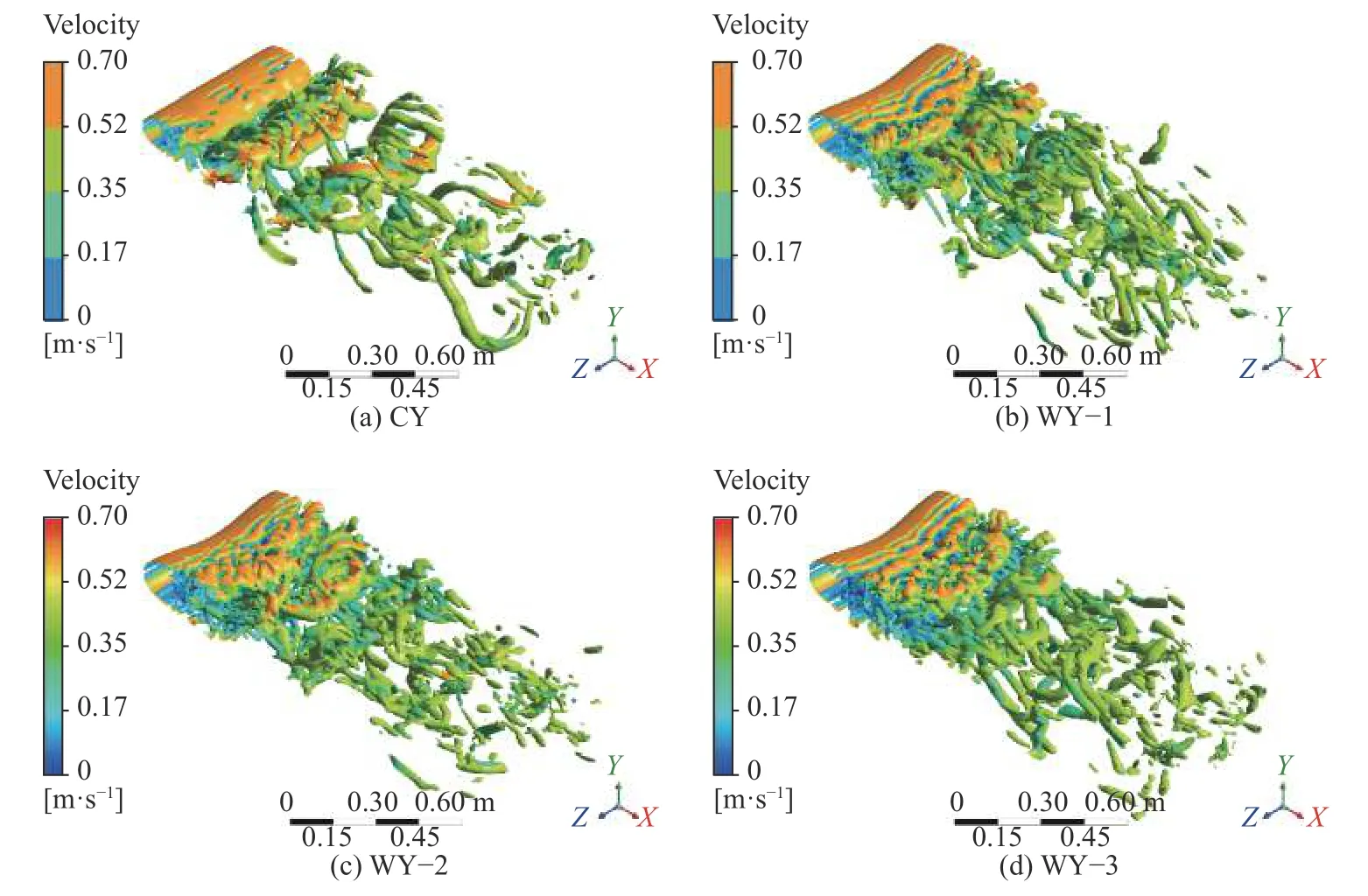
图 9 直圆柱与波形圆柱涡核心区分布与速度分布Fig. 9 Distribution of votex core and velocity for wavy cylinder and smooth cylinder
