气动柔性轴向驱动器结构与特性研究

(北华大学 机械工程学院， 吉林 吉林 132021)

引言

机器人技术不断发展，其应用领域也从传统制造业向家庭服务、医疗救援等行业扩展。软体机器人以其特有的环境适应性好、主动变形灵活等优势，受到国内外学者的广泛关注[1-5]。轴向驱动器作为机器人关节驱动单元的核心部件，其柔性程度成为了制约软体机器人发展的重要因素。目前常用的轴向驱动器有气压缸、液压缸、直线电机、电动缸等。气压缸、液压缸伸长量不可连续调整， 体积较大，使用不灵活， 柔性差；直线电机和电动缸虽然伸长量可控，精度高，但其本身结构复杂，体积较大，使用不灵活，难以实现小型化[6]。本研究提出的气动柔性轴向驱动器，具有轴向伸长量连续调整，调节驱动力等功能，能克服目前轴向驱动器体积大、柔性差、位置不可控等缺陷，同时具有易于控制、无污染等优点[7]，对软体机器人的发展具有重要的研究意义。

1 轴向驱动器结构设计

本研究所述气动柔性轴向驱动器，主要由上、下端盖，内、外弹性气囊，导向轴，内、外气囊约束件以及限位片组成，如图1所示。

1.快插接头 2.下端盖 3.外约束环 4.上端盖 5.导向轴 6.外弹性气囊 7.内弹性气囊 8.内约束环 图1 轴向驱动器结构

驱动器内、外弹性气囊为硅氟橡胶管，均采用机械密封方式与上、下端盖固定，与端盖形成环形截面的密闭腔体，其弹性模量E为1.116 MPa；硅橡胶具有良好的耐温性、绝缘性及耐腐蚀性，且无毒无味，在航空航天、医疗卫生及机械加工等领域具有广泛的应用[8-11]。下端盖设置有气体入口，使压缩气体能够进入腔体内，气体推动上端盖沿导向轴运动产生轴向推力，推力大小取决于通入的气体压力值；导向轴与下端盖采用螺纹方式固定在一起，且穿过上端盖中心孔，保证了驱动器运动方向的同时增强了驱动器横向刚度；气囊约束件包括内约束环和外约束环两种类型，两者均为圆柱环形结构，其中内约束环位于内弹性气囊内部，其外径尺寸与内弹性气囊内径尺寸相同，能够阻止驱动器工作时内弹性气囊的径向挤压与导向轴接触，减少运动阻力，且内径与导向轴间隙配合，便于内约束环沿导向轴移动；外约束环内径与外弹性气囊外径尺寸相同，嵌套于外弹性气囊外部，用于约束外弹性气囊的径向膨胀，使驱动器只能产生轴向伸长运动；限位片通过螺纹固定于上端盖上，防止外约束环脱落。驱动器本体结构参数如表1所示，d1、d2为外弹性气囊外径、内径，d3、d4为内弹性气囊外径、内径；L1、L2为外弹性气囊和内弹性气囊有效变形长度；d5、d6为外约束环外径、内径；d7、d8为内约束环外径、内径。

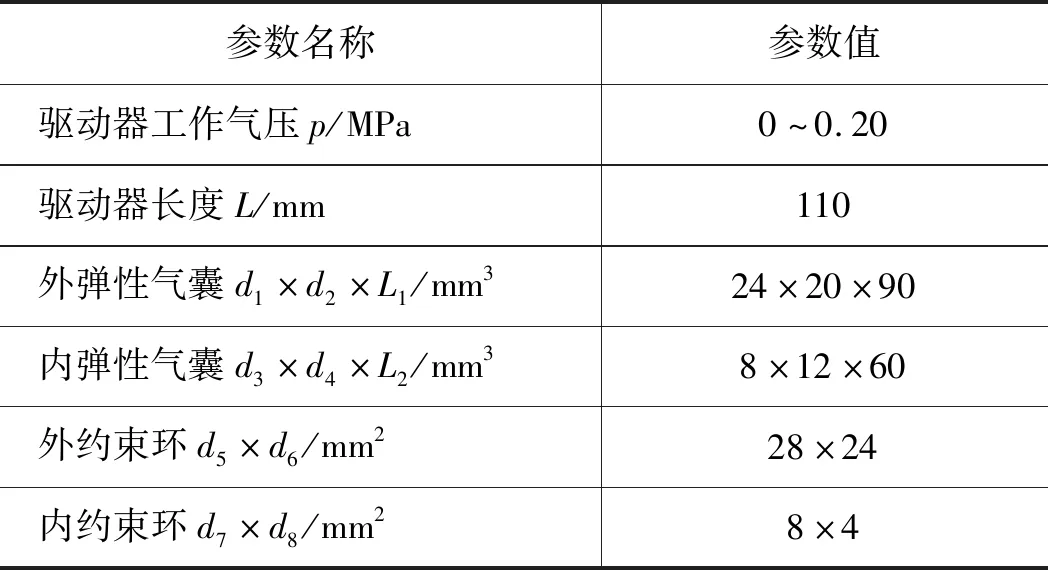
表1 轴向驱动器本体结构参数

2 轴向驱动器静力学性能研究

根据驱动器作用机理，研究其在不同气压下，驱动器驱动力、输出力及伸长量变化情况。

2.1 轴向驱动器工作原理及静力学理论模型

气动柔性轴向驱动器，以压缩气体为动力源，当压缩气体进入弹性气囊形成的密闭腔体内时，外约束环和内约束环分别限制外弹性气囊的径向膨胀和内弹性气囊的径向挤压，径向刚度较大，同时在导向轴作用下，驱动器只能沿导向轴产生轴向伸长变形。轴向驱动器密闭腔体内通入的气体压力越大，其轴向伸长量和驱动力也越大，随着伸长量增加，驱动器驱动力不断减小，当其伸长量到达极限位置时，驱动力为0。

图2 驱动器受力模型

驱动器工作时，上端盖在气压p作用下，产生轴向推力，并沿导向轴产生位移，同时对负载产生轴向驱动力，内、外气囊自身弹性将产生变形阻力，其受力模型如图2所示，由静力学平衡可知：

Fp=Fn+Fw+Fd

(1)

式中，Fp—— 轴向推力

Fd—— 轴向驱动力

Fn，Fw—— 内、外气囊产生的变形阻力

2.2 轴向推力

由作用力、压强及面积关系可知，驱动器腔体内压缩气体压力值及其产生对驱动器上端盖产生的轴向推力公式：

Fp=CpS

(2)

式中，C—— 驱动器变形不均匀系数，与气囊、约束环间接触状态有关

p—— 驱动器腔体内气体压力与外界大气压的差值

S—— 驱动器腔体有效工作面积

S=Swn-Snw

(3)

式中，Swn—— 外弹性气囊内腔横截面积

Snw—— 内弹性气囊的外横截面积

驱动器工作时，产生轴向推力同时存在轴向伸长变形，伸长量为ΔL，而内、外弹性气囊的体积(Vn、Vw)均未产生变化，假设内、外弹性气囊伸长量与驱动器整体伸长变形一致，故由体积公式V=SL可知，弹性气囊横截面积将产生变化。以外弹性气囊为例，研究产生伸长变形后气囊内腔横截面积Swn与伸长量ΔL的关系：

Vw=(Sww-Swn)L1

(4)

式中，Sww——外弹性气囊的外横截面积

L1—— 驱动器初始长度

由于外约束环作用，伸长变形中外弹性气囊的外径未发生变化，Sww保持不变，故变形后其体积公式为:

Vw=(Sww-S′wn)(L1+ΔL)

(5)

(6)

(7)

(8)

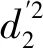
将式(6)～式(8)分别带入式(4)、式(5)并联立可得：

(9)

同理，由于内约束环的作用，内弹性气囊在伸长过程中内径不发生变化，可以推得变形后内弹性气囊外径为:

(10)

式中，d′3为内弹性气囊变形后的外径。

因此，驱动器轴向伸长后的有效工作面积:

(11)

此时，气压对驱动器上端盖产生的轴向推力:

(12)

从公式中可以看出，由于驱动器工作中存在轴向长度变化，导致有效工作面积发生变化，致使压缩气体对上端盖产生的轴向推力呈非线性变化。

2.3 驱动力

驱动器内、外弹性气囊所采用的硅氟橡胶，属于超弹性体，其受外界拉力产生轴向变形时，自身阻力对驱动器驱动力及伸长变形影响较大。

由于内、外约束环作用，驱动器内通入压缩气体时，气囊变形符合拉压杆大变形[12]，采用弹性力学的经典理论，并结合驱动器变形因素，内、外气囊的作用力进行分析为:

(13)

(14)

式(13)、式(14)中，An、Aw分别为内、外弹性气囊变形后的环形截面面积：

(15)

(16)

分别将式(15)、式(16)带入式(13)、式(14)中可得：

(17)

(18)

由驱动器静力平衡方程式(1)可知，驱动器产生的轴向驱动力为：

Fd=Fp-Fn-Fw

(19)

将式(12)、式(17)、式(18)分别带入式(19)得：

(20)

由驱动力式(20)可知，当工作气压p一定时，随着伸长量ΔL增加，驱动力减小；伸长量一定时，随工作气压的增加，驱动力不断增大；伸长量为0时，驱动力最大，即气压对驱动器端盖产生的轴向推力。

2.4 伸长量

驱动器气压-伸长量变化状态受工况变化影响较大，在此仅研究处于空载(Fd=0)、上端盖自由轴向移动状态下气压-伸长量性能。分别将式(12)、式(17)、式(18)分别带入式(19)并简化可得式(21)，由式(21)可以看出，驱动器伸长量ΔL′与气压值为非线性关系。

(21)

3 轴向驱动器静力学特性实验

静力学性能是影响驱动器工作能力的重要参数，主要包括伸长量及驱动力特性。通过搭建静力学实验平台，研究驱动器气压-伸长量及气压驱动力特性对驱动器的应用有重要意义。

3.1 驱动力特性

驱动器气压-驱动力实验原理如图3所示。将驱动器下端盖固定于实验台上，利用X、Y移动滑台调整测力计与驱动器上端盖的位置，使两者接触；精密减压阀调节通入驱动器内部的气体压力，并通过气压传感器对内部气体压力值进行检测，在压缩气体作用下驱动器上端盖将沿导向轴移动并挤压测力计，进而将驱动器的驱动力测量出来。

根据实验原理搭建了驱动器气压-驱动力实验平台如图4所示，研究驱动器零位移状态下和恒定位移状态下的驱动力性能。实验装置主要包括气源、精密减压阀、测力计、气压传感器、X、Y移动滑台、轴向驱动器、连接件及其保持架，主要实验装置参数如表2所示。由于驱动器导向轴长度大于驱动器本体，所以实验装置中增加了连接件以及连接件保持架，确保实验过程中驱动器与测力计紧密接触的同时两者轴线处于同一直线上。

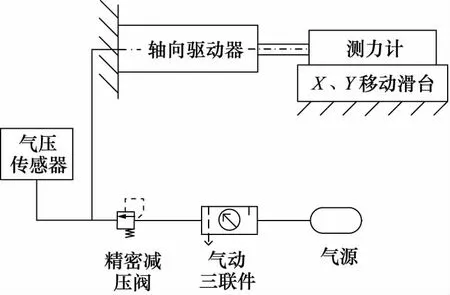
图3 气压-驱动力实验原理

图4 气压-驱动力实验装置

表2 气压-驱动力实验装置参数表

驱动器零位移(ΔL=0)驱动力性能实验研究中，控制通入驱动器的气体为0.02～0.18 MPa等梯度压力，分别读取不同压力下测力计数值，并绘制气压-驱动力变化曲线如图5所示。通过式(20)对驱动器气压-驱动力理论值进行计算，并与实验值进行对比可知驱动器变形不均匀系数C为1.5。由图5驱动器气压-驱动力变化曲线可以看出，驱动器驱动力实验值与理论值变化曲线具有较好的一致性：随气压值增大，驱动力呈线性增加。

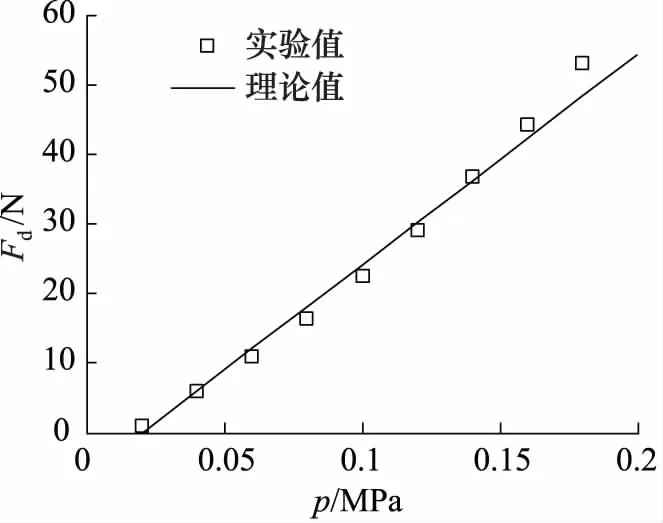
图5 气压-驱动力变化曲线

驱动器恒定位移驱动力性能试验中，通过X、Y移动滑台，调整测力计与驱动器之间的距离(5～25 mm等间距)，并将通入驱动器内部的气体压力值划分为5个等级(0.06～0.14 MPa)，分别研究在相同气压下，驱动力随位移变化情况以及在相同位移下驱动力随气压变化情况。驱动器位移-驱动力变化曲线如图6所示，由曲线可以看出，相同气压下，随位移增加，驱动器驱动力不断减小；位移恒定时，气压越大，驱动器驱动力越大，与理论推导式(20)结论相符。

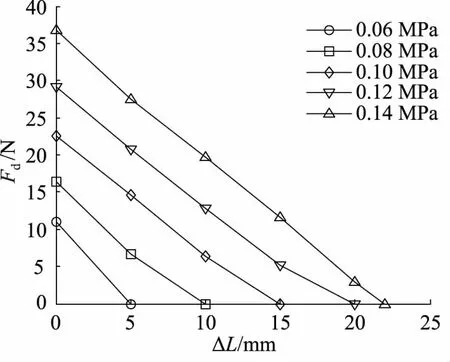
图6 位移-驱动力变化曲线

3.2 伸长量特性

实验原理如图7所示，将标记点固定于驱动器上端盖，当驱动器内部通入压缩气体时，上端盖将带动标记点沿导向轴产生轴向位移。利用三维运动捕捉系统读取标记点位移变化，处理器将数据上传至计算机，通过计算可得到驱动器气压-伸长量变化曲线。

图7 气压-位移实验原理

根据实验原理完成实验平台的搭建如图8所示。轴向驱动器下端盖垂直于地面固定在实验台上，三维运动捕捉系统(NDI Certus)中的视觉传感器垂直于标记点所在平面，能够准确读取标记点Y坐标变化。实验中，分别读取标记点在不同气压(0.02～0.18 MPa)下的坐标值，通过计算，可得到驱动器气压-伸长量变化数据曲线，如图9所示。由气压-伸长量变化曲线可以看出，随气压值增加，驱动器伸长量不断增大，且呈非线性关系，与理论值拟合程度较好。

图8 气压-伸长量实验装置

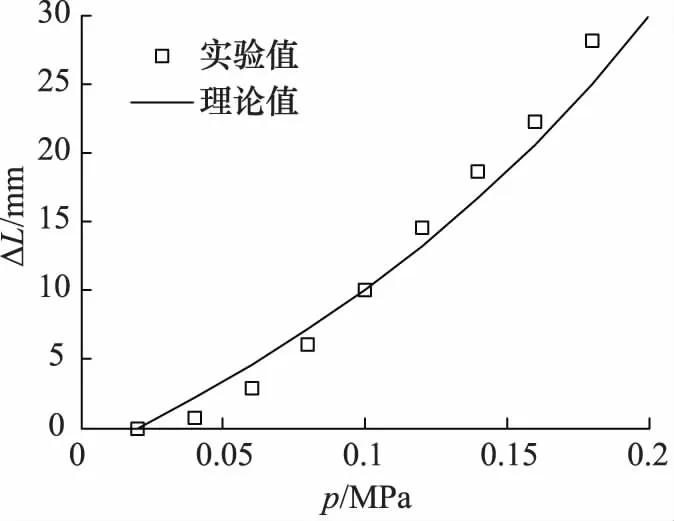
图9 气压-伸长量变化曲线

4 结论

本研究针对传统驱动器体积大，柔顺性差，位姿不可连续调节等问题，设计了正压驱动型气动柔性轴向驱动器，并对该驱动器力学特性进行了理论与实验分析。理论分析与实验结果均表明：气动柔性轴向驱动器，结构设计合理，具有轴向伸长和驱动功能；驱动器伸长量可实现连续调整，且随气压值增加呈非线性增加，气压为0.18 MPa时，最大伸长量为28.1 mm；驱动器轴向输出力随伸长量增大而减小；伸长量为0时，驱动具有的轴向驱动能力最大，且随工作气压的增大呈线性增加，气压为0.18 MPa时，最大轴向输出力为52.04 N。该气动柔性轴向驱动器，能够克服目前机器人驱动器柔性不足问题，可针对工作要求调整驱动力与伸长量，为机器人技术的研究与发展奠定了理论与实验基础。