展向凹槽及泄流孔对高超声速平板边界层转捩影响的试验研究*

李强 赵磊 陈苏宇 江涛 庄宇 张扣立†

1) (中国空气动力研究与发展中心超高速所,绵阳 621000)

2) (中国空气动力研究与发展中心计算所,绵阳 621000)

3) (天津大学力学系,天津 300072)

针对展向凹槽和泄流孔对高超声速钝平板边界层转捩的影响,在中国空气动力研究与发展中心Φ2 m激波风洞(FD-14A)开展了试验及初步的计算与理论研究.试验的来流马赫数为6、单位雷诺数为3.3×107 /m,平板的前缘半径为1 mm,攻角为—4°.在距平板前缘110 mm处布置三组不同的二维展向凹槽,凹槽的宽度与深度分别为凹槽1 (2.5 mm,1 mm)、凹槽2 (3.75 mm,1.5 mm)、凹槽3 (5 mm,2 mm),同时凹槽1的两端可以打开泄流孔,记为凹槽4,不含凹槽时的光滑平板情况记为凹槽5或平板.采用热流传感器测量了不同情况下平板中心线的热流分布,测量结果显示,光滑平板情况在x ≈ 340 mm处开始转捩,在x ≈ 425 mm处转捩接近完成.凹槽导致平板边界层的转捩位置提前,且随着凹槽宽度及深度的增加,对转捩的促进作用增强,转捩位置向上游移动.凹槽1增加泄流孔后(凹槽4)其热流分布及转捩位置与光滑平板情况基本一致.边界层流动完全转捩为湍流后,各情况下的热流差别较小,表明不同规格的凹槽只影响转捩过程中的热流分布,对转捩完成后的湍流壁面热流影响较小.数值计算 (CFD)结果显示,泄流孔导致了被动抽吸,试验结果显示凹槽两端的泄流孔抽吸效应抵消了凹槽对平板中心线边界层转捩的促进作用.采用线性稳定性理论(LST)及最优扰动方法分析了光滑钝平板情况的流动失稳机制.LST结果显示,本文平板流动不存在Mack第一模态、第二模态失稳,因此传统的模态失稳机制无法解释试验中观测到的转捩现象.最优扰动计算显示,平板流动存在较强的非模态失稳,可以定性解释观测到的转捩现象.

1 引 言

高超声速边界层转捩导致表面热流和摩阻增大3—5倍,严重影响高超声速飞行器气动力/热特性,边界层转捩预测技术是高超声速飞行器研制过程中的关键技术之一.高超声速边界层转捩是当前空气动力学的前沿领域和热点问题之一,国内外专家在转捩机理、预测和控制方面做了大量的研究工作,也取得了一系列研究成果[1-3].其中有很多工作研究飞行器表面凹陷结构对高超声速边界层转捩的影响,早期的文献[4-7]对凹坑/二维轴对称凹槽带来的压力振荡、分离流动、转捩、热流密度增量等问题进行了研究.2003年美国哥伦比亚号航天飞机失事后,美国NASA兰利中心[8-12]利用20 in (1 in=2.54 cm) M6风洞、31 in M10风洞、20 in CF4风洞,针对航天飞机模型和平板模型开展风洞试验,研究凹坑对转捩的影响,并通过数值计算研究不同长-深比的凹坑对凹坑内部及下游流动的影响、对转捩及壁面热流密度的影响.研究工作表明高超声速条件下,凹坑对转捩的影响依赖于凹坑的长-深比、长-宽比、深度与边界层厚度的比值等,流向更长、展向更宽、深度更深的凹坑更容易促使下游边界层转捩.高超声速条件下凹坑流动比较复杂,带来流动分离、剪切层失稳、激波-涡、激波-激波、激波-边界层干扰等问题.相关文献[12-14]认为,凹坑的流向尺度是决定其对转捩影响的重要因素;凹坑后向台阶可诱导纵向长涡,涡破碎促发转捩;正是凹坑引起的下游剪切层流动导致了边界层转捩.目前对于平板展向凹槽的研究不多,文献[15]总结了低速条件下机翼表面展向凹槽对转捩的影响,展向凹槽深度和宽度参数都对转捩有影响,并明确了基于凹槽宽度的转捩临界雷诺数;并基于线性稳定性理论,分析认为展向凹槽影响转捩的原因主要是放大T-S波和产生新的不稳定机制.

壁面抽吸[16-17]与粗糙元、壁面振动以及壁面加热等现象属于壁面扰动感受性问题,而声波、涡波以及熵波是自由流扰动感受性问题.在航空领域,壁面抽吸延迟边界层转捩得到了比较系统的研究,也获得了成熟的应用.为了降低飞机巡航时的摩擦阻力,采用了延缓机翼边界层转捩的层流流动控制技术,其中最有效的层流控制技术是混合层流控制技术[18-27],它是在层流翼型的基础上,通过在机翼前缘壁面吸气实现层流流动控制.文献表明,吸气量是影响层流控制效果的关键因素,不合适的吸气量会使层流控制效果丧失;并且机翼前缘上表面壁面吸气不会明显影响壁面压力分布,因而机翼升力不会有明显的变化;壁面吸气稳定边界层包含两种机制:其一是改变边界层平均速度分布来获得更稳定、更饱满的速度剖面;其二是减小边界层位移厚度雷诺数.在高超声速领域,赵耕夫[28]根据可压缩黏性稳定性理论研究了高超声速圆锥模型表面边界层对转捩的影响,边界层抽吸对第一、二模态都起稳定作用.Wang和Zhong[29]采用线性稳定性理论(LST)和直接数值模拟(DNS)的方法,研究了半锥角5.3°尖楔M8高超声速边界层受壁面吹吸扰动的感受性机理问题.研究结果证实,壁面吹吸扰动频率影响一模态和Mack模态的同步点位置,如果抽吸区域位于同步点上游,不稳定二模态会被激发,反之则不会被激发.

在高超声速条件下展向凹槽对转捩的研究文献较少,没有相关文献将泄流孔与展向凹槽结合,研究结合体对边界层转捩的影响.因此本文在平板表面研究展向凹槽对边界层转捩的影响,并研究凹槽与泄流孔结合体对边界层转捩的影响,在激波风洞M6流场条件下开展试验,采用热流传感器测量平板中心线热流的方式来判断转捩.本文第2节简要介绍了开展风洞试验的设备、试验模型、测量手段、风洞流场条件等;第3节给出了展向凹槽对平板边界层转捩影响的试验结果和计算结果对比;第4节给出了泄流孔对平板转捩影响的试验结果和计算结果分析讨论;第5节给出了平板边界层失稳机制理论分析;第6节给出结论.

2 试验设备、模型及流场条件

2.1 试验设备及测量手段

试验在中国空气动力研究与发展中心超高速所Φ2 m激波风洞(FD-14 A)上开展,试验设备由激波管、相应喷管、试验段、真空箱组成,激波管的内径为150 mm,其高压段和低压段的长度分别为9 m和18 m.风洞试验气体为氮气,采用氢气或氢气-氮气混合气体驱动,驱动压力目前可达50 MPa.通过更换喉道或喷管可获得不同的来流马赫数,通过调节高、低压段的压力可获得不同的来流单位雷诺数,以实现不同的模拟环境.目前该风洞能模拟的马赫数范围为6—16,雷诺数范围为2.1×105—6.7×107m—1,其型面喷管出口直径为1.2 m,试验段的横截面积是2.6 m×2.6 m,试验的有效时间为4—18 ms.

试验所采用的测量手段[30-31]为Φ2 mm柱状热流传感器(图1),该传感器以玻璃为基底材料,制作成直径2 mm,长度20 mm的玻璃棒,采用真空磁控溅射镀膜方法在抛光的圆端面镀铂薄膜,连接测试引线制作成传感器,以铂薄膜测量模型表面热流.在平板表面安装热流传感器测量热流沿流向的分布,可用来判断边界层的转捩位置[31-33].

2.2 试验模型及流场条件

平板模型尺寸及测点布置如图2所示,平板长450 mm、宽350 mm,展向凹槽中心线到前缘的距离为110 mm,凹槽长200 mm.如图2所示,在平板中心线布置22个测点.为了研究不同尺寸的展向凹槽对平板转捩的影响,加工了三种规格的凹槽,如图3所示,凹槽的宽度与深度分别为凹槽1(2.5 mm,1 mm)、凹槽 2 (3.75 mm,1.5 mm)、凹槽3 (5 mm,2 mm),凹槽4的宽度和深度与凹槽1一致,但在凹槽的两端增加了泄流孔,记为凹槽4,无凹槽时的填充替换件记为凹槽5或平板.

图1 Φ2 mm柱状热流传感器Fig.1.The Φ2-mm-diameter cylindrical heat flux sensors.

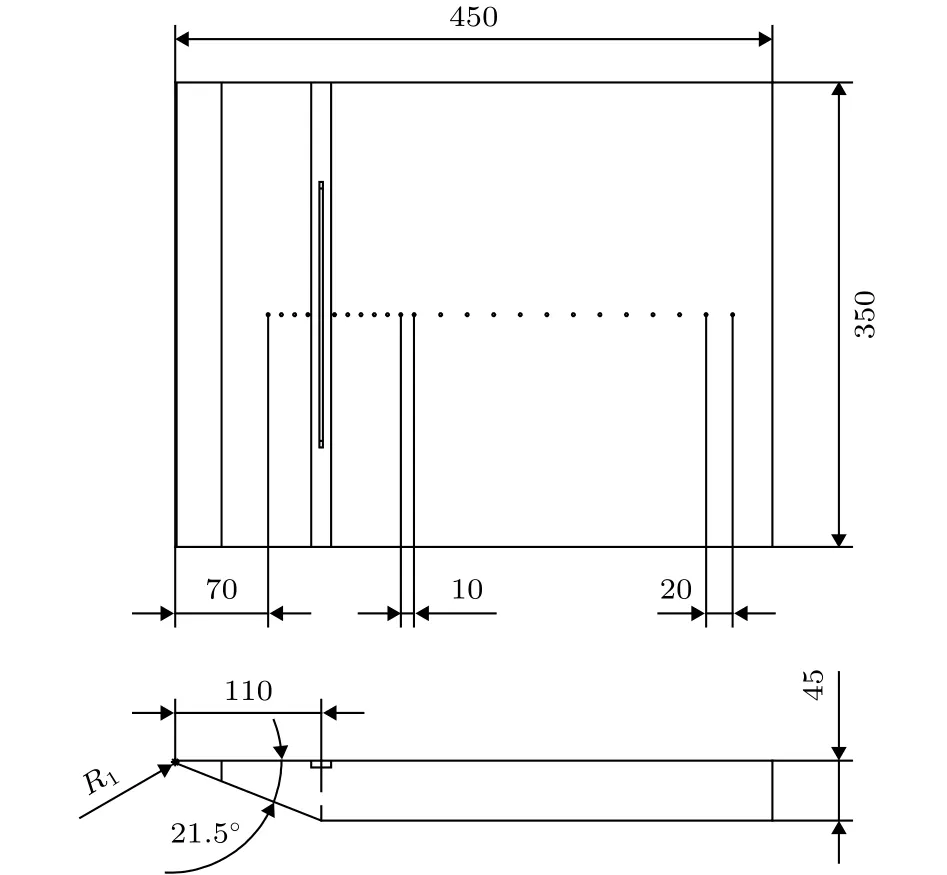
图2 平板凹槽测点分布示意图Fig.2.Schematic diagram of measuring point distribution.

图3 不同尺寸凹槽对比图Fig.3.Comparison chart of different size grooves.

如图3所示,凹槽4左右两端分别有一个泄流孔,孔长5 mm,孔宽度与凹槽宽度保持一致2.5 mm.在平板模型内部开孔联通到模型底面,泄流孔出口上游安装挡块,使泄流孔出口位于挡块背风区(图4),保证泄流孔出口压力比泄流孔入口压力低,以满足泄流条件.

图4 凹槽4泄流孔出口Fig.4.The discharge hole outlet of Groove 4.

风洞来流马赫数为6.0,单位雷诺数为3.3×107/m,来流静温87 K,来流静压4478 Pa,气流速度 1133 m/s,模型攻角为—4°.

3 凹槽对平板转捩的影响

采用热流传感器测量了光滑平板(无凹槽)及各凹槽影响下的平板中心线的壁面热流,图5给出了各情况下的热流分布;同时CFD计算了全层流与全湍流状态下的热流曲线分布,如图5中的实线所示.对于平板情况,在x ≈ 340 mm之前,试验测得的热流变化较为平缓,符合层流的热流分布特征,与层流状态下的CFD计算结果也较为符合.在x ≈ 340 mm之后,测得的热流显著增加,表明流动在x ≈ 340 mm处开始转捩,逐渐向湍流状态过渡,但在最后一个测点处仍未完成转捩.对于凹槽1工况,热流测量结果显示,中心线边界层从x ≈ 150 mm处开始转捩(凹槽中心线在x=110 mm),热流测量结果离开层流计算结果趋势线向湍流计算结果趋势线靠近,在x ≈ 200 mm处完成转捩.对于凹槽2工况,边界层转捩开始位置大约提前到凹槽下游第二个测点处(x=130 mm),转捩完成位置在x ≈ 180 mm.对于凹槽3(5 mm)工况,边界层大约从凹槽下游第一个测点(x=120 mm)开始转捩,转捩完成位置在x ≈ 180 mm.

从图中可以看出,凹槽下游x ≈ 120—300 mm范围内,随着凹槽尺寸的增大,凹槽下游中心线测点热流跟随增大;但在x＞300 mm之后,不同规格尺寸凹槽影响下的中心线测点热流趋于一致,分析认为x＞300 mm区域是边界层完全转捩成湍流之后的热流结果,其热流已经不受凹槽扰动的影响.因此凹槽对下游热流的影响分两部分区域,其一是x ≈ 120—300 mm范围内,凹槽扰动诱导边界层开始转捩,中心线热流开始升高,而不同规格尺寸凹槽的扰动强度差异会导致热流差异;其二是x＞300 mm区域,边界层完全转捩成湍流之后,凹槽扰动的影响基本可以忽略不计,不同规格尺寸凹槽影响下的中心线热流趋于一致,此时热流数值主要受来流参数和模型条件的影响,这与笔者之前开展的粗糙元强制转捩研究[31]结论一致.

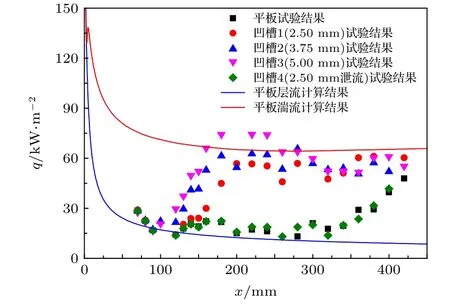
图5 平板中心线热流测量结果与计算结果Fig.5.The heat flux measurement and CFD results of the flat centerline.

平板无凹槽时,其中心线热流从x ≈ 320 mm位置开始呈升高趋势,到中心线最后一个测点(x=420 mm),中心线热流升高到接近湍流条件下热流相当的水平,说明此处边界层已经发展到接近完成转捩的状态.可以推论,如果平板长度能够增长,则边界层最终能完成转捩至湍流流态,中心线热流会稳定下来,并与平板湍流计算结果和凹槽影响下中心线热流测量结果相当.

4 泄流孔对平板流动的影响

图5中凹槽 4的尺寸与凹槽1一致 (宽度2.5 mm,深度1.0 mm),如图3所示增加2.5 mm×5.0 mm的泄流孔后,依靠平板模型上下表面的压力差形成被动泄流效果.图6给出了泄流孔中心轴线压力分布,y=0 mm位置处为平板表面,y=0— —45 mm区域为泄流孔内部,泄流孔上游平板表面边界层厚度为0.67 mm.从图6可以看出,沿泄流孔中心轴线压力从边界层外缘处大约8000 Pa开始降低,在进入泄流孔入口处压力呈现震荡,最后在泄流孔内部及出口处压力大致在3000 Pa左右.总体来说,平板上表面(即传感器测试面)与下表面保持了大约5000 Pa的压力差.

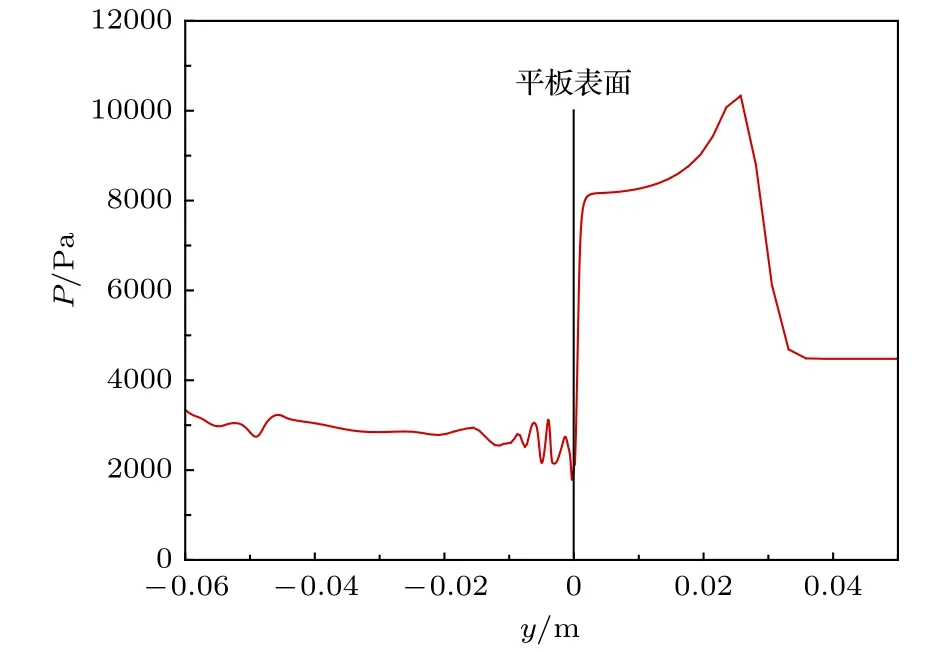
图6 泄流孔中心轴线压力分布Fig.6.Pressure distribution at the center axis of the discharge hole.

从图5中试验结果看,相对于凹槽1来说,在凹槽4泄流孔抽吸效果的影响下平板中心线边界层转捩延迟,并且凹槽4平板中心线热流与平板(无凹槽时)中心线热流基本相当,泄流孔抵消了凹槽的转捩促进作用.

对于泄流孔延迟转捩的问题,图7给出了泄流孔入口区域中心流向剖面总温分布图,可见泄流孔上游的边界层气流被抽吸进入泄流孔内部,下游边界层重新发展,因此导致边界层转捩延迟.其原理与航空机翼边界层层流控制中采用的边界层抽吸以及高超声速静音风洞层流喷管技术中采用的喉道边界层抽吸原理类似.

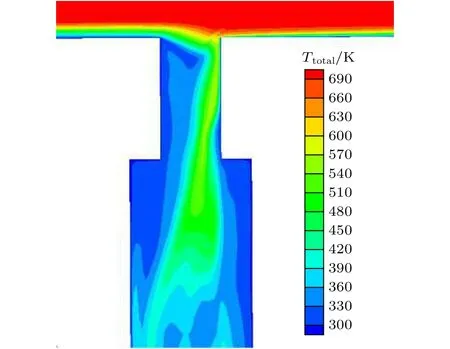
图7 z=97.5 mm剖面总温分布图Fig.7.Total temperature distribution of z=97.5 mm profile.

本次试验外侧两个泄流孔展向横跨100 mm距离,导致平板中心线边界层转捩延迟的原因,还需要深入研究分析.图8和图9分别给出了凹槽1和凹槽4中心对称面凹槽局部区域总温分布图,从图9可以看出,虽然凹槽4泄流孔存在边界层抽吸情况,但凹槽4中心对称面位置处凹槽上下游边界层,相对于凹槽1(图8)工况来说几乎没有变化,凹槽4中心对称面位置处边界层没有受到泄流孔抽吸的影响.对详细计算结果的分析对比,能证明泄流孔只对下游及其附近边界层产生影响,中心对称面处边界层流动参数不会受到影响.

图8 凹槽1中心对称面总温分布图Fig.8.Total temperature distribution of the symmetry plane of Groove 1.

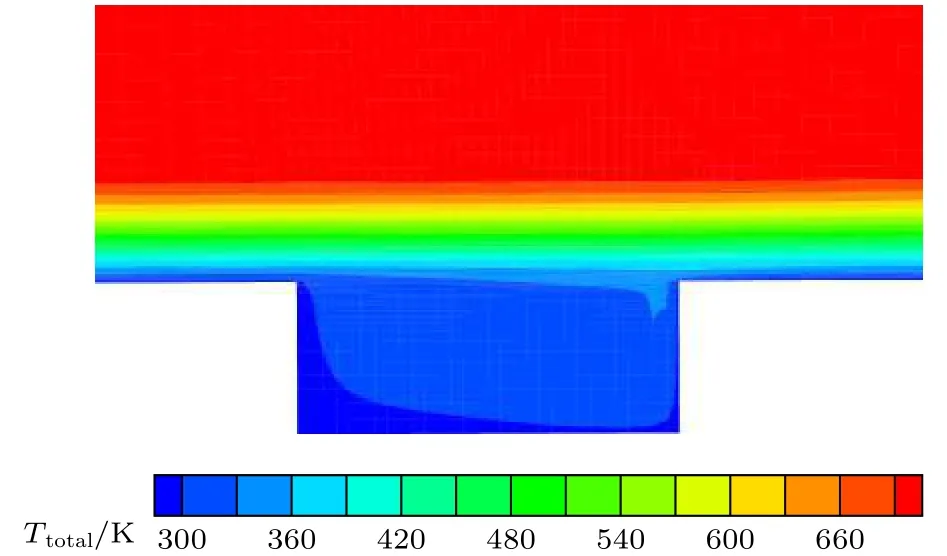
图9 凹槽4中心对称面总温分布图Fig.9.Total temperature distribution of the symmetry plane of Groove 4.

图10给出了凹槽4及泄流孔展向剖面横向速度分布,可以看出,由于泄流孔的抽吸效应,在凹槽内部存在指向泄流孔的横向流动,但横向流动速度不高.从试验结果来看,猜测可能就是这些凹槽内部的横向流动,导致凹槽4相对凹槽1的延迟转捩效果.而试验结果也显示凹槽4下游中心线热流与平板无凹槽时中心线热流基本相当,这是由于泄流孔抽吸效果引起凹槽4内部横向流动抵消了凹槽对下游平板的扰动,还是一种巧合,目前不能给出明确的答案,需要进一步深入研究.

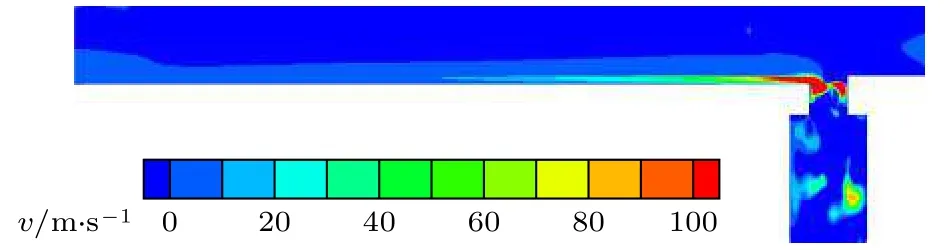
图10 x=110 mm剖面横向速度分布Fig.10.Transverse velocity distribution of the profile x=110 mm.

5 平板边界层失稳机制的理论分析

采用LST分析了光滑平板(无凹槽)边界层的稳定性特征.结果发现0°攻角条件下,LST分析未发现不稳定的第一模态波,在x=280 mm后开始出现第二模态失稳;在试验模型长度范围内,第二模态失稳波的最大N值约0.18,因此第二模态扰动的能量最多增长约0.4倍,不可能由该模态促发转捩;而在0°攻角的平板试验中也确实未观测到转捩现象.—4°攻角条件下,在试验模型长度范围内未发现第一模态及第二模态不稳定波,事实上,在距前缘1000 mm的下游才发现了第二模态失稳区,如图11所示.但是试验中明确地观测到—4°攻角钝平板的转捩现象,且转捩在x=400 mm处已经完成.说明转捩发生在模态失稳的临界雷诺数之前,因此,模态失稳(第一模态、Mack第二模态)的概念无法解释该模型的转捩现象.

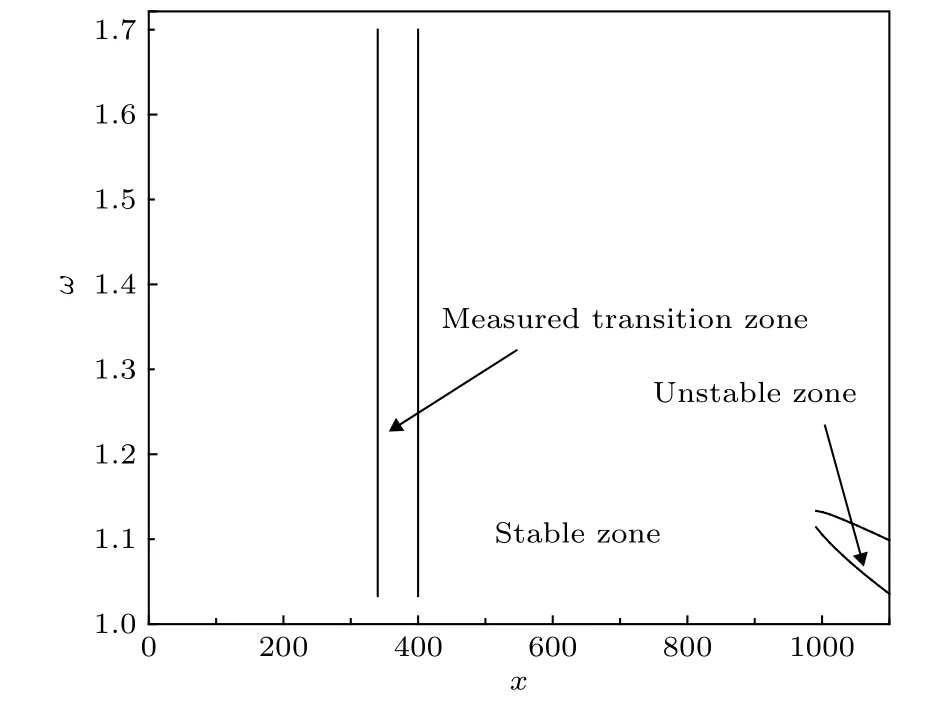
图11 —4°攻角平板边界层第二模态不稳定区Fig.11.The unstable zone of Mack second-mode waves for the cases of —4° attack angle.

采用最优扰动方法[34]研究钝平板模型的非模态失稳(瞬态增长).以—4°攻角平板为例,计算了不同区间的最优扰动的能量增长倍数,也称最优能量增益G.图12给出了固定入口x0及固定出口x1时不同计算域的最优能量增益G.当固定入口x0=2时,随着计算域向下游拓展,低展向波数的最优能量增益逐渐增加,高展向波数的最优能量增益逐渐降低,最优扰动的能量最大可增长约2400倍.最优展向波数则随着计算域向下游延伸而降低,即展向波长增加.随着边界层的发展,边界层厚度迅速增加,因此最优扰动的展向空间尺度可能与边界层厚度正相关.当固定出口x1=400时,随着计算域入口从上游向下游移动,最优能量增益先增加后减小,说明存在最优入口位置,最优扰动的能量最大可增长约5600倍.最优扰动的计算结果表明钝平板流动确实存在较强的非模态失稳,非模态失稳可能是导致试验中转捩的内在物理机制.

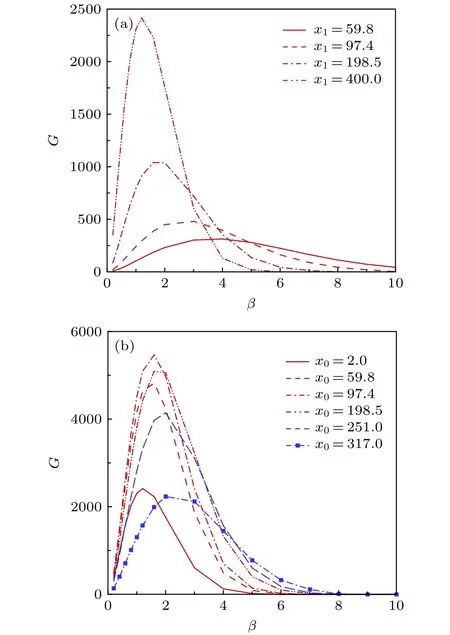
图12 固定入口x0 (a)和出口x1 (b)时不同计算域的最优能量增益Fig.12.Dependence of the optimal energy gain on the computational domain for fixed inlet location (a) and outlet location (b).

6 结 论

在激波风洞马赫数6、单位雷诺数3.3×107/m流场条件下开展试验,研究平板展向凹槽和泄流孔对转捩的影响,平板攻角—4°,凹槽宽度为2.50,3.75,5.00 mm三种规格,采用热流传感器测量平板中心线热流的方式来判断转捩.试验结果表明,凹槽导致平板边界层转捩位置提前,并使得原平板(无凹槽时)未完成转捩的边界层很快转捩成湍流;随着凹槽宽度增大,转捩位置向上游移动.边界层完全转捩成湍流之后,凹槽扰动的影响基本可以忽略不计,不同规格尺寸凹槽影响下的中心线热流趋于一致,此时热流数值主要受来流参数和模型条件的影响.

凹槽4外侧的两个泄流孔引发边界层被动抽吸效果,导致凹槽4相对凹槽1 (相同尺寸)的平板中心线边界层转捩延迟.但试验结果显示凹槽4下游平板转捩位置与平板无无凹槽时基本一致,两种工况下平板中心线热流基本相当,相当于泄流孔被动泄流效应正好抵消了凹槽对下游的扰动.分析认为可能正是由于泄流孔抽吸效应在凹槽内形成的横向流动,展向横跨100 mm左右距离,抵消了凹槽对平板下游中心线的扰动作用,但这也有可能只是一种巧合,需要进一步深入研究.

对激波风洞试验条件下的钝平板边界层转捩的机理进行了初步分析.—4°攻角的钝平板流动不存在第一模态及第二模态失稳,因此模态失稳理论无法解释试验观测到的钝平板边界层转捩现象.最优扰动计算表明钝平板流动存在较强的非模态失稳,线性最优扰动的能量最大可增长约5600倍.因此非模态失稳可能是导致钝平板边界层转捩的重要机制,展向凹槽及泄流孔对钝平板边界层转捩的影响,也可能与非模态失稳机制有关.

本文试验条件下观察到了展向凹槽促进平板边界层转捩位置提前,这需要在失稳机制方面进一步深入开展理论研究.另外泄流孔导致边界层转捩延迟早已得到确证,本文中展向凹槽外侧两个泄流孔导致中心对称面转捩延迟,这是新发现的试验现象,需要在机理方面深入研究.这一现象提示我们,由于高超声速飞行器表面不可避免地存在凹槽等结构,可以考虑通过凹槽外侧泄流的方式,卸除掉凹槽对下游的扰动.