局部分数阶积分下广义凸函数的Ostrowski型不等式
2020-02-18曾志红时统业田德路
曾志红, 时统业, 田德路
(1. 广东第二师范学院 a. 学报编辑部, b. 数学系, 广东 广州 510303;2. 海军指挥学院, 江苏 南京 211800)
设f:[a,b]→R在[a,b]上连续,在(a,b)上可微,且对任意x∈(a,b)有|f′(x)|≤M,则有
称式(1)为Ostrowski不等式[1].有关Ostrowski型不等式的结果可见文献[2-10].
近年来,分形理论在科学工程领域有非常广泛的应用.文献[11-12]系统地阐述了建立在分形空间上的局部分数阶微积分的相关理论.设Rα(0<α≤1)是分形实线的α型集合,aα,bα,cα∈Rα,则在这个分形集中有如下运算律:
1)aα+bα∈Rα,aαbα∈Rα;
2)aα+bα=bα+aα=(a+b)α=(b+a)α;
3)aα+(bα+cα)=(aα+bα)+cα;
4)aαbα=bαaα=(ab)α=(ba)α;
5)aα(bαcα)=(aαbα)cα;
6)aα(bα+cα)=aαbα+aαcα;
7)aα+0α=0α+aα=aα,aα1α=1αaα=aα.
下面使用Gao-Yang-Kang的方法来描述局部分数阶导数和局部分数阶积分.
1 预备知识
定义1[11-12]设f:R→Rα是不可微函数,如果对任意ε>0,存在δ>0,使得当|x-x0|<δ时,有|f(x)-f(x0)|<εα,则称f在点x0处局部分数阶连续.若f在区间I⊆R上局部分数阶连续,则记为f∈Cα(I).
定义2[11-12]设f∈Cα(a,b),则f在点x0处的α阶局部分数阶导数定义为
若对任意x∈I⊆R时存在f(α)(x),则记为f∈Dα(I).
定义3[11]设f∈Cα[a,b],则f在区间[a,b]上的α阶局部分数阶定积分定义为
式中:a=t0 引理1[11]对任意k∈R,有 在闭区间上局部分数阶连续的函数是局部分数阶可积的.局部分数阶定积分有与黎曼定积分类似的性质,如线性性质、区间可加性、比较性质、绝对不等式、牛顿-莱布尼茨公式、换元法、分部积分法等[12-13]. 引理2[13]设f(x)在[a,b]上连续,函数x=g(t)满足条件 1)g(c)=a,g(d)=b; 2)g(t)在[c,d]有连续α阶导数(0<α≤1),且值域Rg⊂[a,b],则有 文献[14]引入分形集上广义凸函数的概念. 定义4[14]设I⊆R,函数f:I→Rα,若对任意u,v∈I和任意λ∈[0,1],有 f(λu+(1-λ)v)≤λαf(u)+(1-λ)αf(v), 则称f是I上的广义凸函数. 文献[15-16]通过建立广义Montgomery恒等式,得到分形实线的分形集上的分数阶积分的广义Ostrowski型不等式.本文旨在建立新的局部分数阶积分下广义凸函数的Ostrowski型不等式.为得到本文的主要结果,我们需要下面的引理. 在引理3中, 取c=0,x=a, 得到文献[17]的定理1. 取c=b-a,x=a, 得到文献[17]的定理2. 文献[17]利用这2种特殊情况得到如下不等式: (2) (3) 式中:q≥1,a,b∈R,a (4) 证明 利用引理3得 由|f(α)|的广义凸性有 类似可得: 式中: 令b-t=u,利用引理2和引理1得: 类似可得: 综合式(8)~(12)得: (13) 式中: 类似可得: (16) 综合式(5)~(7)、(13)、(16),则式(4)得证. 推论1 设区间I⊆R,I°是I的内部,f:I°→Rα,a,b∈I°,a (17) 式中,P,Q分别如式(14),(15)所定义. 证明 由引理3和广义Hölder不等式得 式中, 用推导式(4)的方法得: 用推导式(13)的方法得 式中,P,Q分别如式(14),(15)所定义.综合式(21)~(27),则式(19)得证. 推论2 设区间I⊆R,I°是I的内部,f:I°→Rα,a,b∈I°,a 式中, 证明 在定理2中取x=a,c=0,则式(28)的第一个不等式得证.利用Hölder不等式可证式(28)的第二个不等式. 注1 式(28)是式(2)的加细. 推论3 设区间I⊆R,I°是I的内部,f:I°→Rα,a,b∈I°,a 式中, (29) 证明 在定理2中取x=a,c=b-a,则式(29)的第一个不等式得证.利用Hölder不等式可证式(29)的第二个不等式. 推论4 设区间I⊆R,I°是I的内部,f:I°→Rα,a,b∈I°,a 注2 式(30)是式(3)的加细. 文献[17]通过建立两个局部分数阶积分恒等式,得到分形集上的两个广义Hermite-Hadamard型不等式.本文利用将这两个恒等式统一起来的带有参数的局部分数阶积分恒等式,得到这两个广义Hermite-Hadamard型不等式的加细.

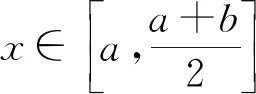

2 主要结果

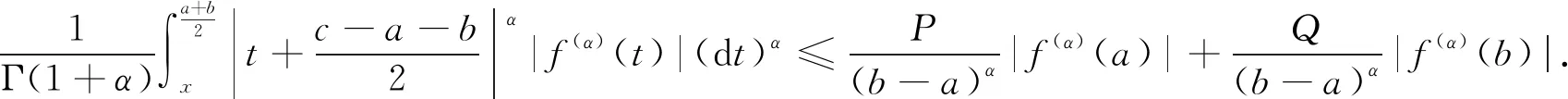
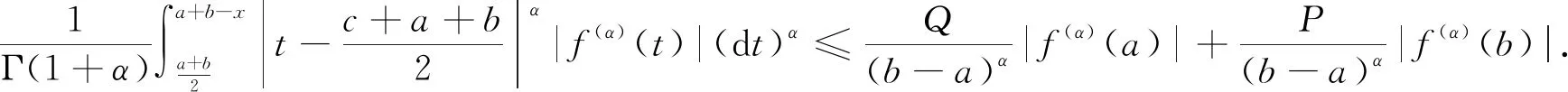


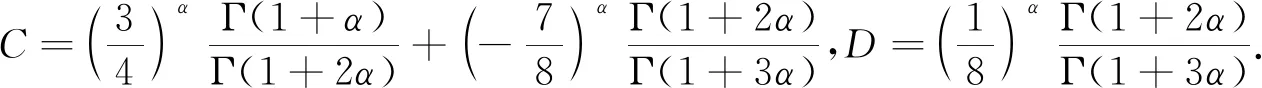
3 结 论
