水中目标自由场声辐射特性还原及远场声辐射热区识别

林伟，夏茂龙，刘正浩，黎胜，孟春霞

(1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连理工大学 船舶工程学院，辽宁 大连 116024；3.中国船舶及海洋工程设计研究院，上海 200011；4.水下测控技术重点实验室，辽宁 大连 116013)

0 引言

21世纪被称为海洋的世纪，随着人类对海洋探测活动的日益增多，水中目标的快速探测和精确识别成为现代国防与海洋工程领域研究的热点[1]。水中目标声场信号传播距离远[2]、信息保真性好，是水中目标识别的主要信息来源[3]，因此准确获取水中目标声特性尤为重要。获取水中目标特性的理想测量条件是水下自由场，在水下自由场中测量得到的目标声特性没有边界及其他噪声源如海洋生物和舰艇船舶等的干扰，是目标自身不受环境影响的特性。因此获取水中目标在水下自由场中的声特性对目标识别和控制具有重要意义。虽然自然界中不存在完全的自由场，但是通常情况下海洋和大的湖泊等开阔海域可以近似为水下自由场，然而天然试验场地受天气条件和水中生物等影响大而且测试费用高昂；室内消声水池是人工制造的、比较理想的水下自由场，但不适用于大型水下结构而且在低频测量时不满足自由声场条件[4]。另一方面，对于水下目标特别是潜艇等薄壳结构，结构振动时在表面产生的倏逝波会对结构声辐射热区的定位造成明显干扰。倏逝波是沿结构表面传播、沿结构表面法向指数衰减的波，直接使用法向声强方法定位的辐射热区受倏逝波的影响，无法准确定位出传播到远场的声辐射热点区域，也就无法控制目标的远场声特性。因此如何实现在非自由场近场条件下获得水中目标自由场声特性和识别传播到远场的声辐射热区，具有一定的理论研究和工程实际价值。

面对自由场条件难以满足的问题，很多学者提出了不同的解决方法。针对近场声全息(NAH)技术[5-10]识别目标时容易受到边界和外部噪声源的干扰问题，Williams等[11]提出了基于空间傅里叶变换的声场分离技术，但该声场分离技术只能用于平面、柱面、球面等规则声源和测量面，对于不规则形状无法进行分离。Bi等[12]提出基于等效源法的声场分离技术，该技术与近场声全息技术结合，实现了不规则测量面上声场的分离。田湘林等[13]、王晓东[14]分别研究了基于等效源法的单全息面声场分离技术。周思同等[15]提出基于简正波和波叠加法的水下非自由声场重建技术。Bobrovnitskii等[16]提出基于球谐波分解和转换矩阵获取声源特性的方法，该方法能快速预测声源的声功率，但不能给出近场声压信息。Langrenne等[17]提出利用边界元法在复杂声场中获取目标自由场特性的方法，该方法基于边界元法，适用于任意三维复杂结构，而且具有明确的推导过程，能够在复杂声场环境中准确还原目标的自由场声特性。因此将基于边界元的声场还原方法用于解决水中目标自由场测量条件难以实现的问题，能够实现在非自由环境下获取水中三维目标的自由场声特性[18]。

虽然利用声场还原技术能够消除边界和外部噪声源的干扰，但当非自由环境下获取目标的自由场声特性是在近场时，受倏逝波的影响，在目标结构表面会形成一部分能量流，这部分能量流不能传播到远处而是在振动结构表面进出循环[19]，影响对目标结构远场声辐射热区的定位，进而影响对目标远场声特性的控制。为准确定位传播到远场的声辐射热区，很多学者提出了不同的方法。Williams[20-21]最早提出超声速声强的概念，将声场信息转换到波数域中，过滤掉倏逝波的部分，进而只得到传播波的部分，称为超声速声强。但是该理论只适应于简单结构，不适合实际工程应用。因此Junior等[22]提出有用声强的方法确定远场辐射热区，该方法利用赫姆霍兹积分方程求出结构的声辐射阻抗矩阵，对声辐射阻抗矩阵进行奇异值分解，过滤掉小的奇异值所对应的振动结构表面速度分布模式，就能够获得任意形状结构的超声速声强。虽然该方法适应于任意形状结构，但是这种方法存在奇异值的选取问题。Marburg等[23]提出声辐射表面贡献方法，该方法同样是基于赫姆霍兹积分方程，首先利用结构表面声压和法向速度的关系求出声阻抗矩阵，然后进一步求出声辐射模态矩阵，最后设定一个正值，求出声功率的表面贡献向量。该方法适合任意的三维复杂结构，不存在过滤较小奇异值的问题。表面贡献法通过板模型的验证，能够有效去除倏逝波干扰。Barnard等[24]提出混响环境中的超声速声强(SIRE)技术，利用水下矢量传感器获取混响环境中目标的窄带声功率和指向性。但该方法在声场分离时没有考虑向内声场作用在声源表面产生的散射影响，并没有得到自由场特性。

本文针对水下近场非自由场环境中获取水中目标的自由场声特性和识别远场声辐射热区难以实现的问题，提出结合基于边界元法的声场还原技术和表面贡献法，在边界和外部噪声源影响下获取水中目标的自由场声特性，同时在近场分离倏逝波得到能够辐射到远场的声强分布云图。该方法将突破测试环境对水中目标声特性测量的限制，提高目标声特性的测量能力和水平，大幅降低测试费用，具有广泛的工程应用价值。

1 声场还原方法和表面贡献法理论基础

1.1 水中声场分离

复杂环境中测量面处场点的总声场可以分为指向声源方向的向内传播声场和背离声源方向的向外辐射声场，向内传播声场是由外边界反射和外部声源向内辐射造成的，向外辐射声场则由声源的自由场辐射声场和向内的声场入射在声源表面形成的散射声场组成。

图1所示为复杂声场环境中的目标声源和测量面示意图。图1中：Γ1表示所求的声源S0的表面；Γ2表示声场边界；S表示测量面；V1和V2表示S将边界Γ1和边界Γ2之间空间分开的两部分，V=V1+V2；nΓ1和nΓ2分别表示Γ1的法向和Γ2的法向；nS表示测量面S的法向；s′表示测量面上的点；Q(r′)表示r′处的外部声源，r′表示外部声源所在的位置。

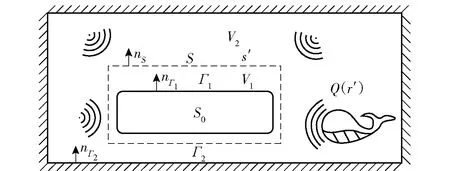
图1 复杂声场环境中的目标声源和测量面示意图

当r∈Vi，i=1，2时，根据赫姆霍兹积分方程，空间中任意一点的声压可以表示[25]为

(1)

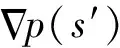
(2)

i为虚数单位，k为波数。

对于内场问题，(1)式可以简化为

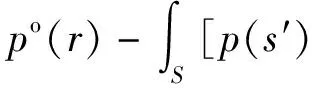
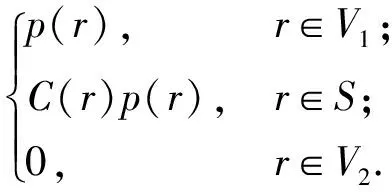
(3)

式中：po(r)表示向外声压，上角标o表示声压方向向外；∂nG(r,s′)表示格林函数对法向的偏导数；ρ0表示声场中流体密度；ω为圆频率；vn(s′)为s′处法向速度；C(r)为r处的系数，

(4)

已知S积分面上的声压和声压梯度时，向外声压可以根据(3)式求出：

po(r)=C(s′)p(s′)+

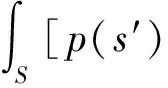
(5)

式中：C(s′)为s′处的系数。

散射声场由向内声场作用在声源表面产生，因此需要先计算作用在Γ1上的入射波，再计算散射场。向内声场由外部边界反射和外部噪声源两部分组成，当考虑外场问题时，向内声压在(1)式中可以表达为

pi(r)+

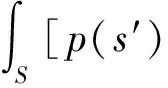
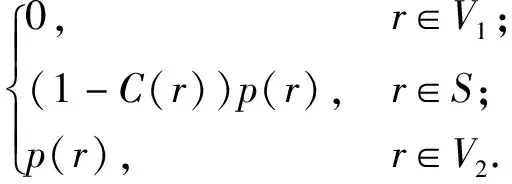
(6)

根据(6)式，当r∈V1时作用在声源表面的入射声压pi(r)表示为

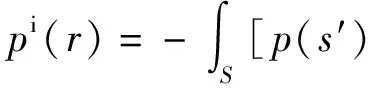
iρ0ωvn(s′)G(r,s′)]dS.

(7)

计算散射声场时，假设声源S0是静止的，同时结构是刚性的，因此∂nΓ1p(r)=0.对于Γ1表面的外场问题可以表示[26]为

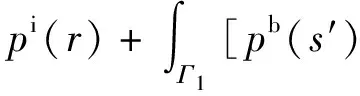
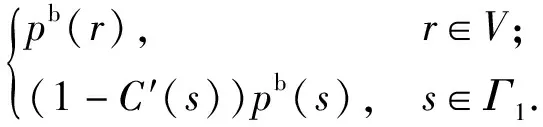
(8)

式中：pb(s)为s处向内声场作用在声源表面散射形成的声压；pb(r)为r处向内声场作用在声源表面散射形成的声压；C′(s)为s处的系数。在声源表面为刚性的假设下，考虑声源辐射问题，从声源表面辐射到中间测量面S上的散射声压psc(r)可以表示为

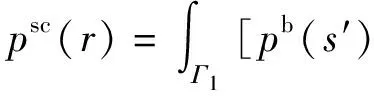
(9)

式中：pb(s′)为s′处向内声场作用在声源表面散射形成的声压。结合(5)式、(7)式、(8)式、(9)式，可以得出

(10)

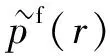
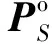
(11)

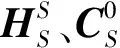
(12)

根据(8)式将边界离散后，散射声压可以表示为

(13)

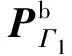
运用边界元法会遇到解不唯一的情况时，可以利用CHIEF点法[27-28]克服这一缺陷。根据(9)式将边界进行离散，测量面S上的散射声压可以表示为

(14)

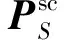
在实际应用中，使用基于边界元的声场还原技术需要在声源周围布置测点，测点形成的包络面称为测量面，声源必须在测点形成的包络面内；通过测量获取测量面上测点声压和法向振速，结合赫姆霍兹积分方程求出测点处向内传播和向外辐射的声压；利用入射到声源表面的向内声压求出散射声压，再由向外声压减去散射声压，即为目标声源的自由场辐射声压。

1.2 水中倏逝波滤波

表面贡献方法是基于赫姆霍兹方程，因此该方法适用于具有任意三维形状的结构，具有一定的工程应用价值。利用赫姆霍兹积分方程，将结构表面离散后可以将结构表面声压表示为

HP=Gvn，

(15)

式中：P为表面节点处声压；vn为表面节点处法向振速；H和G为边界元系数矩阵。

结构的辐射声功率W可以表示为

(16)

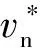
将结构表面进行离散，结合(15)式、(16)式得出结构的辐射声功率为

(17)

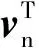
(18)

Φ为插值函数向量。

定义声功率表面贡献量为η，总的辐射声功率可以通过对边界表面的积分得到，即

(19)

式中：β(x,y,z)无物理意义；β*(x,y,z)为β(x,y,z)的共轭，二者的乘积使η恒为正值。

结构表面边界离散后，辐射声功率可以表示为

(20)

结构的声辐射模态与结构的声阻抗矩阵和边界质量矩阵有关，它们存在如下关系：

ZRΨ=λAΨ，

(21)

式中：Ψ为声辐射模态矩阵，Ψ有如下特性：

I=ΨTAΨ，

(22)

根据Ψ的特性，可以得到

ξ=ΨTAvn；

(23)

λ为一对角阵的特征值，对角阵Λ为

Λ=ΨTZΨ.

(24)

用声辐射模态叠加可以得到结构表面的节点速度，表示为

vn=Ψξ，

(25)

式中：ξ为声辐射模态贡献因子向量。

(22)式、(25)式代入(17)式，得到

(26)

由(20)式、(23)式可知：

(27)

当β已知时就可以求η，进而通过对声功率表面贡献η的积分，可以求出总的声功率。

综上所述，表面贡献法是基于赫姆霍兹积分方程，利用结构表面声压和法向速度的关系，求出声阻抗矩阵，然后进一步求出声辐射模态，设定一个正值，求出声功率的表面贡献向量。

2 数值计算及讨论

2.1 模型的建立

声源是1个振动的两端简支圆柱壳，其各项参数如表1所示。

表1 圆柱壳参数

圆柱壳中心处在原点，轴向平行于y轴，在垂直于x轴1 m、z轴-1 m处，分别设置一个刚性面模拟外部边界，在位于(0 m，0 m，2 m)处设置1个强度为100 kg/s2单极子源模拟外部噪声源。测量面为1个圆柱面，该圆柱面以原点为中心，轴向平行于y轴，长5 m，半径0.795 77 m，用b表示圆柱壳长；在(0 m，0 m，-0.7 m)处施加1个z轴方向1 N的力。流体介质为水，水中声速为1 500 m/s，密度为1 000 kg/m3.本文旨在研究声场分离的准确性，要求水下结构在自由场中和复杂环境下相同激励下的振动辐射噪声，具体做法是：1)当结构位于自由场中时，先使用商用有限元程序仅对结构进行有限元离散，计算结构在点力激励下的振动响应，再将有限元分析得到的结构振动响应输入商用边界元程序，获得其自由场特性；2)在有外部噪声源和外部边界情况下，同理先使用商用有限元程序仅对结构进行有限元离散，计算结构在点力激励下的振动响应，再将有限元分析得到的结构振动响应输入商用边界元程序中，同时在程序中设置外部噪声源和外部边界，获取其在复杂声场中的特性。数值仿真模型如图2所示。

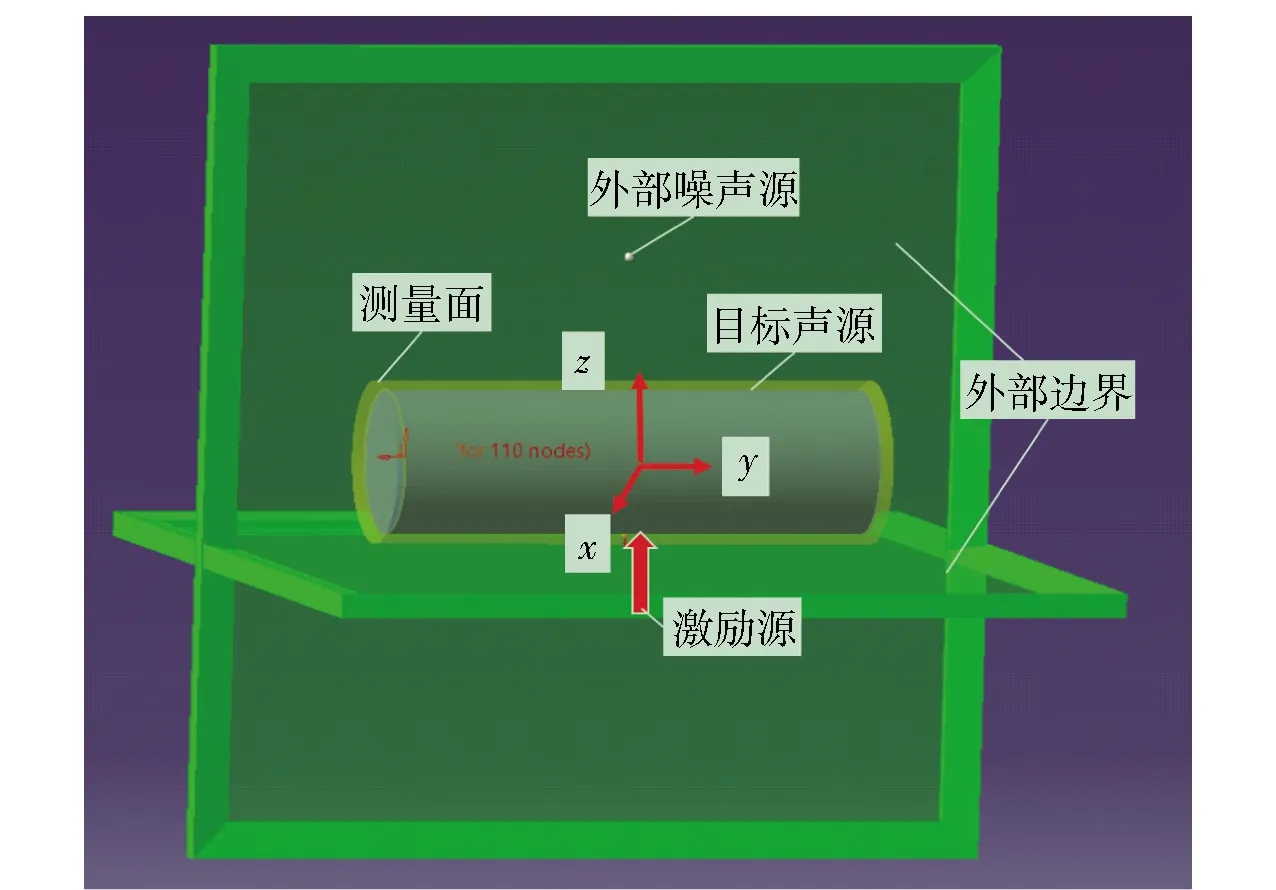
图2 数值仿真模型

2.2 自由场声场还原

利用边界元和有限元耦合的方法，获取点力激励下振动圆柱壳在以刚性边界为界的半空间中存在点声源干扰的声场分布。通过复杂声场中测量面上的声压和法向振速，代入(3)式，求出测量面上的向外声压；将(7)式、(8)式代入(9)式，求出测量面上向内声压作用在声源表面的散射声压；利用(10)式向外声场减去散射声压，还原得到目标自由场声压特性。

首先，比较声强的还原效果，声强计算公式如下：

(28)

式中：pe(s)为计算声功率选定的声压，例如计算自由场声功率时pe(s)等于自由场声压pf(s)；c为流体介质中的声速。

分别将复杂声场中测量面上直接测量得到的声压定义为总声场声压、测量面上背离声源方向的声压定义为向外声场声压、指向声源方向的声压定义为向内声场声压、经过声场还原技术得到的声压定义为还原声场声压、自由场中得到的声压为自由场声压，测量面上自由场、总声场、向外声场、还原声场的声功率级，结果如图3所示。

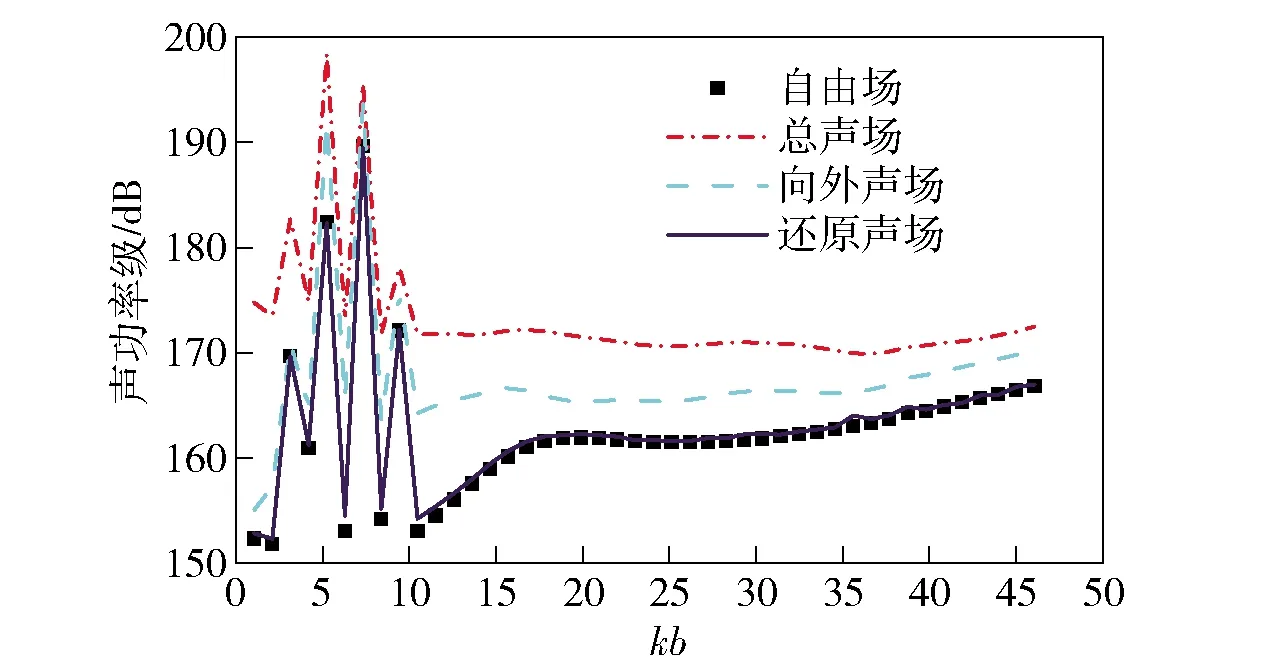
图3 各声场声功率级

图3中横坐标k为波数、b为测量面轴向长度，纵坐标为声功率级(参考声功率级10-18W)。由图3可见，边界和外部噪声源对目标声场影响较大，很难直接获取目标的自由场特性。向外声场的声功率和自由场声功率也有较大差别，表示声场在外部边界和噪声源的作用下，散射声场不能忽略。向外声场消除散射声场影响后得到的还原声场声功率和自由场声功率基本一致，误差小于1 dB.

其次，比较总声场和还原声场与自由声场的场点声压相对平方误差，相对平方误差的计算公式如下：

(29)

从图4中可以发现，边界和外部干扰源使总声场场点声压和声源自由场场点声压的相对平方误差在70%以上，最高值达到590%，这意味着声场边界和外部噪声源对目标声场有很强的干扰；而通过基于边界元的自由场还原技术获取的目标还原声场与自由声场相对误差除个别点外均保持在30%左右，表明该技术，能够很好地消除外部边界和噪声源的干扰、获取目标自由场特性。

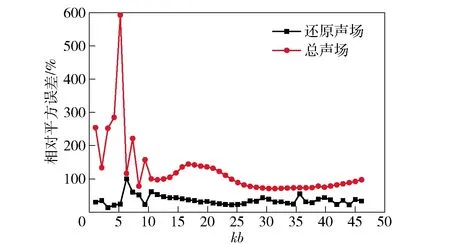
图4 总声场和还原声场相对自由场的相对平方误差

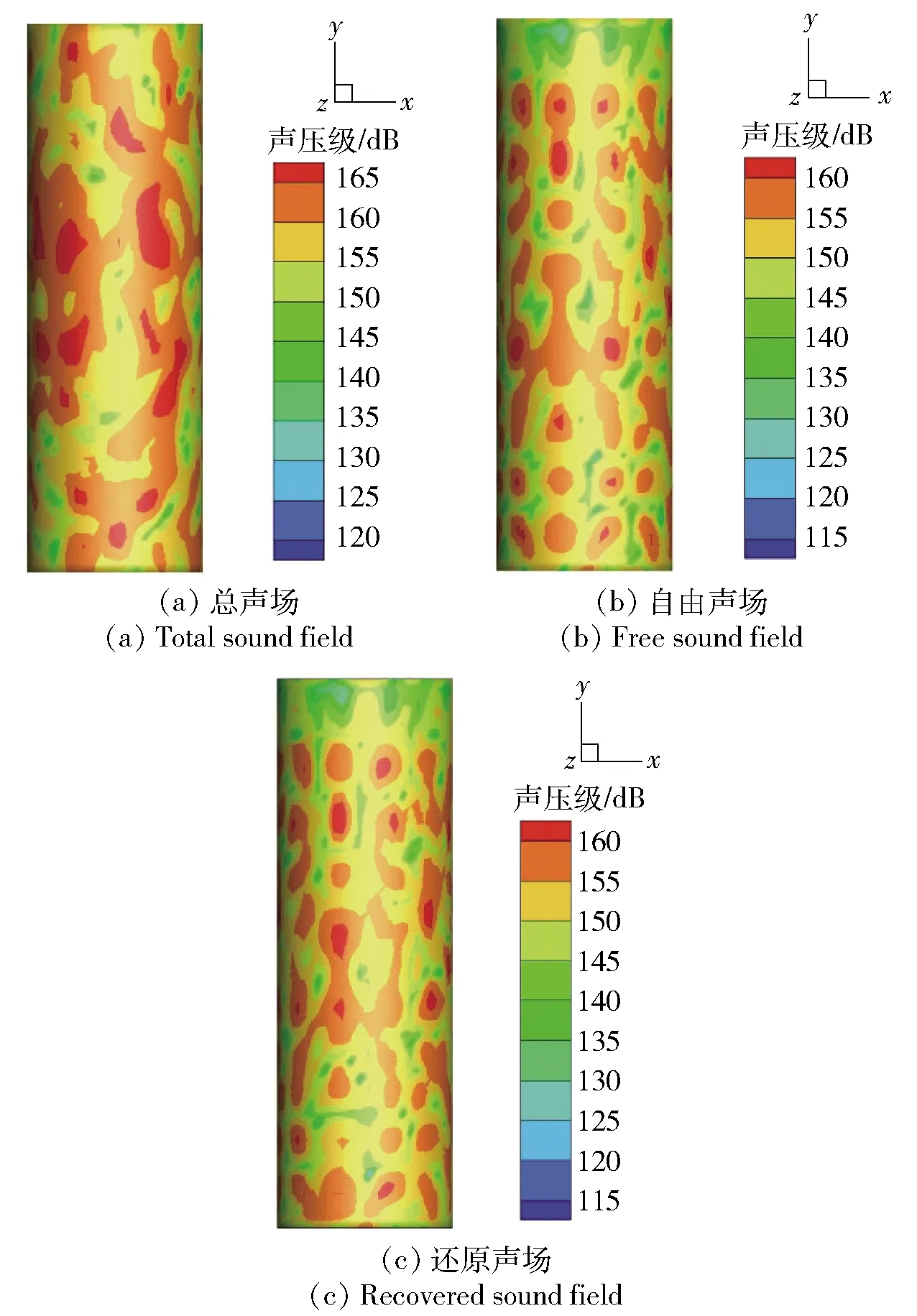
图5 2 200 Hz声场场点声压分布云图

最后，为验证还原后声场场点声压分布情况，比较总声场、还原声场和自由场场点声压分布云图。图5(a)、图5(b)、图5(c)分别给出了2 200 Hz下总声场、还原声场和自由声场的场点声压分布云图对比以及计算结果。通过对比图5(a)和图5(b)可知，获取目标自由场特性需要进行声场还原，以消除外部边界和噪声源干扰；图5(b)和图5(c)的结果验证了还原声场与自由声场热点区域基本一致。综上所述，通过对比还原声场和自由声场的声功率、声压和场点声压分布等声场特性发现：利用基于边界元的声场还原技术能够在非自由环境中获取目标的自由场声辐射特性。

2.3 倏逝波滤波

由于声源特性是在近场测量获取的，还原后的声场包含倏逝波的信息，为了获取传播到远场的声场信息，需要对倏逝波进行滤波[29]。由于测量面是三维圆柱壳，而表面贡献法能够有效消除具有复杂几何形状的三维结构表面的倏逝波干扰，因此采用表面贡献法消除圆柱壳表面的倏逝波干扰，获取传播到远场的声辐射热区。

图6(a)所示为2 200 Hz时测量面上还原声场的法向声强，图6(b)所示为2 200 Hz时测量面上还原后的声场信息利用表面贡献法得到传播到远场的声强分布云图。对比图6(a)、图6(b)可以发现：图6(a)表面声强有正有负，代表了近场声场和结构的能量交换，由包含这一能量流的表面声强所标示的声辐射也弥散于圆柱壳表面；图6(b)中的声强均为正值，声强数值大小表示了对应面积对声能量的贡献量。表面贡献法过滤掉循环于振动结构表面的能量流，只留下对声能量的净贡献，标示的声辐射热区也更集中。因此在近场测量时需要进行倏逝波滤波，从而判断声源辐射到远场的热点区域，为后期研究提供基础。

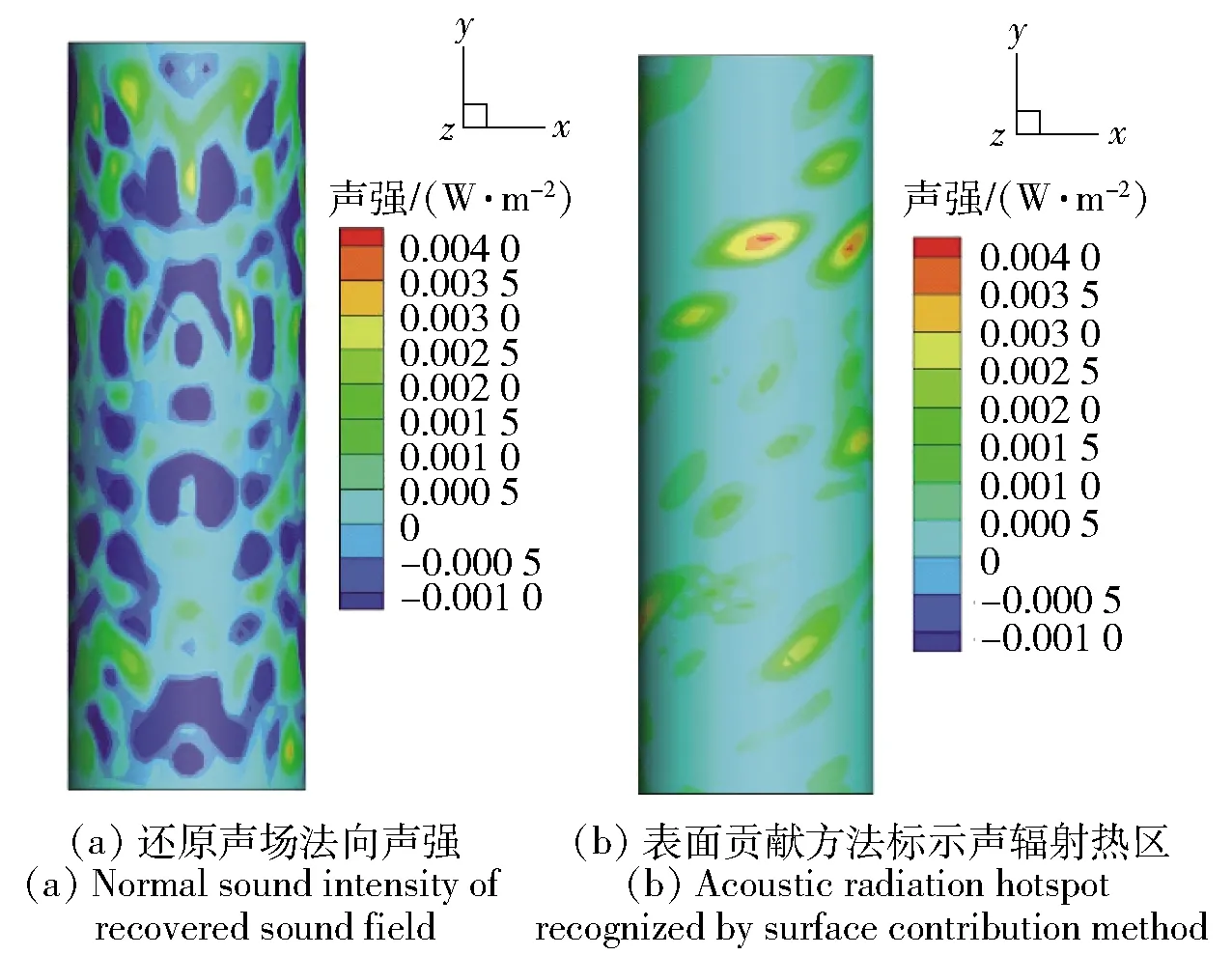
图6 2 200 Hz 声强分布云图

3 结论

本文提出了结合基于边界元的声场还原方法和表面贡献法的声场分离技术，实现了近场非自由情况下获取目标自由场特性，同时在近场区域识别对远场辐射有贡献的热点区域，并利用水下圆柱壳模型进行数值验证。根据数值仿真结果发现，外部边界和噪声源会严重干扰目标声源特性的测量，而基于边界元的声场还原技术能够有效还原目标声源在非自由场的自由场声场特性。还原的声场特性与在自由场中直接计算获取的目标声源声场特性如声功率、场点声压等相差不到1 dB，场点声压的相对平方误差很小，场点声压分布云图也基本一致。而利用表面贡献法可以在近场区域有效识别出对远场声辐射有贡献的热点区域，由于消除了倏逝波干扰，只留下对声能量的净贡献，标示的声辐射热区也更为集中，为目标控制提供基础。因此利用结合基于边界元的声场还原技术和表面贡献法的声场分离技术，可以突破测量实验环境对水中目标声特性测量的限制，在近场非自由条件下获取目标自由场特性并在近场识别辐射到远场的热点区域，极大地提高目标特性的测量能力和水平，为控制目标辐射特性提供依据，具备一定的工程应用前景。