基于可观测性分析的混合式惯性导航系统连续自标定模型选择
2020-02-18王琪汪立新梁树晖秦伟伟沈强
王琪,汪立新,梁树晖,秦伟伟,沈强
(1.火箭军工程大学 导弹工程学院,陕西 西安 710025;2.96901部队 22分队,北京 100089;3.火箭军工程大学 核工程学院,陕西 西安 710025)
0 引言
混合式惯性导航系统是一种新型惯性导航系统,它吸收了平台式和捷联式惯性导航系统的各自优点,并将隔离载体角运动的物理平台、捷联姿态算法与旋转调制抑制误差效应三者集于一体。该系统主要着眼于高速和高动态运载器对高精度惯性导航提出的新需求,不仅能大幅度提高导航定位精度、实现快速精确自对准,还可实现装机条件下的自标定,明显降低购置和维护成本[1]。
惯性系统误差标定补偿是提高系统精度的有效手段,考虑到传统多位置自标定对于惯性仪表(陀螺仪和加速度计)安装误差系数标定精度低的缺点[2-3],并针对混合式惯性导航系统三轴全姿态物理平台和系统装机自标定的特点,选择运用连续自标定方法[4]进行混合式惯性导航系统的误差自标定。
连续自标定方法的基本原理如下:物理平台在外力矩的作用下以角速度ωc(称为加矩角速度)转动,在地球自转角速度、加矩角速度以及重力加速度的激励下,加速度计输出中包含有陀螺仪误差、加速度计误差、安装误差和平台对准误差等全部误差信息。以加速度计输出为观测量,以平台对准误差方程建立动力学模型,采用最优滤波算法就可以估计平台误差系数和对准误差[5]。连续自标定方法自提出以来,已经在国外得到了广泛应用,而国内由于缺乏全姿态平台,该方法并未引起广泛重视,研究相对较少。杨华波[6]首次系统介绍了连续自标定的相关内容;文献[7-8]针对传统失准角误差模型不适用于大失准角情况的问题,建立了框架角误差模型;文献[9-10]为提高安装误差的可观测性,分别以加速度计输入轴和陀螺仪输入轴为基准平台坐标系建立了标定模型,提高了安装误差的标定精度。
混合式惯性导航系统在地面标定时处于稳定和稳定加旋转两种工作模式[1],此时混合式惯性导航系统的工作原理与平台式惯性导航系统相同,因此可以采用平台式惯性导航系统的失准角方程和框架角方程作为动力学方程建立自标定模型,观测方程主要是加速度计输出方程和平台框架角传感器输出方程,而且在不同坐标系定义下会有不同的系统模型形式。本文从系统方程可观测性分析出发,考虑到使用连续自标定方法的主要目的之一是提高惯性仪表安装误差系数的标定精度,将分析不同系统模型中惯性仪表安装误差的可观测性,以此研究不同系统模型适用的条件,作为系统模型选择的依据。
1 混合式惯性导航系统连续自标定模型
1.1 坐标系定义
混合式惯性导航系统主体是三框架结构物理平台,由3个光纤陀螺仪与3个石英挠性加速度计组成。定义如下坐标系:
1)地理坐标系(n):地理坐标系采用当地东- 北- 天坐标系,原点为平台中心,Xn轴指向正东,Yn轴指向正北,Zn轴指向与地球表面垂直向上的方向,并与Xn、Yn轴构成右手正交坐标系。
2)以平台六面体为基准定义的平台坐标系(ps):以平台六面体3个正交轴为基准,Xps、Zps为平台的水平轴,Yps为平台的方位轴,三轴构成右手正交坐标系,坐标原点为平台台体的几何中心;在不存在安装误差的情况下,Xps轴、Yps轴和Zps轴分别与3个陀螺仪的敏感轴平行。
3)以加速度计输入轴为基准定义的平台坐标系(pa):以平台几何中心为原点,Xpa轴与X轴加速度计敏感轴平行,Ypa轴平行于X轴和Y轴加速度计敏感轴所确定的平面,并与Xpa轴垂直,Zpa轴与Xpa轴以及Ypa轴构成右手正交坐标系,X、Y、Z为平台的3个框架轴。
4)陀螺仪敏感轴坐标系(gI):XgI轴、YgI轴和ZgI轴分别与X轴陀螺仪、Y轴陀螺仪和Z轴陀螺仪的敏感轴平行;由于陀螺仪存在安装误差,该坐标系为非正交坐标系。
5)加速度计敏感轴坐标系(aI):XaI轴、YaI轴和ZaI轴分别与X轴加速度计、Y轴加速度计和Z轴加速度计的敏感轴平行;由于加速度计存在安装误差,该坐标系为非正交坐标系。

(1)

设平台按照Z-X-Y框架轴的顺序转动,则c系与n系之间的转换矩阵为

(2)
式中:θx、θy、θz分别为平台绕X、Y、Z框架轴转动的角度。
1.2 惯性仪表安装误差
根据定义,惯性仪表敏感轴坐标系(gI系和aI系)是非正交坐标系,因此从gI系和aI系到p系的转换矩阵由正交化矩阵和转动矩阵[11]两部分组成。
正交化是指将非正交的gI系和aI系变为正交系的过程。定义正交化后的坐标系X轴与惯性仪表的X敏感轴平行,Y敏感轴与正交化坐标系的OXY平面平行。由于所有仪表安装误差角均满足小角度假设,gI系和aI系的正交化矩阵Ta与Tg可表示为
(3)

转动是指将正交化后gI系和aI系转至与p系重合的过程。设从正交化后的gI系和aI系到p系的转动矩阵为M(ΔM)和M(ηM),则惯性仪表安装误差矩阵为
(4)
式中:ΔM和ηM为陀螺仪和加速度计经正交化后的gI系和aI系到p系的误差角,同样假设其满足小角度假设。根据p系定义的不同(ps系或pa系),(4)式中的矩阵M(ΔM)和M(ηM)有不同的表达式,进而引起仪表安装误差矩阵存在不同形式。
1.2.1 平台坐标系为ps系
当以平台六面体为基准定义p系时,矩阵M(ΔM)和M(ηM)为
(5)
将(5)式代入(4)式并忽略小角度乘积,可得
(6)
从(6)式中可以看出,当定义平台坐标系为ps系时,陀螺仪和加速度计各存在6项安装误差角。
1.2.2 平台坐标系为pa系
根据pa系的定义,当以加速度计输入轴为基准定义p系时,矩阵M(ΔM)和M(ηM)为
(7)
将(7)式代入(4)式并忽略小角度乘积,可得
(8)
从(8)式中可以看出,当定义平台坐标系为pa系时,陀螺仪有6项安装误差角,而加速度计只有3项安装误差角。
1.3 系统模型
混合式惯性导航系统连续自标定系统的系统动力学方程有失准角方程和框架角方程,观测量有加速度计输出和平台框架角传感器输出。而在不同的平台坐标系定义下,这些方程有不同的表达形式,因此可以构建不同的系统模型。为简化分析,假设陀螺仪和加速度计的误差系数已经事先补偿,在方程中没有体现。
1.3.1 系统动力学方程
平台失准角方程[4]为
(9)
式中:ωc为施加在平台框架上的加矩角速度。
平台框架角方程[5]为
(10)
1.3.2 观测方程
混合式惯性导航系统连续自标定中的观测量有加速度计输出和平台框架角传感器输出,其中框架角传感器的输出就是平台框架角的真实值,观测方程可以写为
(11)
式中:Zs为框架角传感器的输出。
在不考虑加速度计误差系数的情况下,加速度计输出模型为
(12)
式中:Za为加速度计输出;gp为地球重力加速度在平台坐标系的投影,根据系统动力学方程选择的不同,gp有不同的表达形式。
1.3.3 连续自标定模型
根据上述系统动力学方程和观测方程,可以构建不同的系统模型如下:
1)系统模型1.以失准角方程为动力学方程、加速度计输出方程为观测方程:
(13)

2)系统模型2.以框架角方程为动力学方程、加速度计输出方程为观测方程:
(14)
在以框架角方程为动力学方程时,由于框架角中包含了失准角,p系和c系之间的转换矩阵无法单独写出,都包含在n系和p系之间的转换矩阵中,并且有
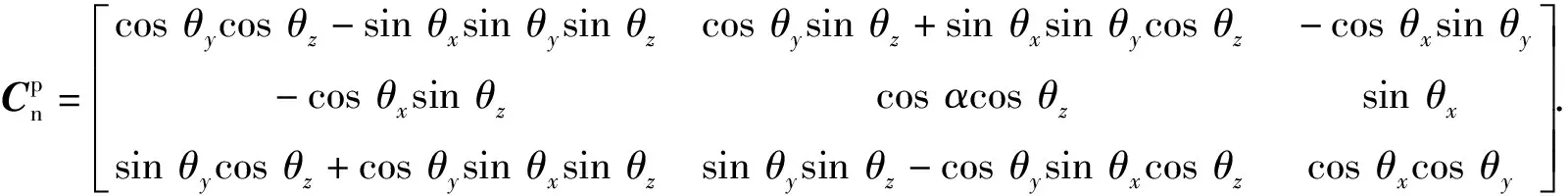
(15)
3)系统模型3.以框架角方程为动力学方程、加速度计输出方程和平台框架角传感器输出方程为观测方程:
(16)
在利用失准角方程建立系统模型时,在(1)式中对失准角φ进行了小角度假设,因此以失准角方程为动力学方程建立的自标定模型只适用于小失准角的情形。而以框架角方程为动力学方程建立的自标定模型不存在失准角的小角度假设,可以适用于大失准角模型。
2 系统模型可观测性分析
对于动态系统,影响系统状态量可观测性的主要因素有两方面:一是系统输入。对于连续自标定系统,系统输入主要受标定方案的影响,不同的标定方案使得惯性仪表三轴上敏感的加矩角速度、地球自转角速度和地球重力加速度的分量不同,从而激励不同的状态量并影响状态量的可观测性。因此可以通过设计最优的标定方案来尽可能激励所有状态量。二是系统的结构特性。与系统输入不同,系统的结构特性对其状态量可观测与否的判断是决定性的,即对于确定的系统模型,系统状态量可观测与否也是确定的,无法通过改变系统输入使不可观测的状态量变得可观测。从系统结构特性的角度判断状态量是否可观测,主要是看该状态量能否独立表现在系统量测或其各阶导数中。
根据可观测性的定义,状态量可观测意味着根据系统输入与观测量可以唯一确定该状态量,即若状态量可观测,观测量或其各阶导数中必然包含该状态量的独立分量。而且由于任何系统都存在一定的干扰,如系统观测量的随机噪声和系统观测模型与真实模型之间的偏差等,对观测量的求导会将观测量中的噪声放大、降低信噪比,进而导致状态量估计所需的观测时间变长,估计精度受观测误差的影响也更大。因此,包含独立状态量的观测量求导阶数越高,该状态量的可观测性越低,体现在估计速度越慢、估计精度越低[12]。
根据上述分析,分别对3种系统模型在ps和pa坐标系下陀螺仪和加速度计安装误差的可观测性进行分析,作为最终选择系统模型的依据。
2.1 系统模型1
2.1.1 平台坐标系为ps系
由于安装误差角满足小角度假设,有
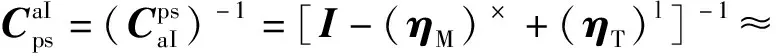
I+(ηM)×-(ηT)l.
(17)
将(6)式和(17)式代入(13)式,可得
(18)
对于向量a和b,其反对称矩阵及由其构成的上三角矩阵有如下性质:
(19)
则(18)式可以分别改写为
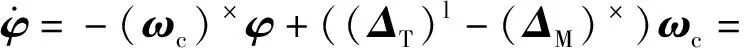
-(ωc)×φ+(ωc)lΔT+(ωc)×ΔM,
(20)
Z=[I+(ηM)×-(ηT)l](I-φ×)gc=
gc-φ×gc+(ηM)×gc-(ηM)×φ×gc-
(ηT)lgc+(ηT)lφ×gc=
gc+(gc)×φ-(gc)×ηM-(gc)lηT+
(ηM)×(gc)×φ-(ηT)l(gc)×φ.
(21)
从(21)式可以看出,在观测量Z中,加速度计安装误差ηT、ηM都存在独立分量,因此是可观测的。而陀螺仪安装误差ΔT、ΔM不存在独立分量,因此对观测量Z求1阶导数并将(20)式代入,可得

(gc)×[-(ωc)×φ+(ωc)lΔT+(ωc)×ΔM]+
[(ηM)×(gc)×-(ηT)l(gc)×]·
[-(ωc)×φ+(ωc)lΔT+(ωc)×ΔM]=
-(gc)×(ωc)×φ+(gc)×(ωc)lΔT+
(gc)×(ωc)×ΔM+[(ηM)×(gc)×-(ηT)l(gc)×]·
[-(ωc)×φ+(ωc)lΔT+(ωc)×ΔM].
(22)
从(22)式可以看出,在观测量Z的1阶导数中,陀螺仪安装误差ΔT、ΔM存在独立分量,因此是可观测的。因此,系统模型1在ps系下是可观测的,并且加速度计安装误差的可观测性优于陀螺仪安装误差。
2.1.2 平台坐标系为pa系
与(17)式同理,有
(23)
将(8)式和(23)式代入(13)式,并根据(19)式可得
(24)


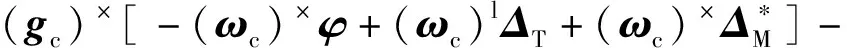
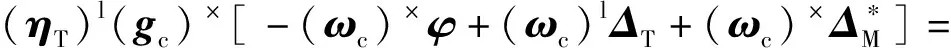
-(gc)×(ωc)×φ+(gc)×(ωc)lΔT+


(25)

综上所述,系统模型1在ps系和pa系下都是可观测的,且加速度计安装误差的可观测性优于陀螺仪安装误差。考虑到在pa系下的加速度计安装误差要小于ps系下的,因此在使用系统模型1时,选择以加速度计输入轴为基准定义的平台坐标系,即ps系。
2.2 系统模型2
在平台工作时,由于力矩反馈电路的存在,如果要令平台各框架转动,则需要通过陀螺仪对平台各框架轴上的力矩电机输入相应的力矩电流,通过力矩电机驱动平台各框架转动。而在安装时,陀螺仪与平台框架都是以平台六面体为基准的,因此在选择平台框架角方程时,平台坐标系必须以平台六面体为基准进行定义,此时系统模型为
(26)
将(6)式和(17)式代入(26)式,并根据(19)式可得
(27)

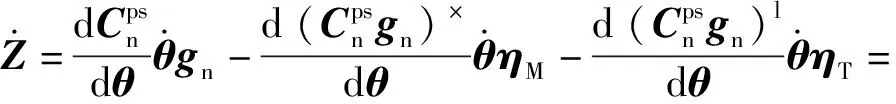
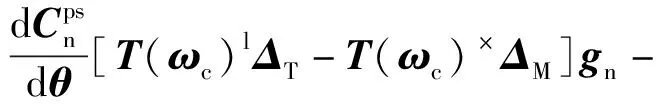



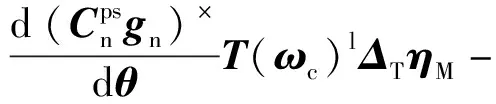


(28)
在(28)式中可以看出,陀螺仪安装误差ΔT、ΔM也不存在独立分量,而且如果再进一步对Z进行求导也不会存在独立分量,因此在系统模型2中,加速度计安装误差可观测,而陀螺仪安装误差不完全可观测。
2.3 系统模型3
同系统模型2,在选择系统模型3时平台坐标系必须以平台六面体为基准进行定义,此时系统模型为
(29)

(30)

从(29)式和(30)式可以看出,陀螺仪安装误差ΔT、ΔM和加速度计安装误差ηT、ηM分别在观测量Z及其1阶导数中存在独立分量,因此系统模型3可观测,且加速度计安装误差的可观测性优于陀螺仪安装误差。需要注意的是,在(30)式中,激励陀螺仪安装误差ΔT、ΔM的输入激励为平台加矩角速度ωc,为激励所有的6个陀螺仪安装误差,要求ωc的3个分量都有输入,因此要求惯性导航系统的3个框架轴都可以全方位转动,传统的平台式惯性导航系统无法做到这一点,而混合式惯性导航可以。
3 仿真分析
为验证以上可观测性分析结果,对3个系统模型分别进行仿真,其中系统模型1的非线性程度较低,采用扩展卡尔曼滤波算法;而系统模型2和3的非线性程度较高,采用无迹卡尔曼滤波算法。首先设置仿真初始条件[13]如下:
1)在连续自标定开始之前,平台处于空间稳定的工作状态,即始终跟踪当地水平面;
2)滤波周期T=0.2 s;
3)陀螺仪量测噪声标准差为0.001°/h;
4)加速度计量测噪声标准差为1×10-6m/s2;
5)平台框架角传感器量测噪声标准差为0.001°;
6)滤波初值设置为0.
由于惯性仪表安装误差的量值相对较小,定义如下相对误差来表示误差系数的标定精度:
(31)
文献[14]表明,平台应该至少绕2个框架轴转动2π,才能激励所有的误差系数,因此给出如下转动方案:
1)以1°/s的角速度绕Z轴转动角度3π/4 rad;
2)以1°/s的角速度绕X轴转动角度3π/4 rad;
3)以1°/s的角速度绕Z轴转动角度5π/4 rad;
4)以1°/s的角速度绕X轴转动角度5π/4 rad.
3.1 系统模型1仿真结果
图1~图4所示为系统模型1在ps系下陀螺仪安装误差ΔT=[ΔT1ΔT2ΔT3]T、ΔM=[ΔM1ΔM2ΔM3]T和加速度计安装误差ηT=[ηT1ηT2ηT3]T、ΔηM=[ηM1ηM2ηM3]T的估计误差曲线。从图1~图4中可以看出,所有安装误差的估计误差都可以收敛到0附近,表明系统模型1在ps系下是可观测的。

图1 系统模型1在ps系下的ΔT估计误差

图2 系统模型1在ps系下的ΔM估计误差
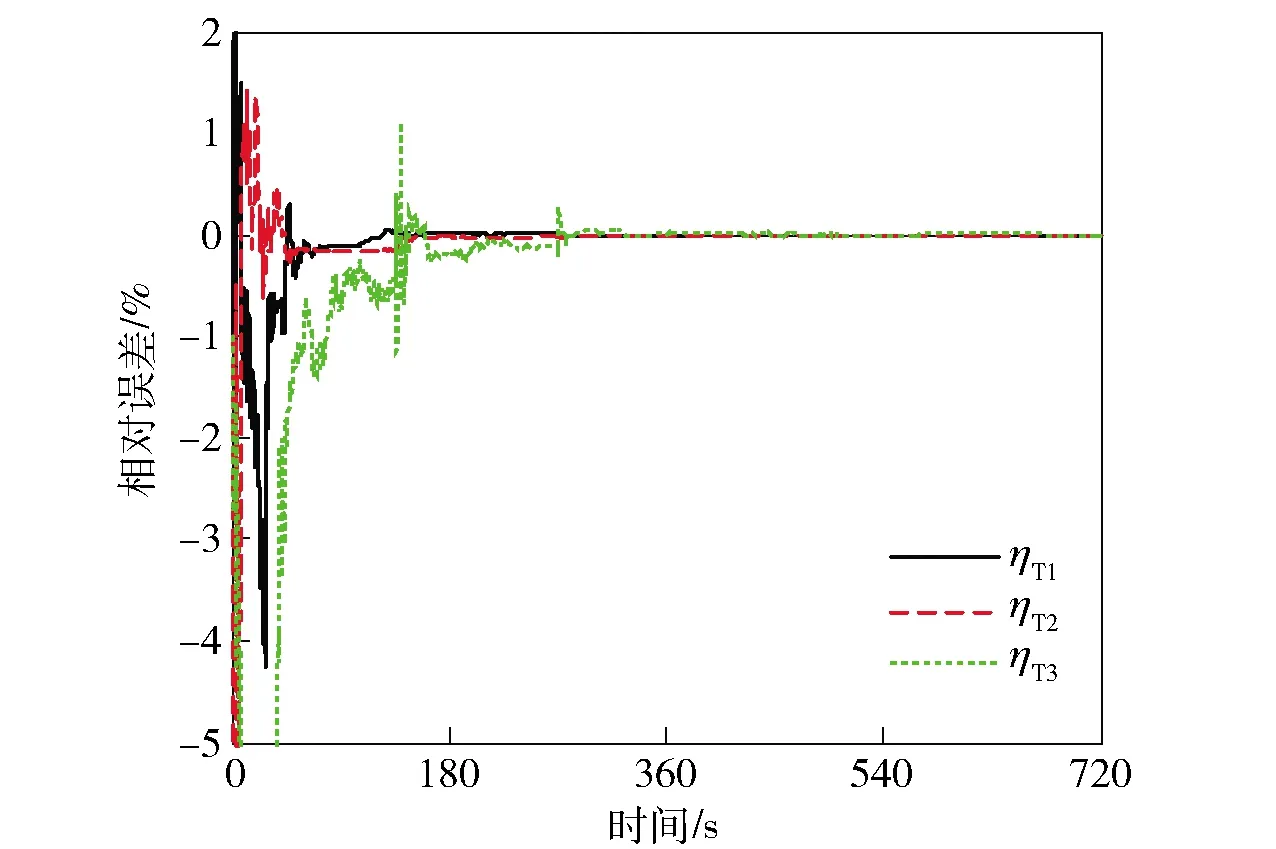
图3 系统模型1在ps系下的ηT估计误差

图4 系统模型1在ps系下的ηM估计误差
图5~图7所示为系统模型1在pa系下陀螺仪和加速度计安装误差的估计误差曲线。同样,所有安装误差的估计误差都可以收敛到0附近,表明系统模型1在pa系下是可观测的。
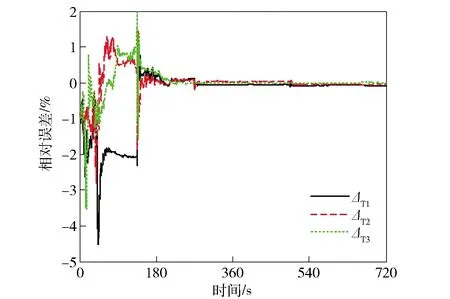
图5 系统模型1在pa系下的ΔT估计误差
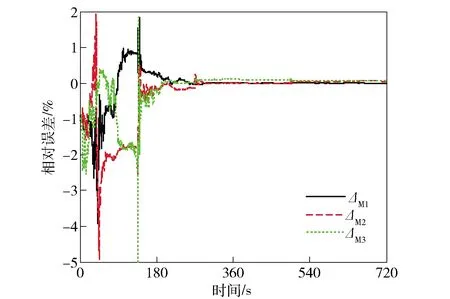
图6 系统模型1在pa系下的ΔM估计误差

图7 系统模型1在pa系下的ηT估计误差
3.2 系统模型2仿真结果
图8~图11给出了系统模型2中陀螺仪和加速度计安装误差的估计误差曲线。从图8~图11中可以看出,除了ΔT2,其余安装误差的估计误差均不能收敛到0,因此系统模型2是不完全可观测的。

图8 系统模型2中的ΔT估计误差

图9 系统模型2中的ΔM估计误差

图10 系统模型2中的ηT估计误差

图11 系统模型2中的ηM估计误差
3.3 系统模型3仿真结果
图12~图15所示为系统模型3中陀螺仪和加速度计安装误差的估计误差曲线。由图12~图15可以看出,加速度计安装误差的估计误差能够收敛到0附近,陀螺仪安装误差中,ΔT1和ΔM3并未受到激励,无法收敛;而其他安装误差的估计误差虽然收敛,但是估计误差较大。这是因为给出的转动方案只绕X轴和Z轴转动,导致作为陀螺仪安装误差激励的加矩角速度ωc的第2个分量为0,所以不能有效地激励所有的陀螺仪安装误差。

图12 系统模型3中的ΔT估计误差
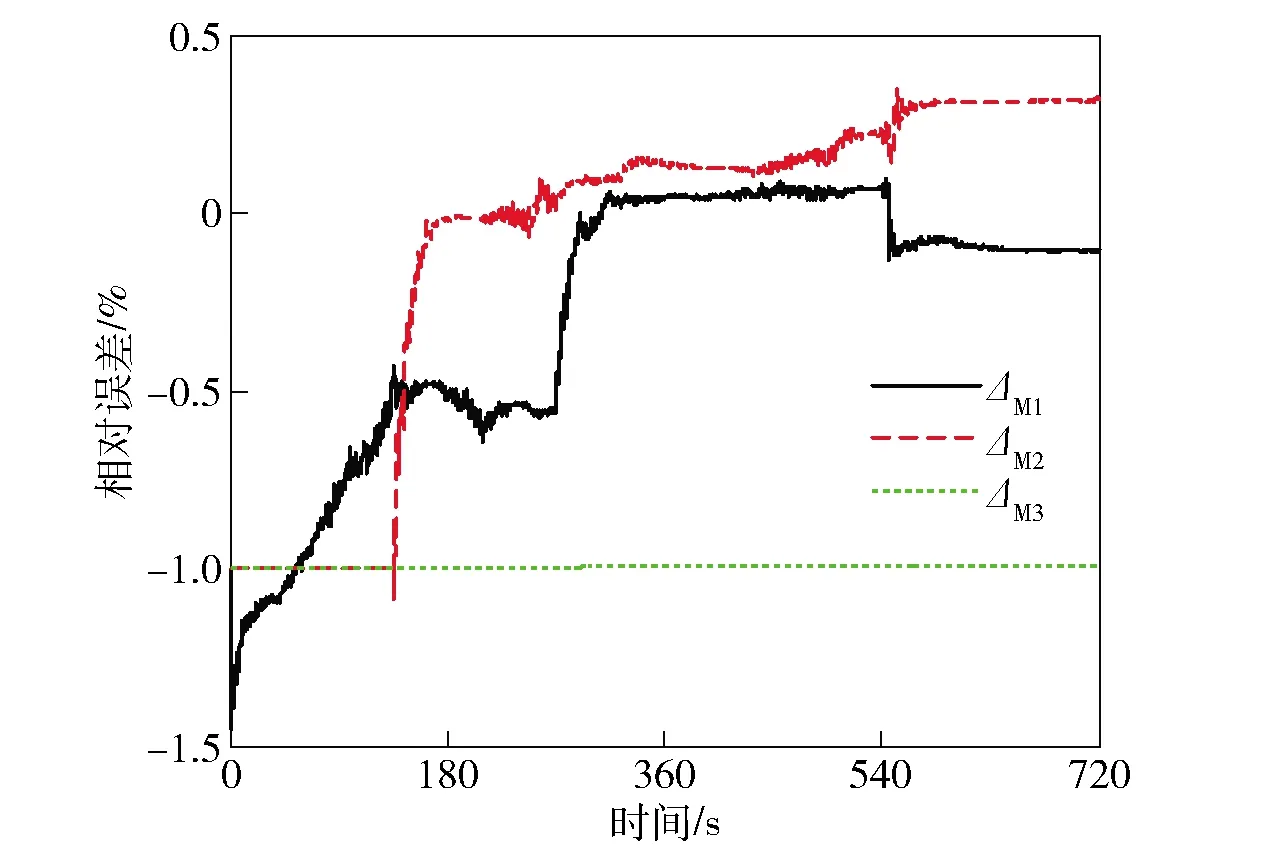
图13 系统模型3中的ΔM估计误差
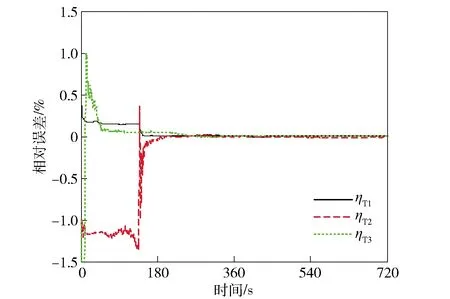
图14 系统模型3中的ηT估计误差

图15 系统模型3中的ηM估计误差
现在对原有的转动方案进行改动,增加绕Y轴的转动。
转动方案1:
1)以1°/s的角速度绕Z轴转动角度3π/4 rad;
2)以1°/s的角速度绕X轴转动角度3π/4 rad;
3)以1°/s的角速度绕Z轴转动角度5π/4 rad;
4)以1°/s的角速度绕X轴转动角度5π/4 rad;
5)以1°/s的角速度绕Y轴转动角度π rad.
图16~图19给出了系统模型3在转动方案1下陀螺仪和加速度计安装误差的估计误差曲线。由图16~图19可以看出,在增加绕Y轴转动后,加速度计安装误差的估计误差基本保持不变,而陀螺仪安装误差的估计误差都能够收敛到0附近。而且在图16和图17中明显可以看出,在原转动方案下未受到激励的ΔT1和ΔM3都是在绕Y轴转动时受到激励,误差曲线开始收敛,由此验证了2.3节中的结论。在选择框架角模型时,要求惯性导航系统的3个框架轴都可以全方位转动,使加矩角速度ωc的3个分量都不为0,才能激励所有的陀螺仪安装误差。
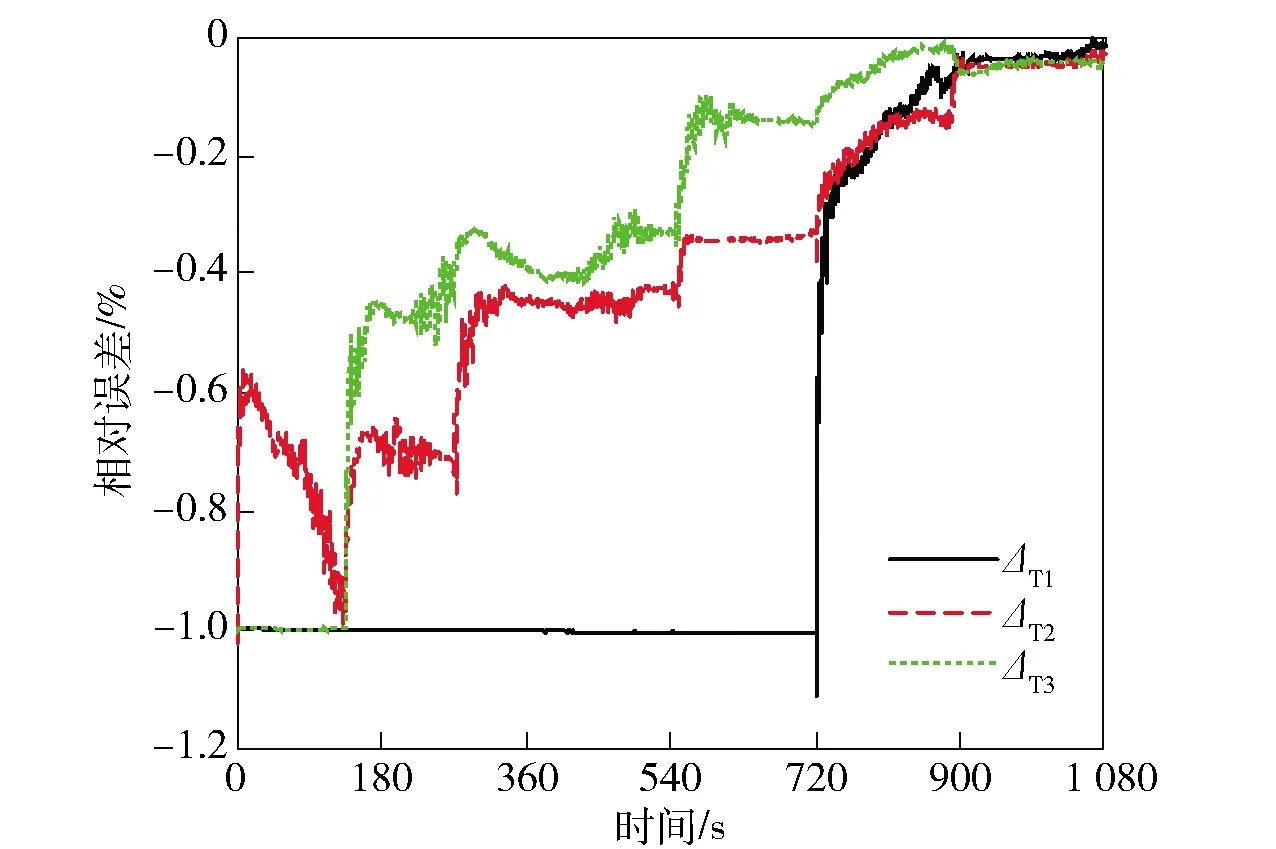
图16 系统模型3在转动方案1下的ΔT估计误差

图17 系统模型3在转动方案1下的ΔM估计误差

图18 系统模型3在转动方案1下的ηT估计误差

图19 系统模型3在转动方案1下的ηM估计误差
表1给出了经过多次仿真求均值的陀螺仪和加速度计安装误差的估计误差,结果与前面的分析基本一致。从表1中可以看出,在系统模型1和系统模型3的仿真结果中,加速度计安装误差的估计误差要小于陀螺仪安装误差,从而证明了前文得出的加速度计安装误差的可观测性优于陀螺仪安装误差的结论。同时可以看出,系统模型2中所有的安装误差系数都没有收敛到真值,这是因为从模型整体来看,系统模型2是不可观测的。在模型整体不可观测的情况下,无法对模型中的误差系数进行有效辨识,是因为对误差系数进行辨识的过程是对整个系统的所有状态量进行估计,不可观测的状态量会对卡尔曼滤波的时间更新和量测更新过程带来误差,因此可能导致可观测的状态量也无法收敛。
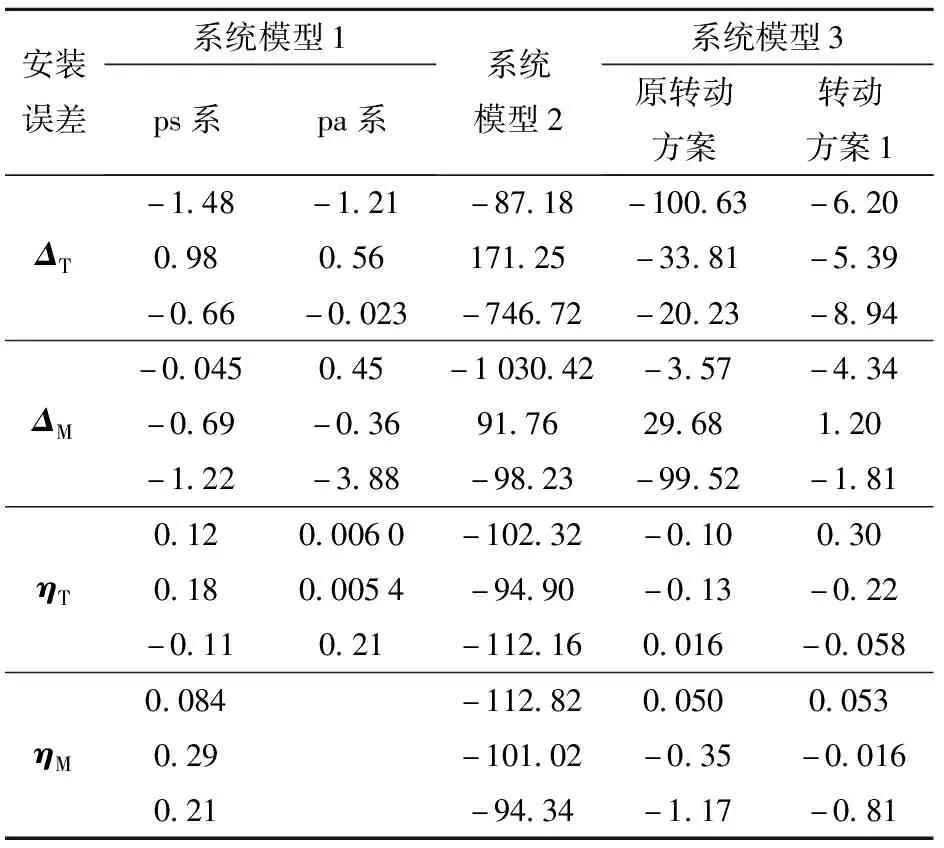
表1 3个系统模型下惯性仪表安装误差的估计误差
4 试验验证
由于实验室没有混合式惯性导航系统,本文使用某型平台式惯性导航系统进行了试验验证。由于硬件限制,只实现了转动方案1的前两步,即:
1)以1°/s的角速度绕Z轴转动角度3π/4 rad;
2)以1°/s的角速度绕X轴转动角度3π/4 rad.
在采集得到加速度计输出后,运用在pa系下的系统模型1和系统模型3进行了误差标定。下面给出两个模型下安装误差的估计曲线。
图20~图22为系统模型1在pa系下陀螺仪和加速度计安装误差的估计曲线。对比图5~图7的仿真结果可以看出,除了ηT1由于转动角度不足而未能收敛以外,其他安装误差都能够收敛,收敛速度也与仿真结果相符合。

图20 系统模型1在pa系下的ΔT估计曲线

图21 系统模型1在pa系下的ΔM估计曲线
图23~图26为系统模型3中陀螺仪和加速度计安装误差的估计曲线。从图23~图26中可以看出,与理论分析结果一致,由于惯性导航系统只绕X轴和Z轴转动,陀螺仪安装误差未受到充分激励,无法收敛。这与图12~图15的仿真结果也是一致的。

图25 系统模型3中的ηT估计曲线

图26 系统模型3中的ηM估计曲线
5 结论
本文针对混合式惯性导航系统连续自标定的系统模型选择问题,从模型中惯性仪表安装误差的可观测性分析出发,分析了不同系统模型的可观测性和适用条件。主要得出以下结论:
1)在选择失准角方程建立系统模型时,观测量应为加速度计输出,此时系统模型在ps系和pa系下都是可观测的,且在pa系下比在ps系下少3个加速度计安装误差。
2)在选择框架角方程建立系统模型时,必须以平台六面体为基准定义平台坐标系,即选择ps系。此时,为保证系统可观测,观测量应选择加速度计输出和平台框架角传感器输出,并且要求惯性导航系统绕3个框架轴都进行转动,使加矩角速度ωc的3个分量都有输入,以激励所有的陀螺仪安装误差。
3)在3种可观测的系统模型下,加速度计安装误差的可观测阶数都低于陀螺仪安装误差,证明加速度计安装误差的可观测性优于陀螺仪安装误差,具体表现在误差系数估计的精度更高,估计速度更快。
以上结论为混合式惯性导航系统连续自标定的系统模型建立提供了选择依据,并为下一步转动方案设计提供了一定理论基础。
