基于颗粒流的高填黄土减载明洞土拱效应分析

姚玉相，李盛，马莉，王焕，于本田，王长丹

基于颗粒流的高填黄土减载明洞土拱效应分析

姚玉相1，李盛1，马莉2，王焕3，于本田1，王长丹4

(1. 兰州交通大学 道桥工程灾害防治技术国家地方联合工程实验室，甘肃 兰州 730070；2. 兰州工业学院 土木工程学院，甘肃 兰州 730050；3. 中铁十四局集团有限公司，山东 济南 250014；4. 同济大学 道路与交通工程教育部重点实验室，上海 201804)

实际工程表明，在高填方明洞顶部铺设EPS板可以明显降低洞顶竖向土压力，然而，铺设EPS板会将明洞上方的土体荷载向其两侧土体转移，导致其侧墙所受水平土压力及弯矩增大。为了进一步减小明洞受力，提出一种新型减载明洞体系，利用颗粒流软件建立相应数值模型，从竖向、水平土压力、颗粒竖向位移、颗粒间接触力和孔隙率等细观层面研究该减载明洞的荷载传递机制。此外，基于该减载体系，分析EPS板距拱顶位置、宽度和填土压实度对明洞土拱效应的影响。研究结果表明：该减载体系可以扩大土拱效应的影响范围，同时减小洞顶与洞侧土压力；土拱效应的发展与洞顶土体孔隙率的变化相关，孔隙率随EPS板距拱顶距离的增加逐渐减小，土拱效应逐渐减弱，洞顶土压力逐渐增大；随EPS板宽度的增加先增大后减小，当EPS板宽度=1.5时，孔隙率达到最大值，土拱效应最强，洞顶荷载分布最少；填土压实度越大，柱土应力比越大，洞顶土压力越小。

新型减载明洞体系；颗粒流；土拱效应；微观

在西部铁路建设中，为缓解城市用地紧张，高填明洞在公路和铁路工程中的应用日益普遍，然而，明洞与土体刚度差异引起的洞顶土压力集中往往会造成洞顶纵向开裂，进而导致工程事故的发生。为保证明洞衬砌结构的安全性和稳定性，提高结构的耐久性，有必要对高填方黄土明洞的卸载体系的构成及荷载传递机理进行深入研究。国内外学者对填方结构物土压力减载进行了研究，并取得了一定的成果。Marston[1]最早提出并验证了高填方涵洞(管)结构的ITI卸载法，即在其顶部铺设可压缩柔性材料进行土压力减载。随后Dancygier等[2-6]通过室内或现场试验，在结构物顶部铺设柔性材料或EPS板，研究结构-土相互作用的影响，进一步得出在结构物顶部铺设柔性材料或EPS板可以起到很好的减载效果。Sun等[7]在涵顶铺设EPS板进行减载，运用FLAC4.0软件研究涵顶、涵底、涵测土压力变化规律。李盛等[8]通过室内模型试验研究EPS板对明洞的卸载效果及机制，得出EPS板密度越小，厚度越大，明洞洞顶垂直土压力的卸载越明显。姜峰林等[9-10]结合某一高填方涵洞实际工程对涵洞土压力及EPS板压缩变形进行了观测，探讨了不同EPS板厚度下涵顶土压力的减载特性，结果表明，EPS板可明显减小涵洞顶土压力。上述研究结果表明，采取减载措施能够有效减小涵洞或明洞结构物顶部的垂直土压力，然而，采取减载措施会将结构物上方的土体荷载转移到结构物两侧土体上，导致其侧墙所受水平土压力及弯矩增大[11]。为了进一步减小明洞受力，本文提出一种新型减载式明洞体系，即在明洞两侧边坡上设置混凝土柱，使混凝土柱与边坡成为整体结构，然后在洞顶铺设EPS板，形成EPS板+混凝土柱的减载式明洞。利用基于离散元理论的颗粒流软件PFC2D，从散粒体和微观角度分析该减载明洞土拱效应的变化规律及荷载传递机制。同时，基于该减载体系，进一步研究EPS板放置位置、EPS板宽度和填土压实度等3因素对土拱效应的影响。

1 基于颗粒流方法的分析

1.1 室内模型试验概述

根据模拟相似分析与加载条件，确定模型的几何相似比尺为1/25，最大模拟洞顶填土高度为25 m。按照该比例自制刚性圆拱形明洞模型，填土模型槽边坡坡角为70°，选用黄土进行分层填筑、压实。室内模型试验的模型尺寸、相关材料性质及参数等详细信息见文献[12]。

1.2 颗粒流数值模型建立

目前，利用PFC2D颗粒流软件生成土的初始模型的方法有半径扩张重力沉降法[13]、UCM法[14]和IMCM法[15]。利用前2种方法生成的初始模型可能会存在过大的水平应力，并且地应力也不是沿深度的梯度场，与实际情况不符。为获得更高精度的初始应力状态模型，减小生成初始模型时的水平应力，本文采用前述第3种方法，即改进的多层压实方法(IMCM)生成初始模型。为了进行对比，分别建立无减载、EPS板减载和EPS板+混凝土柱减载3种数值模型。

由于上述各数值模型建立过程相似，此处仅对EPS板+混凝土柱减载的建模过程进行详细介绍，相应数值模型图如图1所示。模型中所有边界条件(边坡、明洞、地基和混凝土柱)均采用边界墙(wall)模拟，填土采用圆盘颗粒模拟，并利用IMCM法将填土分层填筑在边坡坡脚为70°的梯形模型箱内。模型箱的高度为1.3 m，其中，明洞高度为0.2 m，EPS板的厚度为0.15 m，回填土高度为0.85 m，空白区域的高度为0.1 m；模型箱底部的长度为0.6 m，其中，明洞宽为0.2 m；混凝土柱位于明洞两侧边坡处，其高度为坡底至EPS板顶的距离，详细位置见图2所示。生成EPS板时，先在放置EPS板的位置处生成一个矩形墙(长0.2 m×高0.15 m)，并删除该矩形墙内的颗粒，然后利用PFC2D自带的半径扩大法程序[16]生成颗粒集合。此时，由于矩形墙的介入，模型整体处于不平衡状态，故需要将模型运行足够多的步数来获得初始平衡状态，模型达到初始平衡状态以后，删除矩形墙，赋予模型合适的细观参数，并在重力的作用下达到最终平衡状 态[15, 17]。另外，模型中布置了一定数量的测量圆和位移测量点，用于测量模拟中各位置的竖向、水平土压力、孔隙率和颗粒竖向位移。其中，编号1~11的测量圆用于测量洞顶竖向应力，编号4~8的测量圆用于计算洞顶平均竖向应力，编号5~7的测量圆用于测量洞顶上方土体中的孔隙率，编号12~15的测量圆用于测量混凝土上的竖向应力，编号16~20的测量圆用于测量混凝土柱之间土体的竖向应力，编号6和21~29的测量圆用于测量拱顶上方不同深度位置处的竖向应力，明洞两侧重叠的测量圆用于测量明洞两侧土体的水平应力，具体位置见图 2。

单位：m

1.3 材料细观参数获取

填土材料选用相对压实度=80%，孔隙率= 0.2，黏聚力c=20 kPa，=24.6°的黄土[18]，由于黄土是一种黏性材料，故填土材料颗粒间的接触模型采用线性接触黏结本构模型，颗粒粒径分布范围为6~10 mm。通过建立数值双轴试验模型进行反演试算获得其细观参数，最终使颗粒集合表现的宏观特性与预设的宏观特性一致，数值模型采用的细观参数见表1。双轴试验试样尺寸为宽0.5 m×高1.0 m，采用PFC自带的伺服机制进行加载，伺服围压分别为50，75和100 kPa，加载应力应变曲线如图3所示(压实度=85%，孔隙率=0.15，黏聚力=31.1 kPa，=28.2°；压实度=90%，孔隙率=0.1，黏聚力=58.1 kPa，=30.2°，图类同)。

图2 测点位置示意图

模拟EPS板时，颗粒间的接触本构选择线性接触本构，颗粒粒径服从标准正态曲线分布，其细观参数通过数值压缩试验进行反演试算获得，试样尺寸为宽0.4 m×高0.8 m。通过给上压板施加10-8m/step的恒定向下速度进行加载，并记录相应的应力和应变数据。经过大量的试算，最终确定其合理的应力应变曲线，如图4所示，相应的细观参数见表1。由图4可知：当EPS板的应变在4%以内变化时，DEM曲线和室内试验曲线吻合较好。事实上，在进行本次数值模拟时，EPS板的应变远小于4%。因此，在本研究中可以采用表1中所列的EPS板细观力学参数来表征其力学行为[8]。

图3 双轴试验模拟结果

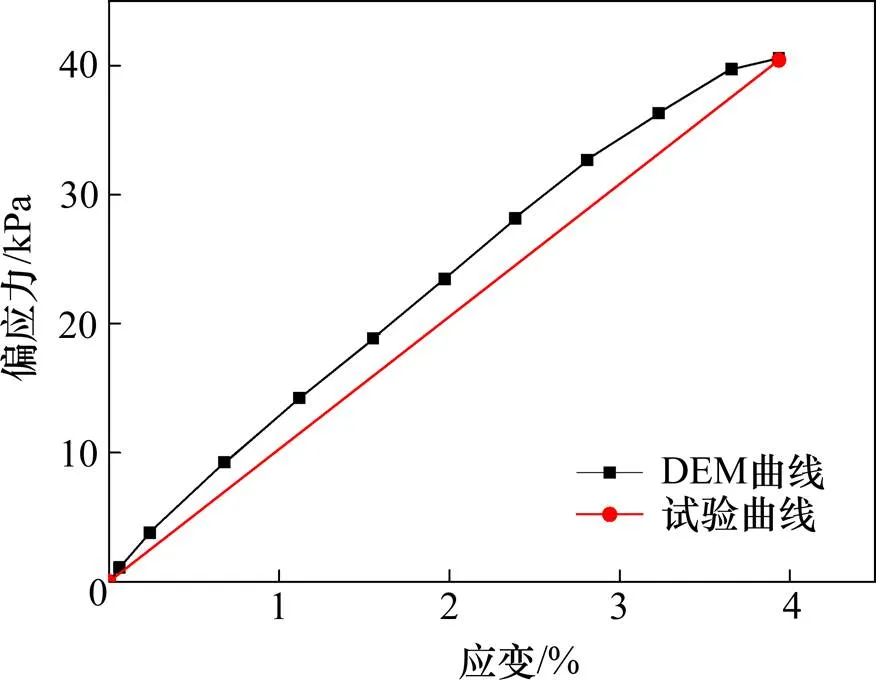
图4 EPS板压缩模拟和试验曲线比较

表1 颗粒流模型细观参数

2 计算结果与分析

2.1 颗粒间接触力分析

图5为无减载、EPS板减载和EPS板+混凝土柱减载3种情况下颗粒间的接触力分布。接触力的分布实质是土体中荷载传递特征的体现，图中Compression和Tension分别表示压力和拉力，出现拉力是因为填土本身就具有黏性，颗粒间存在黏聚力。线的粗细代表接触力的大小，线条组成的网络结构形式代表力的分布和荷载的传递方向。图5(a)显示：无减载措施条件下，洞顶接触力集中现象明显，洞顶土颗粒间接触力明显大于明洞两侧土颗粒间接触力。在只有EPS板减载的情况下，如图5(b)所示。洞顶上方土体荷载传递至EPS板顶时，由于EPS板与周围填土材料的刚度差异性，洞顶荷载向EPS板两侧转移并向下发展；当荷载转移至与EPS板底面平行位置处时，一部分荷载继续向下发展至坡底，另一部分荷载拐向拱形明洞的拱脚附近。这是因为：1) 明洞拱脚处的刚度与其周围填土刚度存在差别，在土拱效应的作用下，荷载向拱脚转移；2) 明洞的拱形部分与明洞侧墙接合处有一定的尖角，该尖角附近会产生应力集中。当在明洞两侧边坡处设置混凝土柱时，如图5(c)所示。颗粒间接触力链的分布发生了明显的变化，明洞侧墙受力明显减小，土拱效应影响的范围进一步扩大(见图5(c)中弧形虚线所示)。这是因为：1) 混凝土柱有效的限制了明洞两侧土体下沉，使明洞上方较大范围内(混凝土柱之间)的土体产生不均匀沉降，从而扩大了土拱效应影响的范围；2) 由于混凝土柱与明洞两侧填土之间的刚度差异，EPS板卸载的洞顶荷载并未向明洞两侧土体发展，而是转移至混凝土柱上，使明洞侧墙受力显著减小。

(a) 无减载；(b) EPS板减载；(c) EPS板+混凝土柱减载

2.2 应力分析

根据图2中布置的测量圆，并使用程序自带的测量圆命令，对明洞上方的竖向土压力、不同深度位置处的竖向土压力和明洞两侧的水平土压力进行监测和记录，相应计算结果如图6~8所示。图6为不同减载措施下竖向土压力沿深度方向(图2中测量圆6和21~29位置处)变化规律。图6显示，明洞顶无减载措施时，竖向土压力随深度的增加逐渐增加，增幅逐渐变大；洞顶采取减载措施后，竖向土压力随深度的增加先增加后减小，说明土拱效应出现，洞顶上方荷载转移至其他位置；减载措施不同，土拱效应出现的位置也不一样，对于EPS板减载而言，竖向土压力在距明洞顶上方40 cm的位置处开始减小，此高度即为土拱高度，且为明洞高度的2倍；对于EPS板+混凝土柱减载而言，距明洞顶上方50 cm位置处竖向土压力开始减小，此时土拱高度为明洞高度的2.5倍。由图7可知，对于无减载措施情况而言，由于明洞和两侧填土的刚度差异，导致明洞两侧外土柱沉降大于内土柱沉降，外土柱对内土柱产生了向下的摩擦力，从而使明洞上方的竖向压力大于其两侧的竖向土压力。在明洞顶铺设EPS板后，由于EPS板受到上覆土体向下的压力，发生向下的变形，导致内土柱沉降大于外土柱沉降，土拱效应出现，洞顶荷载向明洞两侧转移。相比无减载措施情况下的竖向土压力，此时，明洞洞顶受力明显减小，而洞侧受力增大，且明洞顶部中心土压力的卸载率为80%。在明洞两侧设置混凝土柱后，相比无减载措施情况，由于洞顶上方土体荷载向混凝土柱转移，明洞洞顶和洞侧的竖向土压力都显著减小，且明洞顶部中心土压力的卸载率为87%。由图8可知，明洞两侧的水平土压力随深度的增加逐渐增大，但增幅不大，整体分布较均匀，洞顶无减载时，洞侧所受平均水平土压力13.7 kPa；相比无减载措施情况，EPS板减载时，由于内外土柱的不均匀沉降，洞顶荷载向明洞两侧转移，洞侧水平土压力增加，洞侧所受平均水平土压力18.8 kPa；EPS板+混凝土柱减载时，由于混凝土柱的存在，洞顶荷载及明洞两侧荷载向混凝土柱转移，洞侧水平土压力减小，相应的平均水平土压力为10.6 kPa。综上，混凝土柱的存在既保证了洞顶安全受力又保证了明洞侧墙结构的安全性和稳定性。

图6 不同减载措施下竖向应力沿深度方向变化规律

图7 不同减载措施下明洞顶竖向土压力变化规律

图8 不同减载措施下明洞顶水平土压力变化规律

2.3 竖向位移分析

图9为不同减载措施情况下颗粒的竖向位移变化。图9显示：无减载措施情况下颗粒位移呈现出中间小，两头大的特点，即内土柱沉降小于外土柱沉降，内外沉降差为0.07 mm，此时，外土柱对内土柱会产生向下的摩擦力，洞顶土压力增大。当在洞顶上方铺设EPS板后，由于EPS板具有较大的压缩变形空间，洞顶上方内土柱沉降明显大于其两侧土柱的沉降，沉降差为-0.17 mm；EPS板+混凝土柱减载时，明洞两侧混凝土柱能够有效阻止外土柱的沉降，进一步增大内土柱的沉降，沉降差为-0.33 mm；这2种情况下，外土柱均会对内土柱产生向上的摩擦力，洞顶土压力减小，且负的沉降差越大，土拱效应越明显，洞顶荷载转移越多。

图9 不同减载措施下明洞顶颗粒竖向位移变化规律

3 参数分析

为明确EPS板放置位置、宽度和填土压实度对高填黄土明洞土拱效应的影响规律，以EPS板+混凝土柱减载情况作为参数化研究的基准，分析EPS板位置、宽度和填土压实度对洞顶土拱效应的影响。其中，EPS板底面距拱顶的距离为0，2和5 cm；EPS板的宽度分别为10(0.5)，20(1.0)，30(1.5)和40 cm(2.0)；填土压实度分别为：80%，85%，90%。

3.1 EPS板位置的影响

图10为EPS板不同位置情况下洞顶平均竖向土压力和颗粒竖向相对位移分布曲线。由图10可知：洞顶平均土压力随EPS板距拱顶距离的增大而增大，颗粒竖向相对位移随EPS板距拱顶距离的增大而减小。这说明，EPS板距离拱顶越近，内外土柱沉降差越大，土拱效应越强，洞顶土压力越小。孔隙率随EPS板距拱顶位置的变化见图11。由图11可知，随着EPS板距拱顶距离的减小，洞顶上方土体孔隙率逐渐增大。这是由于土拱效应的发展对应于土体中孔隙率的变化过程，当土拱效应逐渐增强时，洞顶上方的填土荷载逐渐转移至混凝土柱，洞顶上方的土体荷载减小，故孔隙率变大。综上，建议在实际工程中铺设EPS板时，尽可能靠近 拱顶。

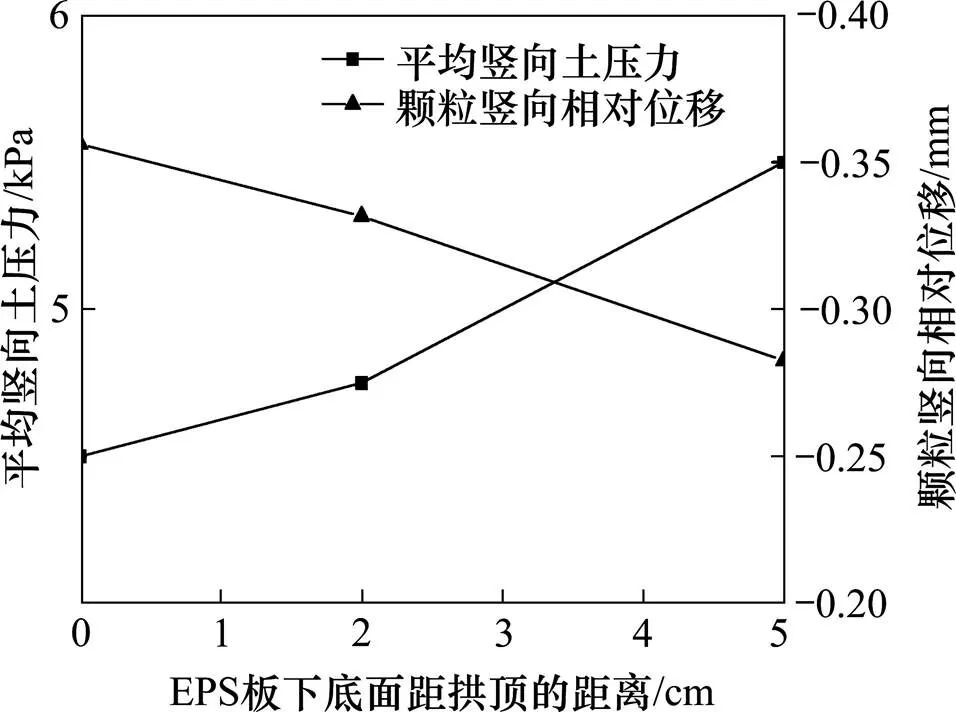
图10 明洞洞顶平均竖向土压力和颗粒竖向相对位移与EPS板位置关系

3.2 EPS板宽度的影响

明洞洞顶平均竖向土压力和颗粒竖向相对位移随EPS板宽度的变化见图12。由图12可知，随着EPS板宽度的增大，平均竖向土压力先减小，并在EPS板宽度=1.5时达到最小值3.5 kPa，之后又开始增大；而颗粒竖向相对位移则是先增大，并在EPS板宽度=1.5时达到最大值0.41 mm，而后开始减小。这说明，相同填土高度下，EPS板宽度对土拱效应的影响存在上限值，且该上限值为=1.5。

图12 明洞洞顶平均竖向土压力和颗粒竖向相对位移与EPS板厚度关系

孔隙率随EPS板宽度的变化见图13。由图13可知，洞顶上方土体孔隙率随EPS板宽度的增加先逐渐增大，并在EPS板宽度=1.5时达到最大值0.149，随后开始减小。结合图12与图13的相关分析可知，EPS板最佳宽度为=1.5。此时，洞顶内外土柱沉降差达到最大，土拱效应最强，洞顶荷载分布最少，土体孔隙率最大，且该值与Vaslestad等[3, 19]推荐的值相一致。

图13 孔隙率与EPS板宽度关系

图14 明洞洞顶平均竖向土压力和柱土应力比与填土压实度关系

3.3 填土压实度的影响

压实度不同，填土材料所表现的性质也不一样，压实度越大，填土材料的孔隙率越小，内摩擦角和黏聚力越大。图14为不同压实度情况下明洞洞顶平均竖向土压力和柱土应力比(混凝土柱上的平均应力与混凝土柱间土体平均应力之比)变化曲线。由图14可知，随填土压实度的增加，柱土应力比逐渐增大，洞顶平均土压力逐渐减小。上述结果表明，填土压实度越大，明洞顶土拱效应越明显，填土颗粒间形成土拱结构稳定性越强，混凝土柱承担的荷载越多，洞顶荷载分布越少。理由如下：填土压实度越大，颗粒间内摩擦角越大，颗粒间咬合嵌锁作用越强，越容易形成稳定的土拱结构。

4 结论

1) 明洞两侧边坡处设置混凝土柱不仅能够有效降低洞顶两侧土体的沉降，间接增加内土柱的沉降，加强土拱效应，还能同时减小洞顶垂直土压力和明洞侧墙所受土压力。与EPS板减载的明洞相比，EPS板+混凝土柱减载明洞的减载效果提高了7%，侧墙受到的水平土压力减少了44%。

2) 土体孔隙率的变化与土拱效应的发展相关，改变EPS板距拱顶的距离和宽度均会引起明洞上方土体孔隙率的变化，进而影响土拱效应。孔隙率随EPS板距拱顶距离的增加呈线性减小，土拱效应逐渐减弱，洞顶土压力逐渐增大；孔隙率随EPS板宽度的增加呈非线性变化，当EPS板宽度=1.5时，洞顶上方土体孔隙率达到最大，土拱效应达到最强，洞顶减载效果最优。

3) 填土压实度越大，土体内摩擦角越大，颗粒间咬合嵌锁作用越强，明洞上方形成的土拱结构越稳定，土拱效应发挥的作用越持久，洞顶上方荷载持续向其他方向转移，洞顶土压力越小。

[1] Marston A. The theory of external loads on closed conduits in the light of the latest experiments[C]// Proceedings of Highway Research Board. Washington D.C.:[s.n.], 1930: 138-170.

[2] Dancygier A N, Yankelevsky D Z. A soft layer to control soil arching above a buried structure[J]. Engineering Structures, 1996, 18(5): 378-386.

[3] Vaslestad J, Johansen T H, Holm W. Load reduction on rigid culverts beneath high fills: Long-term behavior[J]. Transportation Research Record,1993, 1415: 58-68.

[4] Okabayashik, Ohtaniw, Akiyamak, et al. Centrifugal model test for reducing earth pressure on the culvert by using the material[C]// Poceedings of the Polar Engineering Conference. Osaka: International Society of Offshore and Polar Engineers, 1994: 620-624.

[5] 白冰. 高填土下刚性结构物竖向土压力减荷方法[J]. 岩土力学, 1997, 18(1): 35-39. BAI Bing. The measure for reducing the vertical earth pressure on the buried rigid structure[J]. Rock and Soil Mechanics, 1997, 18(1): 35-39.

[6] 顾安全. 上埋式管道及洞室垂直土压力的研究[J]. 岩土工程学报, 1981, 3(1): 3-15. GU Anquan. Investigation of the vertical earth pressure on projecting conduit and underground chamber under a high embankment[J]. Chinese Journal of Geotechnical Engineering, 1981, 3(1): 3-15.

[7] Sun L C, Hopkins T, Beckham T. Stress reduction by ultra-lightweight geofoam for high fill culvert: numerical analysis[C]// 13th Great Lakes Geotechnical and Geoenvironmental Conference, 2005, Milwaukee, Wisconsin, USA. Reston, VA, USA: American Society of Civil Engineers, 2005.

[8] 李盛, 李善珍, 王起才, 等. EPS板卸载的高填黄土明洞模型试验和数值模拟分析[J]. 岩石力学与工程学报, 2016, 35(增1): 3394-3401. LI Sheng, LI Shanzhen, WANG Qicai, et al. Unloading model test and numerical simulation analysis on high fill loess open cut tunnel with EPS[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Suppl 1): 3394-3401.

[9] 姜峰林. 高填方涵洞EPS板减荷技术应用及数值模拟研究[D]. 西安: 长安大学, 2010. JIANG Fenglin. EPS load reduction technology application and numerical simulation for high fill culert[D]. Xi’an: Chang’an University, 2010.

[10] 张卫兵, 刘保健, 谢永利. 基于EPS减荷措施的高填涵洞试验研究[J]. 公路交通科技, 2006, 23(12): 54-57, 98. ZHANG Weibing, LIU Baojian, XIE Yongli. Field test and numerical simulation study on the load-reducing effect of EPS on the highly filled culvert[J]. Journal of Highway and Transportation Research and Development, 2006, 23(12): 54-57, 98.

[11] 陈保国, 宋丁豹, 焦俊杰, 等. 减载条件下高填方涵洞垂直土压力研究[J]. 华中科技大学学报(自然科学版), 2015, 43(10): 112-116. CHEN Baoguo, SONG Dingbao, JIAO Junjie, et al. Vertical earth pressure on high fill culverts under load reduction condition[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015, 43(10): 112-116.

[12] 李盛, 马莉, 王起才, 等. 高填黄土明洞卸载结构土压力模型试验和数值模拟分析[J]. 岩土工程学报, 2016, 38(4): 636-642. LI Sheng, MA Li, WANG Qicai, et al. Model tests and numerical simulations of earth pressure for unloading structures of high fill open cut tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 636-642.

[13] Bhandari A, HAN Jie. Investigation of geotextile-soil interaction under a cyclic vertical load using the discrete element method[J]. Geotextiles and Geomembranes, 2010, 28(1): 33-43.

[14] Jiang M J, Konrad J M, Leroueil S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597.

[15] LAI Hanjiang, ZHENG Junjie, ZHANG Jun, et al. DEM analysis of “soil”-arching within geogrid-reinforced and unreinforced pile-supported embankments[J]. Computers and Geotechnics, 2014, 61: 13-23.

[16] Itasca Consulting Group, Inc. PFC2D: Particle flow code in 2 dimensions (Version 3.1)[R]. Minneapolis: Itasca Consulting Group, Inc., 2004.

[17] HAN Jie, Bhandari A, WANG Fei. DEM analysis of stresses and deformations of geogrid-reinforced embankments over piles[J]. International Journal of Geomechanics, 2012, 12(4): 340-350.

[18] LI S. Study on vertical earth pressure characteristic and calculation method of unloading structure for high fill loess open cut tunnel[J]. Soil Mechanics and Foundation Engineering, 2019, 56(3): 184-190.

[19] Kim K, Yoo C H. Design loading on deeply buried box culverts[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(1): 20-27.

Analysis on soil arching for unloading structure of high-filled cut-and-cover tunnel based on particle flow simulation

YAO Yuxiang1, LI Sheng1, MA Li2, WANG Huan3, YU Bentian1, WANG Changdan4

(1. National and Provincial Joint Engineering Laboratory of Road & Bridge Disaster Prevention and Control, Lanzhou Jiaotong University,Lanzhou 730070, China; 2. College of Civil Engineering, Lanzhou Institute of Technology, Lanzhou 730050, China;3. China Railway Fourteen Bureau Group Co., Ltd, Jinan 250014, China;4. Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China)

The practical engineering shows that laying EPS board on the top of high-filled cut-and-cover tunnel can obviously reduce the vertical earth pressure. However, it will transfer the soil load on the top of high-filled cut-and-cover tunnel to its two sides, resulting in the increase of horizontal earth pressure and bending moment. In order to further reduce the stress around the cut-and-cover tunnel, a new type of unloading structure system was proposed in this paper, and the software Meso-scale Particle Flow Code was used to establish the corresponding numerical model. The influence laws of soil arching for unloading structure system were studied from the mesoscopic level of vertical soil pressure, vertical displacement of particles and contact force chain between particles. In addition, based on this system, the influence of location and the width of EPS, the compaction degree of the filled soil on the soil arching was analyzed. It is shown that this system can expand the influence range of soil arching and reduce the earth pressure at the top and side of the cut-and-cover tunnel. The development of soil arching is related to the change of the porosity of soil on the roof. The porosity decreases with the increase of the distance between EPS plate and the top of cut-and-cover tunnel, the soil arching weakens and the soil pressure on the roof increases. As the width of EPS board increases, it first increases and then decreases. When the width of EPS board=1.5, the porosity reaches the maximum. The soil arching is the strongest, and the load on the top of cut-and-cover tunnel distribution is the least. The greater the compactness of the filling soil is, the greater the pillar-soil stress ratio is, and the smaller the earth pressure of the roof is.

new type of unloading structure system; PFC; soil arching; microcosmic viewpoint

10.19713/j.cnki.43-1423/u.T20190210

TU43

A

1672 - 7029(2020)01 - 0139 - 09

2019-03-25

国家自然科学基金资助项目(51668036，51868041)；长江学者和创新团队发展计划项目(IRT_15R29)；甘肃省高等学校科学研究一般项目(2017A-111)；甘肃省高校协同创新科技团队支持计划项目(2017C-08)；兰州交通大学优秀科研团队项目(201606)

李盛(1982-)，男，山西阳高人，副教授，博士，从事桥梁与隧道工程方向研究；E-mail：ligwin@126.com

(编辑 阳丽霞)