Blazar多波段有效谱指数关系研究∗
2020-02-12聂建军樊军辉庹满先汪胜辉曲孝海张月莲杨江河
聂建军 陈 怡 樊军辉 庹满先 汪胜辉 曲孝海 张月莲 杨江河
(1 湖南文理学院数理学院常德415000)
(2 广州大学天体物理中心广州510006)
1 引言
耀变体(blazar)是活动星系核(Active galactic nucleus, AGN)中活动最剧烈的一类天体.根据发射线的不同,blazar可分为蝎虎天体(BL Lac object)和平谱射电类星体(Flat Spectral Radio Quasar, FSRQ).FSRQ有强发射线, 而BL Lac没有或仅有非常弱的发射线.根据blazar能谱分布(Spectral Energy Distribution, SED)同步峰频高低, blazar分为低同步峰频、中同步峰频和高同步峰频blazar, 分别记为LSP、ISP和HSP, 对于BL Lac天体分别记为LBL、IBL和HBL.在不同的文献中, 用于分类的同步峰频值存在差别[1–5].
多波段有效谱指数的关系可以帮助我们了解不同波段之间辐射机制的差异, 这可能会对AGN的辐射模型给出约束条件.不少作者研究了宽波段谱指数, 并给出一些宽波段谱指数之间的相关关系[1–3,6–11].
为了进一步研究有效谱指数的性质及多波段有效谱指数之间的关联, 本文收集了一个含有885个Fermi blazar大样本的射电、光学、X-ray及γ-ray辐射数据, 计算了它们的辐射流量密度和两两波段之间的6个有效谱指数; 分类研究了6个有效谱指数两两之间的相关性.本文中, 我们采用fν∝ ν−α定义谱指数, 式中fν为频率ν处的流量密度, α为谱指数; 我们采用文献[2]的方法对blazar进行分类.
2 样本及数据处理方法
由于Fermi-LAT (Large Area Telescope) 4期源表(4FGL)最近才发布, 其中新增的blazar还没有明确的分类,因此,本文以Fermi-LAT 3期源表(3FGL)[12–13]给出的blazar为样本, 在NED (NASA/ IPAC Extragalactic Database1http: //ned.ipac.caltech.edu/)及相关文献中查找射电、光学和X-ray辐射数据, γ-ray数据由Fermi-LAT给出.若一个源在某波段有多个观测数据, 数据选择原则是: 误差较小, 且靠近平均值.
首先, 从文献收集或者基于文献计算射电1.4 GHz、光学R波段(4.68 × 1014Hz)、X-ray 1 keV和γ-ray 1 GeV处的辐射流量密度; 然后用有效谱指数计算公式计算4个波段两两之间的6个有效谱指数, 即, 射电(R)到光学(O) (αRO)、射电(R)到X-ray (X)(αRX)、射电(R)到γ-ray (γ) (αRγ)、光学(O)到X-ray (αOX)、光学(O)到γ-ray (αOγ)、X-ray到γ-ray (αXγ).
通过转换3FGL中给出的blazar在1–100 GeV内的积分光子流量得到γ-ray 1 GeV处的流量密度, 计算方法详见文献[14–16].计算光学流量时, 先用NED中给出的消光数据对其进行银河系消光校正.对于所有的观测流量密度, 均由公式进行K改正, 式中: αν为频率ν处的谱指数, z为红移,为流量密度的观测值.在本文的计算中, 若红移和谱指数未知, 则用同类型样本的平均值代替.
有效谱指数计算公式[17]为αij= −lg(fi/fj)/lg(νi/νj), 式中, i、j分别对应不同波段, fi和fj分别为相应频率νi和νj处的流量密度.利用射电、光学、X-ray和γ-ray流量密度及有效谱指数计算公式, 可得到αRO, αRX, αRγ, αOX, αOγ和αXγ6个有效谱指数.
最后所得样本源及有效谱指数计算结果如表1所示.表1各列说明如下: 第1列是源的3FGL名称; 第2列为源的分类, 其中, F表示FSRQ, H表示HBL, I表示IBL, L表示LBL,该分类来自文献[2]; 第3列是源的红移; 第4–9列, 分别为计算得到的有效谱指数及其误差, 误差由谱指数计算公式根据误差传递规律计算得到.
由表1可知: 样本中共有885个blazar (至少有2个不同的有效谱指数), 其中, 386个FSRQ,499个BL Lac(242 HBL,130 IBL和127 LBL).885个blazar中,719个有αRO,594个有αRX, 843个有αRγ, 512个有αOX, 761个有αOγ, 636个有αXγ.BL Lac的分类来自文献[2].
3 结果
根据前面计算的有效谱指数(表1), 做αRO, αRX, αRγ, αOX, αOγ及αXγ任意2个有效谱指数之间的相关, 结果如图1所示.图1中, 红色空心圆圈代表FSRQ, 蓝色实心圆点代表HBL, 绿色三角形为LBL.对所有关系做线性回归分析, 得到blazar总样本以及其子类FSRQ和BL Lac (HBL和LBL)样本的任意2个有效谱指数的线性相关结果如表2所示.表2中: 线性回归方程可表示为y = (a±∆a)+(b±∆b)x, r为相关系数, p为机会概率, n为样本量; 第8列中“RC”表示两个有效谱指数的真实存在的相关性, 即拟合结果, “P”表示正相关, “A”表示反相关, “N”表示无相关; 第9列中“ST”表示4个波段能谱分布图中各波段连线关系的结构类型.I–VI表示6种结构类型, 其意义详见4.2节; 第10列中“SC”为结构类型所指示的两个有效谱指数之间的相关性.由于IBL是LBL到HBL的一类中间天体, 性质介于2者之间, 具有与BL Lac总样本类似的统计特征, 在分类统计时,其特征性质不明显, 因此, 本文未考虑IBL.
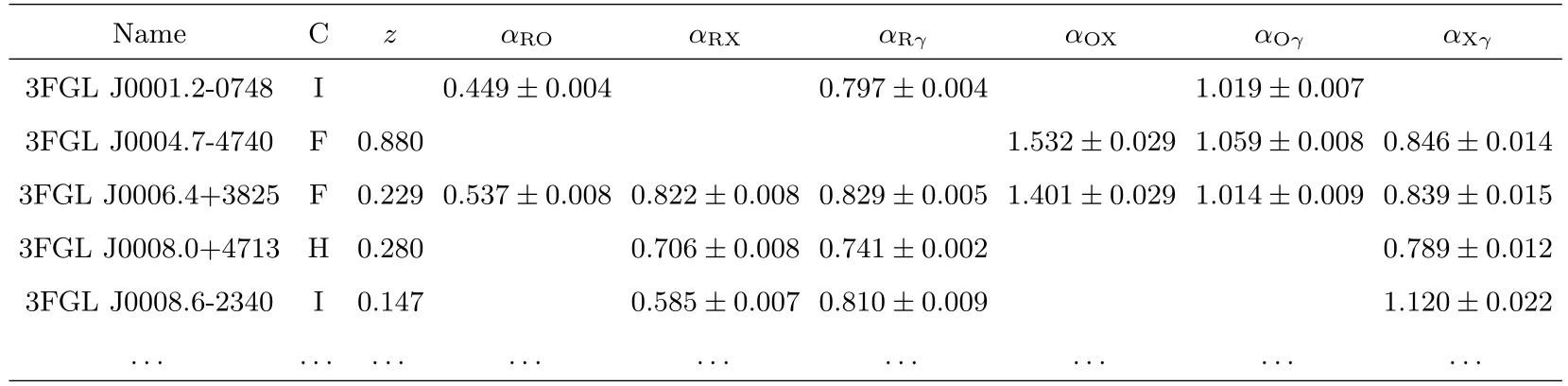
表1 样本及有效谱指数计算结果(完整表格见表3附录)Table 1 Blazars sample and the calculation results of effective spectral indices (See Appendix for complete samples)
4 讨论
4.1 函数拟合获得的相关性
根据表2, 对αRO, αRX, αRγ, αOX, αOγ及αXγ的任意2个有效谱指数之间的相关性概述如下.在下面的概述中, 字母T、F、B、H和L分别代表总样本、FSRQ、BL Lac、HBL和LBL样本.
(1)对于T、F、B、H、L样本, αRO−αRγ、αRX−αRγ、αOX−αOγ、αRX− αOX、αRγ− αOγ及αOγ− αXγ均有正相关;
(2)对于T、F、B、H、L样本, αRO− αOγ、αRX− αXγ及αOX− αXγ均有反相关或反相关趋势;
(3)对于T、F、B、L样本, αRO− αRX有正相关; 对于H样本, αRO− αRX无明显的正相关, 相关系数和机会概率分别为r =0.09, p=29.75%;
(4)对于F、H、L样本, αRγ− αXγ有正相关, 对T和B样本, αRγ− αXγ无明显的正相关, 相关系数和机会概率分别为r =0.04、p=33.82%和r =0.01、p=79.40%;
(5)对于T、F、H、L样本, αRO− αOX有反相关或反相关趋势, 对于B样本, αRO−αOX无相关;
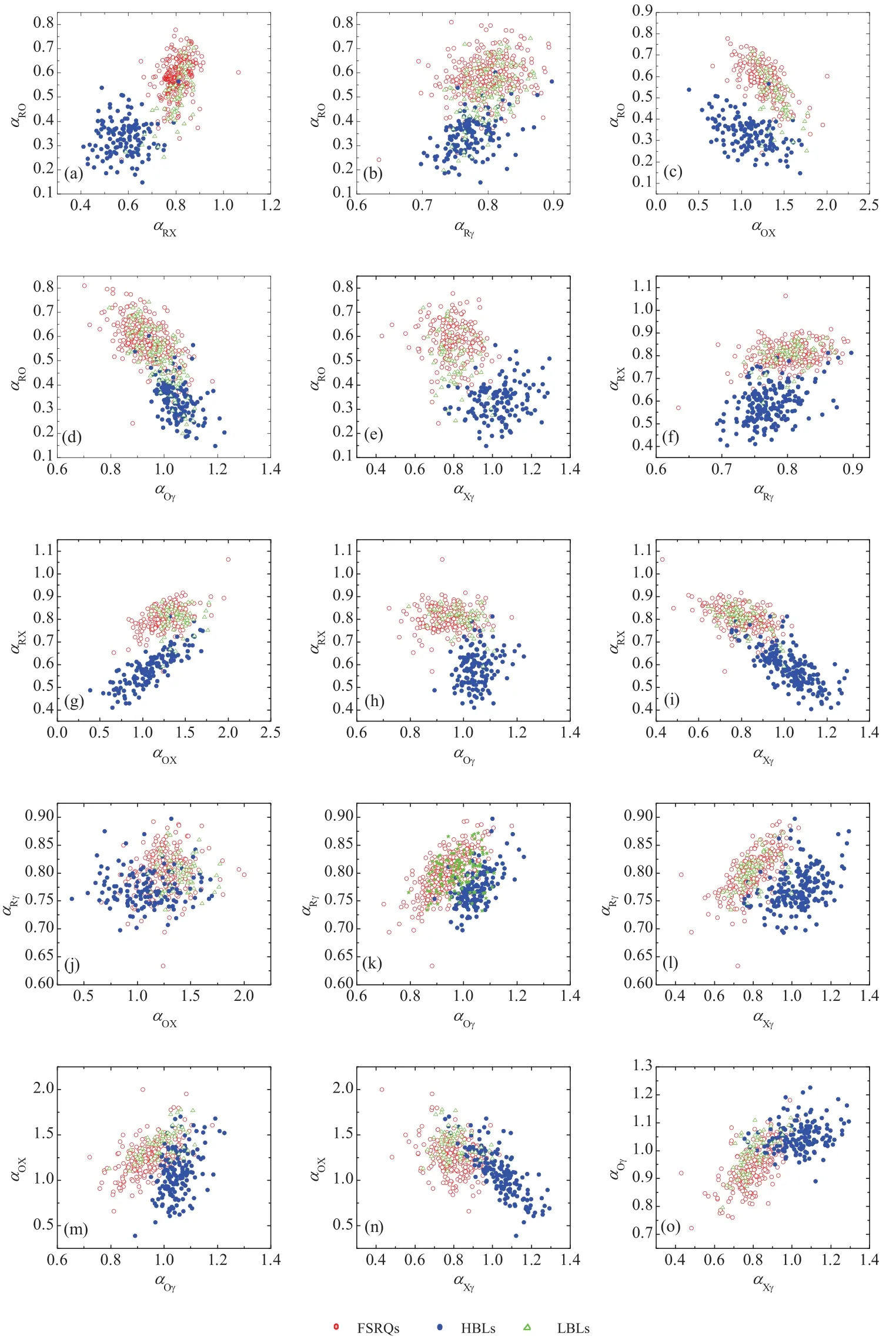
图1 任意2个有效谱指数之间的关系Fig.1 The correlations between any two effective spectral indices
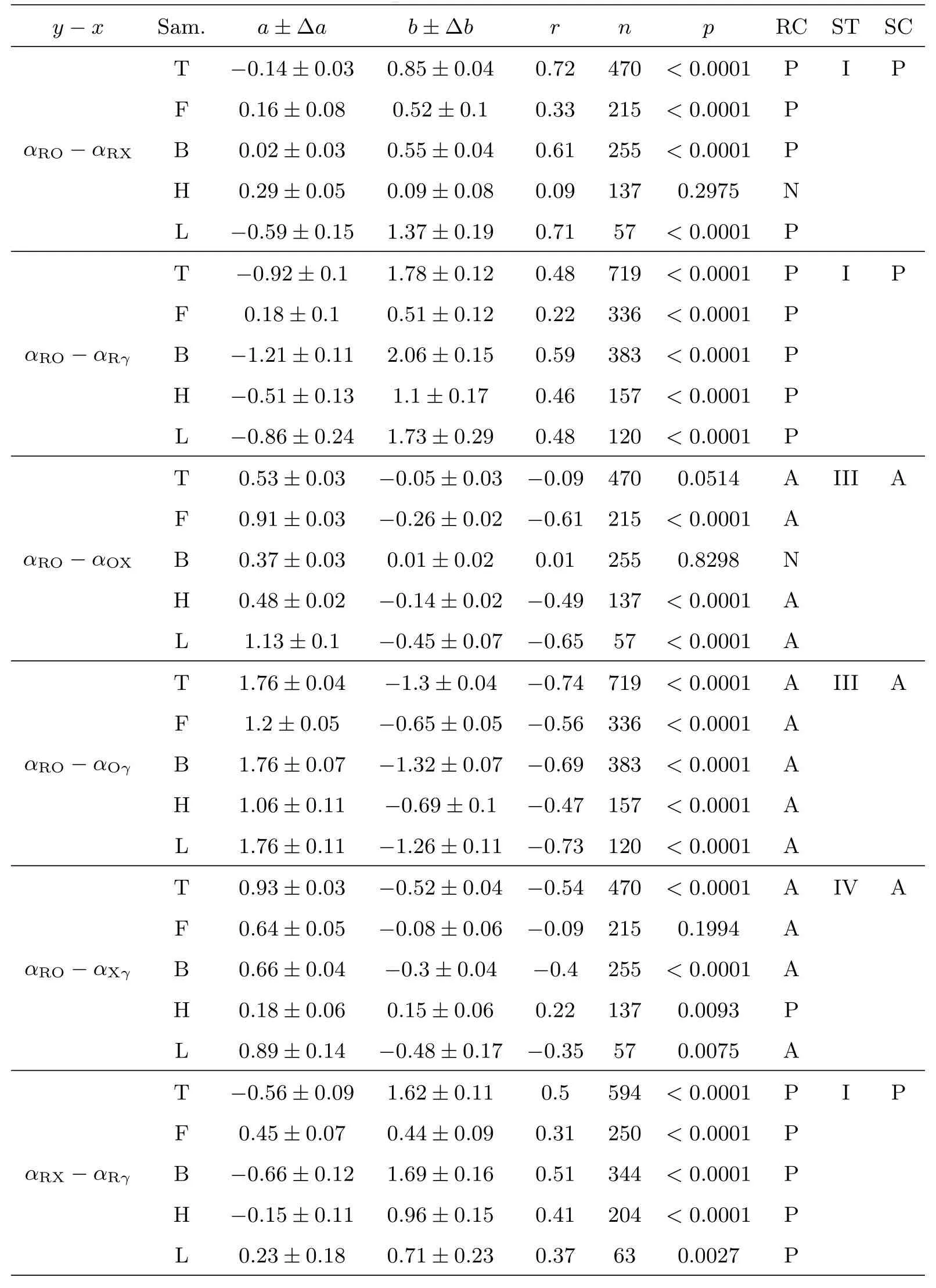
表2 任意2个有效谱指数之间相关的线性回归结果Table 2 The linear fitting results for the correlations between any two effective spectral indices
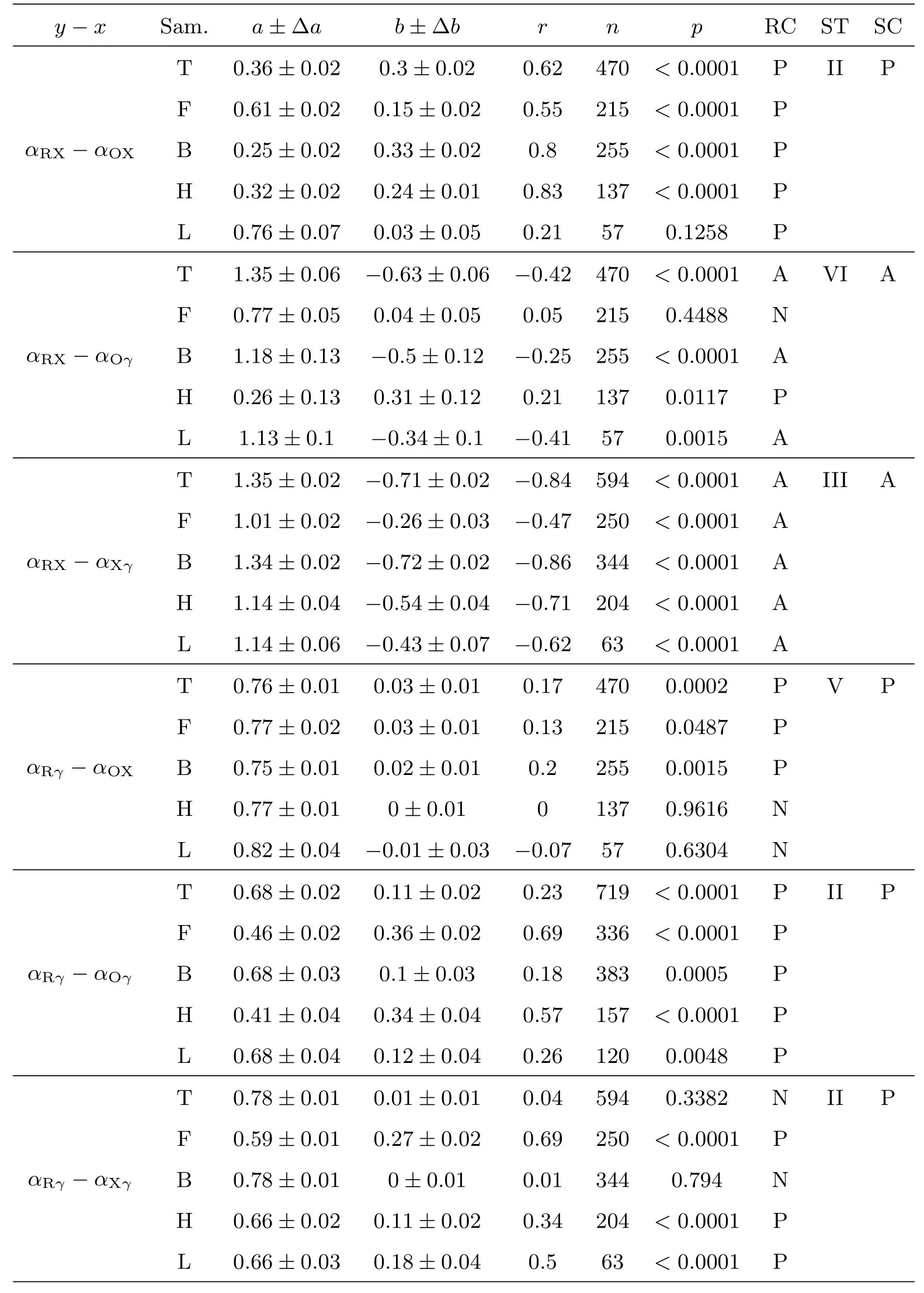
表2 续Table 2 Continued
表2 续Table 2 Continued
(6)对于T、F、B、L样本, αRO− αXγ有反相关或反相关趋势; 对于H样本, αRO−αXγ有弱正相关关系;
(7)对于T、B、L样本, αRX− αOγ存在反相关; 对于H样本, 其呈弱正相关; 对F样本, 其无相关;
(8)对于T、F、B样本, αRγ−αOX存在较弱的正相关; 对于H和L样本, αRγ−αOX无相关.
以上这些相关性汇总于表2第8列中.综上, 除了少数例外, 上述15对关系中, αRO−αRX, αRO− αRγ, αRX− αRγ, αRX− αOX, αRγ− αOX, αRγ− αOγ, αRγ− αXγ, αOX−αOγ及αOγ− αXγ存在正相关关系; αRO− αOX, αRO− αOγ, αRO− αXγ, αRX− αOγ,αRX−αXγ及αOX−αXγ存在反相关关系.
对于有效谱指数之间的关系, 一些文献用不同的样本进行了研究, 特别是αRO−αOX的关系讨论较多[1–3,6–8,10–11].Donato等[7]讨论了αRO与αRX、αOX和αRX之间的关系; Dondi等[8]讨论了αRO− αOγ、αRO− αXγ的关系; Zheng等[11]还讨论了αOγ− αRO、αXγ− αRX、αir,X− αR,ir、αOγ− αRO的关系, αir,X和αR,ir分别为红外到X-ray与射电到红外的有效谱指数关系.比较发现, 本文结果与以上文献结果的差异主要体现在相关程度上.相关程度上的差异应该是由样本量不同所导致, 因此文献所给出的有效谱指数之间的关系存在选择效应.由于本文所用样本量远大于上述工作所用的样本量, 因此本文结果应有更高的可信度.
4.2 从流量密度随频率的变化看2个有效谱指数的关系
某源在射电、光学、X-ray和γ-ray波段的流量密度对数值(lgfν)与频率对数值(lgν)之间的关系如图2所示.根据有效谱指数的定义(αij= −lg(fi/fj)/lg(νi/νj))可知, 图2中任意2点(R、O、X和G)连线斜率的负值就是该2点所代表频率之间的有效谱指数, 例如, −kRO=αRO等, 这里kRO为图2中RO连线的斜率.
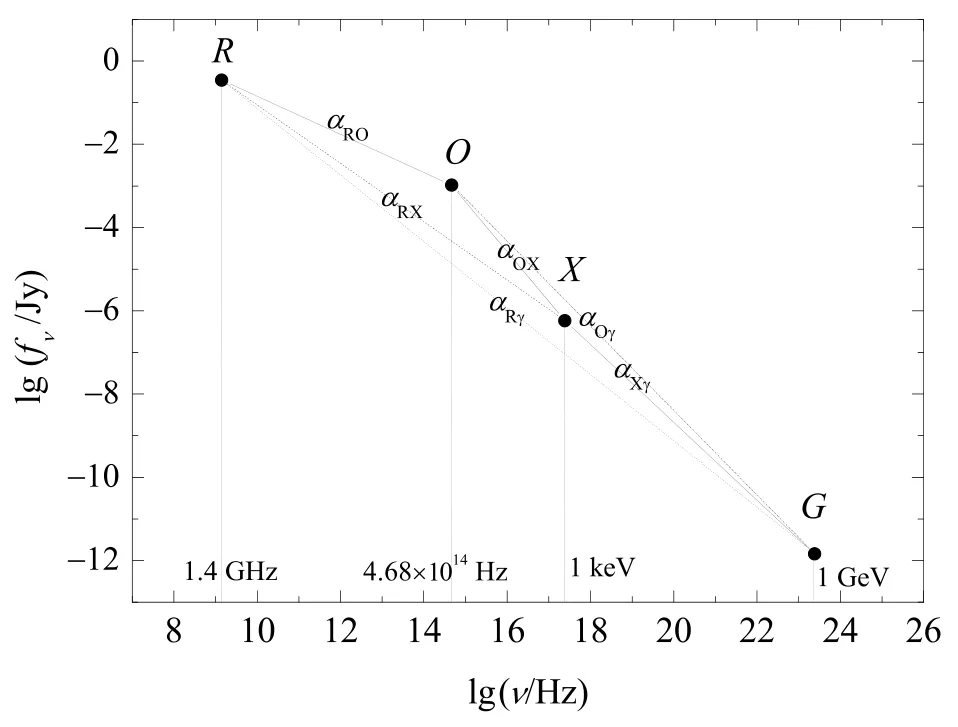
图2 某源在射电1.4 GHz、光学4.68×1014 Hz、X-ray 1 keV及γ-ray 1 GeV流量密度(lgf)与频率(lgν)的关系Fig.2 The correlation between flux densities and frequency of a certain source at radio 1.4 GHz, optical 4.68 × 1014 Hz, X-ray 1 keV, and γ-ray 1 GeV
按2个有效谱指数在图2中连线的位置, 从图2中15对有效谱指数各自的2条连线位置总结出6种结构类型如图3所示.αRO− αRX、αRO− αRγ、αRX− αRγ、αOX− αOγ的关系属于第I类结构(图3 (a)); αRX−αOX、αRγ−αOγ、αRγ−αXγ、αOγ− αXγ的关系, 属于第II类结构(图3 (b)); αRO− αOX、αRO− αOγ、αRX− αXγ、αOX− αXγ之间的关系属于第III类结构(图3 (c)); αRO− αXγ的关系属于第IV类结构(图3 (d)); αRγ− αOX的关系属于第V类结构(图3 (e)); αRX−αOγ的关系属于第VI类结构(图3 (f)).每一对有效谱指数的关系结构类型列于表2的第9列.对于IV、V和VI的结构类型(图3 (d, e, f)), 如果将2条线上相邻的2点视为1个点, 那么结构IV、V和VI将分别变为结构III、II (或I)和III(见图3 (d、e、f)中的小图).因此, 这些结构最终被统一为3种类型, 即I、II和III (图3(a、b、c)).
下面讨论在不同结构类型中2条线斜率, 即2个有效谱指数之间的相关.
对于结构I、II和III(图3(a、b和c)),A、B和C点的坐标分别为(lgνA,lgfνA)、(lgνB,lgfνB)和(lgνC, lgfνC).不同的源在相同频率处的流量密度不同, 对于某个blazar样本,所有源在同一频率下的流量密度有一定的变化范围, 但样本不同这个变化范围也将不同.也就是说, 不同类型的blazar样本(FSRQ, BL Lac, HBL, LBL)的lgfνA(或lgfνB,或lgfνC)在各自的范围内变化.大量研究表明, blazar多波段的辐射流量密度之间存在正相关关系[8,18−23].这意味着lgfνA, lgfνB和lgfνC中某1个流量增加, 那么其他2个也会相应地增加.
根据以上分析, 下面从数学上分析结构I、II和III (图3 (a、b、c))中2条直线斜率(2个有效谱指数)之间的变化关系.结构I (图3 (a)), 当lgfνA增加或减小时,αAB和αAC都将增加或减小, 这表明αAB和αAC之间存在正相关; 同样, 对于结构II (图3(b)), αCA和αBA之间存在正相关关系; 对于结构III (图3 (c)), 当lgfνA增加或减小时,αBA会减小或增加, αAC会增加或减小, 因此αBA和αAC之间应存在反相关关系.根据这种结构类型关系,15对有效谱指数关系中,αRO−αRX,αRO−αRγ,αRX−αRγ,αRX−αOX,αRγ −αOX, αRγ−αOγ, αRγ−αXγ, αOX−αOγ及αOγ−αXγ应有正相关关系; αRO−αOX,αRO − αOγ, αRO− αXγ, αRX− αOγ, αRX− αXγ及αOX− αXγ应有反相关关系.
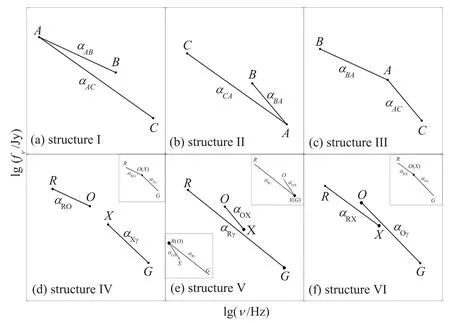
图3 有效谱指数的关系结构Fig.3 The relational structure of effective spectral indices
表2的第9列和第10列给出了2个谱指数之间相关性的结构类型及结构类型所指示的相关性, 第8列总结了从线性回归中得到的相关性.通过比较这两个结果, 除了少数例外, 可以发现这两个结果基本上是一致的.少数例外主要是总样本、BL Lac样本, 还有HBL样本的少量谱指数之间的相关以及αRγ与αOX之间的相关.
关于总样本及BL Lac样本的例外, 主要是因为这两类样本中都包含有几个子类样本, 从这些样本的谱指数关系的散点图可见, 子类样本FSRQ (LBL)与HBL各自分布方向与这两类样本的分离方向不同, 这种分布方向与分离方向的不同造成了总样本及BL Lac样本的一些谱指数之间的关系减弱或无相关.如αRO−αOX(图1 (c)), HBL与FSRQ(LBL)在图中的分布方向都是从左上向右下分布, 但HBL与FSRQ (LBL) 2类之间是从左下向右上分开, 且较明显, 这样就导致了子类样本都有强的反相关, 但总样本及BL Lac样本的αRO−αOX却没有相关.
αRγ−αOX(图1 (j))的关系结构类型属于V (或I和II), 结构关系表明它们之间应存在正相关.拟合结果显示, 不同blazar样本仅显示了弱的正相关或根本没有相关.事实上, 由于R到G的频率差很大(lg[(νγ/νR)]= 14.24), 导致lgfR或lgfγ的变化, 引起αRγ的变化不明显, 另外, O离X 较近(lg[(νO/νX)]= 2.71), 小的流量变化就会引起有效谱指数αOX较大的变化, 2者综合作用下, 导致了αRγ与αOX之间仅存在弱的相关或根本没有相关.这种有效谱指数两点之间的最大频率差和最小频率差也导致了αRγ有最小标准偏差(σ =0.03 − 0.04)和αOX有最大的标准偏差(σ =0.16 − 0.29)[24].
HBL样本的αRO−αRX、αRO−αXγ、αRX−αOγ关系的拟合结果与结构关系不一致,且有较大的差异.可能是因为HBL的射电流量变化范围最小、光学流量与X-ray流量的相关性较差以及HBL的射电流量与γ-ray流量相关性最强所致.射电和γ-ray都是强束流,都有很强的集束效应, HBL的射电与γ-ray辐射相关性最强暗示HBL的射电和γ-ray辐射机制高度关联, 那么, 若射电辐射来自同步辐射(SC), 则HBL的γ-ray辐射应主要来自同步自康普顿辐射(SSC).
4.3 用多波段有效谱指数的关系区分HBL与FSRQ
从图1可以看出, FSRQ与LBL位于几乎相同的区域, 而HBL与FSRQ (LBL)彼此分离, 分别位于不同的区域, 但在不同的有效谱指数关系图中, 彼此分离程度(区分度)不同.因此, FSRQ与LBL或许有类似的辐射机制, 而HBL的辐射机制应与它们有所区别.
为了弄清在不同有效谱指数关系图中HBL与FSRQ的分离程度(区分度), 我们根据HBL与FSRQ在图中的分布, 统计了各图中HBL与FSRQ分布重叠部分源的数量(m);计算了任意2个有效谱指数之间的频率范围差(∆ν); 最后讨论了两类样本的重合度(m/N)与频率范围差(∆ν)的关系, m为重叠部分源的数量, N为FSRQ与HBL的样本量之和.下面说明两个有效谱指数之间的频率范围差(∆ν)的计算方法,以计算αRγ与αOX的频率范围差为例: 已知νR= 1.4 × 109Hz、νγ= 2.42 × 1023Hz、νO= 4.68 ×1014Hz、νX=2.42 × 1017Hz,定义∆lgν(αRγ)=lg(νγ/νR)=14.24,同样∆lgν(αOX)=lg(νX/νO) = 2.71, 则有效 谱 指数αRγ与αOX之间 的 频率范 围 差∆ν(αRγ,αOX) =∆lg ν(αRγ) − ∆lgν(αOX)=14.24 − 2.71=11.53.
根据以上分析,得到15对有效谱指数关系的m/N −∆ν关系如图4所示.m/N −∆ν关系的线性拟合结果为相关系数r =0.71, 机会概率p= 0.28%.因此, m/N −∆ν之间存在正相关关系, 也就是说两个有效谱指数之间的频率范围差越小, HBL与FSRQ在图中的区分度越高.因此, 应可用合适的有效谱指数关系对HBL和FSRQ进行区分.
5 结论
本文以3FGL为基础样本, 计算了射电到光学、射电到X-ray、射电到γ-ray、光学到X-ray、光学到γ-ray和X-ray到γ-ray的有效谱指数.讨论了任意2个有效谱指数之间的关系, 得到以下主要结论:
(1)除了少数例外, 6个有效谱指数两两之间的15对关系的拟合结果显示: αRO−αRX、αRO− αRγ、αRX− αRγ、αRX− αOX、αRγ− αOX、αRγ− αOγ、αRγ− αXγ、αOX−αOγ及αOγ−αXγ存在正相关关系;αRO−αOX、αRO−αOγ、αRO−αXγ、αRX−αOγ、αRX−αXγ及αOX− αXγ存在反相关关系;
(2)根据流量密度的能谱分布给出了任意2个有效谱指数相关的几种结构类型, 每种结构类型指向一种相关关系.比较发现, 结构类型指示的某2个有谱指数的相关性与拟合给出的相关性, 除了少数例外, 是一致的;
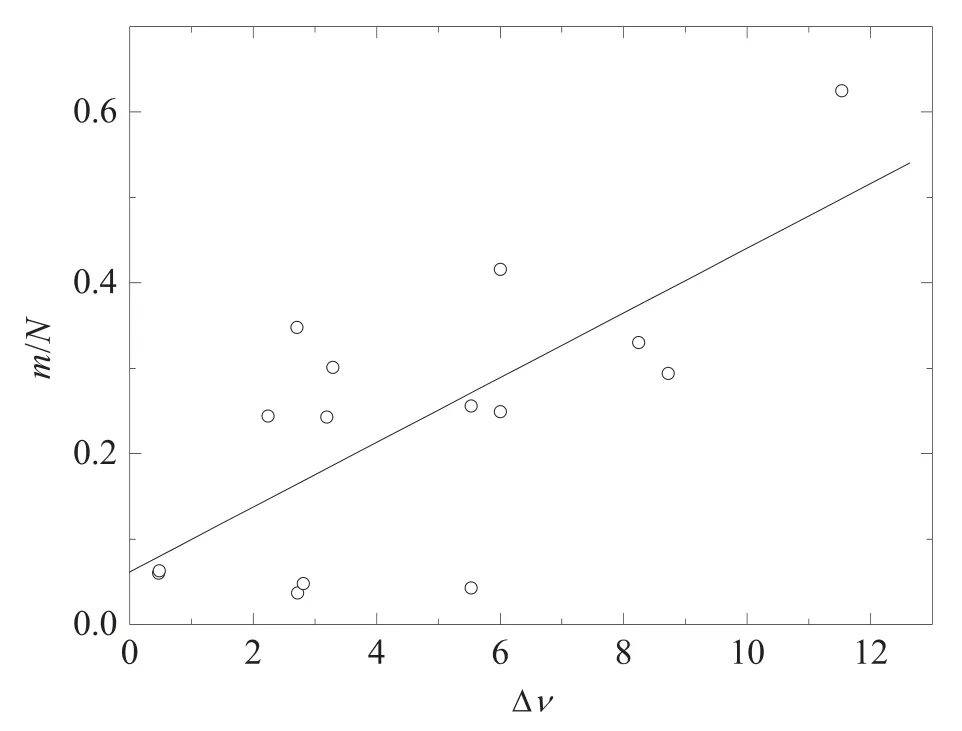
图4 m/N与∆ν的关系Fig.4 The relation between m/N and ∆ν
(3) HBL的γ-ray的辐射应主要来自同步自康普顿辐射过程;
(4)在大部分2个有效谱指数之间的相关图中, HBL与FSRQ位于完全分开的区域,而LBL与FSRQ位于相同的区域.暗示HBL与FSRQ (LBL)有不同的观测性质, FSRQ与LBL或许有类似的辐射机制;
(5)在有效谱指数之间关系的散点图中, HBL和FSRQ的区分度与两个有效谱指数之间的频率范围差存在反相关关系, 即频率差越小, 区分度越高.因此, 可寻找合适的两个有效谱指数来区分HBL和FSRQ.
致谢在本文的数据收集和处理工作中得到了湖南文理学院“电子科学与技术”、湖南省应用特色学科和洞庭湖生态经济区建设与发展协同创新中心的经费支持, 特此表示感谢!
附录
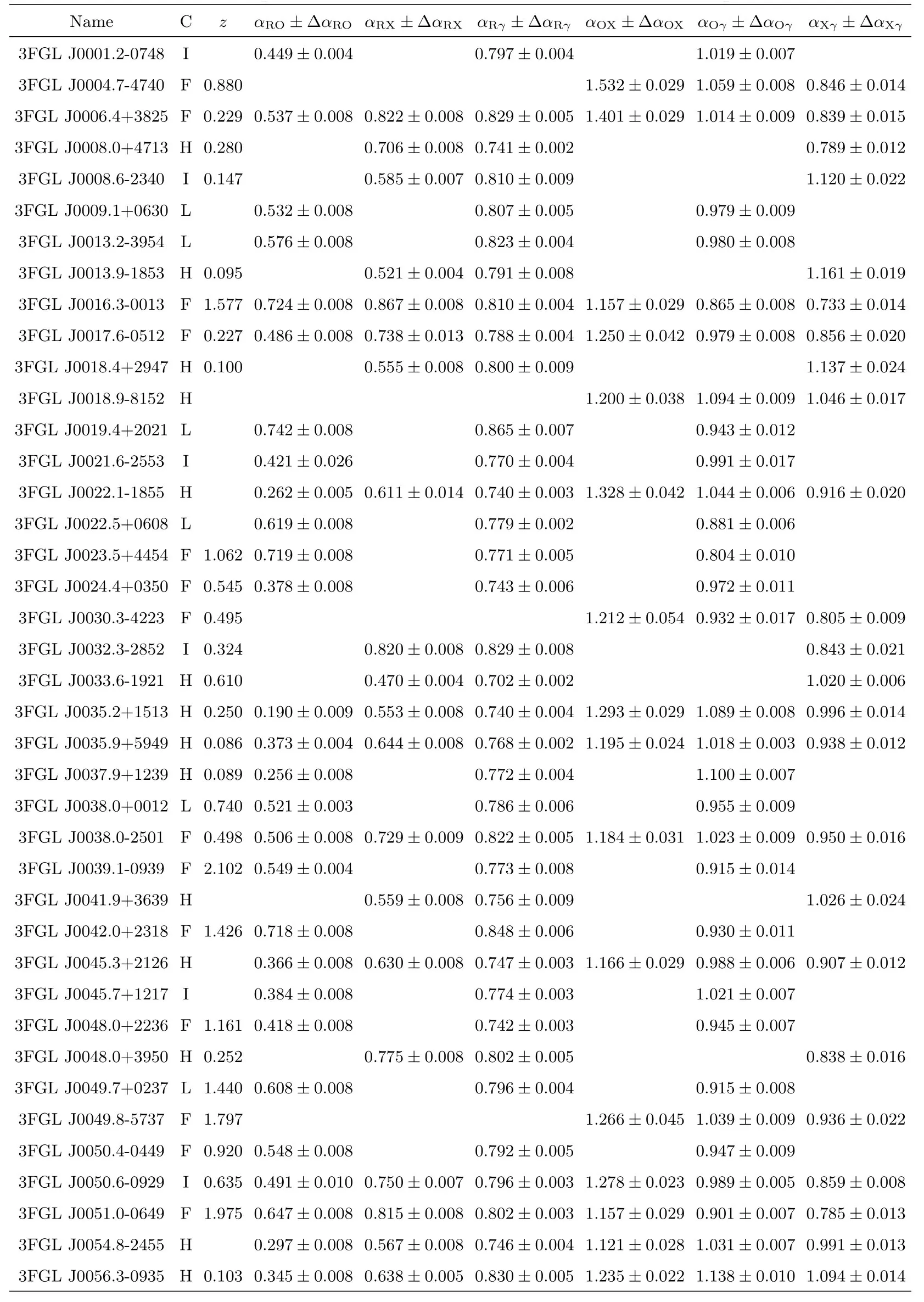
表3 样本及有效谱指数计算结果Table 3 Blazars sample and the calculation results of effective spectral indices
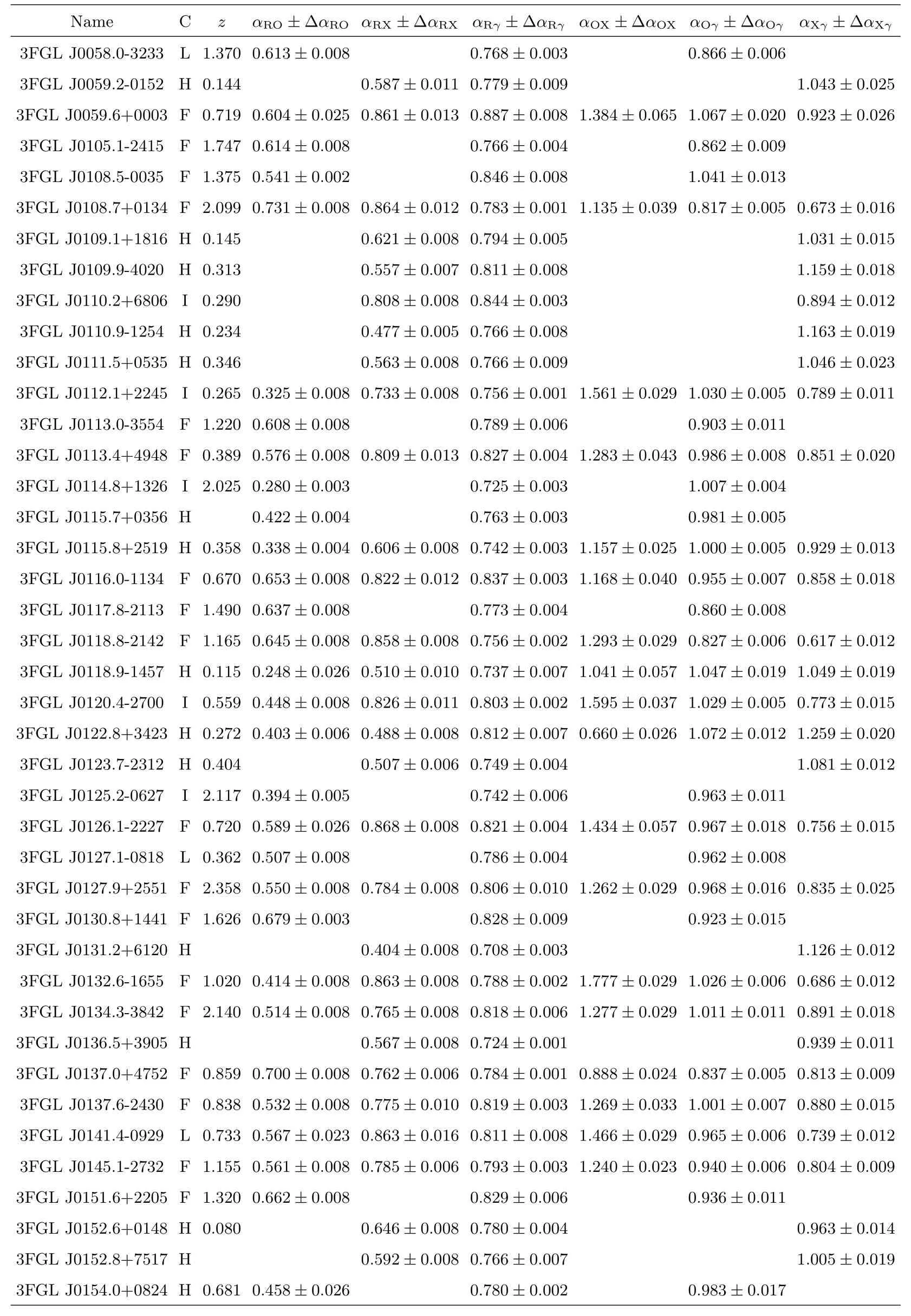
表3 续Table 3 Continued
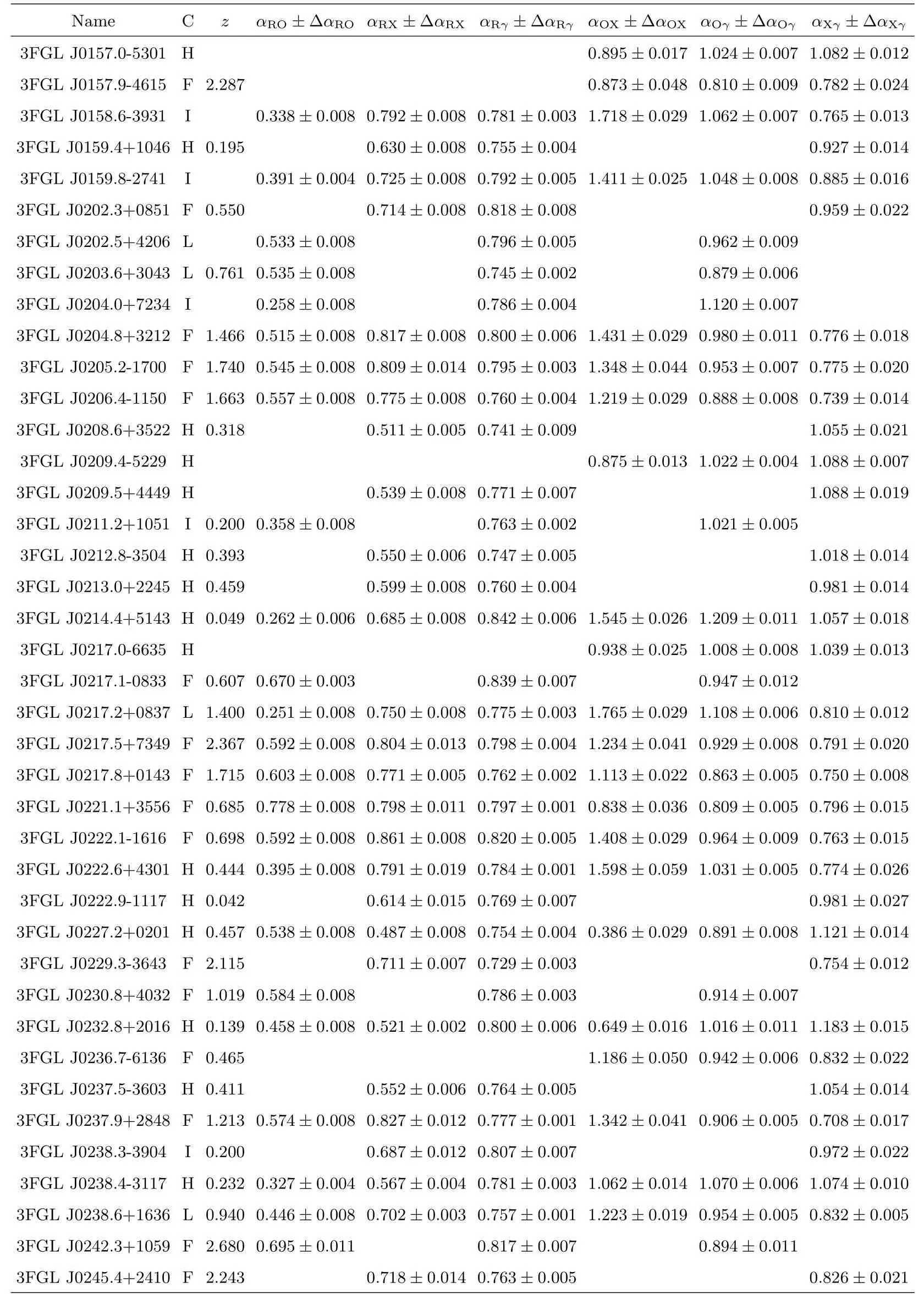
表3 续Table 3 Continued
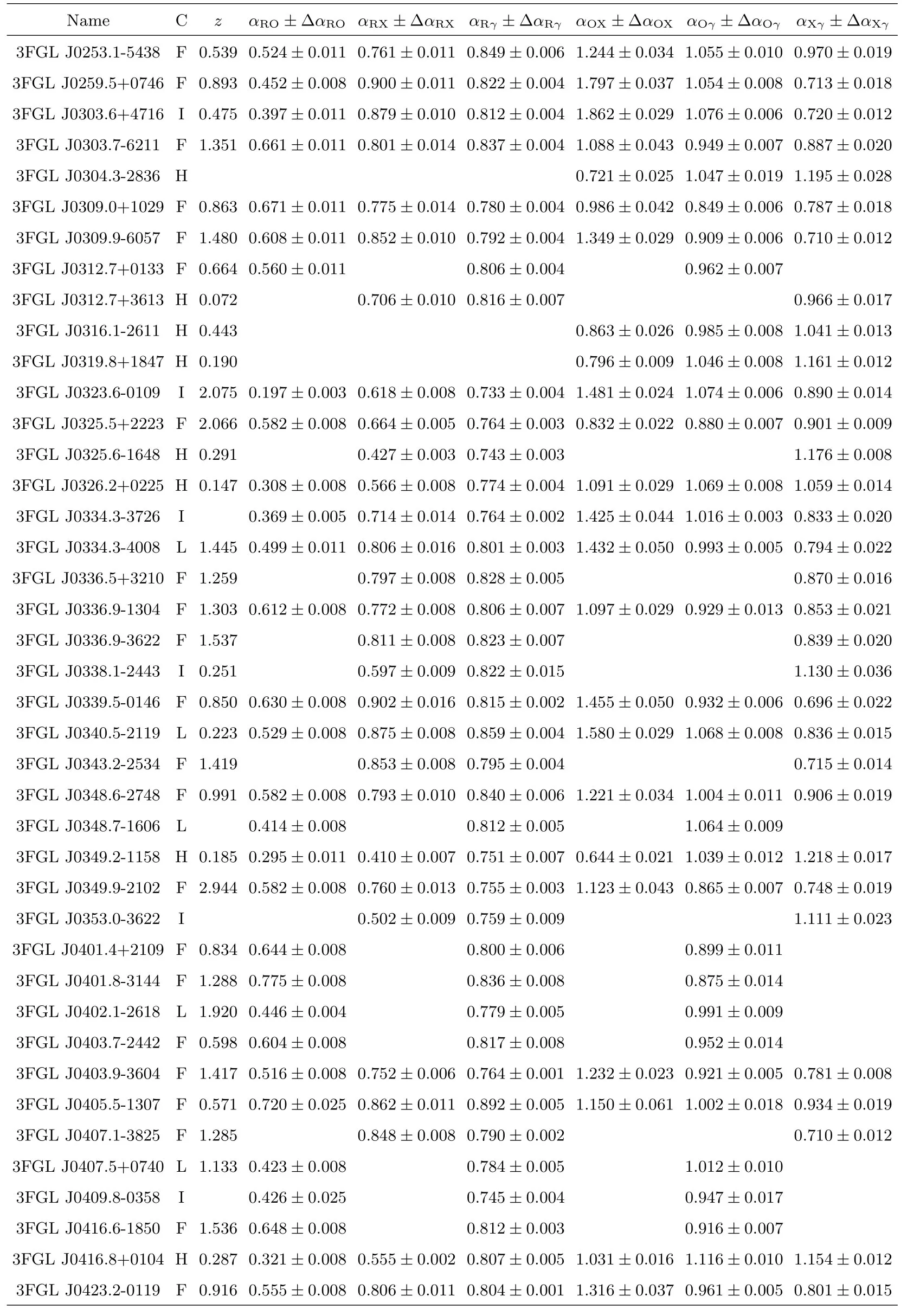
表3 续Table 3 Continued
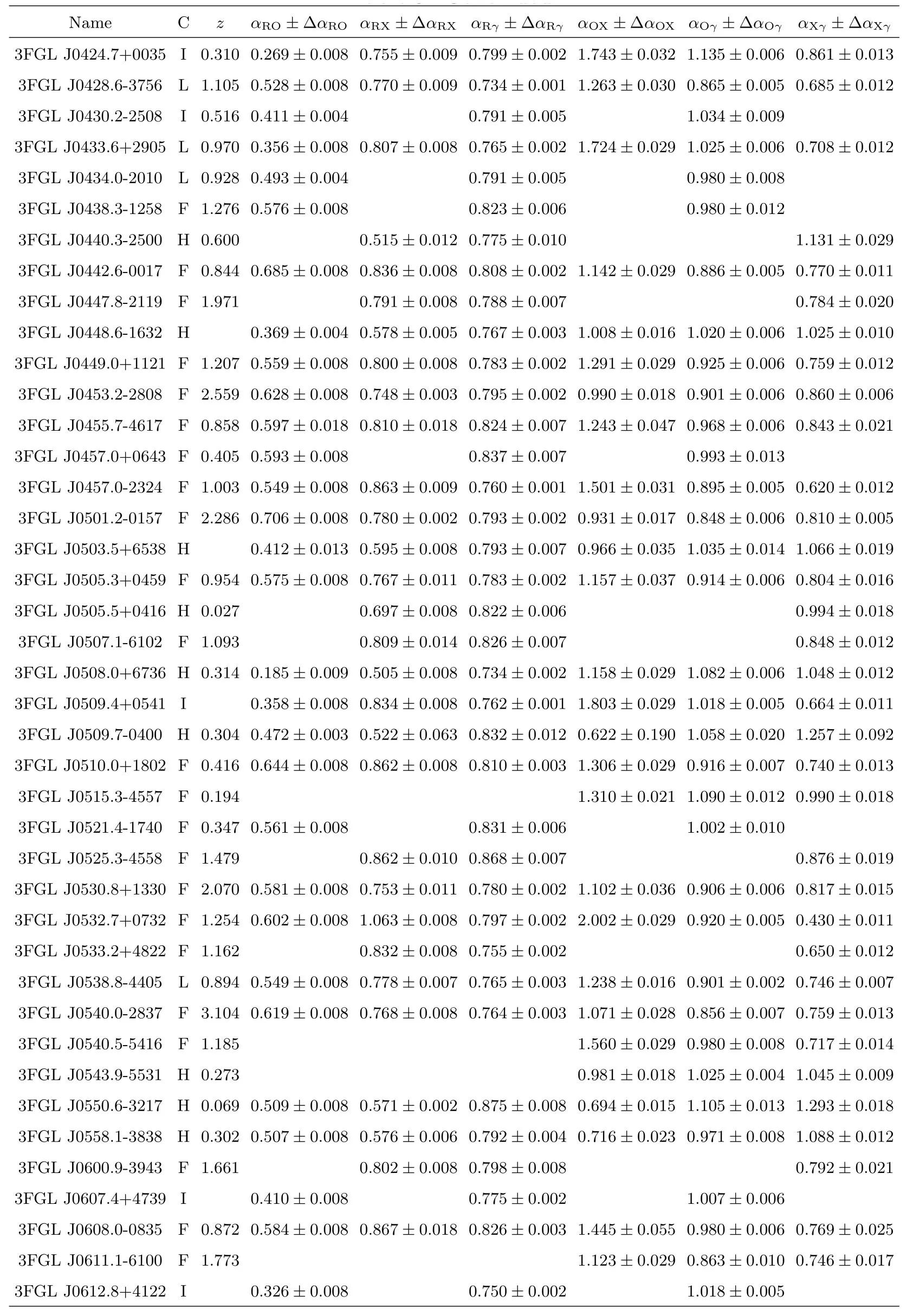
表3 续Table 3 Continued
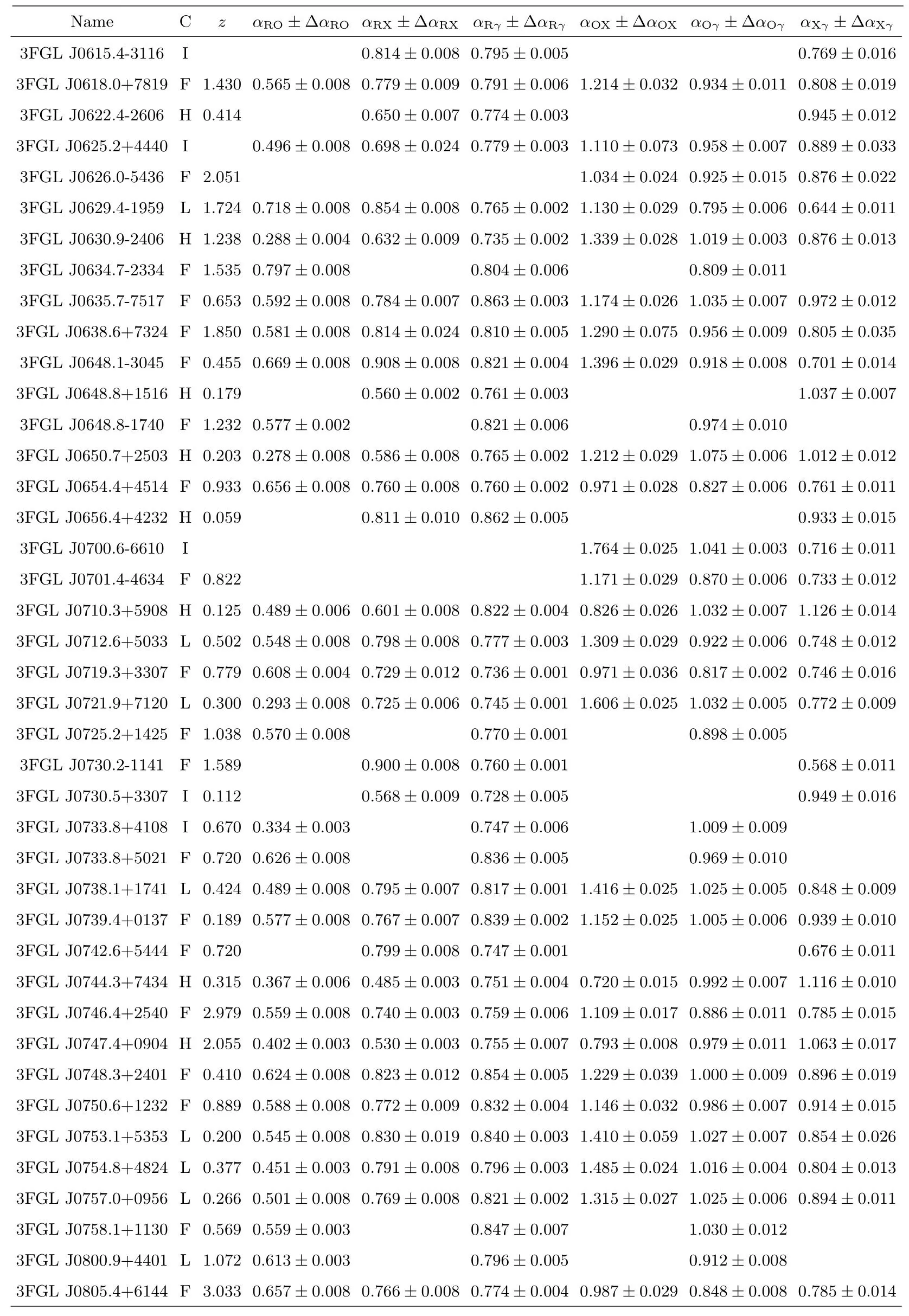
表3 续Table 3 Continued
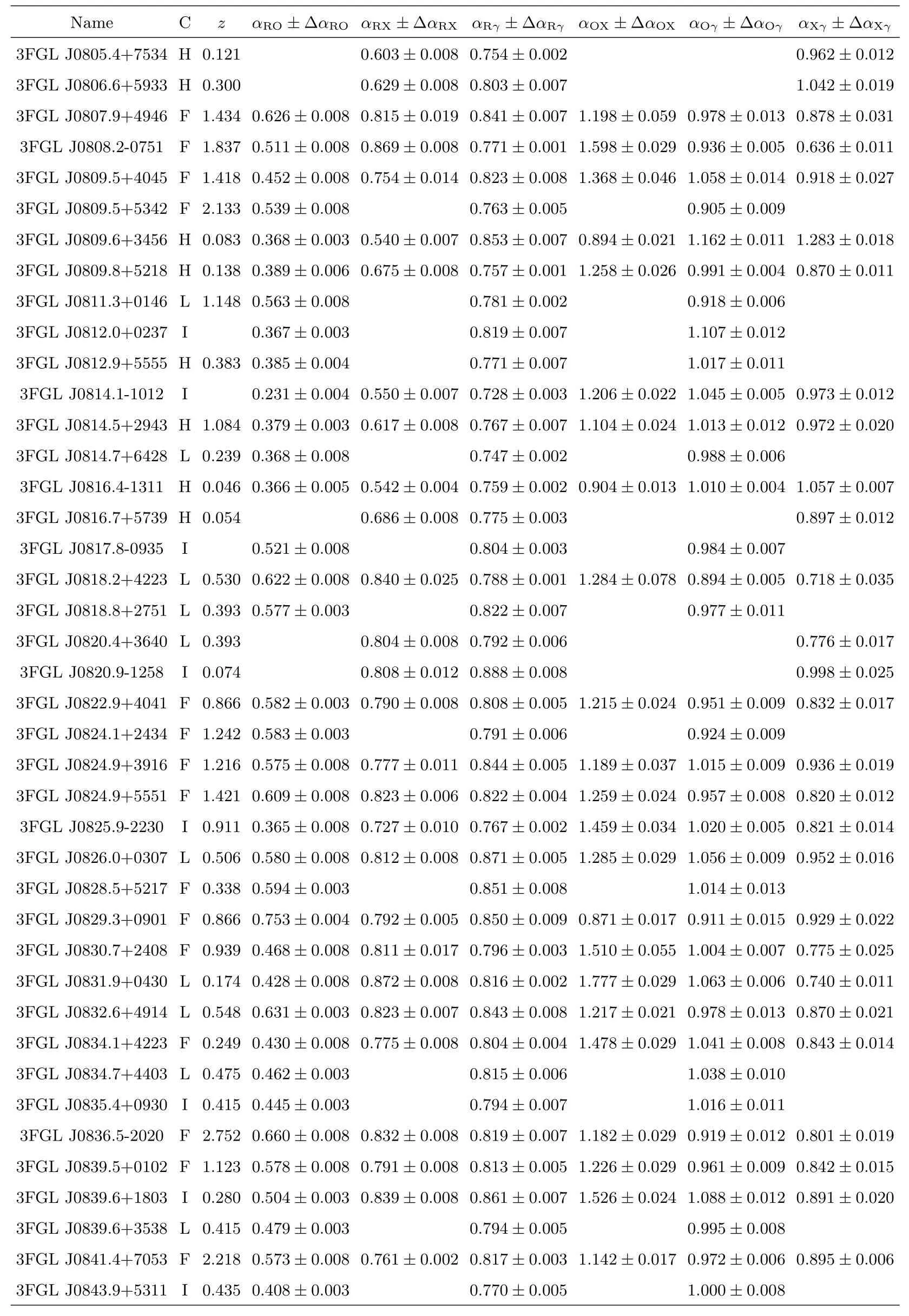
表3 续Table 3 Continued
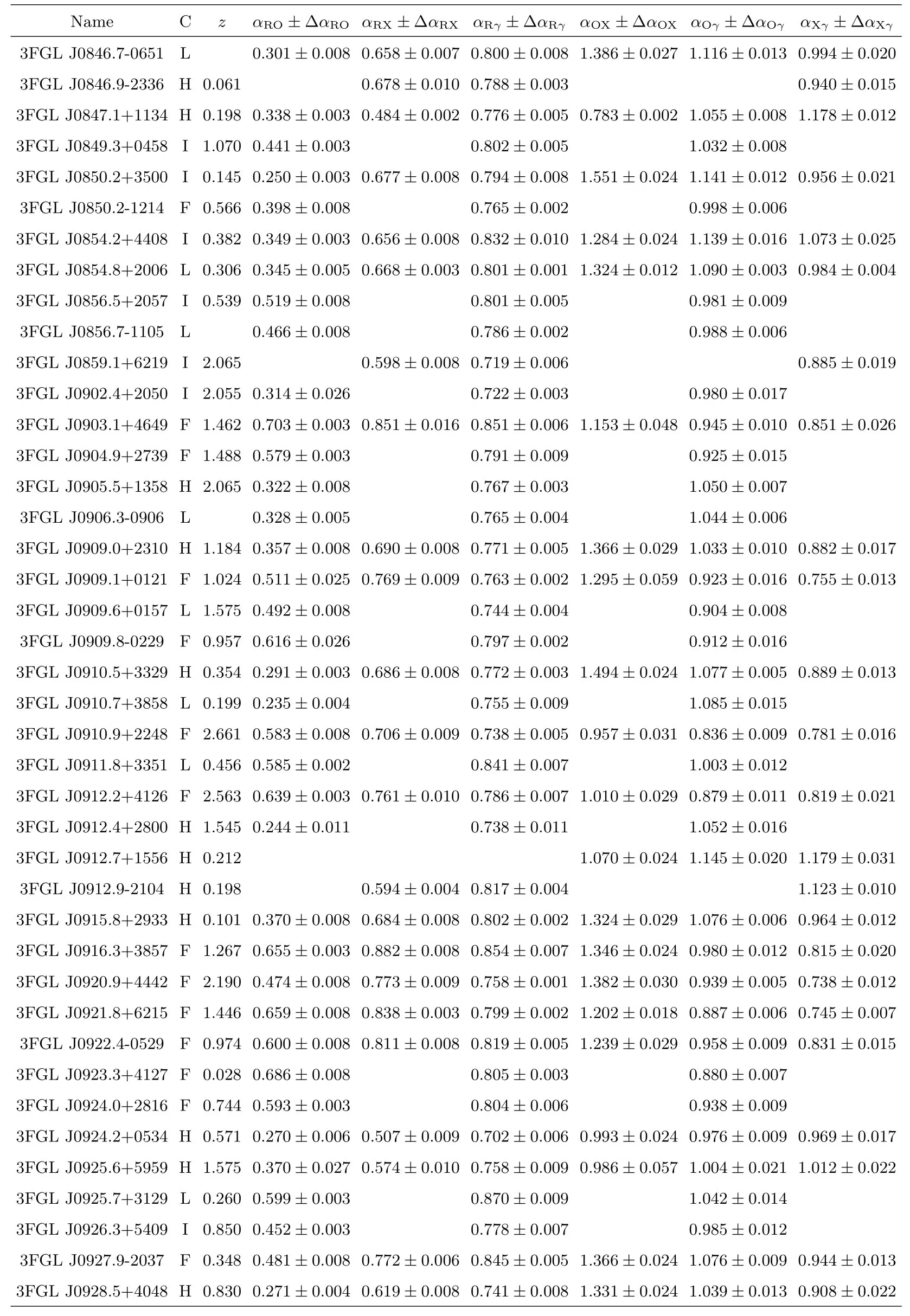
表3 续Table 3 Continued
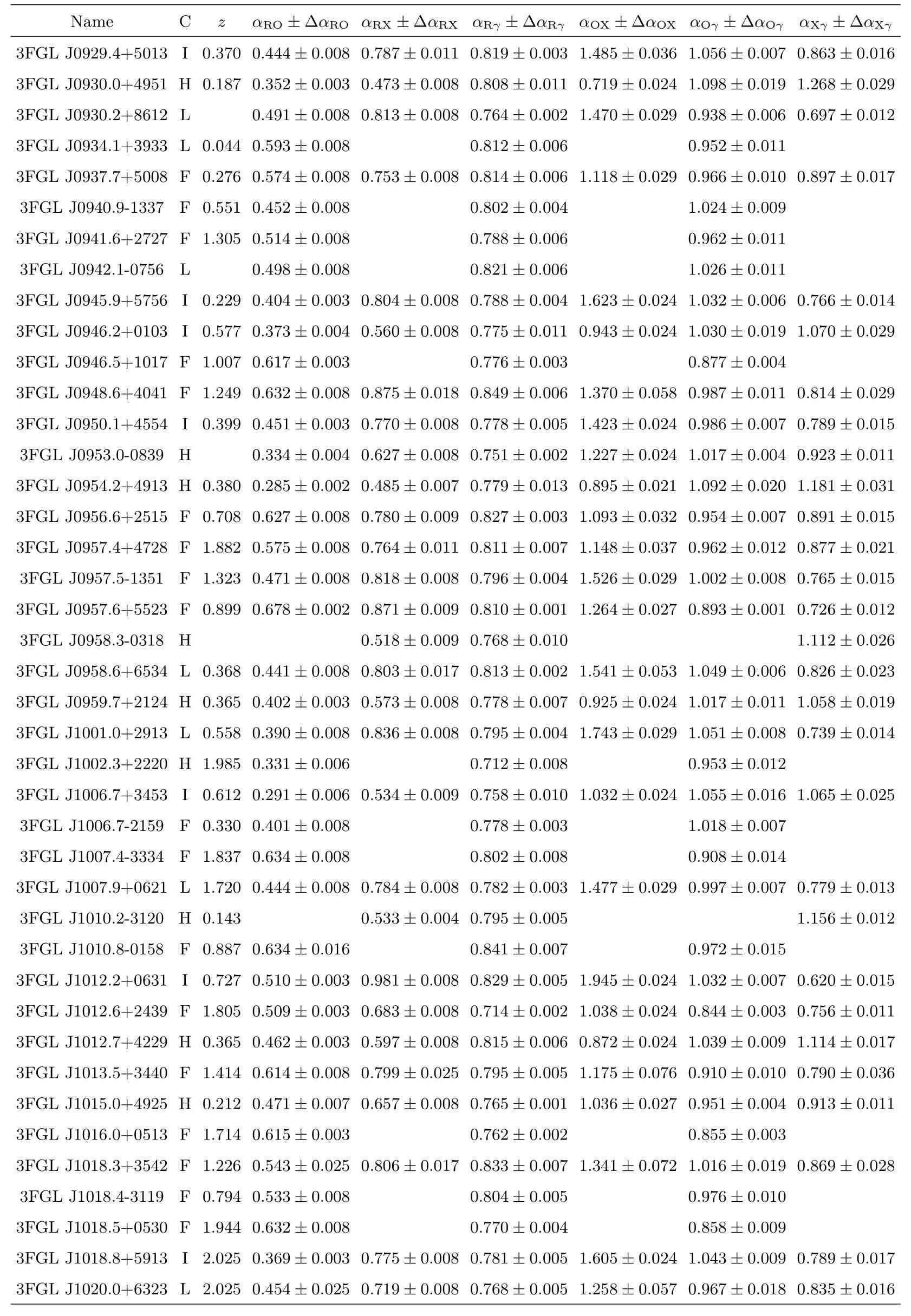
表3 续Table 3 Continued
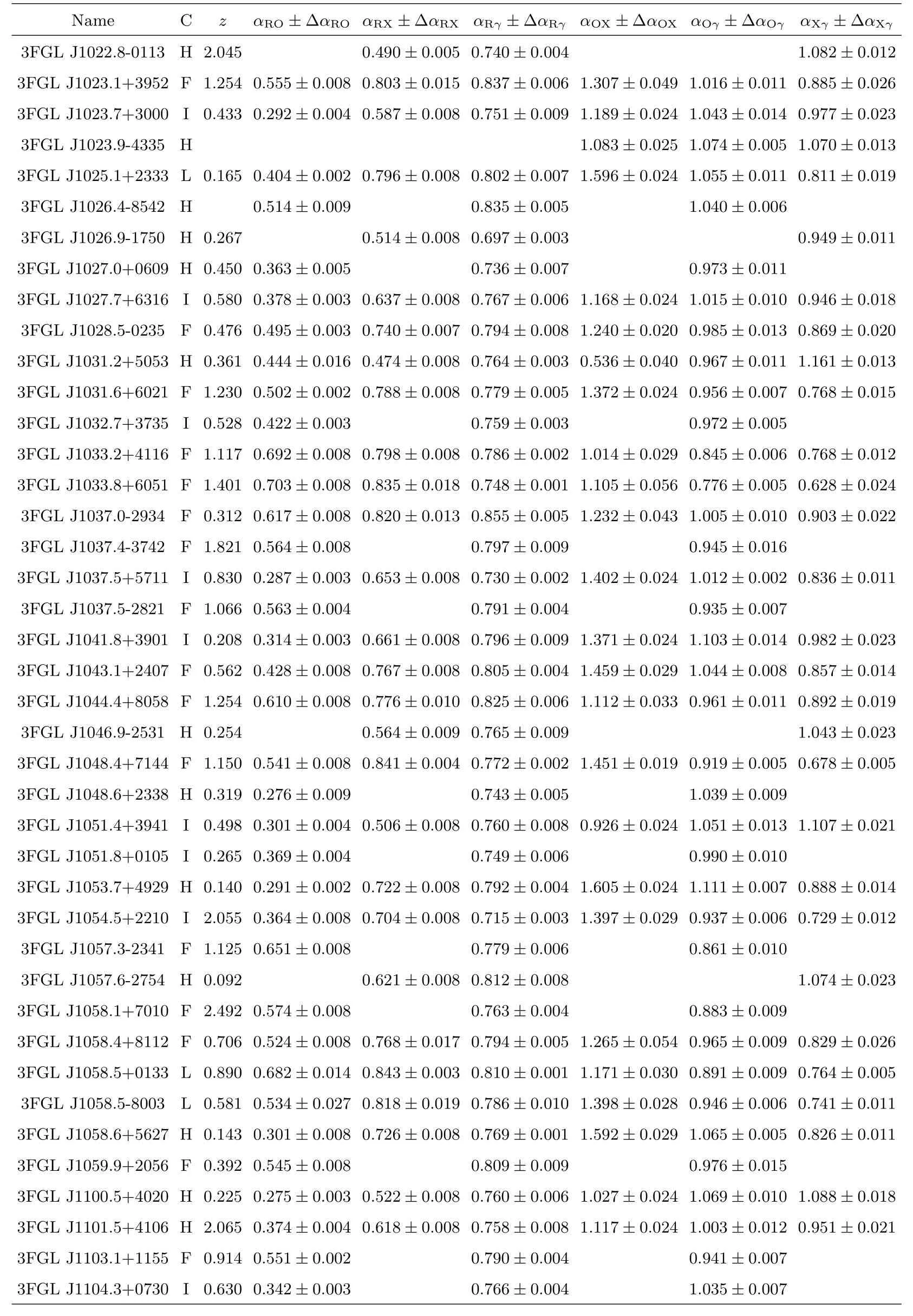
表3 续Table 3 Continued

表3 续Table 3 Continued
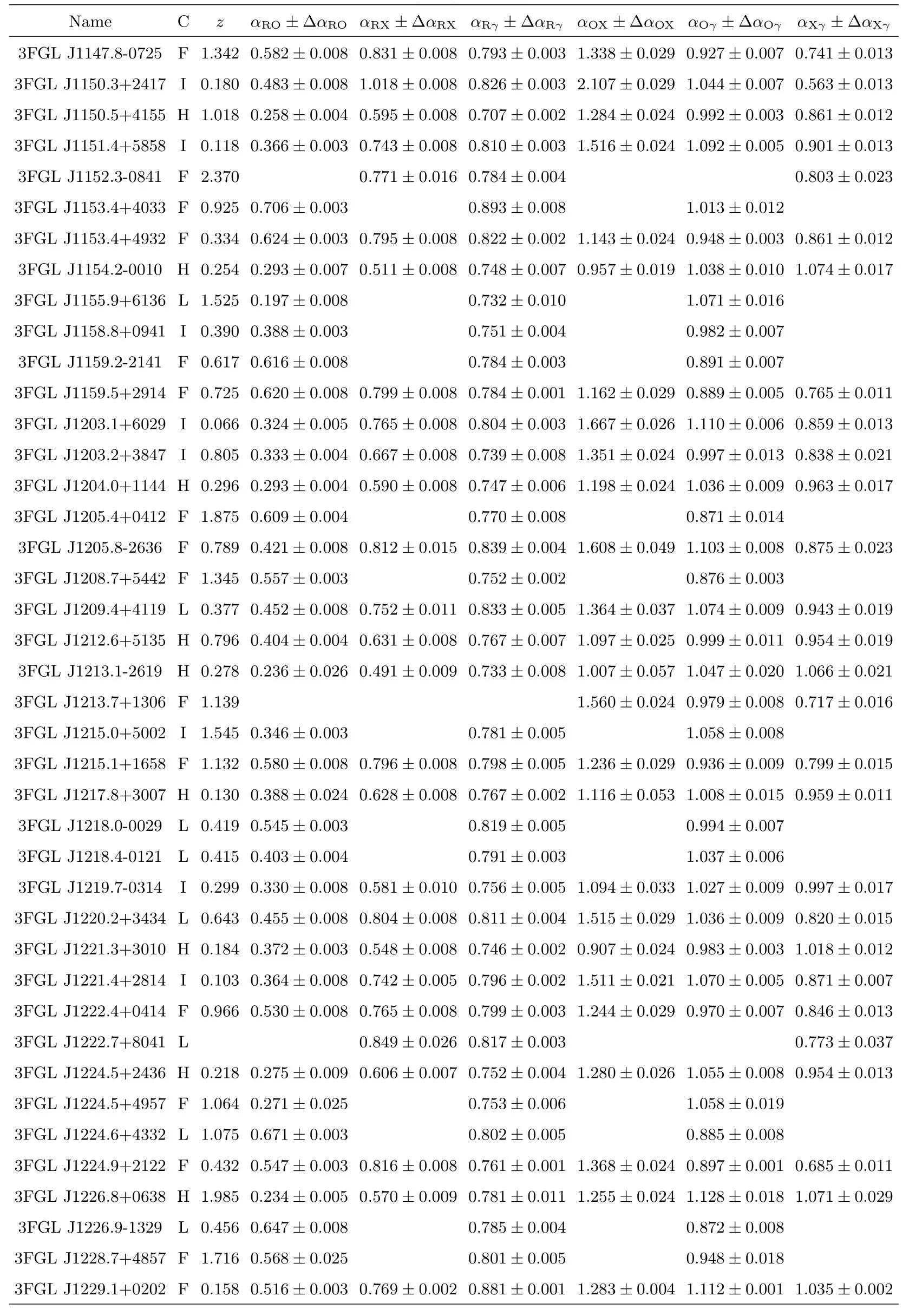
表3 续Table 3 Continued

表3 续Table 3 Continued
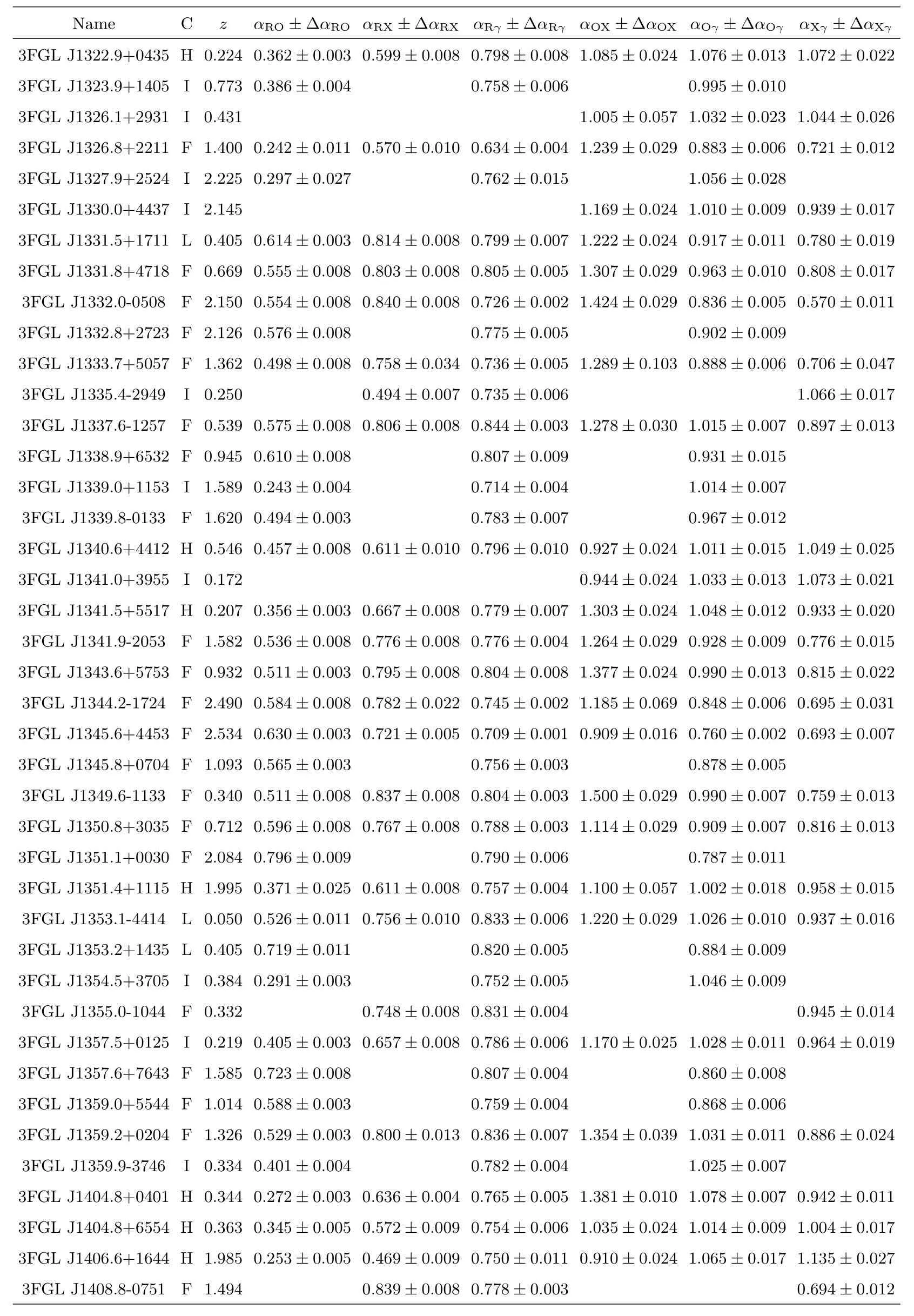
表3 续Table 3 Continued
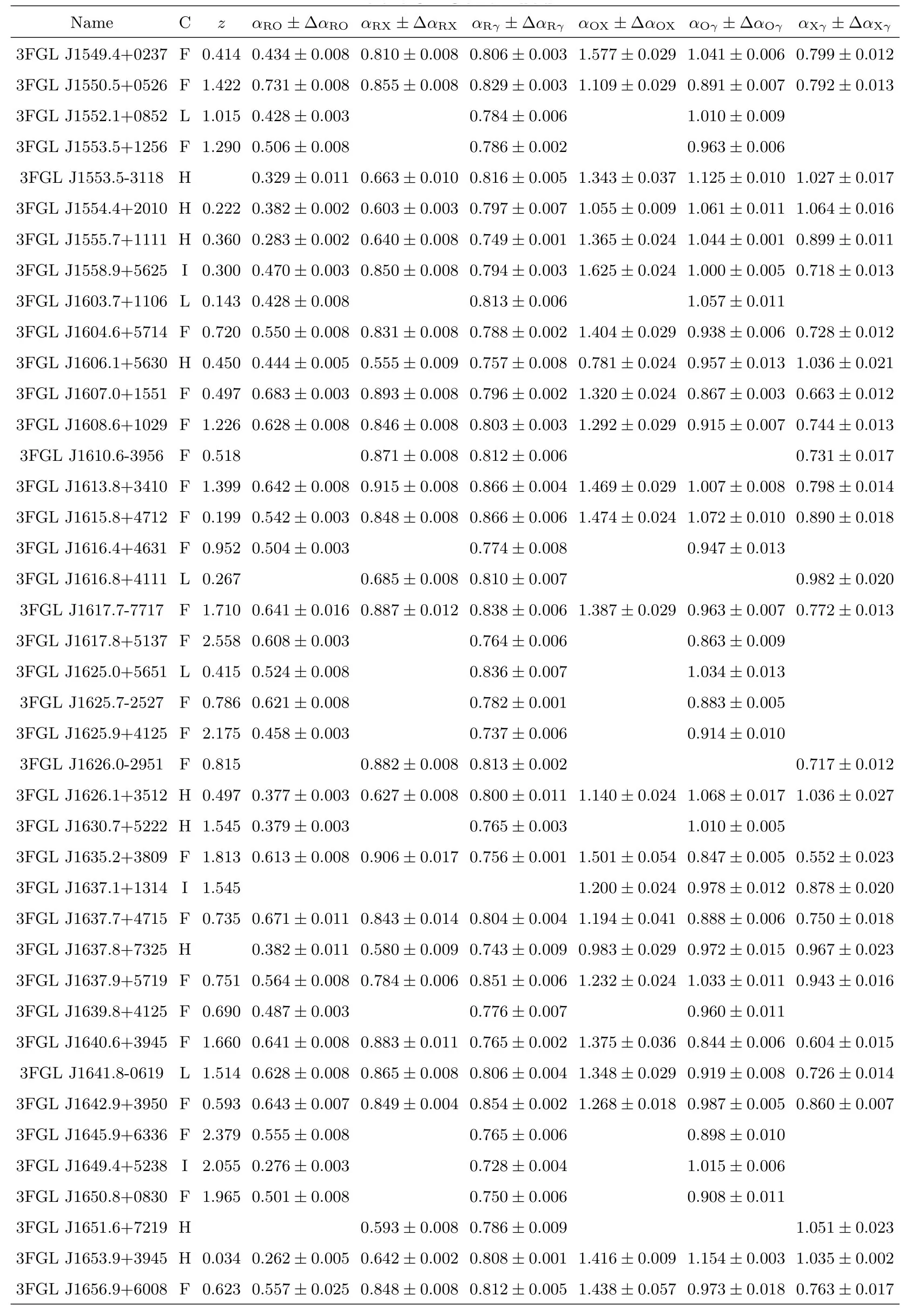
表3 续Table 3 Continued

表3 续Table 3 Continued
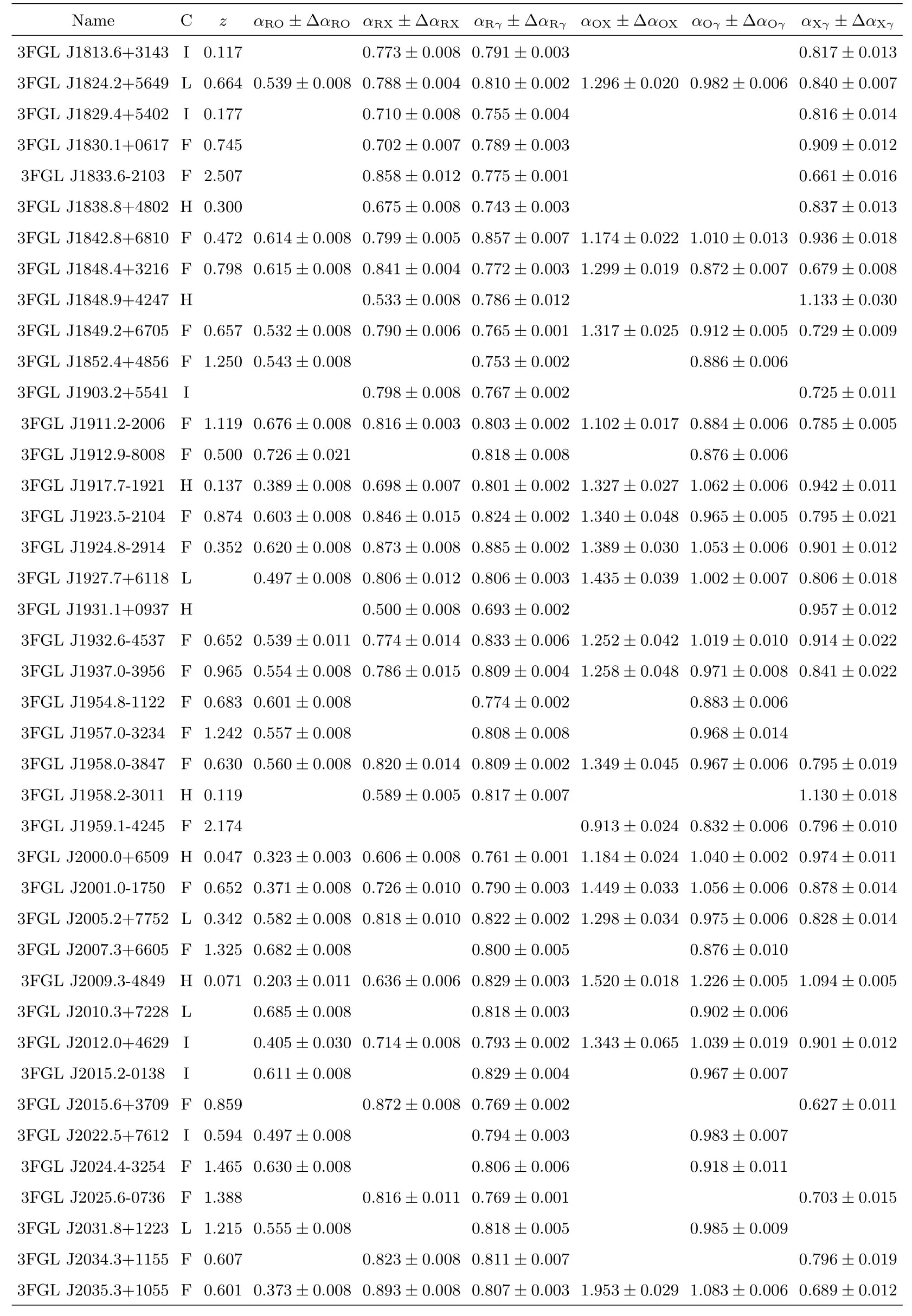
表3 续Table 3 Continued
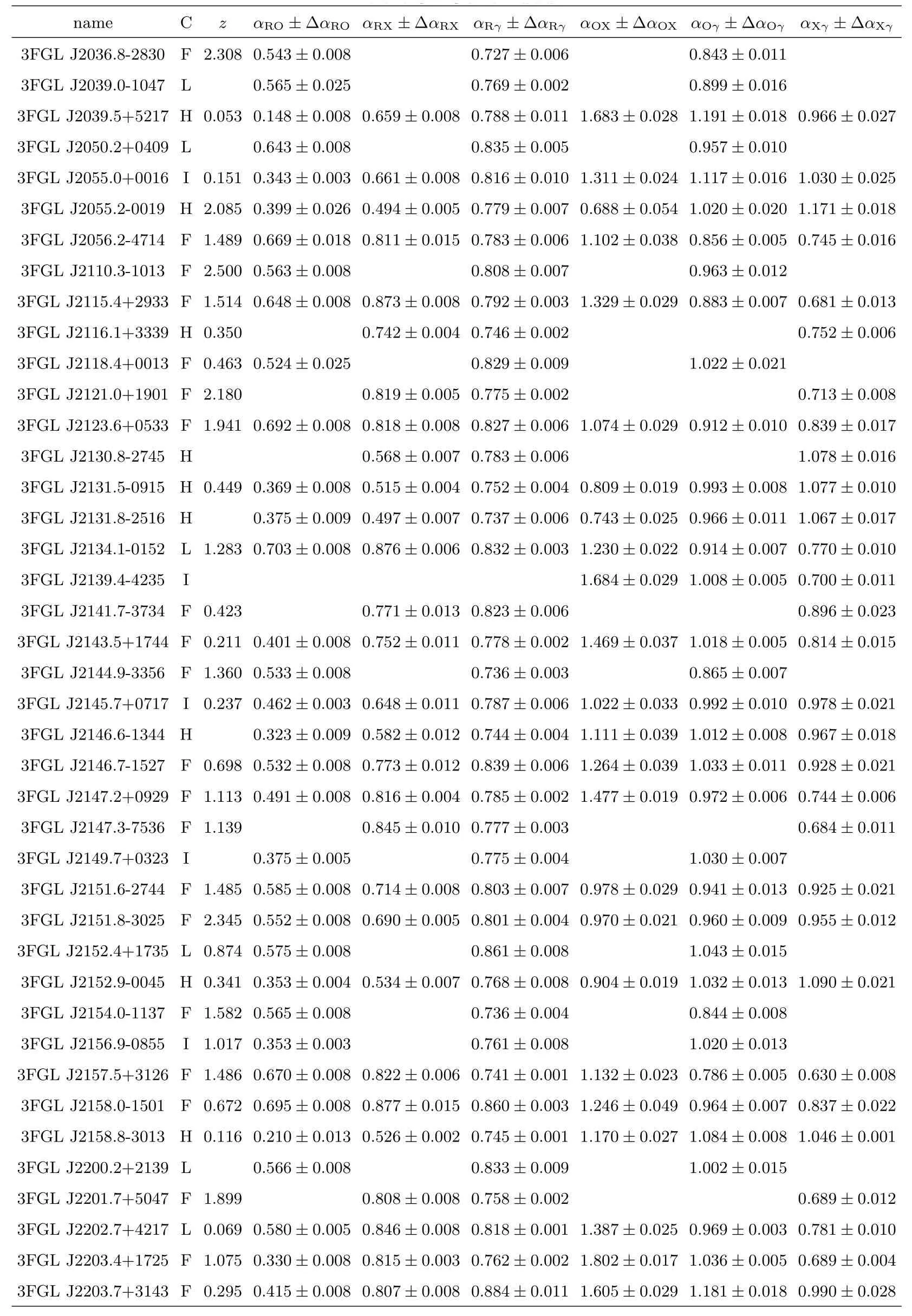
表3 续Table 3 Continued
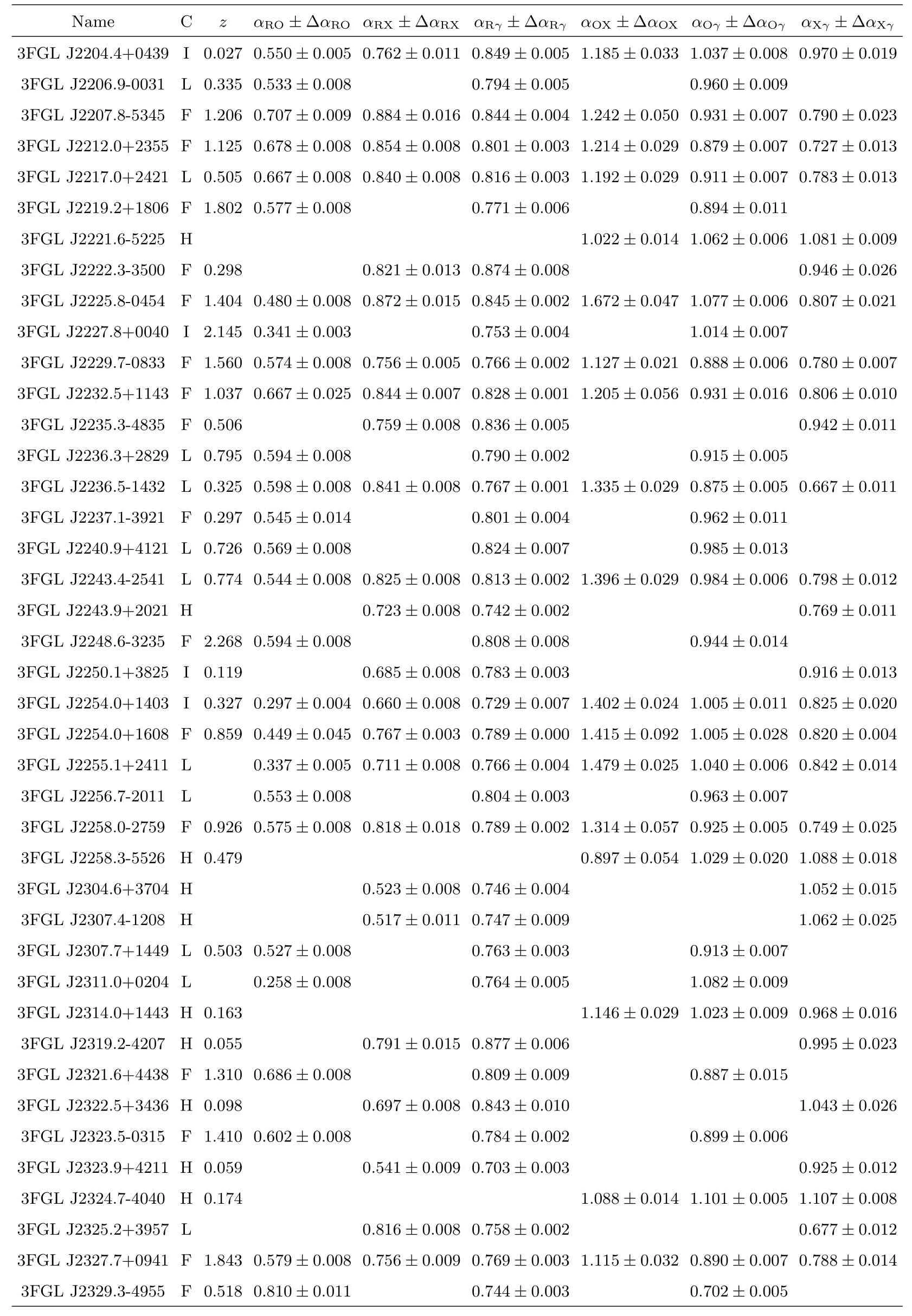
表3 续Table 3 Continued
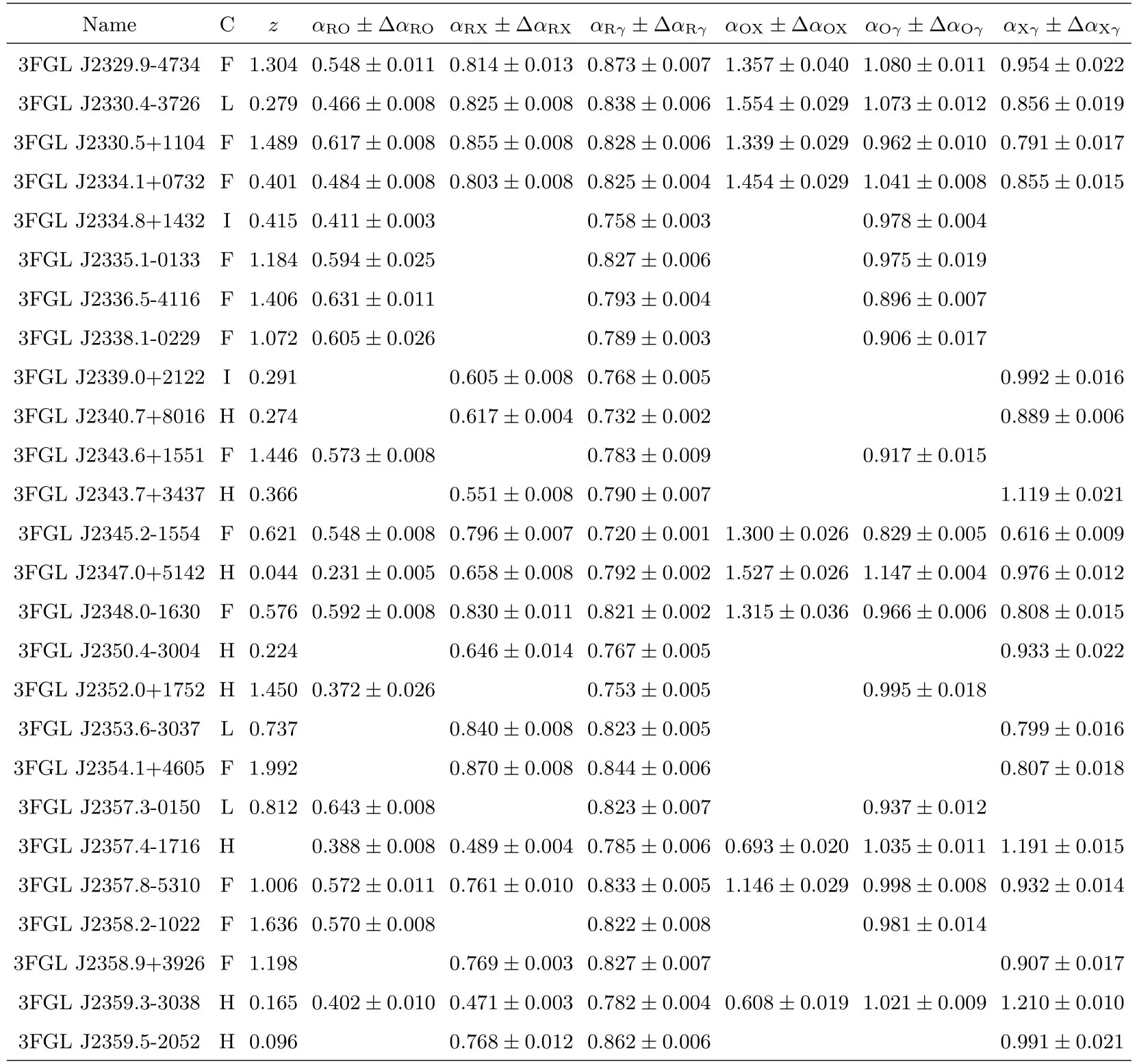
表3 续Table 3 Continued
