SOS:对称操作相似原理

2020-02-12翔编译自CheongSangWooknpjQuantumMaterials201953

物理学进展 2020年1期

李翔编译自Cheong Sang-Wook.npj Quantum Materials,2019,4:53

湖北师范大学先进材料研究院，黄石，435002

I.引子

自古以来，人类对自然界中许多事物所展现的对称性痴迷不已。早在公元前的西汉时代，《韩诗外传》就指出：“凡草木花多五出，雪花独六出”。这似乎是有史以来第一次思考雪花对称性之独特的记载。几千年来，人们在各种建筑物、文化符号（如太极图）、手工艺品及装饰图案等中引入了许多对称性概念，并且人体本身也包含着大量的对称元素和对称美的考量。不过，我们今天要讲的内容，却是要“打破”这种对称性。例如，在忽略一些细节时，左右手实际上是镜面对称的。假如不幸左手食指上出现一道难以恢复的巨大伤疤，此时，就称这一镜面对称性破缺了。或者，我们小心翼翼地除去雪花一角，它的六重旋转对称性也破缺了。虽然这种破缺可能是美学所忌讳的，但对称破缺阐释了生活及物理中最本质的意向：只有对称破缺的，才是丰富多彩的。当某件事、某件物过于对称和美丽时，可能破缺就要降临了。

事实上，所谓“对称性破缺”，可以简单理解为原来具有较高对称性的系统，由于出现不对称因素，其对称程度自发降低。这一概念在物理学中意义非凡。在过去的半个多世纪里，夸克、τ中微子以及希格斯玻色子的实验发现，称得上是科学史上的伟大成就。而洞见这些基本粒子存在的标准模型之实质与精髓，便是对局域SU(3)×SU(2)×U(1)规范对称性及其自发对称性破缺的分析。限于本文篇幅和译者水平，我们将不会、也没必要去讨论这一规范对称性。事实上，不仅仅是粒子物理，在凝聚态物理中，对称性及其破缺更是与众多的物理现象息息相关，诸如和相变相关的极化/磁化现象、强光照射下二次谐波发生、多种非互易二极管效应等等。

对称性及其破缺理论，在自然界中比比皆是，与各种物理现象如影随形。本文将不拘一格，从物理学中的对称性破缺出发，引出所谓对称操作相似(symmetry op erational similarity,SOS)原理，作为一柄“拙朴之剑”赠与各位醉心于凝聚态物理而不能自拔的学者，以期帮助读者深入理解各种复杂材料中的物理图像，乃至甄别新材料，抑或发现新奇的物理现象。愿读者循序渐进，细细品尝其中韵味。

我们知道，与晶体相关的重要对称性共有五类，即平移、旋转、镜面反映、空间反转和时间反演。不过，这些对称性之间并非完全独立。如空间反转，相当于在绕垂直轴进行180◦旋转操作之后，再进行一次关于水平面的镜面反映（即I=R⊕M，符号的定义将在下文给出)。这种不同对称性操作的等价性对本文论述十分重要，故提前提示于此。事实上，文献[1-9]对几乎所有晶体材料的对称性进行了详细的理论分析并加以分类。如若有兴趣，读者可自行前往查阅。不过需要指出的是，这些对称性分析通常极其复杂，并且只适用于一些特定的材料。有鉴于此，本文将避繁就简，只将讨论限定于若干具有代表性的系统（通常是一维体系）。这些系统简洁直观，却能够适用于众多不同的材料，并且与诸多可观测量或可观察的物理现象之间有很强关联。

II.非互易性与SOS原理

A.非互易性

想必大家对p-n结中的二极管效应非常熟悉。它最基本的功能就是对电流的“正向通过，反向阻断”。其实，二极管效应还有一个更“高大上”的名字—非互易性电荷输运。电荷输运容易理解，就是电子（或空穴）在电场下的流动。

非互易性在物理学中的解释是：对于一个对象，如果沿一个方向的运动行为与其沿反方向的运动行为有所不同，这一过程称为非互易方向二色性，或简称为非互易效应[7−9]1译者注：为了简化描述，后文将称这两种相反的运动行为是相互对立的，无论其互易与否。同时，由于这些运动行为通常由实验所观测，也可称之为不同的实验情况。。这里，所谓的对象，不仅可以是上述二极管效应中的电子，也可以是声子、自旋波、晶体中的光。

本文所要论述的是：这种非互易性，本质上由对称性及其操作决定。而如果能够从不同途径实现类似的对称性及其操作，则这些不同方案均可以产生相似的互易性效应。所以，本文的主题具有广泛的普适性和可实施性。

从对称性的角度来看，p-n结中之所以有这样的二极管效应，主要是其中的内电场E破坏了方向对称性[10]。研究发现，在一些铁电体（如BiFeO3）或极性半导体（如BiTeBr）中，极化P亦可以扮演着与内电场E相同的角色。因此，我们也能够在这些材料中观察到体二极管效应[11,12]。极化P之所以能够等效为内电场E，是因为二者均为极矢量(polar vector)，而极矢量在各种对称操作下会表现出完全一致的行为。

同理，磁场H和磁化M均为赝矢量(pseudovector)，故M亦可等效为H。2译者注：在物理学中，有极矢量和赝矢量之分。赝矢量可以表示为两个极矢量的外积。由于经常用于描述旋转，赝矢量也称轴矢量。极矢量与赝矢量在特定对称操作下有不同的行为：(1)在镜面反映下，极矢量垂直反映面（镜面）的分量反向、平行反映面的分量不变。相反，赝矢量垂直反映面的分量不变、平行反映面的分量反向。(2)在空间反转下，极矢量反向，赝矢量不变。这些特性在本文中至关重要。除了p-n结之外，诸如光隔离器、自旋电流二极管以及超材料(metamaterials)的许多原型器件都确实地利用了非互易效应。

另外，多铁性材料，作为原著作者和译者多年来的关注课题之一，也是实现非互易效应的优良候选体系。多铁性材料，通常指的是系统中同时存在铁电序和（反）铁磁序的化合物。其中，多种铁性之间相互依存、相互耦合。近年来，因其在磁电相互调控方面表现出的潜在可能性，多铁性材料受到世界范围的关注[13−15]。一方面，磁有序破坏了时间反演对称性；另一方面，当磁晶格与结构晶格相结合时（可以理解为自旋排列是空间不均匀的），将破坏系统的空间反转对称性。这一共同作用的结果最终导致多铁性的出现，也被称为磁致多铁。多铁性材料由于要求空间反转和时间反演两种对称性同时破缺，将会是下文中的“明星选手”。

B.SOS原理

首先，我们通过讨论速度矢量的对称性来进一步理解非互易性，并由此正式引入对称操作相似原理—SOS。

众所周知，速度矢量k（或线性动量，或波矢）表示为d x/d t（其中x为位移，t为时间）。这一矢量在空间反转(x→−x)或时间反演(t→−t)操作下将会改变其方向（即符号），故具备这两种对称性的破缺。注意到，k可以描述任意（准）粒子的运动，如电子、自旋波、声子和光子。在这里，基于简单起见，我们仅处理一维情形下的问题，以便将其中的物理阐述清楚明白。向高维的推广和演绎直截了当，虽然较为繁琐。兹作如下符号约定，用于表示相应的对称操作：

R，绕垂直于k矢量的轴旋转180◦；

R，绕沿k矢量的轴旋转180◦；

I，空间反转；

M，以垂直于k矢量的平面作镜面反映；

T，时间反演。

根据以上符号约定，显而易见，+k在R对称操作下将变为−k，即k具备破缺的R对称性。事实上，+k在I、M或T中任何一个对称操作下均变为−k，因此，{R,I,M,T}便称为k的所有对称性破缺操作的集合。这一表达在本文中屡屡现身、至关重要。

那么，如何理解其中的非互易性呢？首先引入一个概念，构成量(specimen constituent)。可以把构成量理解为材料或系统中的一种物理环境，如电子在电/磁场中运动时，这个电/磁场环境即是一种构成量。光在晶体中传播时，能够与光发生相互作用的晶格结构也是一种构成量。

简单而言，如果用一个代表状态的矢量A来描述这个构成量，那么系统就可以用[+k,A]来表示。如果用另一个状态矢量B来描述经过对称操作后的构成量，那么经过变化后的系统就是[−k,B]。因此，若要讨论其中的互易性，只需要知道在通过对称操作使[+k,A]变为[−k,B]的过程中，构成量是否发生了变化。

从上面的分析可知，若想把+k变为−k，必然要进行{R,I,M,T}对称操作。此时，如果构成量不发生变化（即A=B），那么由于+k和−k所处的物理环境（构成量）相同，运动行为将不会发生改变，实验结果是互易的。这里，将这一过程表述为对称操作前后是可以关联的，即[+k,A]在{R,I,M,T}对称操作（只要有一个对称操作即可）之后变成了[−k,A]。

反之，若构成量发生变化(A ̸= B)，即{R,I,M,T}中的任意一个对称操作均无法关联[+k,A]和[−k,B]，则由于+k和−k所处的物理环境（构成量）不同，运动行为必将改变，也就是会展现出非互易性。换言之，如果构成量也是{R,I,M,T}对称性破缺的，那么B和A必将不相等，即实验结果一定是非互易的。

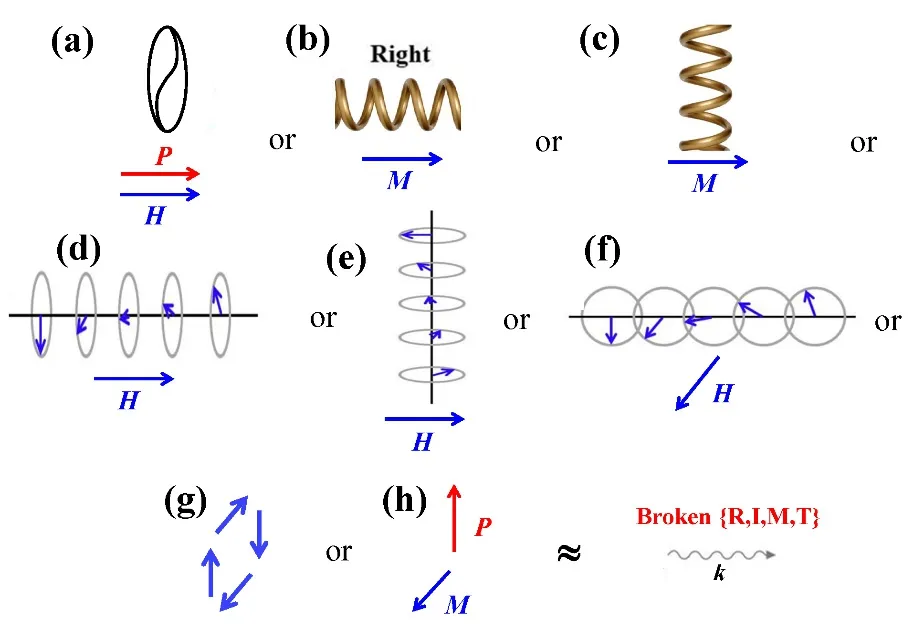
图1.具有针对k的SOS之多种构成量。其中，红色箭头表示极化P或者外电场E，蓝色箭头表示磁化M或外磁场H。(a)铁转(ferro-rotation)a。(b)&(c)具有磁性M的结构手性（螺旋型）。(d)&(e)磁场H下的螺旋(helical)自旋序。(f)磁场H下的面内螺旋（cycloidal，或称摆线）自旋序。(g)由自旋旋转构成的环磁极矩(toroidal moment)。(h)由P和M（或E和H）构成的环极矩(toroidal moment)b

因缺乏更好的术语表述，我们姑且把这些具备{R,I,M,T}对称性破缺的构成量，称为具有针对k的SOS(symmetry operational similarity)。

很显然，SOS并非只是针对互易性这一物理，如上所述只是局限于非互易性有关的SOS原理而已。

图1列出的所有构成量，均具有针对k的SOS（即它们与k具备对称操作相似性，在图1中用“≈”表示)。根据SOS原理，它们均能展现出非互易效应。另外，在图1中，我们只考虑了k的一维特性，因而可以忽略沿一维方向的平移对称性。同时，也可忽略图1(e)所示构成量的对称性。

这里，建议读者将本文所有图中构成量的对称破缺性质“演练”一遍。事实上，唯一张纸、一支笔、一双手和一个富有空间想象力的大脑足矣。译者在一些不易想通的地方作了提示，希望有所帮助。在分析对称性时，可以简单地参考手性变换、极矢量与赝矢量的对称变换特性。虽则简朴，其效无量！

例如，在结构手性材料中，当沿手性轴施加磁场时，沿手性轴方向传播的自旋波或光波将展现出非互易效应，即所谓的磁—手性效应，对应于图1(b)。实验上，在立方手性结构Cu2OSeO3中已经观察到非互易的磁—手性自旋波效应[16]。另外，理论计算预测，在单轴手性Ba3NbFe3Si2O14也存在类似的磁—手性效应，并且得到实验观测证实[17,18]。当手性轴与磁场垂直时，非互易效应依然存在，此即横向磁—手性效应，对应于图1(c)3译者注：结构手性具备对称性破缺，如右手手征在{I,M}操作下将变为左手手征。赝矢量M（或H）具备对称性破缺，故结构手性和磁性共同作用将具备{R,I,M,T}对称性破缺。。

另一个非互易自旋波的例子是磁场沿螺旋轴方向的螺旋自旋构型（或锥形自旋构型），对应于图1(d)。这一现象在铒金属中被观察到[7]4译者注：自旋螺旋构型和结构手性具备SOS，即二者均破坏了对称性。这里，为了更方便理解螺旋自旋序的对称性，在讨论其对称操作时，读者只需要关注自旋序旋转方向的对称性，无需考虑每一个自旋。。

图1(h)描述了一种环极矩的情形。在极性磁体FeZnMo3O8中观测到的非互易THz光学效应，即属于这一情形。其中，P沿c轴，H（或M）处于ab面，传播光沿着垂直于P和H（或M）的第三个方向[20,21]。另外，图1(a)描绘了一种具备P和M（或在电场E和磁场H中）的铁性—旋转。文献[15]详细地讨论了其中的结构手性和铁转特征，在此不再赘述。

注意到，上面所讨论的对称性考虑，或多或少地也适用于一些准平衡过程，如电子输运实验。其中，k表示电子云的漂移速度，与电流矢量J直接相关。不过，我们需要施加一外电场才能得到相应的k或J。由于{R,I,M}对称操作能够将图2所示的左右两种实验情况联系起来，因此，那些具有{R,I,M}破缺对称性的电极化（或电场）构成量，以及图2所示的具有{R,I,M}+{T}破缺对称性的非互易情形，将都能展现出非互易电子输运特性。

图2.准平衡过程中电子输运的非互易效应。其中，左右两种相互对立的实验情况可以通过{R,I,M}对称操作关联

以上描述也可以作如下概括：

在准平衡过程中，如果相互关联的两种运动行为（实验状态）可以通过某一对称操作集合而联系起来，则当某一构成量在该对称操作集合下发生破缺时，这两种实验状态下所观测到的该构成量将是非互易的。

这是与非互易性有关的SOS原理之另一种表述方式。事实上，通常p-n结和铁电BiFeO3中所展示的二极管效应，正是这里所提到的非互易电子输运特性[10,11]。手性碳纳米管中的磁电阻也可以是非互易的，对应于上文图1(b)中所提到的磁—手性效应[21]。在BiTeBr材料中，当在ab面内施加一磁场H、并且极化P沿c轴方向时，沿第三方向（垂直于P和H）的电导率将是非互易的，即同样会表现出如图1(h)所示的非互易环极矩效应[12]。

III.多铁与线性磁电材料

A.针对极化与磁化的SOS

多铁性，尤其是磁致多铁性，也可以用针对极化P的SOS来理解[22]。在这里，和T”将是针对P方向而定义的对称操作，不再是前文中针对k的对称操作。类似地，{R,I,M}便称为P的所有对称性破缺操作的集合。我们把所有（准）一维下具备{R,I,M}破缺的构成量示于图3(a)∼(d)中。它们都具有针对P的SOS。同样地，沿一维方向的平移对称性和如图3(a)所示的对称性也可忽略。

需要强调一点：众所周知，极化P在T操作下并不存在对称性破缺，故针对极化P的SOS中并不要求T对称性破缺。

接下来，我们举一些实例，以便更好理解：

1.在TbMnO3和LiCu2O2体系中，多铁性来源于（面内）螺旋自旋序(cycloidal spin order)，对应于图3(a)[23,24]。

2.在RbFe(MoO4)2和CaMn7O12体系中，多铁性来源于铁转(ferro-rotational)形式的螺旋自旋有序(helical spin order)，对应于图3(b)[25,26]。

3.在Ca3CoMnO6、TbMn2O5和正交HoMnO3中，多铁性来源于两个或两个以上不同磁性位置（离子）的交互作用，对应于图3(c)[27−29]。

4.在Ba2CoGe2O7中，多铁性来源于所谓的p-d轨道杂化作用，对应于图3(d)[30]。

接着，我们来看图3(e)和(f)所示的构成量：当外磁场H=0时，在{R,I,M}破缺集合中，构成量仅分别对{I,M}和{R,I}操作发生对称性破缺。当H非零时，才会发生{R,I,M}的对称性破缺，即具有针对P的SOS，如Cr2O3等材料中的线性磁电耦合效应。图3(e)所示的情形对应于低磁场下对角的线性磁电耦合，图3(f)所示的情形则对应于磁场H高于自旋翻转临界场下非对角的线性磁电耦合[31]。如果在图3(e)和(f)中将磁场H反向（比如通过R或M操作），相应地P将发生翻转。这与线性磁电耦合的基本物理性质相吻合。

最后，再来讨论磁化M。{R,M,T}是M的所有对称性破缺操作的集合。当图3(e)和(f)中施加的外场不再是磁场H而是电场E时，它们将发生的对称性破缺，即具有针对M的SOS，出现磁性。这反映了线性磁电耦合材料（如Cr2O3）中电场诱导磁化和磁场诱导极化之间的相互关系。事实上，我们也注意到，当把H替换为梯度应变矢量（即应变是非均匀的）时，它同样具有针对M的SOS—也就是说，所有的线性磁电材料均能在梯度应变的作用下出现净磁矩，即所谓的挠曲磁性(flexomagnetism)。另外，在后文的图4(b)∼(f)中，倘若把H替换为梯度应变矢量，亦将展现出挠曲磁性。

接下来，可以考虑一件非常有趣的事：如果在材料中通过某些非平凡的手段，使得相应的对称性发生破缺，那么根据SOS原理，是否就能获得一些新奇的物理现象呢？

答案是肯定的。现以图3(g)所示的构成量为例。当在具有螺旋型的结构手性晶体中注入电流时，相当于人为地引入了电流矢量J。根据对称操作原则，J具备破缺的{R,T}，而结构手性具备破缺的，二者结合将使得该构成量发生{R,T}对称性破缺，即出现针对M的SOS。这正是在非磁性材料中引入磁性的重要方法，并且已经在结构手性的碲晶体中观察到了线性诱导出的M[32,33]。另外，在图3(h)中，当Neel型铁电畴壁在垂直于壁的方向上移动时，同样应当具有磁性[34]。不过这种情况尚未通过实验证实，但参考文献[35]中关于动态多铁性的讨论即是关于这一问题。

B.预测未知的磁电效应

对预测磁致铁电和线性磁电耦合新材料，上文提出的SOS原理，将会是非常有力的工具。例如，在图4(a)中，同时存在两种磁性离子（AAB型）的离子有序和上—上—上—下—下—下(↑↑↑↓↓↓)型磁有序。它们具有针对P的SOS，因此应当表现出磁致铁电性。再如，图4(b)中，前两种用于表示磁单极子5译者注：此处的磁单极子并非是理论物理学中假设的基本粒子，而是存在于某些凝聚态物质系统中非孤立的磁单极准粒子，如自旋冰(spin ice)。，第三个用于表示环磁极矩，第四个用于表示磁四极子。它们在零磁场下并不具有针对P的SOS6译者注：前两个不具备{R}破缺，后两个不具备{M}破缺。，不过却会在磁场H下出现针对P的SOS，故能表现出线性磁电耦合效应。图4(c)∼(f)所示的（翘曲）蜂窝晶格自旋构型也非常类似，仅当施加了非零磁场H时，它们才会具有针对P的SOS，从而表现出线性磁电耦合效应。

需要指出的是，上述多数构成量尚未得以有具体实验证实。不过，若未来能够在实际材料中对这些源自对称性的预测加以验证，那必将是极具意义的[36]。

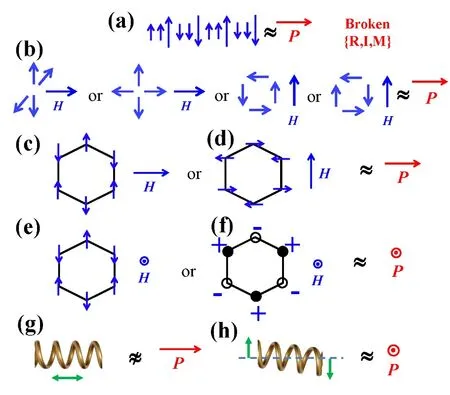
图4.具有针对P的SOS的构成量。红色箭头表示P，蓝色箭头表示自旋或M。(a)AAB型离子有序结合上–上–上–下–下–下型自旋有序。(b)与H垂直的磁单极子，与H共面的磁单级子，与H共面的环磁极矩，与H共面的磁四极子。(c)∼(e)磁场H下蜂窝晶格中不同的面内反铁磁有序构型。(f)翘曲蜂窝晶格中的伊辛反铁磁有序a，其中，磁场垂直纸面向外，实心圆表示处于纸面之下的自旋，空心圆表示处于纸面之上的自旋，“+,−”符号分别表示自旋垂直纸面向外或向内。需要指出的是，当(f)中磁场H的方向变为纸面内水平向右时，相应的构成量将具有针对“纸面内水平向右的P”的SOS。(g)处于均匀应力下的螺旋型手性结构，其中绿色双箭头表示均匀应力场。(h)处于剪切应力（纸面内）下的螺旋型手性结构，绿色箭头表示剪切应力

我们举一个相关的例子来佐证：六角晶系的R(Mn,Fe)O3（R为稀土离子）。

这一体系属于反常(improper)铁电体，它在ab面内存在自发的Mn/Fe三聚体(trimerization)，铁电极化沿c轴方向。已经在六角R(Mn,Fe)O3体系中发现了多种面内Mn自旋的磁有序。其中，Mn三聚体与所谓的A1型磁有序共同作用，能够诱导出净环磁极矩。而所谓的A2型磁有序可以为系统引入磁单极子[37,38]。线性磁电耦合效应以及与这些磁单极子、环磁极矩相关的非互易性，将会是未来研究的主题。

IV.压电效应

一般来讲，压电效应存在于非中心对称的晶格结构中。然而，3行6列的压电张量处理起来非常复杂，并且即使在非中心对称系统中，有些压电系数也有可能是零。我们知道，在32种晶体点群中，有11种是中心对称的，不具有压电性；同时，属于点群432的晶体虽无对称中心，但其对称性较高，也没有压电性，压电晶体只可能属于20个非中心对称的点群[1,2]。接下来，我们将利用SOS原理从对称性的角度来理解压电性的起源。

所谓压电，指的是晶体在受到应力作用时能够在某些表面上产生电荷，也就是诱导出P。因此，在考虑压电的构成量时，有两个要素：一是应力场（均匀应力或者剪切应力），二是能否具备针对P的SOS。例如，在图4(g)的螺旋手性结构中，沿任意主方向上的均匀应力都无法使这个构成量具备针对P的SOS，因此压电系数dij(i,j=1,2,3)=0。也就是说，均匀应力无法带来压电性。

然而，当这一螺旋手性结构中存在如图4(h)所示的剪切应力时，由于螺旋手性结构本身具备{I,M}对称性破缺，而引入的应力场具备{R}对称性破缺，这一构成量将具备针对P的SOS，即d14、d25和d36非零，因此具有压电性7译者注：当手性材料施加了如图所示纸面内的剪切应力后，除了垂直于纸面方向的二次旋转轴外，其它方向的旋转对称性全部消失。根据二次轴的对称性要求，材料中的电偶极矩只可能沿着该二次轴方向，故P只能垂直于纸面，即d14非零，d24=d34=0。同理，d25和d36非零，d15=d35=d16=d26=0。。事实上，图4(g)&(h)所描绘的情景，正对应着点群2122和222中的压电性。

V.角动量与非互易

前文讨论非互易性时，尚未涉及过角动量。本小节将展示，考虑角动量后，SOS原理依然有效。例如，圆偏振光具有自旋角动量，绕传播轴螺旋状扭转的涡旋光束或电子，就具有了轨道角动量[39−42]。当具有角动量l的物体沿着一个方向以波矢k运动时，可以通过{R,T}对称操作，把它关联到与其相互反向的运动上，如图5(a)所示。这里，根据SOS原理，只要构成量不破坏{R,T}对称性，那么它将是互易的。例如，当一个具有角动量的对象，沿着手性材料的手性轴方向运动时，由于手性结构不破坏{R,T}对称性，所以是互易的。最典型的例子就是手性材料中的互易旋光性；沿着手性轴向两个相反方向传播的线性偏振光，有着完全相同的偏振旋转。

然而，当材料中的{R,T}对称性发生破缺时，情况将变得很不同。我们知道，M会打破{R,对称性。如此一来，构成量中的M如果介入含有角动量的运动，就会导致非互易效应。例如，沿着磁化轴方向传播、且具有角动量的运动对象便是非互易的，事实上，这种非互易性正是铁磁或亚铁磁材料中出现法拉第旋转的根源，也直接与磁光克尔效应(magnetooptic Kerr effects,MOKEs)有关，后文会再次回到这一问题上来。

在对亚铁磁石榴石Tb3Fe5O12进行THz涡旋束传播实验时，首次发现了具有轨道角动量的涡旋光束存在非互易性[43]。类似地，环磁极矩也具备破缺的{R,T}，因此，当传播方向沿着材料环磁极矩的方向时，具有轨道角动量的涡旋光束和圆偏振光也将展现出非互易效应。此外，结合了电场E或极化P的磁单极子，在有角动量存在的情况下也将具备{R,T}对称性破缺，从而展现出非互易效应。

以上讨论的所有情形都可以总结在图5(a)中，不过，其中大部分还有待实验证实。也就是说，这些实验将是创新性的、值得实施的。

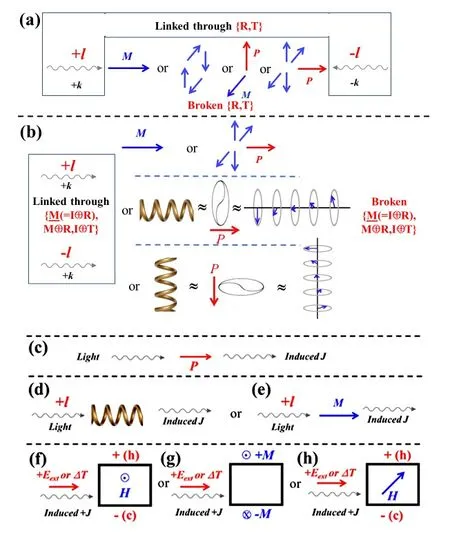
图5.与角动量相关的多种物理现象，这些角动量可以是圆偏振光中的自旋角动量，也可以是涡旋电子或光束中的轨道角动量。(a)引入角动量后的非互易效应。其中，左侧和右侧可以通过{R,T}对称操作关联。对于其中给出的构成量，蓝色箭头表示自旋或M，红色箭头表示P，它们均具备{R,T}对称性破缺。(b)=I⊕R),M⊕R,I⊕T}对称操作可以将具有相反角动量的运动行为关联起来。右侧所示的所有构成量均具备破缺的M⊕R,I⊕T}，故对角动量符号有依赖性。(c)一种准平衡过程，表示外电场下p-n结中的诱导电流，或者光照下极性材料中的诱导电流，这对应着p-n结和铁电体中的光伏效应；(d)&(e)手性材料或铁磁材料在圆偏振光或涡旋光束(l)照射(k)下能够诱发光电流，即圆偏振光致电流效应。(f)∼(h)不同类型的霍尔效应，其中，E ext是外场，∆T是温度差，“+,−”代表诱导的霍尔电压，“h:hot,c:cold”代表诱导的霍尔热梯度。图(h)中的H与J成45◦

需要说明的是，不破坏空间反转对称的铁转(ferro-rotation)本身并不具有旋光性8译者注：因为电偶极子构成的铁转结构与时间无关，具备T对称；同时铁转具备I对称，故不会破坏{I⊕T}对称性。；但是，当施加外电场E时，铁转将同时具备破缺的I⊕R),M⊕R,I⊕T}，最终引发互易旋光性。这种互易旋光性正比于外电场，被称为线性电致旋光[45]。

VI.SOS之拓展：准静态电子输运

本文一开始即阐释清楚，铁电体中的P可以等效于p-n结中的内电场，能够带来非互易电子输运特性。因此，在光照下，于p-n结中常见的光伏效应也能在铁电体中表现出来[10,11]。事实上，光伏效应反映的是一个系统在持续光照后的准平衡过程，因此，持续光照这一过程本身就破坏了时间反演T对称性。所以，后续的准平衡过程不必再去额外考虑T，这一点类似于外电场下的电子输运。这里，可以从另外一个对称性的角度来看待这些准平衡过程，并延伸出一个新的概念—对称操作系统性(symmetry operational systematics)。它表明构成量中的某一物理现象在所有对称操作下（除T）都能够系统地、有规律地变化。

其实，对称操作系统性跟对称操作相似原理的理念类似，可以作为SOS的延伸。并且巧合的是，它的首字母也是“SOS”，姑且称这位孪生兄弟为SOS#。比如图5(c)所示的构成量中，P和J在所有对称操作下（除T）或保持不变，或同时改变方向。这就是一种SOS#。

来看一个简单的例子：已知手性材料在圆偏振光(l)照射(k)下能够诱发光电流，被称为圆偏振光致电流效应(circular photogalvanic effects,CPGE)[46−48]，如图5(d)所示。现在，我们用SOS#来探讨其中的对称性要求。若要产生这一光致电流效应，其对称性的要求是：在诱导电流J保持不变的前提下，对称操作必须能够使偏振(l)和手性同时改变方向，如或M⊕R。根据SOS#，若把手性材料换成图5(e)所示的铁磁/亚铁磁材料（或者施加了外磁场的任意材料），它在或M⊕R对称操作下，偏振(l)和磁性(M)也会同时反向，将同样能够展现出CPGE。不过，到目前为止，似乎尚未讨论和实验证实过铁磁/亚铁磁材料中的CPGE。

相信读者对霍尔效应耳熟能详，以上所述的SOS#，正可以应用来描述所有类型的霍尔效应输运行为[49−55]。图5(f)所示的四种组合(Eext,+,−),(Eext,h,c),(∆T,+,−)和(∆T,h,c)分别对应着霍尔效应、爱廷豪森(Ettingshausen)效应、能斯特(Nernst)效应以及热(Thermal)霍尔效应，其中，Eext是外场，∆T是温度差，“+,−”代表诱导的霍尔电压，“h:hot,c:cold”代表诱导的霍尔热梯度9译者注：简单说明一下，由于磁场的存在，霍尔效应描述的是垂直于电场方向上出现的电势差。爱廷豪森效应描述的就是温度差；能斯特和热霍尔效应只是把电场E ext变为温差∆T而已。。在图5(g)中，Eext对应着自旋霍尔效应，∆T对应着自旋能斯特效应。图5(h)所示的四种组合(Eext,+,−),(Eext,h,c),(∆T,+,−)和(∆T,h,c)分别对应着平面霍尔效应、平面爱廷豪森效应、平面能斯特效应以及平面热霍尔效应。

在以上这些构成量，线性霍尔效应均能根据对称操作（除T）系统地、有规律地变化，即展现出SOS#。以图5(h)为例：在实验上，当H（在纸面内）旋转90◦时，诱导的平面霍尔电压(+,−)或者热梯度(h,c)将会发生180◦翻转；而从对称性上，I⊕R)操作刚好能够同时使得H旋转90◦以及电压/热梯度翻转180◦。当然，这是在H和J（Eext与J同向）的夹角φ为45◦时的特例。事实上，当φ为任意角度时(0<φ<90◦)，平面霍尔电压(+,−)或者热梯度(h,c)将线性正比于sin 2φ，为非零值。当图5(f)和(h)中的H被M替代时，相关的效应将是“反常的”，比如在图5(f)中(Eext,+,−)+M的组合即为反常霍尔效应。

如果在图5(f)∼(g)中的构成量增加某一具备破缺对称性的元素集合时，将会诱发非线性效应。下面以图5(f)中的霍尔效应(Eext,+,−)+H为例加以说明：

另一方面，{R•,I}中的任意一个对称操作均能使得J和(+,−)同时反向且保持H不变。此时，当构成量中出现破缺的{R•,I}时，诱导的霍尔电压(+,−)与J的关系将由线性转变为非线性。事实上，手征的极性材料（手性轴和极化轴均垂直于纸面）就具备破缺的M|⊕R•}但不具备破缺的{R•,I}，根据SOS#，诱导的霍尔电压(+,−)与H的关系变为非线性，但是与J的关系保持线性。

VII.MOKE型旋光

SOS原理也可以用于分析正入射线偏振光的反射光束是否会偏振旋转。图6中左上和右上所示的两种实验情况，可以通过⊕R,T}对称操作关联起来，并且下方所示的构成量均具备破缺的M⊕R,T}，因此可以展现出偏振旋转性质。其中，图6(a)用于表示铁磁体中反射光的偏振旋转，这对应于标准的MOKE；图6(b)对应着无净磁矩的反铁磁Cr2O3中反射光的偏振旋转[56,57]；图6(c)对应于磁单级子中反射光的偏振旋转；图6(d)是图4(c)中所述的具有面内伊辛反铁磁有序的蜂窝晶格；图6(e)是图4(f)中所述的具有面外伊辛反铁磁有序的翘曲蜂窝晶格。需要注意的是，这里光束应当是垂直于蜂窝晶格面的，图中用一个90◦翻转箭头标出。图6(f)的kagome晶格与MOKE型旋光性有关，这一旋光性在具有极小净磁矩的反铁磁Mn3Sn中被观测到[58]。需要指出的是，如果图6(f)中的偏振光垂直于kagome晶格入射，将不会出现MOKE型旋光，因为存在一个未破缺的对称性，它的镜面由纸面内的垂直轴和纸面的法向共同确定。

遗憾的是，磁单极子和上述（翘曲）蜂窝晶格中的MOKE型旋光尚未得到实验证实。不过可以预测，磁单极子效应极有可能在六角R(Fe,Mn)O3的A2相中实现。同时，要想在具有伊辛反铁磁有序的（翘曲）蜂窝系统中观察到MOKE型旋光的宏观体效应，则要求多层蜂窝晶格的贡献互不抵消。

VIII.二次谐波发生(SHG)

非线性光学主要涉及到光学上的相干过程，其中光与物质的相互作用能够改变光的频率。最简单的例子就是具有倍频的二次谐波发生(second harmonic generation,SHG)。这种效应通常是相当弱的，想要观察到的话，必须提供很高的电磁场强度，如采用大功率脉冲激光。由于晶体化合物的点群对称性以及磁对称性对SHG的产生有着决定性的作用，因此可以利用SHG来观察铁磁或反铁磁畴等。下面用SOS原理来讨论哪些材料能够产生SHG。

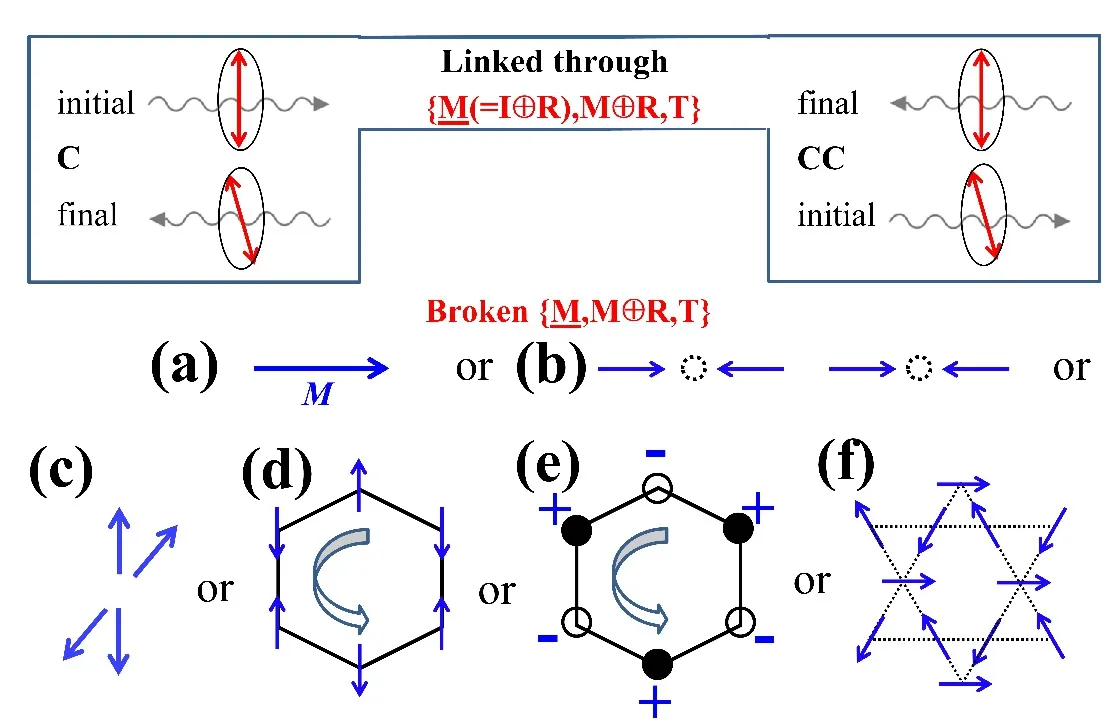
图6.线偏振光反射光束的偏振旋转。红色双箭头表示偏振方向，蓝色箭头表示自旋、磁化或极化。左上和左下两种情形可以通过,M⊕R,T}对称操作关联，而(a)∼(f)列举的所有构成量均具备破缺的⊕R,T}，因此能够展现出光的偏振旋转（MOKE型旋光）。需要指出，偏振光都是从左向右传播。特别地，为了方便示意，(d)和(e)中两个(翘曲)蜂窝状构成量实际上沿着纸面内的竖直轴旋转了90◦（已在图中标示），即光应当是垂直于蜂窝面传播的。

对于正入射的相干光，如果反射光束的偏振态与入射光束平行，就可以用一种较为简单的对称性方法来分析：用SHG(X X)表示，其中前后两个X分别代表入射和反射光的偏振方向。图7(a)中左侧和右侧所示的实验情况可以通过(=I⊕R|)}对称操作关联。因此，如果某一材料具备对称性中的任一种，那么它对X方向偏振入射光的光学响应将不具有非对称分量，即出射光的正负偏振完全抵消，无法观察到SHG(X X)。相反，如果任何材料具备破缺的那么SHG(X X)就会出现。

图7(c)∼(f)给出了多种（翘曲）蜂窝晶格中的反铁磁构型，其中的二重旋转轴垂直于纸面。一方面，在不考虑反铁磁序的情况下，只有翘曲蜂窝晶格才具备破缺的另外，如果以水平的、并且垂直于翘曲蜂窝晶格面的镜面作为反映面，对称性也将破缺。也就是说，如果X方向垂直于纸面，图7(d)和(f)所示的翘曲蜂窝晶格将会展现出SHG(X X)。比如当X垂直于非中心对称的GaAs之(111)面时，就是这种情况。另一方面，如果考虑反铁磁序，图7(c)∼(f)中的所有构型均具备破缺的同时，如果以图中绿色虚线作为镜面（镜面垂直于纸面），它们也将具备破缺的此时，如果X方向垂直于纸面，那么SHG(X X)将会发生。比如在Cr2O3中就利用这种磁SHG(XX)观察到了反铁磁畴[59]11译者注：需要注意的是，虽然反铁磁畴有着不同的SHG相位响应，但通常SHG的强度是通过实验测量的。由于畴壁的强烈干扰，图像中只有畴壁能够表现出对比度。不过，当磁SHG与晶格SHG结合时，由于二者叠加时涉及到磁SHG的正负号，将能够表现出对比度[59]。。

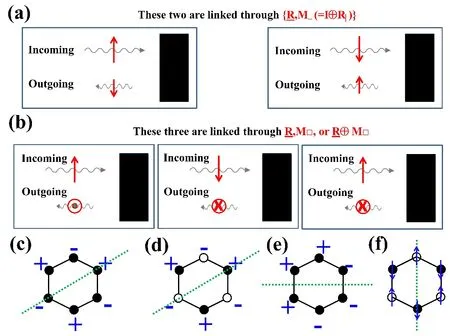
图7.正入射相干光的SHG的对称性分析。(a)正入射的相干光，反射光束的偏振态与入射光束平行，对应于SHG(X X)。左侧和右侧两种情形可以通过对称操作关联，当构成量发生对称性破缺时，将出现SHG(X X)。红色箭头表示相干光中的电场（或极化）；(b)能够关联第一、二两种构成量，（☐代表纸面）能够关联第一、三两种构成量。当材料具备破缺的，SHG(X Y)就会出现；(c)&(e)蜂窝晶格中的面外反铁磁构型；(d)&(f)（翘曲）蜂窝晶格中的反铁磁构型，其中，实心圆表示处于纸面之下的自旋，空心圆表示处于纸面之上的自旋。注意，在(c)∼(f)中，相干光应垂直于纸面入射。它们均具备破缺的对称性，也具备破缺的（绿色虚线代表镜面，镜面与纸面垂直）或对称性。可利用SHG(X X)或SHG(X Y)观察其中的反铁磁畴。

现在我们将正入射相干光的SHG效应进行如下概括：

2.当X垂直于Mn时，将发生SHG(X X)效应；当X平行于Mn时，将发生SHG(X Y)效应（Y垂直于Mn）。

这里的第(2)条前面已经讨论过。对于第(1)条，我们可以使用如下反证法：

假设不存在破缺的Mn(=I⊕Rn)对称性，那么我们可以找出两个不破缺的、相互垂直的镜面反映Mn1和Mn2。此时，Mn1⊕Mn2=(I⊕R1)⊕(I⊕R2)=R1⊕R2，其中，R1和R2的旋转轴分别垂直于Mn1和Mn2。由于Mn1和Mn2是任意的，我们完全可以选择这样两个镜面，使得R,R1和R2相互垂直。如此，我们有R1⊕R2⊕R =1。因为二次旋转轴所以Mn1⊕Mn2=R1⊕R2=由于Mn1和Mn2不破缺，故不破缺，与条件相悖。证毕。

IX.总结与展望

行文至此，相信读者或多或少对SOS原理有了一定的了解。本文中，我们详细探讨了诸如非互易性、磁致铁电、线性磁电效应、旋光性（包括磁光克尔旋转和法拉第旋转）、光伏效应以及二次谐波发生等物理现象，并且有理由相信SOS原理可以作为有力的手段，去甄别那些具有潜在新效应的材料。不过，在以上的讨论中，很有可能遗漏了一些能够展现出特定物理现象的未知构成量。当然，如果要在实际材料中实现本文所描述的各种效应，不同一维链或二维层之间的贡献必须能够合理而有效地叠加成宏观效应。

好吧，现在我们可以总结一下SOS原理能够给出的各种新奇预测，包括：

1.磁螺旋序具备针对结构手性的SOS，将能展现出旋光性；

2.在图1(c)单轴手性材料中，将能出现光学传输或电子输运的横向磁—手性效应；

3.对图1(g)中由旋转自旋构成的环磁极矩，能够观察到非偏振光或自旋波传播的非互易性；

4.当Neel型铁电畴壁沿着垂直于畴壁的方向运动时，能够诱导出垂直于极化旋转方向的磁性；

5.图4以及图5(a)&5(b)中很多未在实际材料中观察到或考虑过的现象；

6.图5(c)中未在实际材料中观察到或考虑过的铁磁/亚铁磁CPGE效应；

7.图5(f)中未在实际材料中观察到或考虑过的非线性霍尔型输运性质。这些性质从技术来看，应该比较容易在实验中得到检验；

8.图6中磁单极子系统和具有反铁磁伊辛序的（翘曲）蜂窝系统中，可能存在MOKE型旋光性；

9.利用SHG成像技术观察图7(c)&7(e)&7(f)中的反铁磁（翘曲）蜂窝晶格系统。

令人欣慰的是，利用SOS原理进行预测之后，横向磁手性效应已经成功地在Ni3TeO6中观测到[60]。

最后，需要指出，在测量方面，笔者根据SOS原理揭示了正入射相干光的SHG准则见（SHG部分）。该准则不仅适用于晶格结构，也适用于磁结构。进一步，在测量方面亟需进行的一项富有挑战性的工作是：利用诸如非互易性或光学偏振旋转等特性，对反铁磁（包括磁单极子和环磁极矩）畴/畴壁或铁转畴/畴壁进行空间分辨(<1 mm)成像。具有轨道角动量的涡旋光或电子束，也将是用来探测与对称性破缺相关联物理现象的强力手段。

X.后话

最后，略显遗憾的是，SOS原理既不能说明物理现象的微观机制，也不能预估它们的大小。不过，正如在图3(a)中所展示的那样，所有具有螺旋自旋序的磁体在实验中均展现了可观测的极化P。我们坚信，如果某一物理现象在对称性破缺考虑下是允许的，那么这个效应通常就足够大到可以被实验所观测。这似乎与著名的Murray Gell-Mann论述遥相呼应：“everything not forbidden is compulsory（只要没有基本原理禁止它发生，它就可以发生）”[61]。