基于高精度测量仪的2K-V型减速器虚拟样机的建立

韩林山， 焦文华， 曹宸旭

（华北水利水电大学 机械学院，郑州450000）

0 引 言

随着国家工业的发展，21世纪以来中国的工业水平迅速得到了提高，并提出了中国制造2025，为实现国家从制造大国向着制造强国迈进。工业生产中的2K-V型减速器起了重要的作用，在机械臂、机床、装配装置、搬运装置、纺织机械等领域得到了广泛的应用。国产减速器在近几十年得到了飞速发展，传动精度也得到大幅度的提高，但在一些高精度的产品中很难批量化生产，出现一致性差、传动精度不稳定等现象。因此研究2K-V型减速器传动精度势在必行，建立精准的理想虚拟样机模型和综合考虑误差的虚拟样机模型是动力学分析的基础。

2K-V型器减速器的独特结构形式和优越性能，受到了各国减速器制造厂家的青睐，从而2K-V型器减速器得到了迅速的发展，国内各大高校各大减速器厂家也在不断探索与研究。由于制造工艺、制造误差、装配误差等因素，造成了减速器一致性差和性能不稳定的情况。为了研究和分析这种情况，有必要对2K-V型器减速器进行实际测量，找出误差因素，通过理论与实际指导2K-V型器减速器的零部件的生产。本文主要基于高精度测量仪的测量数据，进行三维CAD建模，分析实际模型与理论模型，验证模型的正确性，为后续2K-V型器减速器动力学研究打下基础。

2008年张春亮等[1]通过三维参数化软件Pro/E对2K-V型器减速器进行零部件的参数化建模，进行了2K-V型器减速器虚拟样机的建立工作；2011年朱斌等[2]采用三维建模软件进行参数化建模并进行参数化装配，并结合了ANSYS分析软件生成了模态中性文件，为后续柔性体动力学打下基础；2013年蔡胜等[3]基于SolidWorks三维建模软件建立2K-V型器减速器虚拟样机并进行研究，得出了一些结论；2018年常安全等[4]建立了基于多体动力学仿真的2K-V型器减速器虚拟样机，得出相应的研究结论。以上虚拟样机的建立都是通过理论建模进行的动力学研究，本文提出一种新的模型建立方法，通过高精度测量仪测绘2K-V型减速器的真实零件，在三维CAD软件进行三维实体建模，通过高精度测量仪实际测量建立的三维模型与理论模型进行对比验证，验证样机的正确性，为今后研究2K-V型器减速器的动力学研究提供了一种可行的建模思路。

1 2K-V型减速器结构及传动比计算

随着我国工业的飞速发展，2K-V型减速器在农业、国防、机械臂、机床、装配装置、精密机械加工、搬运装置、纺织机械等领域得到了非常广泛的应用。由于2K-V型减速器结构和传动特性，给予了2K-V型摆线针轮减速器独特的优点和优势，这也是被世界各国所重视的重要原因。2K-V型减速器的优点主要有以下几个方面：1）在结构外形方面，体积小，结构比较紧凑，质量轻，与同等功率的普通减速器相比，2K-V型减速器减速器质量和体积要减少三分之二左右。2）在传动方面，2K-V型减速器运行平稳，无噪声，承载能力强，由于双摆线轮啮合齿数多，能够承受较强的冲击；传动比范围广，能够实现多级减速或者增速，正是这一特点，在机械臂得到了广泛的应用；传动效率高。3）在使用方面，由于摆线针轮的所有接触为滚动摩擦，故有比普通减速器更长的使用寿命。

1.1 2K-V型减速器的结构

2K-V型减速器结构相对比较复杂，为了更清晰地表述，绘制了结构简图（如图1），该机构为二级减速机构，第一级为减速机构为齿轮啮合减速机构，第二级减速机构为少齿差摆线针轮啮合机构。

图1 2K-V型减速器机构简图

1.2 2K-V型减速器的传动比计算

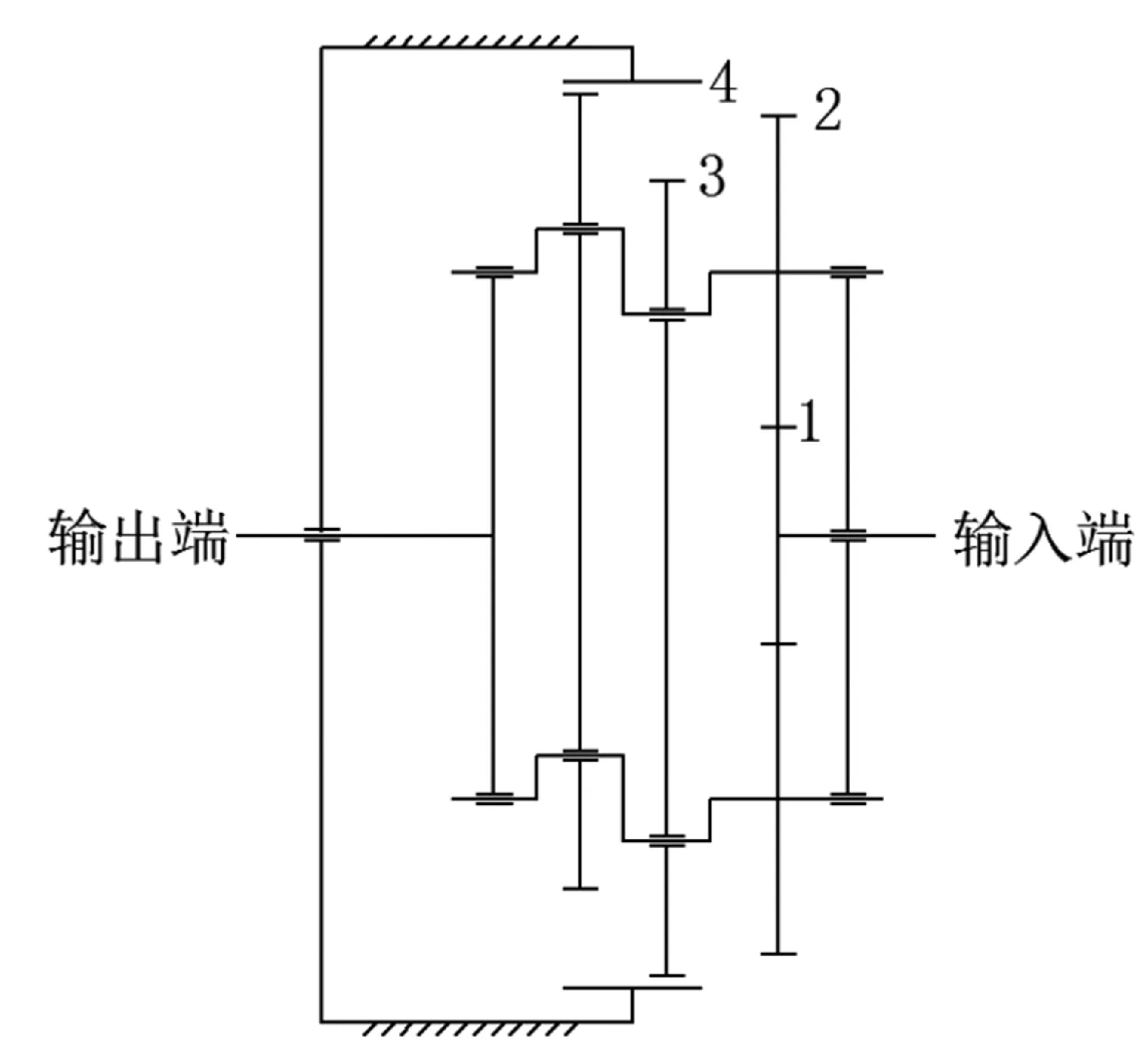
图2 2K-V型减速机传动结构简图

2K-V型型传动机构是一种二级传动减速机构，由太阳轮和行星轮组成的渐开线圆柱齿轮行星减速机构和摆线针轮行星减速机构组成。按照转化机构法计算2K-V型减速器的传动比。当输出入法兰盘（行星架）固定时，第一级传动比为

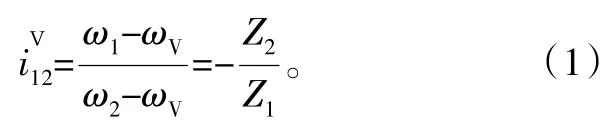
式中：ω1为太阳轮轴1的角速度；ω2为行星轮2的角速度；ωV为输出入法兰盘的角速度；Z1为太阳轮轴1的齿数；Z2为行星轮2的齿数。

当曲柄轴H*固定时，由于行星轮2和曲柄轴H*固定联在一起，ω2=ωH*,第二级传动比为

式中：ω3为输入轴3的角速度；ω4为行星轮4的角速度；Z3为输入轴3的齿数；Z4为行星轮4的齿数。

输出入法兰盘H作为输出件时，由输出入法兰盘H、曲柄轴H*和摆线轮3组成的三曲柄输出机构把摆线轮3的自转速度以1:1的速比传递至输出入法兰盘H，因此

当针轮壳体4固定，即为ω4=0，输出入法兰盘做输出构件时，联立式(1)、式(2)、式(3)可得输入轴1与输出入法兰盘H的角速度之比为

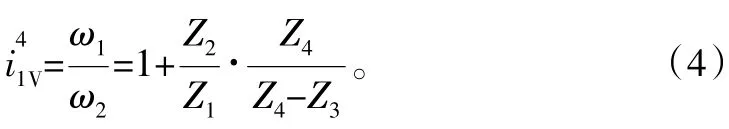
假如Z4-Z3=1，上式可以写成

当输出入法兰盘H固定，即为ωV=0，针轮壳体作为输出构件时：

联立式(1)、式(2)、式(6)可得输入轴1与行星架H的角速度之比：

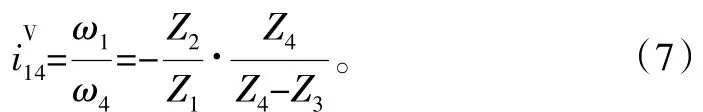
假如Z4-Z3=1，上式可以写成

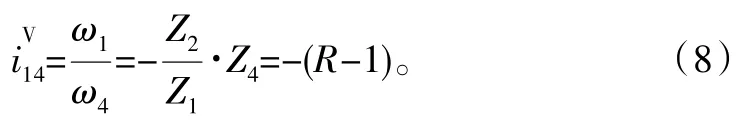
式中，“-”表示输入轴1与针轮壳体4的旋转方向相反。

通过对式(4)和式(7)分析易知，不管是用机架固定（即为针轮壳体固定），还是输出入法兰盘固定，2K-V型减速器的传动比可通过改变第一级两齿轮齿数比值Z2/Z1与第二级少齿差的两轮齿数比值Z4/（Z4-Z3）所决定，通过改变两级传动中的齿轮齿数可以得到不同的传动比。

2 2K-V型减速器理想模型的建立

表1 零件数量统计表

建立理想2K-V型减速机虚拟样机模型，为对比高精度测量仪测绘数据建立的虚拟样机模型进行验证。本文以2K-V型110E型减速器为研究对象，关键零部件主要参数如下:太阳轮齿数Z1=20,行星轮齿数Z2=55，模数为m=1.25 mm，压力角为α=20°，针齿数Zp=40，摆线轮齿数Zc=39，偏心距e=1.5 mm，针齿半径rrp=3.5 mm。2K-V型110E型减速器主要零部件的名称数量统计如表1所示。

基于CAD三维绘图软件对个零部件进行绘制，分别绘制太阳轮、3个行星轮、2个摆线轮，3个曲柄轴、输出入法兰盘、针齿壳、40个针齿三维实体模型，并对2K-V型关键零部件进行参数化，下面以齿轮这一零部件为例绘制其三维实体模型，该模型考虑齿轮变位，建立该模型初期需要用三维绘图软件输入公式分别计算齿轮分度圆直径、基圆直径、齿顶圆直径、齿根圆直径，然后用渐开线方程驱动，绘制齿轮的外围轮廓线，进行参数化建模如图3～图4所示。

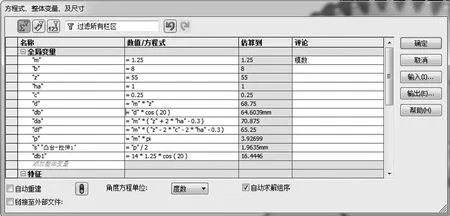
图3 行星齿轮参数化

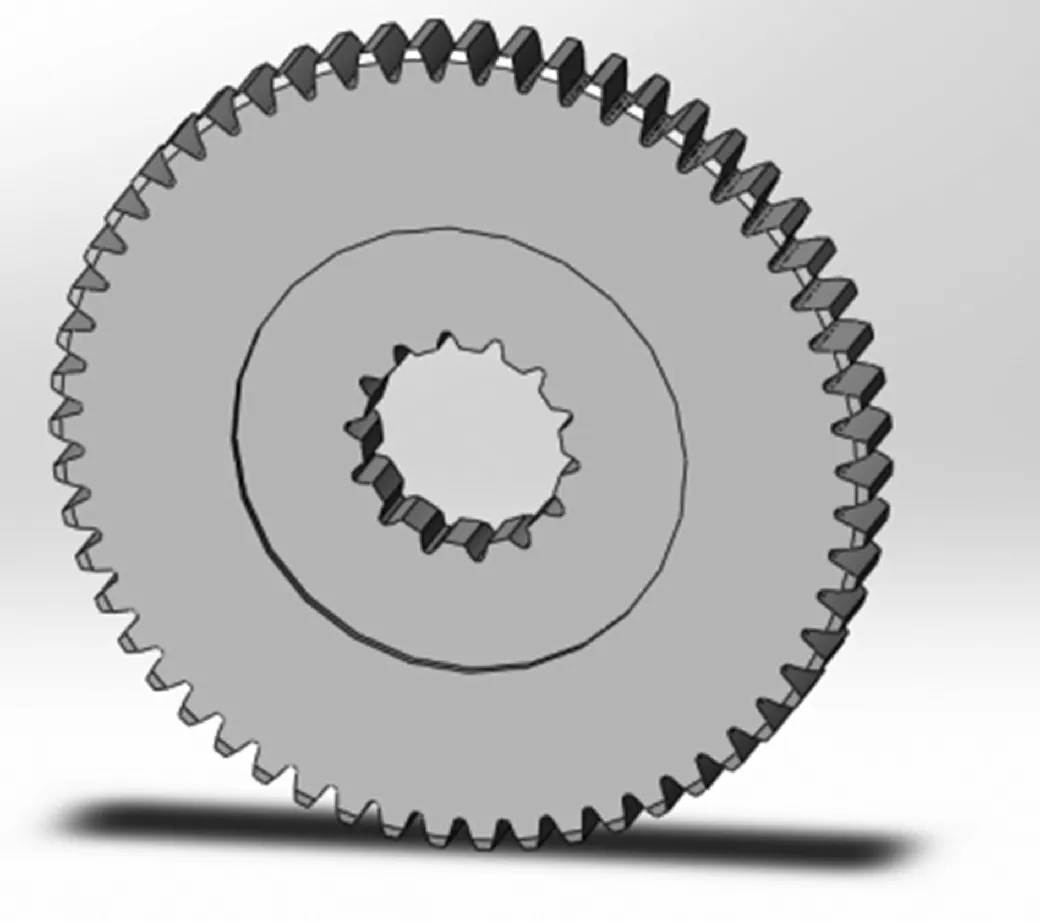
图4 行星轮三维模型

同样绘制其他零部件，实现部分关键零部件的参数化，方便模型的修改和修形，最终实现零部件的装配工作，为后续动力学分析做准备。

3 2K-V型减速器考虑误差模型的建立

清，然后选定坐标系开始测量，测量输出结果分为4种，分别为测量结果、测量值、拟合测量结果、拟合测量值。然后对一个零部件的一个单一测量数据输出，如图7～图9所示。

图5 高精度全自动影像测量仪

NIKEON高精度全自动影像测量仪VMZ-R4540（如图5），配置8段LED环形照明系统，从8个不同方向进行控制，测量效率较高；宽视场变焦光学系统适合测量许多大阶梯、深孔，高凸台等特征的低密度产品；图像自动对焦（AF）具有快速、高灵敏度的测量效果，可以更好地测量粗糙表面的平均高度、检测小尺寸深孔或陡峭表面深度。该测量仪的软件包容性强，支持CAD数据导入，测量结果到DXF数据实现脱机编程量测。该高精度测量仪的测量精度为0.1 μm，为后续的建模提供高精度数据，更大限度地反映真实性。

在建立考虑误差虚拟样机前期，需要对2K-V型型减速器各个零部件进行实际测量，实物如图6所示。由于零部件加载后上面有油污，为了更好更精准地测量零部件，需要对各个零部件进行两次清洗，第一遍采用煤油进行清洗，通过煤油清洗上面的油污，第二遍用酒精进行清洗，主要清洗零部件上的煤油，然后进行密封装袋，等待逐一测量。测量过程相对繁琐，一般零部件的测量过程是：将零部件放置在测量平台上，调节光源使其在测量区域显示高

图6 测量实物图

图7 测量结果图形绘制

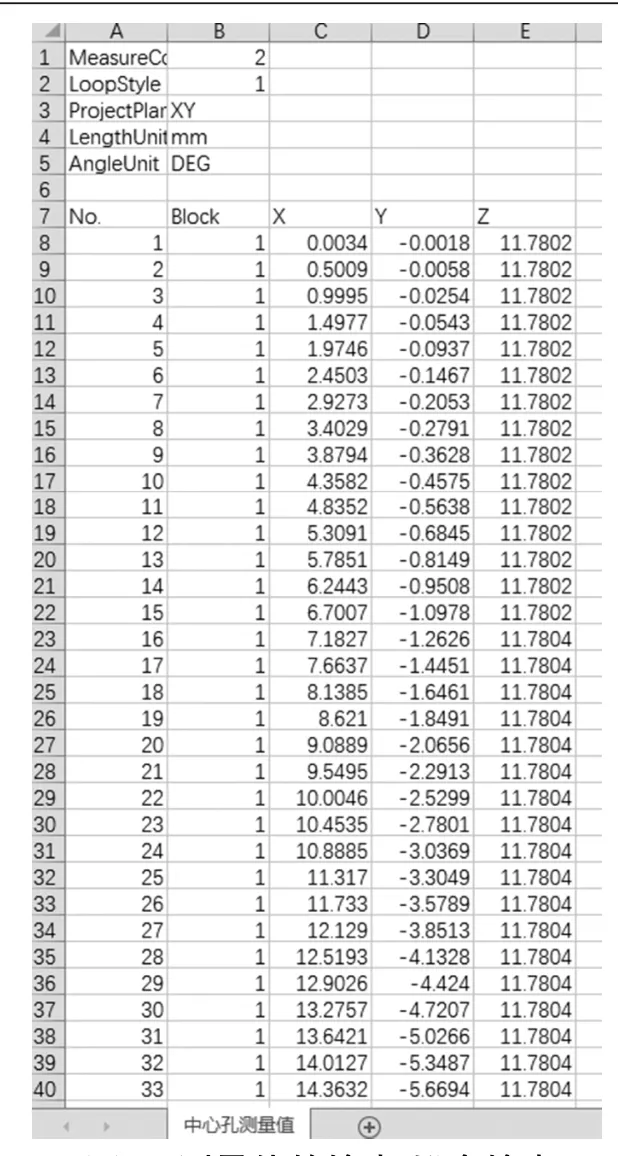
图8 测量值的输出/拟合输出

图9 拟合后测量偏差及其数据选取

为了更精准地反映模型的真实情况，选取摆线外围轮廓测绘较多的点数，以摆线轮测量值为例进行数据的整理汇总，将摆线轮A外围齿廓测绘的4490个点进行编辑，然后将数据导入CAD绘图软件中进行图形的绘制，绘制结果如图10 所示。同样将摆线轮中心轴孔、曲柄轴孔1、曲柄轴孔2、曲柄轴孔3测量数据导入进行三维实体建模，如图11所示。

针对画出的所有零部件实现装配，装配如图12所示。

图10 摆线轮齿廓二维图

4 2K-V型减速器系统等效动力学分析

为了综合校验建立减速器模型的正确性和可行性，建立2K-V型等效动力学模型，通过对比验证两种样机充分说明，基于高精度测量仪综合考虑误差的虚拟样机的正确性。由于减速器可以做减速装置，也可以做增速装置，常见一般为减速，有下面3种：针齿壳固定，太阳轮轴做输入，输出入法兰盘做输出；输出入法兰盘固定，太阳轮轴做输入端，针齿壳做输出端；太阳轮轴固定，针齿壳做输入端，输出入法兰做输出端。增速装置将上述3种输入端输出端交换即可，共有6种传动方式。下面以减速装置的前2种为例进行系统等效动力学分析，在建立动力学模型时做了如下简化处理：忽略轴承、卡簧垫片，螺栓螺母；忽略支承、齿轮系统的弹性及传动系统阻尼。

减速装置中针齿壳（输出入法兰盘固定）固定时，2KV型减速器转动构件主要有太阳轮、行星轮、摆线轮、输出入法兰盘（针齿壳）、曲柄轴。针对齿壳固定时，太阳轮、输出入法兰盘只有自转，3个行星轮、3个曲柄轴既有自转又有公转，1个摆线轮既有自转又有公转；当输出入法兰盘固定时，太阳轮、针齿壳、行星轮、曲柄轴只有自转，两个摆线轮只有公转。

图11 摆线轮三维模型

图12 2K-V型减速器装配体

4.1 等效动力学方程式的建立

下面对减速器主要零部件的转动惯量、角速度分别做以下定义，太阳轮轴自转时的转动惯量为J1、角速度为ω1；行星轮1自转时转动惯量为J2、角速度为ω2，公转时转动惯量为J3、角速度为ω3；行星轮2自转时转动惯量为J4、角速度为ω4，公转时转动惯量为J5、角速度为ω5；行星轮3自转时转动惯量为J6、角速度为ω6，公转时转动惯量为J7、角速度为ω7；曲柄轴1自转时转动惯量为J8、角速度为ω8，公转时转动惯量为J9、角速度为ω9；曲柄轴2自转时转动惯量为J10、角速度为ω10，公转时转动惯量为J11、角速度为ω11；曲柄轴3自转时转动惯量为J12、角速度为ω12，公转时转动惯量为J13、角速度为ω13；摆线轮A自转时转动惯量为J14、角速度为ω14，公转时转动惯量为J15、角速度为ω15;摆线轮B自转时转动惯量为J16、角速度为ω16，公转时转动惯量为J17、角速度为ω17;输出入法兰盘自转时转动惯量为J18、角速度为ω18；针齿自转时转动惯量为J19、角速度为ω19；针齿壳自转时转动惯量为J20、角速度为ω20。

下面建立单自由度机械系统运动方程，根据动能定理，机械系统某一瞬间其总动能的增量等于该瞬间内作用于该机械系统的各个外力所做的功之和，由此可得

当针齿壳固定时，系统的运动方程为

为了计算方便，对于理想虚拟样机模型计算，可以做下面简化：

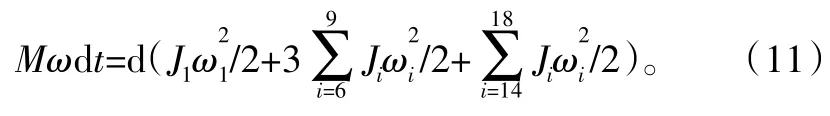
当输出入法兰盘固定时，系统的瞬间动能的增量为

对于理想虚拟样机模型计算，可以做如下简化：

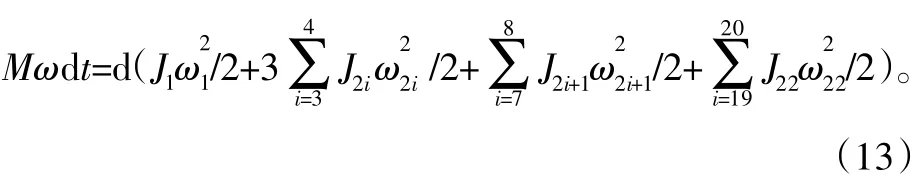
建立2K-V型减速机等效动力学模型[5]，现取太阳轮轴为等效构件，则有

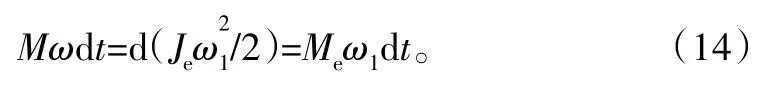
可以得出式(10)、式(11)、式(12)、式(13)的等效力矩和等效转动惯量如下：

4种方程等效力矩为

当针齿壳固定时，系统运动方程的等效转动惯量为

为了计算方便，对于理想虚拟样机模型计算，简化后的等效转动惯量

当输出入法兰盘固定时，等效转动惯量为

对于理想虚拟样机模型计算，简化后等效转动惯量：

4.2 虚拟样机的验证

表2 自转转动惯量对比 kg·m2

通过CAD三维建模软件仿真计算，由于金属材质，统一选为普通碳钢。计算2K-V型减速器关键零件的自转转动惯量，如表2所示。

表3 公转转动惯量对比 kg·m2

由平行轴定理[6]可知，公转时的转动惯量为

式中：m代表物体质量；l代表各个零件中心轴线到针齿壳轴线的距离，可以得出理论和实际公转时的转动惯量。曲柄轴按照理论考虑，算得：

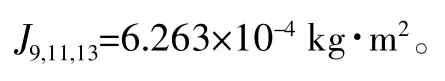
2K-V型减速器角速度之间的关系：

当针齿壳固定时：

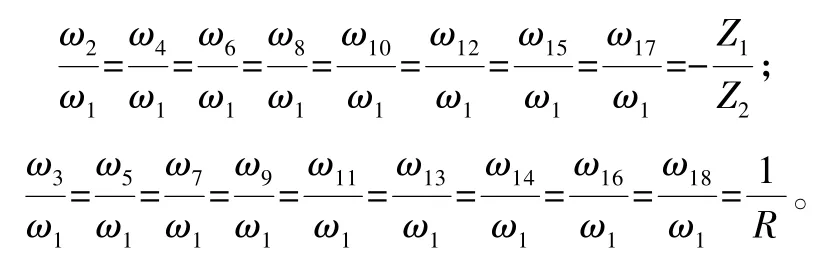
当行星架固定时：

其中：Z1,Z2,R分别为减速器太阳轮轴的齿数、行星轮的齿数、速比值。

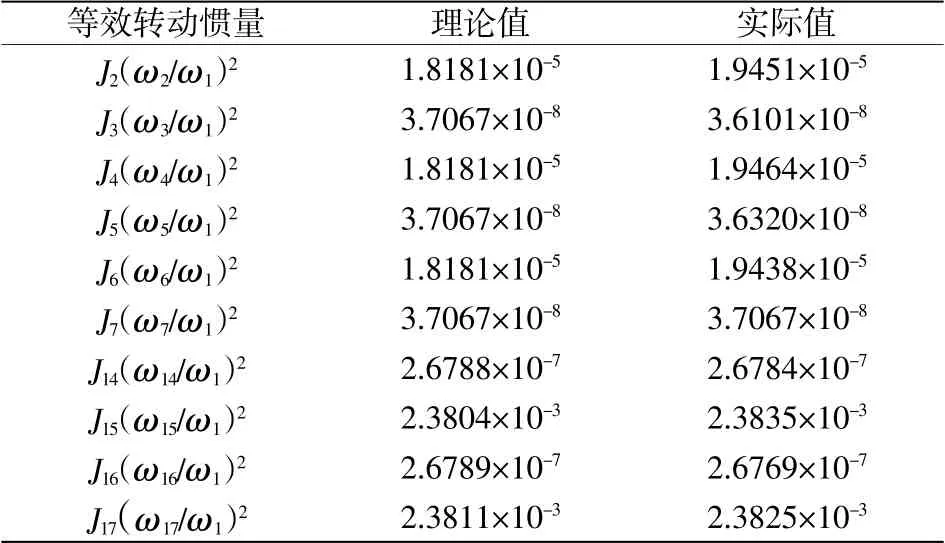
表4 等效转动惯量对比 kg·m2

曲柄轴，输入输出法兰盘、针齿、针齿壳按照理想值考虑（单位：kg·m2）：

经过计算可以得到以太阳轮轴为等效构件，当针齿壳固定时等效转动惯量理论值和实际值分别为（单位：kg·m2）：Je1=4.8218×10-3；Je2=4.8375×10-3。

当行星架固定时等效转动惯量理论值和实际值分别为（单位：kg·m2）：

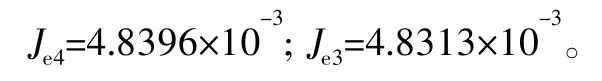
5 结 论

本文建立了2K-V型减速器系统等效动力学模型，经分析针齿壳固定、输出入法兰盘固定两种情况，得出理论与实际等效转动惯量的相差值分别相差0.326%、0.172%，充分验证了用高精度测量仪测绘数据建模的合理性和准确性，为下一步模型动力学分析打下了基础，为后续2KV型减速器动力学研究提供一种可行的建模思路和方法。