新型三元层状硼化物Cr4AlB4的物相稳定性和力学行为分析

齐欣欣, 宋广平, 尹维龙, 王明福, 赫晓东, 郑永挺, 王荣国, 柏跃磊

新型三元层状硼化物Cr4AlB4的物相稳定性和力学行为分析

齐欣欣1, 宋广平1, 尹维龙1, 王明福2, 赫晓东1, 郑永挺1, 王荣国1, 柏跃磊1

(1. 哈尔滨工业大学 特种环境复合材料技术国家级重点实验室, 哈尔滨 150080; 2. 北京动力机械研究所, 北京 100074)

Cr4AlB4是一种近期发现的三元层状硼化物MAB相陶瓷。该材料可形成具有保护性的氧化膜, 在高温结构材料领域有巨大应用潜力。本工作采用基于第一性原理的“线性优化法”和“键刚度”理论模型分别研究了Cr4AlB4的物相稳定性和力学行为。声子谱中没有虚频出现, 表明Cr4AlB4具有本征稳定性。而与其它Cr-Al-B系内的竞争相相比, Cr4AlB4具有最低的能量, 表明其在热力学上也是稳定的。采用“键刚度”模型对化学键刚度的定量计算显示, Cr4AlB4中Cr和B以及B和B原子之间形成了强共价键, 而Cr和Al原子则形成相对较弱的Cr-Al(625 GPa)和 B-Al(574 GPa)键。Cr4AlB4可以看成是由强共价键紧密连接在一起的Cr-B结构单元, 被弱Cr(B)-Al键分割而成的层状结构, 与MAX相结构类似。Cr4AlB4具有类似于MAX相的高损伤容限和断裂韧性。

MAB相; 密度泛函理论; 物相稳定性; 力学性能

超高温陶瓷(Ultra-High Temperature Ceramics, UHTCs)凭借优良的高温性能在航空航天领域具有广阔的应用前景, 其中二元硼化物更是具备了较好的综合性能[1]。然而, 二元硼化物的本征脆性和较差的抗氧化性是限制其实现应用的主要障碍。近二十年来, 在二元碳化物、氮化物中插入主族原子形成的M+1AX相化合物(M为过渡金属元素, A是IIIA或IVA主族元素, X是C或N,=1-3)由于具备高断裂韧性、高损伤容限、良好的抗热震和抗氧化性能而备受人们关注[2]。受MAX相的启发, 在二元硼化物中插入单层或双层主族原子如Al原子也可形成被称为“MAB相”的三元层状过渡金属硼化物[3]。

大部分MAB相陶瓷早在20世纪60年代就已经被发现[4-5], 但直到2013年细致的结构和性能表征才陆续开展[6]。2015年Ade等[3]合成出一系列的MAB相化合物单晶并对其结构和硬度进行了研究。而最近的研究工作显示MoAlB[7]和Fe2AlB2[8](典型的MAB相化合物)具有较高的断裂韧性和损伤容限以及良好的抗氧化性能, 这对其潜在的结构应用极为重要。Cr-Al-B系MAB相化合物在氧化过程中形成致密的Cr2O3或Al2O3氧化膜, 具有良好的抗氧化性能, 因而受到了广泛关注[9-11]。具有不同晶体结构的Cr2AlB2、Cr3AlB4和Cr4AlB6很早就被发现[12], 该体系也是目前发现MAB相材料最多的体系。最近, 一种新型的MAB相化合物Cr4AlB4在该体系中被发现[13], 其结构不同于之前发现的任何一种MAB相化合物。第一性原理研究工作预测了它的晶体结构、电子结构、化学键合、理论强度和以及热膨胀行为等[14]。

对结构陶瓷来说, 力学性能特别是损伤容限和断裂韧性对其工程应用极其关键。而晶体结构对材料的宏观力学行为具有重要影响。一般认为MAX相材料中的高损伤容限和高断裂韧性即来源于其层状结构和层间的弱化学键结合[2]。由于目前尚不能制备高纯块体Cr4AlB4材料而无法对其力学行为进行实验表征, 第一性原理方法具有成本低、效率高、可精确计算材料基态性质的优点, 已被广泛应用于材料性能表征[15-16], 本工作采用第一性原理方法对Cr4AlB4的物相稳定性、压缩和力学行为进行分析, 为深入理解和认识晶体结构对MAB相宏观行为的影响和进一步实验研究提供理论指导。

1 计算参数及模型设置

1.1 通用参数

本研究利用VASP[17]软件包计算Cr4AlB4的平衡晶格常数和其它性能。电子和离子之间的作用选择PAW方法描述, 其中Cr原子把p电子作为半芯态来处理, Cr、Al和B原子选取的价电子分别为3p63d54s1、3s23p1和2s22p1。先选取不同的交换关联泛函包括广义梯度近似(GGA[18]-PBE, RPBE[19], PW91[20])和局域密度近似(LDA)来寻找与实验值最接近的结果, 对其它参数选取计算精度最好的交换关联函数进行计算。平面波矢的截断能选取为450 eV, 布里渊区k点积分采用Monkhorst-Pack方法, 网格设定为13×2×13。经测试, 该截断能和k点网格使总能变化小于1 meV/atom。计算态密度时, k点网格加密设定为39×6×39。结构优化所用的收敛判据为: 离子弛豫过程中的总能量变化小于10–5eV, 电子弛豫过程中总能变化小于10–6eV, 作用于原子的力小于0.01 eV/nm。

力常数矩阵和声子振动频率利用基于有限位移法的PHONOPY软件包计算得到, 而其中的电子结构计算则由VASP完成。具体方法为: 在Cr4AlB4晶胞中每个非等同原子上施加一套独立的小位移, 然后通过电子结构计算得到原子间的Hellmann- Feynman作用力, 进一步得到原子间的力常数矩阵。本文构造了一个2×1×2超胞并采用7×4×7的k点网格用于计算扰动原子产生的力。收敛条件是总能量的变化小于10–8eV

1.2 物相稳定性

本研究主要从本征稳定性和热力学稳定性角度研究Cr4AlB4的物相稳定性。本征稳定性指的是结构的吉布斯自由能对于小变形处于一个极小值附近。这是任何一个化合物或结构稳定存在的必要条件。在实际研究工作中, 可以通过考察晶格动力学(声子)行为来加以确定; 稳定结构中不应该出现负频率的振动模态, 因为这意味着所研究的结构并不处于局域能量极小值。

热力学稳定性是指与体系中其它竞争相或者竞争相(结构)组合相比应处于能量最低状态。Dahlqvist等[21]提出了一种研究MAX相稳定性的方法: 它利用线性规划法来寻找某一给定元素组成M,A和B结构中最稳定的竞争相组合(能量最低)。本文用该方法研究MAB相的稳定性, 可用下式表示:

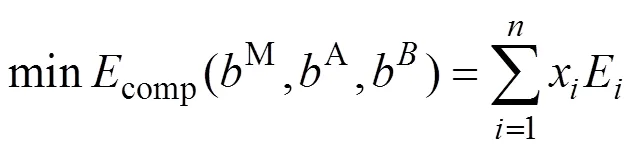
其中,x和E分别是化合物的数量和对应的能量, 并且受线性规划最小值约束。考虑到质量守恒, 则有:

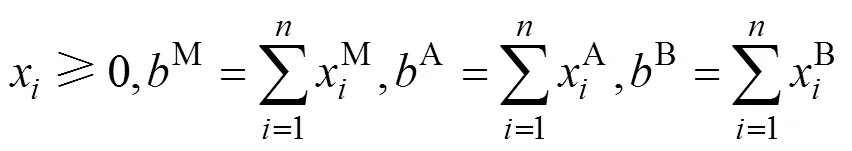
对Cr4AlB4,M=4,A=1,B=4。因此, 任一MAB相相对于所确定的最具竞争性相组成的形成焓可根据下式计算:

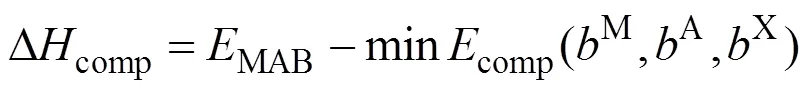
根据形成焓Δcomp的正负来评估所研究化合物的热力学稳定性: 若Δcomp为正, 则所研究的MAB相不稳定; 反之, 则稳定。

1.3 “键刚度”模型

假设化学键在静水压力作用下的变形规律类似于弹簧而满足胡克定律, 其中刚度用于定量表征化学键强度。根据优化后的晶格参数和坐标可以很方便地计算原子间距离(键长,)与静水压力之间的关系。由于键强随原子间距离的增加而变弱, 所以相对键长0(0为0 GPa的键长度)随的变化用二阶多项式拟合, 该曲线的斜率定义为1/, 其中是化学键刚度[22]:

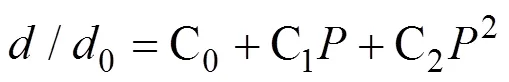
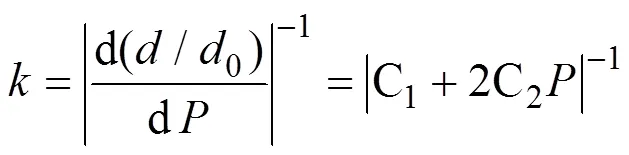
其中C(=0, 1, 2)是二阶多项式拟合系数。

1.4 二阶弹性常数和弹性模量

二阶弹性常数ij是通过对晶格进行六次有限变形后根据应力应变关系拟合来确定的。默认步长为0.0015 nm。对于每个应变分量, 施加两个正(0.015, 0.003)和两个负(–0.015, –0.003)应变, 然后根据计算应力随应变的函数线性拟合确定弹性刚度。工程弹性常数包括体积模量(), 剪切模量(), 杨氏模量()和泊松比()根据Voigt近似从二阶弹性常数确 定[23]。德拜温度(D)的计算方法详见文献[24]。

2 结果与讨论

2.1 晶体结构

采用不同交换关联泛函(GGA-PBE、GGA-RPBE、GGA-PW91、LDA)计算获得的平衡晶格参数如表1所示。LDA所算出的晶格常数最小, 且明显小于实验值。需要指出的是, LDA通常低估晶格常数。GGA的计算结果与实验值较为接近, 但都小于实验值, 这与对MoAlB的计算结果并不相同[25], 其中RPEB的计算结果与实验值最为接近(误差小于1%), 故在之后的计算中均采用RPBE。根据表1还可以发现随着Al层插入到Cr-B结构中, 晶格常数和由CrB的0.2924和0.2911 nm增加到0.29334和0.29551 nm, 并且Cr4AlB4与其它Cr-Al-B系MAB相具有相近的密度[26]。实际上, 之前的结果也显示了Cr-B层片数的增加并不显著提高Cr-Al-B系MAB相的密度[26]。

图1为Cr4AlB4及CrB的晶体结构, 图中显示Cr-B层沿轴方向被Al单原子层分离。换句话说, Cr4AlB4看作二元硼化物沿轴方向插入单层铝原子而形成的。Cr4AlB4还可以描述为类似于MAX相的层状结构: 结合力较弱Cr-Al原子层与强共价键结合的Cr-B层交错堆叠。相邻原子之间的键长列于表2(在图1中标记的相关原子), 并对二元化合物CrB的相应数据进行了比较。对于Cr4AlB4, Cr-B层与CrB具有类似的构型, B-B链与CrB相比有轻微的扁平化, 在Cr4AlB4中B1-B2和Cr1-B2键长分别为0.1771和0.2180 nm(CrB中分别为0.17841和0.2212 nm)。而两层Cr-B之间的距离明显增加, Cr2-B3的键长为0.2288 nm。Cr4AlB4与其它已知的Cr-Al-B系MAB相明显不同的一点是其它MAB相Cr和B原子的构型取决于Cr-B层中的位置: 在边缘处, 构型与CrB相似, 在Cr-B层中, 原子采用CrB2的结构, B原子形成平面的六方环[26]。

2.2 物相稳定性分析

Cr4AlB4的声子色散曲线和态密度如图2所示。在声子谱中没有虚频出现, 这意味着Cr4AlB4的吉布斯自由能对于小变形处于一个极小值附近, 表明其是本征稳定的。如图2所示, 14 THz以上的高频声子态主要是由B原子的振动引起的, 而低频的晶格振动则主要归因于Cr和Al原子。B原子的高频率是由于它的强化学键合和低原子质量。Cr原子由于其高质量导致其具有较低的频率, 而相反地, 由于具有较弱的键合(尽管它的质量较低), Al原子占据低频的相似范围。这与其它Cr-Al-B系MAB相的计算结果相似[26]。

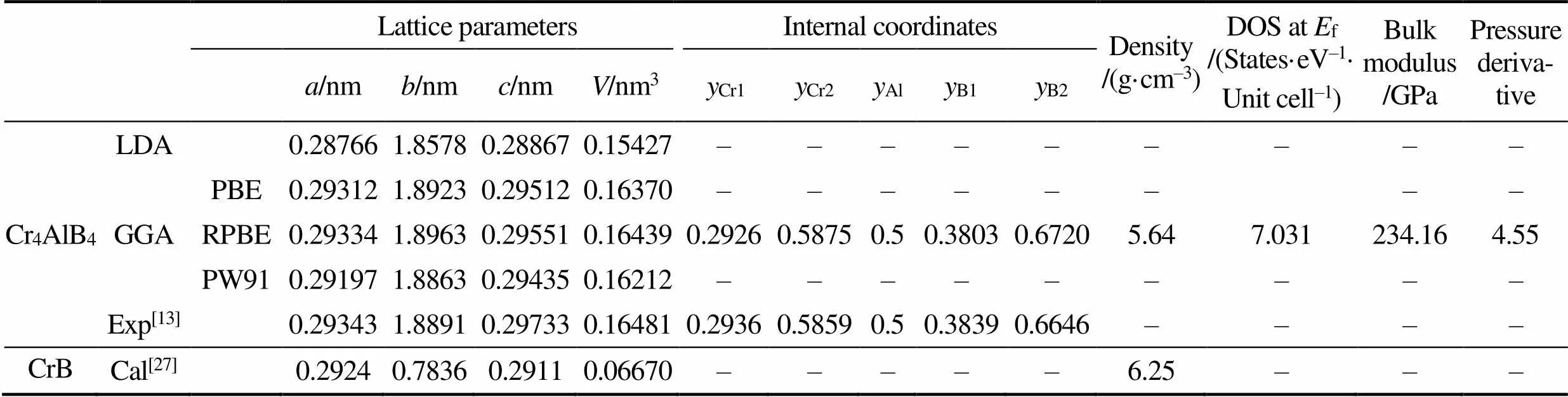
表1 Cr4AlB4及CrB晶格参数及基本属性

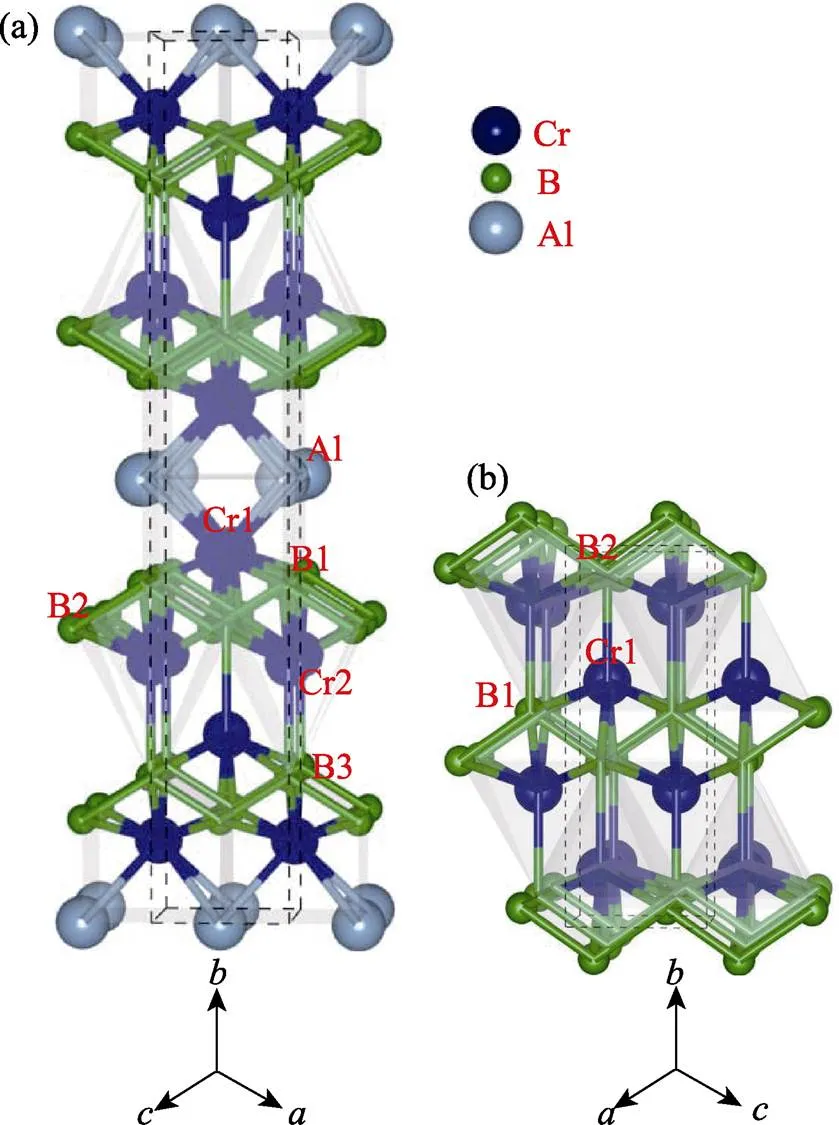
图1 Cr4AlB4(a)和CrB(b)的晶体结构

Cr4AlB4can be regarded as CrB with Al monolayer inserted along the b axis

通过应用Dahlqvist等[21]的方法来评估Cr4AlB4的热力学稳定性, 结果如表3所示。可以发现, Cr4AlB4的Δcomp小于0, 证明Cr4AlB4是热力学稳定的。值得注意的是, Cr4AlB4的Δcomp小于Cr2AlB2的Δcomp, 说明Cr4AlB4具有更高的热力学稳定性, 这也解释了在合成实验时, Cr2AlB2的合成温度低于Cr4AlB4[13]。

2.3 可压缩行为与键刚度

通过研究材料的可压缩行为可以探究材料的各向异性、化学键合和高压稳定性等。因此, MAX相的可压缩性一直是重要的实验[28]和理论研究[29]方向。基于密度泛函理论的第一性原理研究方法被广泛应用于研究高压下的体积模量、化学键合和相稳定性。图3(a)显示了Cr4AlB4的晶胞体积随静水压力的变化关系, 该曲线可用Birch-Murnaghan方程[30](状态方程)表示:

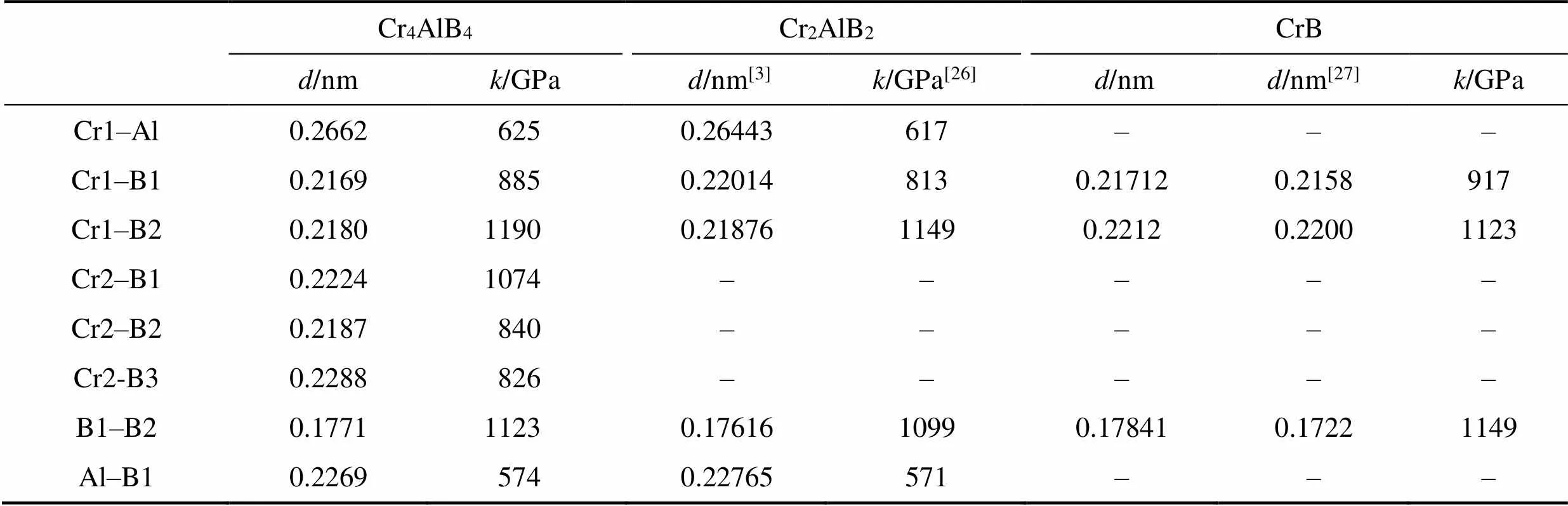
表2 Cr4AlB4、Cr2AlB2以及二元硼化物CrB的键长和键刚度

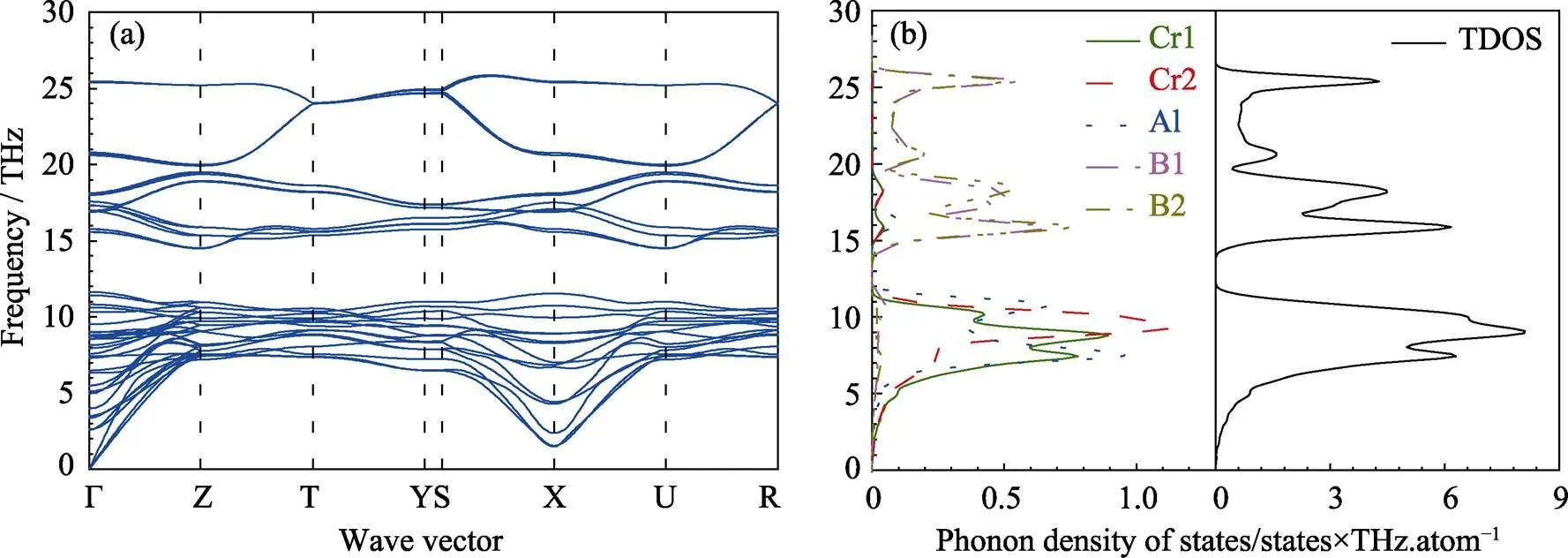
图2 Cr4AlB4沿高对称点方向的声子色散曲线(a)和态密度(b)

表3 Cr4AlB4的形成焓ΔHcomp, ΔHcomp< 0的相以粗体表示

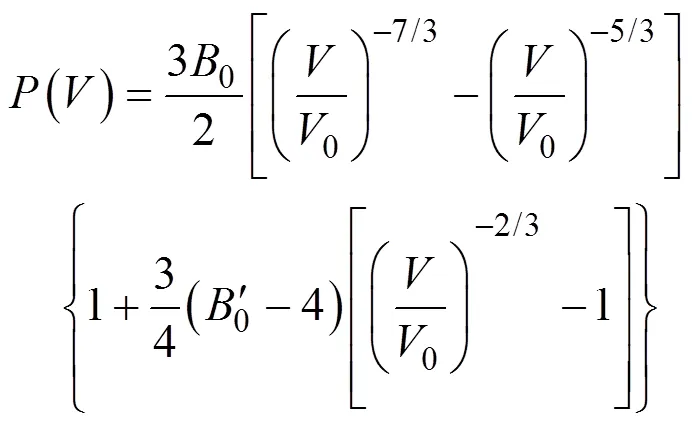
式中,为晶胞体积,0为体积模量,'0为压力导数,0为0 GPa时的晶胞体积。通过拟合该方程可获得Cr4AlB4的0及'0分别为234 GPa和4.55。

表2列出了采用“键刚度”模型计算出的在0 GPa时化学键刚度。Cr4AlB4中刚度最低的键为B1–Al键(574 GPa)。Cr–B键的强度与它们在Cr–B结构单元中的位置有关: 在层的边缘, Cr1原子采用与CrB中相似的结构, 更接近于六个相邻的B原子。Cr1–B2具有与CrB中相似的刚性, 并且是Cr4AlB4中刚度最大的键; 朝向Cr–B平板的中心位置, Cr–B键变得更软。

为了进一步深入理解Cr4AlB4的化学键合, 本工作研究了它的态密度, 电荷密度分布和电荷转移情况, 如图4、图5和表4所示。通过图4中Cr4AlB4的原子分波态密度可以看出在能级较低处(–13~ –9 eV), 主要由B1/2-2s态组成, 表明B–B共价键的高强度。在较高能量下, B-2p和Cr-3d的分波态密度在–6 eV至–3.5 eV的区域重叠, 具有重合峰, 表明这些轨道之间强烈的杂化。杂化区域的宽能量范围和高态密度则意味着相对较强的Cr–B共价键。在–3.5 eV和–2 eV之间, Al-p、B1-p和Cr1-p轨道之间还有一个重叠区域, 这意味着在Al和B1之间及Al和Cr1具有弱的化学键。类似的, CrB在–6 eV至 –3 eV区域B-2p和Cr-3d轨道之间发成重叠, 意味着相对较强的Cr–B共价键。可见, DOS的分析结果与键刚度模型的分析结果一致。

通过图5可以发现B原子与B原子之间存在明显的电荷堆积现象, 表明B–B键为较强的共价键。而Cr原子与B原子之间的电荷堆积情况却不完全相同, 其中Cr1原子与B2原子, 及Cr2原子与B1原子之间电荷堆积最为强烈, 而Cr2原子与B3原子之间电荷堆积情况最弱, 这与Cr–B键刚度计算结果(表2)一致。对Cr4AlB4的Bader电荷分析表明在Cr–B层层间电荷转移情况与CrB相似, Cr原子失去0.76个电子而B原子得到0.74个电子; 而在Cr–B层边缘, 由于Al原子的插入形成Cr–Al键和B–Al键, Cr原子失去电子变少, 减为0.39个, B原子得到电子变多, 增加到1.15个, 其中Al原子失去1.48个电子用于形成Cr–Al键和B–Al键(见表4)。

图3 压力对Cr4AlB4的归一化体积V/V0及归一化晶格常数a/a0, b/b0和c/c0 (a)和归一化键长d/d0 (b)的影响

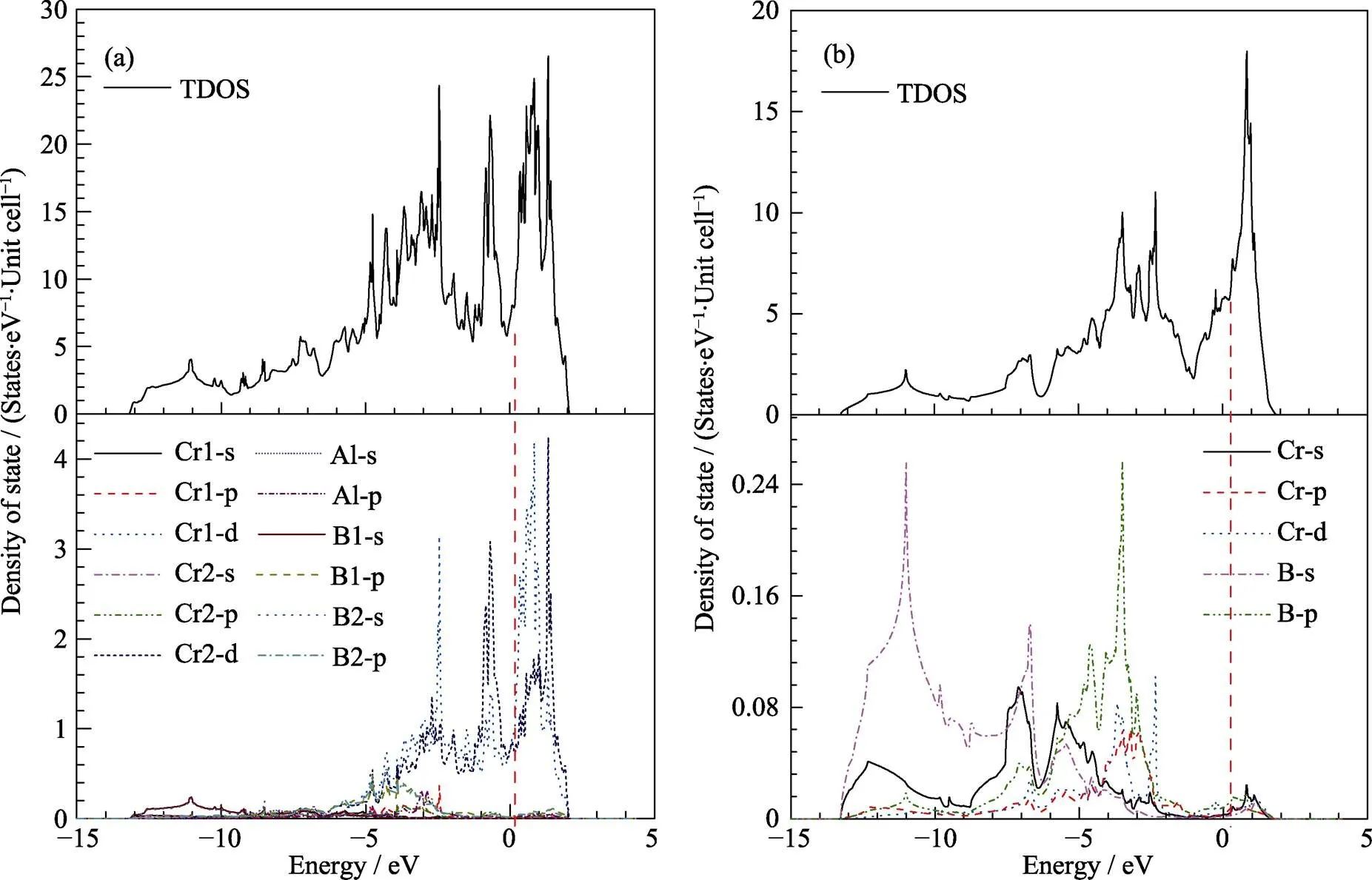
图4 Cr4AlB4 (a)和CrB (b)的态密度及分波态密度

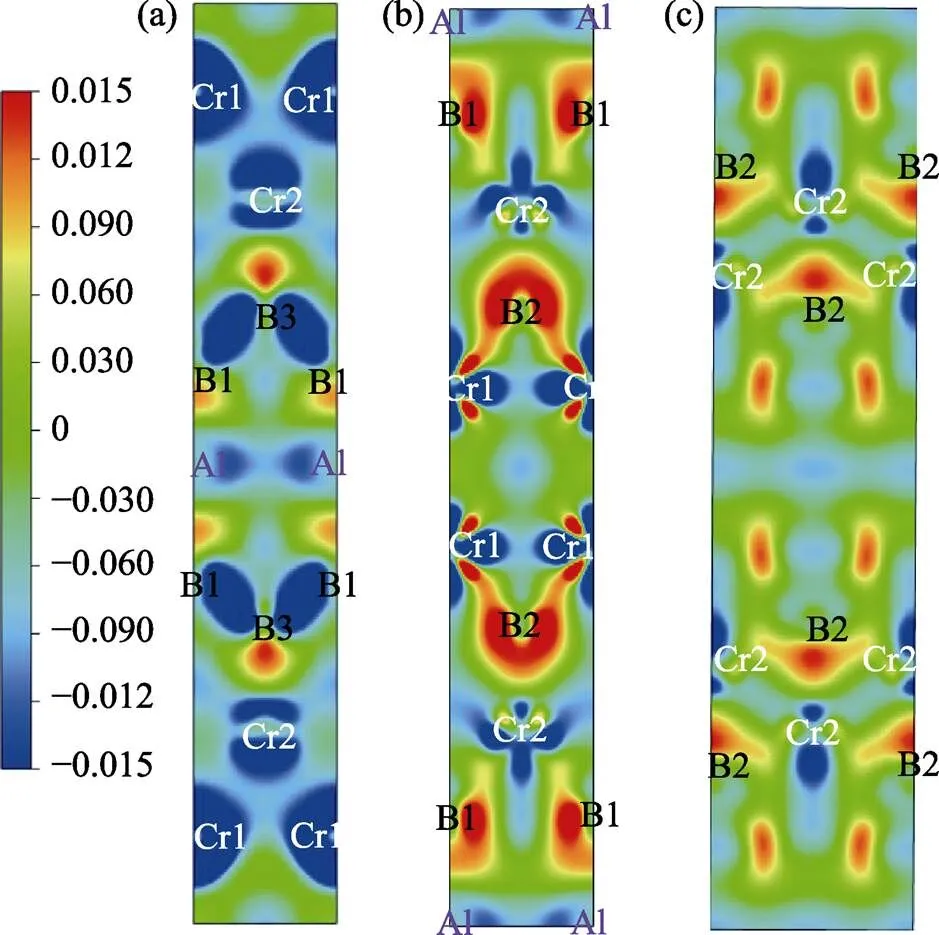
图5 Cr4AlB4在(001) (a)、(100) (b)和(101) (c)平面上的差分电荷密度

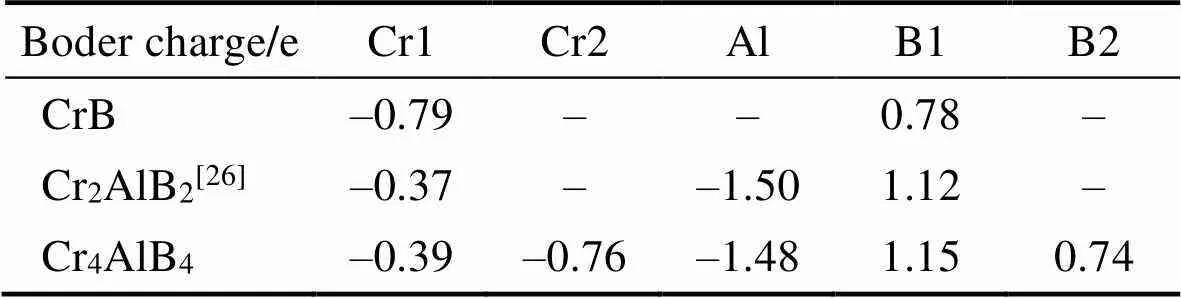
表4 Cr4AlB4, Cr2AlB2 和 CrB的贝德电荷分析

对MAX相的研究表明较弱的M–A键在其非凡力学行为中扮演了关键角色, 如高断裂韧性和损伤容限、低硬度、微尺度塑性变形等[31]。采用键刚度模型研究表明, 对包括MAX和MAB相的三元层状化合物陶瓷来说, 最弱化学键刚度与最强化学键刚度的比值与其宏观力学行为密切相关[25]: 当该比值大于1/2时, 这类陶瓷材料表现出典型脆性陶瓷的低损伤容限和断裂行为, 如三元碳化物(MC)Al3C2和(MC)Al4C3陶瓷[32]; 而当该比值小于1/2时, 这类陶瓷则表现出高损伤容限和高断裂韧性, 如MoAlB和典型的MAX相陶瓷[33-34]。

如表2所示, Cr4AlB4中刚度最低的键为B1–Al键和Cr–Al键, 与MAX相的M–A键相似。其中B1–Al键(574 GPa)和Cr1–Al键刚度(625 GPa)分别是最强的Cr1–B2键刚度(1190 GPa)的0.48和0.52倍。因此可以预见, MAX相中存在的反常力学行为也应该存在于Cr4AlB4中。最近对MoAlB的理论工作也得出了类似的结论[25], 并且与在实验观察到的高损伤容限一致[7]。

表5 Cr4AlB4的二阶弹性常数(cij/GPa)、体积模量(B/GPa)、剪切模量(G/GPa)、杨氏模量(E/GPa)、泊松比(μ)和德拜温度(θD/K)

2.4 弹性性能

晶体的弹性刚度决定了其对平衡位置附近的应变(或应力)的响应, 表5为Cr4AlB4的二阶弹性常数及工程弹性性能, 并将其与MAB相Cr2AlB2、MoAlB, 二元硼化物CrB和MAX相化合物Cr2AlC进行对比。11、22、33分别表示对主应变11、22和33具有的正变形阻力。11具有最大值(594 GPa),22具有最小值(472 GPa)。这与可压缩性的研究结果一致(图3)。其原因是由于B–B键的高刚性, 具有最大弹性常数方向应平行于B–B锯齿形/六角形链, 对应Cr4AlB4的轴方向。

同CrB相比, Cr4AlB4的11略大而22,33略小, 其原因是Cr4AlB4的轴方向为较强的B–B共价键(1123 GPa)折叠方向, 而CrB为轴方向。若选取相同方向, CrB的二阶弹性常数大于Cr4AlB4, 因为较弱的Cr–Al键(625 GPa)和B–Al键(574 GPa)使其弹性常数减小。Cr4AlB4的剪切变形值44、55、66与CrB相比也略有减小。与MAB相的Cr2AlB2相比, Cr4AlB4的二阶弹性常数较大, Cr2AlB2为单层的Cr–B层, 而Cr4AlB4为双层, Cr–B层具有较高的刚度。

表5还列出了Cr4AlB4的工程弹性常数, 包括泊松比()和体积模量(), 杨氏模量()和剪切模量(), 根据弹性常数ij计算。Cr4AlB4的体积模量(), 杨氏模量()和剪切模量()高于同为MAB相的Cr2AlB2和MoAlB, 但低于二元硼化物CrB。此外, Cr4AlB4与Cr2AlB2及CrB有着相近的泊松比, Cr2AlC明显高于三者。/比通常用于描述材料的延展性或脆性, 低/表示较好的延展性, 根据Pugh标准划分临界值为0.57[35]。Cr4AlB4的/比值为0.79, 大于0.57表明其属于脆性材料, 硬度较高。但对大部分三元层状化合物MAX相及MAB相的分析并不可靠, 例如对MoAlB的分析中, 其/较高但仍具有较好的损伤容限[25]。随着Al原子的插入, 德拜温度显著降低。德拜温度对应于晶格振动的最高频率, 这实际上是晶体内键合强弱的反映。这表明Cr4AlB4中的平均键合应弱于CrB, 并具有较大的热膨胀。

3 结论

本研究采用基于第一性原理的“线性优化法”和“键刚度”理论模型分别研究了Cr4AlB4的物相稳定性和力学行为。

1) Cr4AlB4在声子谱中并未出现虚频, 表明其具有本征稳定性。且高频的声子频率几乎被B原子占据, 而Cr和Al声子态的频率总是在较低位置。

2) Cr4AlB4与其他Cr-Al-B系竞争相相比, 具有最低能量, 处于热力学稳定状态。

3) 较强的B–B共价键导致了Cr4AlB4可压缩行为的各向异性, 其中轴的抗压能力最好,轴的抗压能力最差。

4) Cr4AlB4中刚度最低的键为最强键的0.48倍, 因此本文预测Cr4AlB4中也具有类似MAX相的高损伤容限和断裂韧性。

5) 随着Al原子插入CrB形成Cr4AlB4, 弹性常数略有降低。德拜温度显著降低则表明晶体内键合的减弱。

[1] FAHRENHOLTZ W G, HILMAS G E, TALMY I G,Refractory diborides of zirconium and hafnium., 2007, 90(5): 1347–1364.

[2] BARSOUM M W. The M+1AXphases: a new class of solids; thermodynamically stable nanolaminates., 2000, 28(1): 201–281.

[3] ADE M, HILLEBRECHT H. Ternary borides Cr2AlB2, Cr3AlB4, and Cr4AlB6: the first members of the series (CrB2)CrAl with= 1, 2, 3 and a unifying concept for ternary borides as MAB-phases., 2015, 54(13): 6122–6135.

[4] JEITSCHKO W. The crystal structure of Fe2AlB2., 1969, 25(1): 163–165.

[5] NOWOTNY H, ROGL P. Ternary Metal Borides. Berlin Heidelberg: Springer. 1977: 413–438.

[6] TAN XIAOYAN, CHAI PING, THOMPSON COREY M,Magnetocaloric effect in AlFe2B2: toward magnetic refrigerants from earth-abundant elements., 2013, 135(25): 9553–9557.

[7] KOTA S, ZAPATA-SOLVAS E, LY A,Synthesis and characterization of an alumina forming nanolaminated boride: MoAlB., 2016, 6: 26475.

[8] LI NING, BAI YUELEI, WANG SHUAI,Rapid synthesis, electrical, and mechanical properties of polycrystalline Fe2AlB2bulk from elemental powders., 2017, 100(10): 4407–4411.

[9] KADAS K, IUSAN D, HELLSVIK J,AlM2B2(M=Cr, Mn, Fe, Co, Ni): a group of nanolaminated materials., 2017, 29(15): 155402.

[10] ZHOU YANCHUN, XIANG HUIMIN, DAI FUZHI,Electrical conductive and damage-tolerant nanolaminated MAB phases Cr2AlB2, Cr3AlB4and Cr4AlB6., 2017, 5(6): 1–9.

[11] DAI FUZHI, FENG ZHIHAI, ZHOU YANCHUN. Easily tiltable B Al B linear chain: the origin of unusual mechanical properties of nanolaminated MAB phases (CrB2)CrAl., 2017, 723: 462–466.

[12] CHABAN N F, KUZ'MA YU B. Cheminform abstract: Ternaere systeme Cr-Al-B und Mn-Al-B., 1974, DOI: 10.1002/chin.197404029.

[13] ZHANG HAIMING, DAI FU-ZHI, XIANG HUIMIN,Crystal structure of Cr4AlB4: a new MAB phase compound discovered in Cr-Al-B system., 2019, 35(4): 530–534.

[14] DAI FUZHI, ZHANG HAIMING, XIANG HUIMIN,Theoretical investigation on the stability, mechanical and thermal properties of the newly discovered MAB phase Cr4AlB4., 2019, DOI: 10.1016/j.jmst.2019.01.017.

[15] LIU BIN, LIU YUCHEN, ZHU CHANGHUA,Advances on strategies for searching for next generation thermal barrier coating materials., 2019, 35(5): 833–851.

[16] LIU YUCHEN, COOPER VALENTINO R, WANG BANGHUI,Discovery of ABO3perovskites as thermal barrier coatings through high-throughput first principles calculations., 2019, 7(4): 145–151.

[17] KRESSE G, FURTHMÜLLER J. Efficient iterative schemes fortotal-energy calculations using a plane-wave basis set., 1996, 54(16): 11169–11186.

[18] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple., 1996, 77(18): 3865–3868.

[19] HAMMER B, HANSEN L B, NORSKOV J K. Improved adsorption energetics within density-functional theory using revised Perdew- Burke-Ernzerhof functionals., 1999, 59(11): 7413–7421.

[20] PERDEW JOHN P, CHEVARY J A, VOSKO S H,Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation., 1992, 46(11): 6671–6687.

[21] DAHLQVIST M, ALLING B, ROSÉN J. Stability trends of MAX phases from first principles., 2010, 81(22): 220102.

[22] BAI YUELEI, HE XIAODONG, SUN YUE,Chemical bonding and elastic properties of Ti3AC2phases (A=Si, Ge, and Sn): a first-principle study., 2010, 12(7): 1220–1225.

[23] SUN ZHIMEI, LI SA, AHUJA RAJEEV,Calculated elastic properties of M2AlC (M=Ti, V, Cr, Nb and Ta)., 2004, 129(9): 589–592.

[24] ANDERSON ORSON L. A simplified method for calculating the debye temperature from elastic constants., 1963, 24(7): 909–917.

[25] BAI YUELEI, QI XINXIN, DUFF ANDREW,Density functional theory insights into ternary layered boride MoAlB., 2017, 132: 69–81.

[26] BAI YUELEI, QI XINXIN, HE XIAODONG,Phase stability and weak metallic bonding within ternary-layered borides CrAlB, Cr2AlB2,Cr3AlB4, and Cr4AlB6., 2019, 102(6): 3715–3727.

[27] CHONG XIAOYU, JIANG YEHUA, ZHOU RONG,Elastic properties and electronic structures of CrBas superhard compounds., 2014, 610: 684–694.

[28] ONODERA A, HIRANO H, YUASA T,Static compression of Ti3SiC2to 61 GPa., 1999, 74(25): 3782–3784.

[29] WANG JIEMIN, ZHOU YANCHUN.investigation of the electronic structure and bonding properties of the layered ternary compound Ti3SiC2at high pressure., 2003, 15(12): 1983–1991.

[30] FRANCIS BIRCH. Finite elastic strain of cubic crystals., 1947, 71(11): 809–824.

[31] BARSOUM W MICHEL. Mechanical Properties: Ambient Temperature. MAX Phases: Properties of Machinable Ternary Carbides and Nitrides. Weinheim: Wiley, 2013.

[32] BAI YUELEI, DUFF ANDREW, JAYASEELAN DANIEL DONI,DFT predictions of crystal structure, electronic structure, compressibility, and elastic properties of Hf-Al-C carbides., 2016, 99(10): 3449–3457.

[33] BAI YUELEI, HE XIAODONG, WANG RONGGUO,Anstudy on compressibility of Al-containing MAX-phase carbides., 2013, 114(17): 173709.

[34] WANG CHANGYING, HAN HAN, ZHAO YUANYUAN,Elastic, mechanical, electronic, and defective properties of Zr-Al-C nanolaminates from first principles., 2018, 101(2): 756–772.

[35] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals., 2009, 45(367): 823–843.

Analysis on Phase Stability and Mechanical Property of Newly-discovered Ternary Layered Boride Cr4AlB4

QI Xin-Xin1, SONG Guang-Ping1, YIN Wei-Long1, WANG Ming-Fu2, HE Xiao-Dong1, ZHENG Yong-Ting1, WANG Rong-Guo1, BAI Yue-Lei1

(1. National Key Laboratory of Science and Technology on Advanced Composites in Special Environments, Harbin Institute of Technology, Harbin 150080, China; 2. Beijing Power Machinery Research Institute, Beijing 100074, China)

As newly-discovered member of the MAB phases, Cr4AlB4has much potential for high-temperature structural applications due to possible formation of a protective oxide scale. By use of “linear optimization procedure” and theoretical model of “bond stiffness” based on first-principle calculations, the phase stability and mechanical behavior of Cr4AlB4were investigated. No imaginary frequencies in phonon dispersion indicate the intrinsic stability. The lower energy as compared with the set of other competing phases also shows the thermodynamic stability. Based on the quantificationally calculated bond stiffness by use of the model of “bond stiffness”, strong covalent bonding is present between Cr and B atoms as well as B and B atoms, while the Cr-Al (625 GPa) and B-Al (574 GPa) bond is relatively weak. It follows that Cr4AlB4can be described as layered structure of strong covalently bonded Cr-B blocks interleaved by Al atomic planes where the bonding is relatively weak, similar to the well-known MAX phases, which demonstrates the similar damage tolerance and fracture toughness of Cr4AlB4with the MAX phases.

MAB phases; density functional theory; phase stability; mechanical property

TQ134

A

1000-324X(2020)01-0053-08

10.15541/jim20190160

2019-04-17;

2019-05-14

国家自然科学基金(51972080); 黑龙江省自然科学基金重点项目(ZD2017011); 中国博士后科学基金(2017T100230)

National Natural Science Foundation of China (51972080); Natural Science Foundation of Heilongjiang Province of China (ZD2017011); China Postdoctoral Science Foundation (2017T100230)

齐欣欣(1995–), 博士研究生. E-mail: 16S118138@stu.hit.edu.cn

QI Xin-Xin(1995–), PhD candidate. E-mail: 16S118138@stu.hit.edu.cn

柏跃磊, 副教授. E-mail: baiyl@hit.edu.cn

BAI Yue-Lei, associate professor. E-mail: baiyl@hit.edu.cn